Circuits numériques - Méthode K-Map
Dans les chapitres précédents, nous avons simplifié les fonctions booléennes en utilisant des postulats et théorèmes booléens. C'est un processus qui prend du temps et nous devons réécrire les expressions simplifiées après chaque étape.
Pour surmonter cette difficulté, Karnaughintroduit une méthode de simplification des fonctions booléennes de manière simple. Cette méthode est connue sous le nom de méthode de carte de Karnaugh ou méthode de K-map. C'est une méthode graphique, qui se compose de 2 n cellules pour «n» variables. Les cellules adjacentes ne diffèrent que par une position de bit unique.
K-Maps pour 2 à 5 variables
La méthode K-Map est la plus appropriée pour minimiser les fonctions booléennes de 2 variables à 5 variables. Maintenant, parlons des K-Maps pour 2 à 5 variables une par une.
2 K-Map variables
Le nombre de cellules dans 2 variables K-map est de quatre, puisque le nombre de variables est de deux. La figure suivante montre2 variable K-Map.
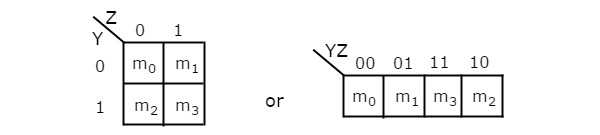
Il n'y a qu'une seule possibilité de regrouper 4 termes min adjacents.
Les combinaisons possibles de groupement de 2 termes min adjacents sont {(m 0 , m 1 ), (m 2 , m 3 ), (m 0 , m 2 ) et (m 1 , m 3 )}.
3 K-Map variables
Le nombre de cellules dans 3 variables K-map est de huit, puisque le nombre de variables est de trois. La figure suivante montre3 variable K-Map.
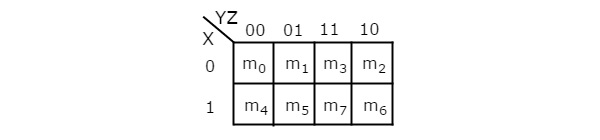
Il n'y a qu'une seule possibilité de regrouper 8 termes min adjacents.
Les combinaisons possibles de regroupement de 4 termes min adjacents sont {(m 0 , m 1 , m 3 , m 2 ), (m 4 , m 5 , m 7 , m 6 ), (m 0 , m 1 , m 4 , m 5 ), (m 1 , m 3 , m 5 , m 7 ), (m 3 , m 2 , m 7 , m 6 ) et (m 2 , m 0 , m 6 , m 4 )}.
Les combinaisons possibles de regroupement de 2 termes min adjacents sont {(m 0 , m 1 ), (m 1 , m 3 ), (m 3 , m 2 ), (m 2 , m 0 ), (m 4 , m 5 ) , (m 5 , m 7 ), (m 7 , m 6 ), (m 6 , m 4 ), (m 0 , m 4 ), (m 1 , m 5 ), (m 3 , m 7 ) et ( m 2 , m 6 )}.
Si x = 0, alors 3 variables K-map deviennent 2 variables K-map.
4 K-Map variables
Le nombre de cellules dans 4 variables K-map est de seize, puisque le nombre de variables est de quatre. La figure suivante montre4 variable K-Map.
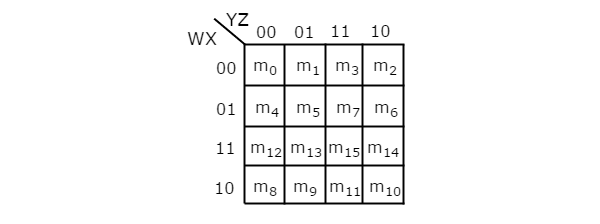
Il n'y a qu'une seule possibilité de regrouper 16 termes min adjacents.
Soit R 1 , R 2 , R 3 et R 4 les termes minimum de la première ligne, de la deuxième ligne, de la troisième ligne et de la quatrième ligne respectivement. De même, C 1 , C 2 , C 3 et C 4 représentent les termes minimum de la première colonne, deuxième colonne, troisième colonne et quatrième colonne respectivement. Les combinaisons possibles de regroupement de 8 termes min adjacents sont {(R 1 , R 2 ), (R 2 , R 3 ), (R 3 , R 4 ), (R 4 , R 1 ), (C 1 , C 2 ) , (C 2 , C 3 ), (C 3 , C 4 ), (C 4 , C 1 )}.
Si w = 0, alors 4 variables K-map deviennent 3 variables K-map.
5 K-Map variables
Le nombre de cellules dans 5 variables K-map est de trente-deux, puisque le nombre de variables est de 5. La figure suivante montre 5 variable K-Map.

Il n'y a qu'une seule possibilité de regrouper 32 termes min adjacents.
Il existe deux possibilités de regrouper 16 termes min adjacents. c'est-à-dire regroupement de termes min de m 0 à m 15 et m 16 à m 31 .
Si v = 0, alors 5 variables K-map deviennent 4 variables K-map.
Dans les K-maps ci-dessus, nous avons utilisé exclusivement la notation des termes min. De même, vous pouvez utiliser exclusivement la notation des termes Max.
Minimisation des fonctions booléennes à l'aide de K-Maps
Si nous considérons la combinaison d'entrées pour lesquelles la fonction booléenne est '1', alors nous obtiendrons la fonction booléenne, qui est dans standard sum of products forme après avoir simplifié la K-map.
De même, si nous considérons la combinaison d'entrées pour lesquelles la fonction booléenne est '0', alors nous obtiendrons la fonction booléenne, qui est dans standard product of sums forme après avoir simplifié la K-map.
Suivez ces rules for simplifying K-maps afin d'obtenir la somme standard des produits sous forme.
Sélectionnez la K-map respective en fonction du nombre de variables présentes dans la fonction booléenne.
Si la fonction booléenne est donnée sous forme de somme de termes minimum, placez les uns aux cellules de terme minimum respectives dans la K-map. Si la fonction booléenne est donnée sous forme de somme de produits, placez celles-ci dans toutes les cellules possibles de K-map pour lesquelles les termes de produit donnés sont valides.
Vérifiez les possibilités de regrouper le nombre maximum de celles adjacentes. Ce devrait être des pouvoirs de deux. Commencez par la puissance la plus élevée de deux et jusqu'à la plus petite puissance de deux. La puissance la plus élevée est égale au nombre de variables considérées dans K-map et la puissance la plus faible est égale à zéro.
Chaque groupement donnera soit un terme littéral, soit un terme de produit. Il est connu commeprime implicant. On dit que l'impliquant principal estessential prime implicant, si au moins le «1» unique n'est couvert par aucun autre groupement, mais seulement ce groupement couvre.
Notez tous les implicants principaux et les implicants principaux essentiels. La fonction booléenne simplifiée contient tous les implicants principaux essentiels et uniquement les implicants principaux requis.
Note 1 - Si les sorties ne sont pas définies pour une combinaison d'entrées, ces valeurs de sortie seront représentées par don’t care symbol ‘x’. Cela signifie que nous pouvons les considérer comme «0» ou «1».
Note 2- Si les termes indifférents sont également présents, alors placez "x" indifférent dans les cellules respectives de la K-map. Considérez uniquement les «x» indifférents qui sont utiles pour regrouper le nombre maximal de ceux adjacents. Dans ces cas, traitez la valeur Don't Care comme «1».
Exemple
Laissez-nous simplify la fonction booléenne suivante, f(W, X, Y, Z)= WX’Y’ + WY + W’YZ’ en utilisant K-map.
La fonction booléenne donnée est sous forme de somme de produits. Il a 4 variables W, X, Y & Z. Donc, nous avons besoin4 variable K-map. le4 variable K-map avec ceux correspondant aux termes du produit donnés est montré dans la figure suivante.
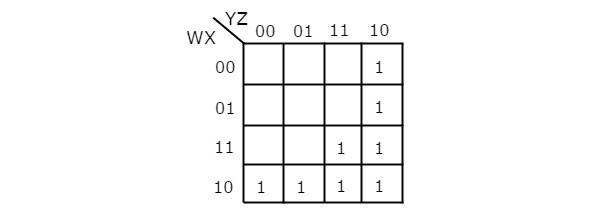
Ici, les 1 sont placés dans les cellules suivantes de la K-map.
Les cellules, communes à l'intersection de la ligne 4 et des colonnes 1 et 2 correspondent au terme produit, WX’Y’.
Les cellules, qui sont communes à l'intersection des lignes 3 et 4 et des colonnes 3 et 4 correspondent au terme produit, WY.
Les cellules communes à l'intersection des rangées 1 et 2 et de la colonne 4 correspondent au terme produit, W’YZ’.
Il n'y a aucune possibilité de regrouper 16 adjacents ou 8 adjacents. Il existe trois possibilités de regrouper 4 adjacentes. Après ces trois regroupements, il n'y en a plus un seul comme non groupé. Donc, nous n'avons pas besoin de vérifier le regroupement de 2 adjacents. le4 variable K-map avec ces trois groupings est illustré dans la figure suivante.

Ici, nous avons trois implicants principaux WX ', WY & YZ'. Tous ces principaux implicants sontessential pour les raisons suivantes.
Deux (m8 & m9)du groupe de quatrième rangée ne sont couverts par aucun autre regroupement. Seul le groupement de la quatrième rangée couvre ces deux éléments.
Un seul (m15)du groupement de forme carrée n'est couvert par aucun autre groupement. Seul le groupement de forme carrée couvre celui-là.
Deux (m2 & m6)du groupe de la quatrième colonne ne sont couverts par aucun autre groupe. Seul le groupement de la quatrième colonne couvre ces deux.
Par conséquent, la simplified Boolean function est
f = WX’ + WY + YZ’
Suivez ces rules for simplifying K-maps afin d'obtenir un produit standard sous forme de sommes.
Sélectionnez la K-map respective en fonction du nombre de variables présentes dans la fonction booléenne.
Si la fonction booléenne est donnée en tant que produit de la forme des termes Max, placez les zéros aux cellules des termes Max respectives dans la K-map. Si la fonction booléenne est donnée en tant que produit de la forme des sommes, placez les zéros dans toutes les cellules possibles de K-map pour lesquelles les termes de somme donnés sont valides.
Vérifiez les possibilités de regrouper le nombre maximum de zéros adjacents. Ce devrait être des pouvoirs de deux. Commencez par la puissance la plus élevée de deux et jusqu'à la plus petite puissance de deux. La puissance la plus élevée est égale au nombre de variables considérées dans K-map et la puissance la plus faible est égale à zéro.
Chaque groupement donnera soit un terme littéral, soit un terme de somme. Il est connu commeprime implicant. On dit que l'impliquant principal estessential prime implicant, si au moins le «0» unique n'est couvert par aucun autre groupement mais seulement ce groupement couvre.
Notez tous les implicants principaux et les implicants principaux essentiels. La fonction booléenne simplifiée contient tous les implicants principaux essentiels et uniquement les implicants principaux requis.
Note- Si les termes indifférents sont également présents, alors placez "x" indifférent dans les cellules respectives de la K-map. Considérez uniquement les «x» indifférents qui sont utiles pour regrouper le nombre maximum de zéros adjacents. Dans ces cas, traitez la valeur indifférente comme «0».
Exemple
Laissez-nous simplify la fonction booléenne suivante, $ f \ left (X, Y, Z \ right) = \ prod M \ left (0,1,2,4 \ right) $ en utilisant K-map.
La fonction booléenne donnée est le produit de la forme Max termes. Il a 3 variables X, Y et Z. Donc, nous avons besoin de 3 variables K-map. Les termes Max donnés sont M 0 , M 1 , M 2 et M 4 . Le 3variable K-map avec des zéros correspondant aux termes Max donnés est montré dans la figure suivante.

Il n'y a pas de possibilité de regrouper 8 zéros adjacents ou 4 zéros adjacents. Il existe trois possibilités de regrouper 2 zéros adjacents. Après ces trois regroupements, il n'y a plus de zéro unique non groupé. le3 variable K-map avec ces trois groupings est illustré dans la figure suivante.

Ici, nous avons trois implicants premiers X + Y, Y + Z et Z + X. Tous ces implicants premiers sont essential car un zéro dans chaque groupement n'est couvert par aucun autre groupement, sauf avec leurs groupements individuels.
Par conséquent, la simplified Boolean function est
f = (X + Y).(Y + Z).(Z + X)
De cette façon, nous pouvons facilement simplifier les fonctions booléennes jusqu'à 5 variables en utilisant la méthode K-map. Pour plus de 5 variables, il est difficile de simplifier les fonctions à l'aide de K-Maps. Parce que, le nombre decells dans K-map obtient doubled en incluant une nouvelle variable.
En raison de cette vérification et le regroupement de ceux adjacents (termes minimum) ou de zéros adjacents (termes maximum) sera compliqué. Nous discuteronsTabular method dans le prochain chapitre pour surmonter les difficultés de la méthode K-map.