Circuits numériques - Logique de seuil
Dans les chapitres précédents, nous avons implémenté divers circuits combinatoires utilisant des portes logiques. À l'exception de la porte NOT, toutes les portes logiques restantes ont au moins deux entrées et une seule sortie. De même, lethreshold gate contient également au moins une entrée et une seule sortie.
De plus, il contient les poids respectifs de chaque entrée et une valeur de seuil. Les valeurs de ces poids et seuils pourraient être de n'importe quel nombre réel fini.
Principes de base de la porte de seuil
Soit les entrées de la porte de seuil sont X 1 , X 2 , X 3 ,…, X n . Les poids correspondants de ces entrées sont W 1 , W 2 , W 3 ,…, W n . lesymbol de seuil de seuil est illustré dans la figure suivante.
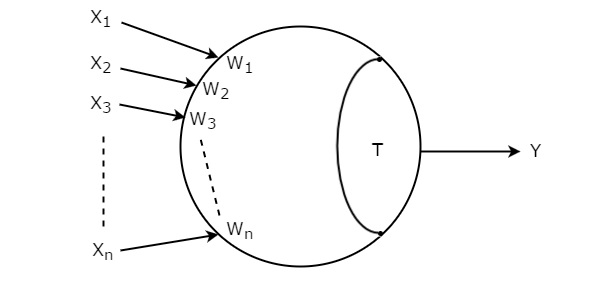
Threshold gateest représenté par un cercle et il a «n» entrées, X 1 à X n et une seule sortie, Y. Ce cercle est composé de deux parties. Une partie représente les poids correspondant aux entrées et l'autre partie représente la valeur de seuil, T.
La somme des produits des intrants avec les poids correspondants est appelée weighted sum. Si cette somme pondérée est supérieure ou égale à la valeur de seuil, T alors seule la sortie, Y sera égale à un. Sinon, la sortie, Y sera égale à zéro.
Mathematically, nous pouvons écrire cette relation entre les entrées et la sortie de la porte de seuil comme ci-dessous.
$$ Y = 1, si \: \: W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} + ... W_ {n} X_ {n} \ geq T $$
= 0, sinon.
Par conséquent, nous pouvons implémenter diverses portes logiques et fonctions booléennes simplement en modifiant les valeurs des poids et / ou la valeur de seuil, T.
Exemple
Trouvons le simplified Boolean function pour la porte de seuil suivante.

Cette porte de seuil a trois entrées X 1 , X 2 , X 3 et une sortie Y.
Les poids correspondant aux entrées X 1 , X 2 et X 3 sont respectivement W 1 = 2, W 2 = 1 & W 3 = -4.
La valeur de la porte de seuil est T = -1.
le weighted sum de la porte de seuil est
$$ W = W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} $$
Remplacez les poids donnés dans l'équation ci-dessus.
$$ \ Rightarrow W = 2X_ {1} + X_ {2} -4X_ {3} $$
Sortie de la porte de seuil, Y sera «1» si W ≥ −1, sinon ce sera «0».
Le suivant table montre la relation entre l'entrée et la sortie pour toutes les combinaisons possibles d'entrées.
| Contributions | Somme pondérée | Production | ||
|---|---|---|---|---|
| $ X_ {1} $ | $ X_ {2} $ | $ X_ {3} $ | $ W = 2X_ {1} + X_ {2} -4X_ {3} $ | $ Y $ |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | -4 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | -3 | 0 |
| 1 | 0 | 0 | 2 | 1 |
| 1 | 0 | 1 | -2 | 0 |
| 1 | 1 | 0 | 3 | 1 |
| 1 | 1 | 1 | -1 | 1 |
À partir du tableau ci-dessus, nous pouvons écrire le Boolean function pour la sortie, Y comme
$$ Y = \ somme m \ gauche (0,2,4,6,7 \ droite) $$
La simplification de cette fonction booléenne en utilisant 3 variable K-Map est illustré dans la figure suivante.

Par conséquent, la simplified Boolean function pour un seuil donné, la porte est $ Y = {X_ {3} '} + X_ {1} X_ {2} $.
Synthèse des fonctions de seuil
La porte de seuil est également appelée universal gatecar nous pouvons implémenter n'importe quelle fonction booléenne en utilisant la ou les portes de seuil. Parfois, il peut ne pas être possible d'implémenter quelques portes logiques et fonctions booléennes en utilisant une seule porte de seuil. Dans ce cas, nous pouvons avoir besoin de plusieurs portes de seuil.
Suivez ces steps pour implémenter une fonction booléenne en utilisant une seule porte de seuil.
Step 1 - Formuler un Truth table pour une fonction booléenne donnée.
Step 2 - Dans le tableau de vérité ci-dessus, ajoutez (incluez) une colonne supplémentaire, qui donne la relation entre weighted sums et Threshold value.
Step 3 - Écrivez la relation entre les sommes pondérées et le seuil pour chaque combinaison d'entrées comme indiqué ci-dessous.
Si la sortie de la fonction booléenne est 1, alors la somme pondérée sera supérieure ou égale à la valeur de seuil pour ces combinaisons d'entrées.
Si la sortie de la fonction booléenne est 0, alors la somme pondérée sera inférieure à la valeur de seuil pour ces combinaisons d'entrées.
Step 4 - Choisissez les valeurs de poids et de seuil de manière à ce qu'elles satisfassent toutes les relations présentes dans la dernière colonne du tableau ci-dessus.
step 5 - Dessinez le symbol de la porte de seuil avec ces poids et la valeur de seuil.
Exemple
Laissez-nous mettre en œuvre ce qui suit Boolean function en utilisant une seule porte de seuil.
$$ Y \ left (X_ {1}, X_ {2}, X_ {3} \ right) = \ somme m \ left (0,2,4,6,7 \ right) $$
La fonction booléenne donnée est une fonction à trois variables, qui est représentée sous forme de somme de termes min. leTruth table de cette fonction est illustrée ci-dessous.
| Contributions | Production | ||
|---|---|---|---|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Maintenant, ajoutons (incluons) une colonne supplémentaire au tableau de vérité ci-dessus. Cette dernière colonne contient les relations entreweighted sums (W) and Threshold valeur (T) pour chaque combinaison d'entrées.
| Contributions | Production | Relations entre W & T | ||
|---|---|---|---|---|
| X1 | X2 | X3 | Y | |
| 0 | 0 | 0 | 1 | 0 ≥T |
| 0 | 0 | 1 | 0 | W 3 <T |
| 0 | 1 | 0 | 1 | W 2 ≥ T |
| 0 | 1 | 1 | 0 | W 2 + W 3 <T |
| 1 | 0 | 0 | 1 | W 1 ≥ T |
| 1 | 0 | 1 | 0 | W 1 + W 3 <T |
| 1 | 1 | 0 | 1 | W 1 + W 2 ≥ T |
| 1 | 1 | 1 | 1 | W 1 + W 2 + W 3 ≥ T |
Voici les conclusions du tableau ci-dessus.
La valeur du seuil doit être nulle ou négative en fonction de la première relation.
La valeur de W 3 doit être négative en fonction des première et seconde relations.
Les valeurs de W 1 et W 2 doivent être supérieures ou égales à la valeur de seuil basée sur les cinquième et troisième relations.
W 2 doit être supérieur à W 3 sur la base de la quatrième relation.
Nous pouvons choisir les valeurs suivantes pour les poids et le seuil en fonction des conclusions ci-dessus.
W 1 = 2, W 2 = 1, W 3 = -4 et T = -1
le symbol du seuil de seuil avec les valeurs ci-dessus est indiqué ci-dessous.

Par conséquent, cette porte de seuil implémente le Boolean function, $ Y \ left (X_ {1}, X_ {2}, X_ {3} \ right) = \ somme m \ left (0,2,4,6,7 \ right) $.