Circuits numériques - Guide rapide
Si la base ou la base d'un système numérique est «r», alors les nombres présents dans ce système numérique vont de zéro à r-1. Le nombre total présent dans ce système numérique est «r». Ainsi, nous obtiendrons divers systèmes de nombres, en choisissant les valeurs de base comme supérieures ou égales à deux.
Dans ce chapitre, parlons de la popular number systemset comment représenter un nombre dans le système numérique respectif. Les systèmes numériques suivants sont les plus couramment utilisés.
- Système de nombres décimaux
- Système de numération binaire
- Système de nombre octal
- Système de nombres hexadécimaux
Système de nombres décimaux
le base ou la base du système de nombres décimaux est 10. Ainsi, les nombres allant de 0 à 9 sont utilisés dans ce système numérique. La partie du nombre qui se trouve à gauche dudecimal pointest appelée partie entière. De même, la partie du nombre située à droite de la virgule décimale est appelée partie fractionnaire.
Dans ce système numérique, les positions successives à gauche du point décimal ont des poids de 10 0 , 10 1 , 10 2 , 10 3 et ainsi de suite. De même, les positions successives à droite du point décimal ont des poids de 10 -1 , 10 -2 , 10 -3 et ainsi de suite. Cela signifie que chaque position a un poids spécifique, qui estpower of base 10
Exemple
Prendre en compte decimal number 1358.246. La partie entière de ce nombre est 1358 et la partie fractionnaire de ce nombre est 0,246. Les chiffres 8, 5, 3 et 1 ont des poids de 100, 101, 10 2 et 10 3 respectivement. De même, les chiffres 2, 4 et 6 ont des poids de 10 -1 , 10 -2 et 10 -3 respectivement.
Mathematically, nous pouvons l'écrire comme
1358.246 = (1 × 10 3 ) + (3 × 10 2 ) + (5 × 10 1 ) + (8 × 10 0 ) + (2 × 10 -1 ) +
(4 × 10 -2 ) + (6 × 10 -3 )
Après avoir simplifié les termes de droite, nous obtiendrons le nombre décimal, qui se trouve sur le côté gauche.
Système de numération binaire
Tous les circuits et systèmes numériques utilisent ce système de nombres binaires. lebase ou la base de ce système numérique est 2. Ainsi, les nombres 0 et 1 sont utilisés dans ce système numérique.
La partie du nombre qui se trouve à gauche du binary pointest appelée partie entière. De même, la partie du nombre située à droite du point binaire est appelée partie fractionnaire.
Dans ce système numérique, les positions successives à gauche du point binaire ont des poids de 2 0 , 2 1 , 2 2 , 2 3 et ainsi de suite. De même, les positions successives à droite du point binaire ont des poids de 2 -1 , 2 -2 , 2 -3 et ainsi de suite. Cela signifie que chaque position a un poids spécifique, qui estpower of base 2.
Exemple
Prendre en compte binary number 1101.011. La partie entière de ce nombre est 1101 et la partie fractionnaire de ce nombre est 0,011. Les chiffres 1, 0, 1 et 1 de la partie entière ont des poids de 2 0 , 2 1 , 2 2 , 2 3 respectivement. De même, les chiffres 0, 1 et 1 de la partie fractionnaire ont des poids de 2 -1 , 2 -2 , 2 -3 respectivement.
Mathematically, nous pouvons l'écrire comme
1101.011 = (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) + (0 × 2 -1 ) +
(1 × 2 -2 ) + (1 × 2 -3 )
Après avoir simplifié les termes de droite, nous obtiendrons un nombre décimal, qui est un équivalent du nombre binaire sur le côté gauche.
Système de nombre octal
le base ou la base du système de nombres octaux est 8. Ainsi, les nombres allant de 0 à 7 sont utilisés dans ce système numérique. La partie du nombre qui se trouve à gauche duoctal pointest appelée partie entière. De même, la partie du nombre située à droite du point octal est appelée partie fractionnaire.
Dans ce système numérique, les positions successives à gauche du point octal ont des poids de 8 0 , 8 1 , 8 2 , 8 3 et ainsi de suite. De même, les positions successives à droite du point octal ont des poids de 8 -1 , 8 -2 , 8 -3 et ainsi de suite. Cela signifie que chaque position a un poids spécifique, qui estpower of base 8.
Exemple
Prendre en compte octal number 1457.236. La partie entière de ce nombre est 1457 et la partie fractionnaire de ce nombre est 0,236. Les chiffres 7, 5, 4 et 1 ont des poids de 8 0 , 8 1 , 8 2 et 8 3 respectivement. De même, les chiffres 2, 3 et 6 ont des poids de 8 -1 , 8 -2 , 8 -3 respectivement.
Mathematically, nous pouvons l'écrire comme
1457.236 = (1 × 8 3 ) + (4 × 8 2 ) + (5 × 8 1 ) + (7 × 8 0 ) + (2 × 8 -1 ) +
(3 × 8 -2 ) + (6 × 8-3 )
Après avoir simplifié les termes de droite, nous obtiendrons un nombre décimal, qui est un équivalent du nombre octal sur le côté gauche.
Système de nombres hexadécimaux
le base ou la base du système de nombres hexadécimaux est 16. Ainsi, les nombres allant de 0 à 9 et les lettres de A à F sont utilisés dans ce système numérique. L'équivalent décimal des chiffres hexadécimaux de A à F va de 10 à 15.
La partie du nombre qui se trouve à gauche du hexadecimal pointest appelée partie entière. De même, la partie du nombre située à droite de la virgule hexadécimale est appelée partie fractionnaire.
Dans ce système numérique, les positions successives à gauche du point hexadécimal ont des poids de 16 0 , 16 1 , 16 2 , 16 3 et ainsi de suite. De même, les positions successives à droite du point hexadécimal ont des poids de 16 -1 , 16 -2 , 16 -3 et ainsi de suite. Cela signifie que chaque position a un poids spécifique, qui estpower of base 16.
Exemple
Prendre en compte Hexa-decimal number 1A05.2C4. La partie entière de ce nombre est 1A05 et la partie fractionnaire de ce nombre est 0.2C4. Les chiffres 5, 0, A et 1 ont des poids de 16 0 , 16 1 , 16 2 et 16 3 respectivement. De même, les chiffres 2, C et 4 ont des poids de 16 -1 , 16 -2 et 16 -3 respectivement.
Mathematically, nous pouvons l'écrire comme
1A05.2C4 = (1 × 16 3 ) + (10 × 16 2 ) + (0 × 16 1 ) + (5 × 16 0 ) + (2 × 16 -1 ) +
(12 × 16 -2 ) + (4 × 16-3 )
Après avoir simplifié les termes du côté droit, nous obtiendrons un nombre décimal, qui est un équivalent du nombre hexadécimal sur le côté gauche.
Dans le chapitre précédent, nous avons vu les quatre systèmes numériques importants. Dans ce chapitre, convertissons les nombres d'un système numérique à l'autre afin de trouver la valeur équivalente.
Conversion de nombres décimaux en autres bases
Si le nombre décimal contient à la fois une partie entière et une partie fractionnaire, convertissez les deux parties du nombre décimal en une autre base individuellement. Suivez ces étapes pour convertir le nombre décimal en son nombre équivalent de n'importe quelle base «r».
Faire division de la partie entière du nombre décimal et successive quotientsavec la base 'r' et notez les restes jusqu'à ce que le quotient soit zéro. Considérez les restes dans l'ordre inverse pour obtenir la partie entière du nombre équivalent de base «r». Cela signifie que le premier et le dernier reste désignent respectivement le chiffre le moins significatif et le chiffre le plus significatif.
Faire multiplication de partie fractionnaire du nombre décimal et successive fractionsavec la base «r» et notez le report jusqu'à ce que le résultat soit zéro ou que le nombre souhaité de chiffres équivalents soit obtenu. Considérez la séquence normale de report afin d'obtenir la partie fractionnaire du nombre équivalent de base «r».
Conversion décimale en binaire
Les deux types d'opérations suivants ont lieu lors de la conversion d'un nombre décimal en son nombre binaire équivalent.
- Division de la partie entière et des quotients successifs avec la base 2.
- Multiplication de la partie fractionnaire et des fractions successives avec la base 2.
Example
Prendre en compte decimal number 58.25. Ici, la partie entière est 58 et la partie fractionnaire est 0,25.
Step 1 - Division de 58 et quotients successifs en base 2.
| Opération | Quotient | Reste |
|---|---|---|
| 58/2 | 29 | 0 (LSB) |
| 29/2 | 14 | 1 |
| 14/2 | sept | 0 |
| 7/2 | 3 | 1 |
| 3/2 | 1 | 1 |
| 1/2 | 0 | 1(MSB) |
⇒ (58) 10 = (111010) 2
Par conséquent, la integer part de nombre binaire équivalent est 111010.
Step 2 - Multiplication de 0,25 et fractions successives en base 2.
| Opération | Résultat | Porter |
|---|---|---|
| 0,25 x 2 | 0,5 | 0 |
| 0,5 x 2 | 1.0 | 1 |
| - | 0,0 | - |
⇒ (.25) 10 = (.01) 2
Par conséquent, la fractional part de nombre binaire équivalent est .01
⇒ (58,25) 10 = (111010,01) 2
Par conséquent, la binary equivalent du nombre décimal 58.25 est 111010.01.
Conversion décimale en octale
Les deux types d'opérations suivants ont lieu lors de la conversion d'un nombre décimal en son nombre octal équivalent.
Division de la partie entière et des quotients successifs avec base 8.
Multiplication de la partie fractionnaire et des fractions successives avec la base 8.
Example
Prendre en compte decimal number 58.25. Ici, la partie entière est 58 et la partie fractionnaire est 0,25.
Step 1 - Division de 58 et quotients successifs en base 8.
| Opération | Quotient | Reste |
|---|---|---|
| 58/8 | sept | 2 |
| 7/8 | 0 | 7 |
⇒ (58) 10 = (72) 8
Par conséquent, la integer part de nombre octal équivalent est 72.
Step 2 - Multiplication de 0,25 et fractions successives en base 8.
| Opération | Résultat | Porter |
|---|---|---|
| 0,25 x 8 | 2,00 | 2 |
| - | 0,00 | - |
⇒ (.25) 10 = (.2) 8
Par conséquent, la fractional part du nombre octal équivalent est .2
⇒ (58,25) 10 = (72,2) 8
Par conséquent, la octal equivalent du nombre décimal 58,25 est 72,2.
Conversion décimale en hexa-décimale
Les deux types d'opérations suivants ont lieu lors de la conversion d'un nombre décimal en son nombre hexadécimal équivalent.
- Division de la partie entière et des quotients successifs en base 16.
- Multiplication de la partie fractionnaire et des fractions successives en base 16.
Example
Prendre en compte decimal number 58.25. Ici, la partie entière est 58 et la partie décimale est 0,25.
Step 1 - Division de 58 et quotients successifs en base 16.
| Opération | Quotient | Reste |
|---|---|---|
| 58/16 | 3 | 10 = A |
| 3/16 | 0 | 3 |
⇒ (58) 10 = (3A) 16
Par conséquent, la integer part du nombre hexadécimal équivalent est 3A.
Step 2 - Multiplication de 0,25 et fractions successives en base 16.
| Opération | Résultat | Porter |
|---|---|---|
| 0,25 x 16 | 4,00 | 4 |
| - | 0,00 | - |
⇒ (0,25) 10 = (0,4) 16
Par conséquent, la fractional part du nombre hexadécimal équivalent est 0,4.
⇒(58.25)10 = (3A.4)16
Par conséquent, la Hexa-decimal equivalent du nombre décimal 58,25 est 3A.4.
Conversion de nombres binaires vers d'autres bases
Le processus de conversion d'un nombre binaire en nombre décimal est différent du processus de conversion d'un nombre binaire en d'autres bases. Parlons maintenant de la conversion d'un nombre binaire en systèmes de nombres décimaux, octaux et hexadécimaux un par un.
Conversion binaire en décimale
Pour convertir un nombre binaire en son nombre décimal équivalent, multipliez d'abord les bits du nombre binaire par les poids positionnels respectifs, puis ajoutez tous ces produits.
Example
Prendre en compte binary number 1101.11.
Mathematically, nous pouvons l'écrire comme
(1101.11) 2 = (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) + (1 × 2 -1 ) +
(1 × 2 -2 )
⇒ (1101,11) 2 = 8 + 4 + 0 + 1 + 0,5 + 0,25 = 13,75
⇒ (1101,11) 2 = (13,75) 10
Par conséquent, la decimal equivalent du nombre binaire 1101.11 est 13.75.
Conversion binaire en octale
Nous savons que les bases des systèmes de nombres binaires et octaux sont respectivement 2 et 8. Trois bits de nombre binaire équivalent à un chiffre octal, puisque 2 3 = 8.
Suivez ces deux étapes pour convertir un nombre binaire en son nombre octal équivalent.
Partir du point binaire et former les groupes de 3 bits de part et d'autre du point binaire. Si un ou deux bits sont inférieurs lors de la création du groupe de 3 bits, alors incluez le nombre requis de zéros sur les côtés extrêmes.
Écrivez les chiffres octaux correspondant à chaque groupe de 3 bits.
Example
Prendre en compte binary number 101110.01101.
Step 1 - Faites les groupes de 3 bits de part et d'autre du point binaire.
101110.011 01
Ici, à droite du point binaire, le dernier groupe n'a que 2 bits. Donc, incluez un zéro sur le côté extrême afin de le rendre comme un groupe de 3 bits.
⇒ 101110,011 010
Step 2 - Ecrivez les chiffres octaux correspondant à chaque groupe de 3 bits.
⇒ (101110,011 010) 2 = (56,32) 8
Par conséquent, la octal equivalent du nombre binaire 101110.01101 est 56.32.
Conversion binaire en hexa-décimal
Nous savons que les bases des systèmes de nombres binaires et hexadécimaux sont respectivement 2 et 16. Quatre bits de nombre binaire équivalent à un chiffre hexadécimal, puisque 2 4 = 16.
Suivez ces deux étapes pour convertir un nombre binaire en son nombre hexadécimal équivalent.
Partir du point binaire et former les groupes de 4 bits de part et d'autre du point binaire. Si certains bits sont inférieurs lors de la création du groupe de 4 bits, alors incluez le nombre requis de zéros sur les côtés extrêmes.
Écrivez les chiffres hexadécimaux correspondant à chaque groupe de 4 bits.
Example
Prendre en compte binary number 101110.01101
Step 1 - Faites les groupes de 4 bits de part et d'autre du point binaire.
10 1110.0110 1
Ici, le premier groupe n'a que 2 bits. Donc, incluez deux zéros sur le côté extrême afin de le faire comme un groupe de 4 bits. De même, incluez trois zéros sur le côté extrême pour que le dernier groupe soit également un groupe de 4 bits.
⇒ 0010 1110.0110 1000
Step 2 - Ecrivez les chiffres hexadécimaux correspondant à chaque groupe de 4 bits.
⇒ (0010 1110,0110 1000) 2 = (2E.68) 16
Par conséquent, la Hexa-decimal equivalent du nombre binaire 101110.01101 est (2E.68).
Conversion de nombre octal vers d'autres bases
Le processus de conversion d'un nombre d'octal en nombre décimal est différent du processus de conversion d'un nombre octal en d'autres bases. Parlons maintenant de la conversion d'un nombre octal en systèmes de nombres décimaux, binaires et hexadécimaux un par un.
Conversion octale en décimale
Pour convertir un nombre octal en son nombre décimal équivalent, multipliez d'abord les chiffres du nombre octal par les poids positionnels respectifs, puis ajoutez tous ces produits.
Example
Prendre en compte octal number 145.23.
Mathematically, nous pouvons l'écrire comme
(145.23) 8 = (1 × 8 2 ) + (4 × 8 1 ) + (5 × 8 0 ) + (2 × 8 -1 ) + (3 × 8 -2 )
⇒ (145,23) 8 = 64 + 32 + 5 + 0,25 + 0,05 = 101,3
⇒ (145,23) 8 = (101,3) 10
Par conséquent, la decimal equivalent du nombre octal 145.23 est 101.3.
Conversion octale en binaire
Le processus de conversion d'un nombre octal en un nombre binaire équivalent est juste opposé à celui de la conversion binaire en octal. En représentant chaque chiffre octal avec 3 bits, nous obtiendrons le nombre binaire équivalent.
Example
Prendre en compte octal number 145.23.
Représentez chaque chiffre octal avec 3 bits.
(145,23) 8 = (001100 101,010 011) 2
La valeur ne change pas en supprimant les zéros, qui sont à l'extrême.
⇒ (145,23) 8 = (1100101,010011) 2
Par conséquent, la binary equivalent du nombre octal 145.23 est 1100101.010011.
Conversion octale en hexadécimal
Suivez ces deux étapes pour convertir un nombre octal en son nombre hexadécimal équivalent.
- Convertit le nombre octal en son nombre binaire équivalent.
- Convertissez le nombre binaire ci-dessus en son nombre hexadécimal équivalent.
Example
Prendre en compte octal number 145.23
Dans l'exemple précédent, nous avons obtenu l'équivalent binaire du nombre octal 145.23 comme 1100101.010011.
En suivant la procédure de conversion binaire en hexadécimal, nous obtiendrons
(1100101.010011) 2 = (65.4C) 16
⇒ (145,23) 8 = (65,4C) 16
Par conséquent, la Hexa-decimal equivalentdu nombre octal est 145,23 65,4 C .
Conversion de nombres hexadécimaux vers d'autres bases
Le processus de conversion d'un nombre hexadécimal en nombre décimal est différent du processus de conversion d'un nombre hexadécimal en d'autres bases. Parlons maintenant de la conversion des nombres hexadécimaux en systèmes de nombres décimaux, binaires et octaux un par un.
Conversion hexadécimale en décimale
Pour convertir un nombre hexadécimal en son nombre décimal équivalent, multipliez d'abord les chiffres du nombre hexadécimal par les poids positionnels respectifs, puis ajoutez tous ces produits.
Example
Prendre en compte Hexa-decimal number 1A5.2
Mathematically, nous pouvons l'écrire comme
(1A5.2) 16 = (1 × 16 2 ) + (10 × 16 1 ) + (5 × 16 0 ) + (2 × 16 -1 )
⇒ (1A5.2) 16 = 256 + 160 + 5 + 0,125 = 421,125
⇒ (1A5.2) 16 = (421,125) 10
Par conséquent, la decimal equivalent du nombre hexadécimal 1A5.2 est 421.125.
Conversion hexadécimale en binaire
Le processus de conversion d'un nombre hexadécimal en son nombre binaire équivalent est juste opposé à celui de la conversion binaire en hexadécimal. En représentant chaque chiffre hexadécimal avec 4 bits, nous obtiendrons le nombre binaire équivalent.
Example
Prendre en compte Hexa-decimal number 65.4C
Représentez chaque chiffre hexadécimal avec 4 bits.
(65,4C) 6 = (0110 0101.0100 1100) 2
La valeur ne change pas en supprimant les zéros, qui sont à deux côtés extrêmes.
⇒ (65,4C) 16 = (1100101,010011) 2
Par conséquent, la binary equivalent du nombre hexadécimal 65.4C est 1100101.010011.
Conversion hexadécimale en octale
Suivez ces deux étapes pour convertir un nombre hexadécimal en son nombre octal équivalent.
- Convertissez un nombre hexadécimal en son nombre binaire équivalent.
- Convertissez le nombre binaire ci-dessus en son nombre octal équivalent.
Example
Prendre en compte Hexa-decimal number 65.4C
Dans l'exemple précédent, nous avons obtenu l'équivalent binaire du nombre hexadécimal 65,4C sous la forme 1100101.010011.
En suivant la procédure de conversion binaire en octal, nous obtiendrons
(1100101.010011) 2 = (145,23) 8
⇒ (65,4C) 16 = (145,23)
Par conséquent, la octal equivalentdu nombre hexadécimal 65,4 C est 145,23.
Nous pouvons faire des nombres binaires les deux groupes suivants - Unsigned numbers et Signed numbers.
Numéros non signés
Les nombres non signés ne contiennent que la grandeur du nombre. Ils n'ont aucun signe. Cela signifie que tous les nombres binaires non signés sont positifs. Comme dans le système de nombres décimaux, le placement du signe positif devant le nombre est facultatif pour représenter des nombres positifs. Par conséquent, tous les nombres positifs, y compris zéro, peuvent être traités comme des nombres non signés si le signe positif n'est pas attribué devant le nombre.
Numéros signés
Les nombres signés contiennent à la fois le signe et la grandeur du nombre. Généralement, le signe est placé devant le numéro. Nous devons donc considérer le signe positif pour les nombres positifs et le signe négatif pour les nombres négatifs. Par conséquent, tous les nombres peuvent être traités comme des nombres signés si le signe correspondant est attribué devant le nombre.
Si le bit de signe est zéro, ce qui indique que le nombre binaire est positif. De même, si le bit de signe est un, ce qui indique que le nombre binaire est négatif.
Représentation des nombres binaires non signés
Les bits présents dans le nombre binaire non signé contiennent le magnituded'un certain nombre. Cela signifie que si le nombre binaire non signé contient‘N’ bits, puis tout N les bits représentent la grandeur du nombre, car il n'a pas de bit de signe.
Example
Prendre en compte decimal number 108. L'équivalent binaire de ce nombre est1101100. C'est la représentation d'un nombre binaire non signé.
(108) 10 = (1101100) 2
Il a 7 bits. Ces 7 bits représentent la grandeur du nombre 108.
Représentation des nombres binaires signés
Le bit le plus significatif (MSB) des nombres binaires signés est utilisé pour indiquer le signe des nombres. Par conséquent, il est également appelé commesign bit. Le signe positif est représenté en plaçant «0» dans le bit de signe. De même, le signe négatif est représenté en plaçant «1» dans le bit de signe.
Si le nombre binaire signé contient «N» bits, alors (N-1) bits ne représentent que la grandeur du nombre puisqu'un bit (MSB) est réservé pour représenter le signe du nombre.
Il ya trois types of representations pour les nombres binaires signés
- Formulaire Sign-Magnitude
- Forme du complément 1
- Forme du complément 2
La représentation d'un nombre positif dans ces 3 formes est la même. Mais, seule la représentation du nombre négatif différera dans chaque forme.
Example
Prendre en compte positive decimal number +108. L'équivalent binaire de la grandeur de ce nombre est 1101100. Ces 7 bits représentent la grandeur du nombre 108. Comme il s'agit d'un nombre positif, considérez le bit de signe comme zéro, qui est placé sur le côté le plus à gauche de la grandeur.
(+108) 10 = (01101100) 2
Par conséquent, la signed binary representationdu nombre décimal positif +108 est. Ainsi, la même représentation est valide sous forme de signe-magnitude, de complément à 1 et de complément à 2 pour un nombre décimal positif +108.
Formulaire Sign-Magnitude
Sous forme de signe-magnitude, le MSB est utilisé pour représenter sign du nombre et les bits restants représentent le magnitudedu nombre. Donc, incluez simplement le bit de signe à l'extrême gauche du nombre binaire non signé. Cette représentation est similaire à la représentation des nombres décimaux signés.
Example
Prendre en compte negative decimal number -108. La grandeur de ce nombre est de 108. Nous savons que la représentation binaire non signée de 108 est 1101100. Elle a 7 bits. Tous ces bits représentent la grandeur.
Puisque le nombre donné est négatif, considérez le bit de signe comme un, qui est placé à l'extrême gauche de la grandeur.
(−108) 10 = (11101100) 2
Par conséquent, la représentation de l'amplitude du signe de -108 est 11101100.
Forme du complément 1
Le complément 1 d'un nombre est obtenu par complementing all the bitsdu nombre binaire signé. Ainsi, le complément 1 du nombre positif donne un nombre négatif. De même, le complément d'un nombre négatif à 1 donne un nombre positif.
Cela signifie que si vous effectuez deux fois le complément de 1 d'un nombre binaire comprenant le bit de signe, vous obtiendrez le nombre binaire signé d'origine.
Example
Prendre en compte negative decimal number -108. La magnitude de ce nombre est de 108. Nous savons que la représentation binaire signée de 108 est 01101100.
Il a 8 bits. Le MSB de ce nombre est zéro, ce qui indique un nombre positif. Le complément de zéro est un et vice-versa. Donc, remplacez les zéros par des uns et les uns par des zéros afin d'obtenir le nombre négatif.
(−108) 10 = (10010011) 2
Par conséquent, la 1’s complement of (108)10 est (10010011)2.
Forme du complément 2
Le complément à 2 d'un nombre binaire est obtenu par adding one to the 1’s complementdu nombre binaire signé. Ainsi, le complément 2 du nombre positif donne un nombre négatif. De même, le complément de 2 d'un nombre négatif donne un nombre positif.
Cela signifie que si vous effectuez deux fois le complément de 2 d'un nombre binaire comprenant le bit de signe, vous obtiendrez le nombre binaire signé d'origine.
Example
Prendre en compte negative decimal number -108.
Nous connaissons le complément 1 de (108)10 est (10010011)2
2 compliment de (108) 10 = 1 compliment de (108) 10 + 1.
= 10010011 + 1
= 10010100
Par conséquent, la 2’s complement of (108)10 est (10010100)2.
Dans ce chapitre, discutons des opérations arithmétiques de base, qui peuvent être effectuées sur deux nombres binaires signés en utilisant la méthode du complément à 2. lebasic arithmetic operations sont l'addition et la soustraction.
Ajout de deux nombres binaires signés
Considérez les deux nombres binaires signés A et B, qui sont représentés sous forme de complément à 2. Nous pouvons effectuer leadditionde ces deux nombres, ce qui est similaire à l'addition de deux nombres binaires non signés. Mais, si la somme résultante contient le bit de réalisation à partir du signe, alors éliminez-le (ignorez) afin d'obtenir la valeur correcte.
Si la somme résultante est positive, vous pouvez en trouver directement l'ampleur. Mais, si la somme résultante est négative, prenez-en le complément à 2 pour obtenir la grandeur.
Exemple 1
Laissez-nous effectuer le addition de deux nombres décimaux +7 and +4 en utilisant la méthode du complément à 2.
le 2’s complement Les représentations de +7 et +4 avec 5 bits chacune sont présentées ci-dessous.
(+7) 10 = (00111) 2
(+4) 10 = (00100) 2
L'ajout de ces deux nombres est
(+7) 10 + (+ 4) 10 = (00111) 2 + (00100) 2
⇒ (+7) 10 + (+ 4) 10 = (01011) 2 .
La somme résultante contient 5 bits. Donc, il n'y a pas d'exécution à partir du bit de signe. Le bit de signe '0' indique que la somme résultante estpositive. Ainsi, la grandeur de la somme est de 11 dans le système de nombres décimaux. Par conséquent, l'addition de deux nombres positifs donnera un autre nombre positif.
Exemple 2
Laissez-nous effectuer le addition de deux nombres décimaux -7 et -4 en utilisant la méthode du complément à 2.
le 2’s complement La représentation de -7 et -4 avec 5 bits chacun est indiquée ci-dessous.
(−7) 10 = (11001) 2
(−4) 10 = (11100) 2
L'ajout de ces deux nombres est
(−7) 10 + (−4) 10 = (11001) 2 + (11100) 2
⇒ (−7) 10 + (−4) 10 = (110101) 2 .
La somme résultante contient 6 bits. Dans ce cas, la retenue est obtenue à partir du bit de signe. Donc, nous pouvons le supprimer
La somme résultante après suppression du report est (−7) 10 + (−4) 10 =(10101)2.
Le bit de signe '1' indique que la somme résultante est negative. Donc, en prenant le complément de 2, nous obtiendrons la grandeur de la somme résultante comme 11 dans le système de nombres décimaux. Par conséquent, l'addition de deux nombres négatifs donnera un autre nombre négatif.
Soustraction de deux nombres binaires signés
Considérez les deux nombres binaires signés A et B, qui sont représentés sous forme de complément à 2. Nous savons que le complément d'un nombre positif à 2 donne un nombre négatif. Donc, chaque fois que nous devons soustraire un nombre B du nombre A, alors prenez le complément 2 de B et ajoutez-le à A. Donc,mathematically nous pouvons l'écrire comme
A - B = A + (2's complement of B)
De même, si nous devons soustraire le nombre A du nombre B, alors prenez le complément à 2 de A et ajoutez-le à B. Donc, mathematically nous pouvons l'écrire comme
B - A = B + (2's complement of A)
Ainsi, la soustraction de deux nombres binaires signés est similaire à l'addition de deux nombres binaires signés. Mais, nous devons prendre le complément de 2 du nombre, qui est censé être soustrait. C'est leadvantagede la technique du complément à 2. Suivez, les mêmes règles d'addition de deux nombres binaires signés.
Exemple 3
Laissez-nous effectuer le subtraction de deux nombres décimaux +7 and +4 en utilisant la méthode du complément à 2.
La soustraction de ces deux nombres est
(+7) 10 - (+4) 10 = (+7) 10 + (−4) 10 .
le 2’s complement La représentation de +7 et -4 avec 5 bits chacun est indiquée ci-dessous.
(+7) 10 = (00111) 2
(+4) 10 = (11100) 2
⇒ (+7) 10 + (+4) 10 = (00111) 2 + (11100) 2 = (00011) 2
Ici, le report obtenu à partir du bit de signe. Donc, nous pouvons le supprimer. La somme résultante après suppression du report est
(+7) 10 + (+4) 10 =(00011)2
Le bit de signe '0' indique que la somme résultante est positive. Ainsi, sa magnitude est de 3 dans le système de nombres décimaux. Par conséquent, la soustraction de deux nombres décimaux +7 et +4 est +3.
Exemple 4
Laissez-nous effectuer le subtraction of deux nombres décimaux +4 et +7 en utilisant la méthode du complément à 2.
La soustraction de ces deux nombres est
(+4) 10 - (+7) 10 = (+4) 10 + (−7) 10 .
le 2’s complement La représentation de +4 et -7 avec 5 bits chacun est indiquée ci-dessous.
(+4) 10 = (00100) 2
(-7) 10 = (11001) 2
⇒ (+4) 10 + (-7) 10 = (00100) 2 + (11001) 2 = (11101) 2
Ici, le report n'est pas obtenu à partir du bit de signe. Le bit de signe '1' indique que la somme résultante estnegative. Ainsi, en prenant le complément de 2, nous obtiendrons la grandeur de la somme résultante égale à 3 dans le système de nombres décimaux. Par conséquent, la soustraction de deux nombres décimaux +4 et +7 est -3.
Dans le codage, lorsque des nombres ou des lettres sont représentés par un groupe spécifique de symboles, on dit que ce nombre ou cette lettre est en cours de codage. Le groupe de symboles est appelé commecode. Les données numériques sont représentées, stockées et transmises sous forme de groupe de bits. Ce groupe de bits est également appelébinary code.
Les codes binaires peuvent être classés en deux types.
- Codes pondérés
- Codes non pondérés
Si le code a des poids positionnels, on dit qu'il est weighted code. Sinon, c'est un code non pondéré. Les codes pondérés peuvent en outre être classés en codes pondérés positivement et en codes pondérés négativement.
Codes binaires pour les chiffres décimaux
Le tableau suivant présente les différents codes binaires pour les chiffres décimaux de 0 à 9.
| Chiffre décimal | 8421 Code | Code 2421 | Code 84-2-1 | Code excédentaire 3 |
|---|---|---|---|---|
| 0 | 0000 | 0000 | 0000 | 0011 |
| 1 | 0001 | 0001 | 0111 | 0100 |
| 2 | 0010 | 0010 | 0110 | 0101 |
| 3 | 0011 | 0011 | 0101 | 0110 |
| 4 | 0100 | 0100 | 0100 | 0111 |
| 5 | 0101 | 1011 | 1011 | 1000 |
| 6 | 0110 | 1100 | 1010 | 1001 |
| sept | 0111 | 1101 | 1001 | 1010 |
| 8 | 1000 | 1110 | 1000 | 1011 |
| 9 | 1001 | 1111 | 1111 | 1100 |
Nous avons 10 chiffres dans le système de nombre décimal. Pour représenter ces 10 chiffres en binaire, nous avons besoin d'un minimum de 4 bits. Mais, avec 4 bits, il y aura 16 combinaisons uniques de zéros et de uns. Depuis, nous n'avons que 10 chiffres décimaux, les 6 autres combinaisons de zéros et de uns ne sont pas nécessaires.
8 4 2 1 code
Les poids de ce code sont 8, 4, 2 et 1.
Ce code a tous les poids positifs. Donc, c'est unpositively weighted code.
Ce code est également appelé natural BCD (Décimal codé binaire) code.
Example
Trouvons l'équivalent BCD du nombre décimal 786. Ce nombre a 3 chiffres décimaux 7, 8 et 6. A partir du tableau, nous pouvons écrire les codes BCD (8421) de 7, 8 et 6 sont 0111, 1000 et 0110 respectivement .
∴ (786)10 = (011110000110)BCD
Il y a 12 bits dans la représentation BCD, puisque chaque code BCD de chiffre décimal a 4 bits.
2 4 2 1 code
Les poids de ce code sont 2, 4, 2 et 1.
Ce code a tous les poids positifs. Donc, c'est unpositively weighted code.
C'est un unnatural BCDcode. La somme des poids des codes BCD non naturels est égale à 9.
C'est un self-complementingcode. Les codes auto-complémentaires fournissent le complément 9 d'un nombre décimal, simplement en intervertissant les 1 et les 0 dans sa représentation équivalente 2421.
Example
Trouvons l'équivalent 2421 du nombre décimal 786. Ce nombre comporte 3 chiffres décimaux 7, 8 et 6. A partir du tableau, nous pouvons écrire les 2421 codes de 7, 8 et 6 sont 1101, 1110 et 1100 respectivement.
Par conséquent, l'équivalent 2421 du nombre décimal 786 est 110111101100.
8 4-2-1 code
Les poids de ce code sont 8, 4, -2 et -1.
Ce code a des poids négatifs ainsi que des poids positifs. Donc, c'est unnegatively weighted code.
C'est un unnatural BCD code.
C'est un self-complementing code.
Example
Trouvons l'équivalent 8 4-2-1 du nombre décimal 786. Ce nombre comporte 3 chiffres décimaux 7, 8 et 6. A partir du tableau, nous pouvons écrire les 8 4 -2 -1 codes de 7, 8 et 6 sont respectivement 1001, 1000 et 1010.
Par conséquent, l'équivalent 8 4 -2 -1 du nombre décimal 786 est 100110001010.
Code excédentaire 3
Ce code n'a pas de poids. Donc, c'est unun-weighted code.
Nous obtiendrons le code Excess 3 d'un nombre décimal en ajoutant trois (0011) à l'équivalent binaire de ce nombre décimal. Par conséquent, il est appelé code Excess 3.
C'est un self-complementing code.
Example
Trouvons l'équivalent Excess 3 du nombre décimal 786. Ce nombre a 3 chiffres décimaux 7, 8 et 6. À partir du tableau, nous pouvons écrire les codes Excess 3 de 7, 8 et 6 sont 1010, 1011 et 1001 respectivement.
Par conséquent, l'équivalent Excess 3 du nombre décimal 786 est 101010111001
Code gris
Le tableau suivant montre les codes Gray 4 bits correspondant à chaque code binaire 4 bits.
| Nombre décimal | Code binaire | Code gris |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| sept | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| dix | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
Ce code n'a pas de poids. Donc, c'est unun-weighted code.
Dans le tableau ci-dessus, les codes Gray successifs ne diffèrent que par une position de bit. Par conséquent, ce code est appelé commeunit distance code.
Binary code to Gray Code Conversion
Follow these steps for converting a binary code into its equivalent Gray code.
Consider the given binary code and place a zero to the left of MSB.
Compare the successive two bits starting from zero. If the 2 bits are same, then the output is zero. Otherwise, output is one.
Repeat the above step till the LSB of Gray code is obtained.
Example
From the table, we know that the Gray code corresponding to binary code 1000 is 1100. Now, let us verify it by using the above procedure.
Given, binary code is 1000.
Step 1 − By placing zero to the left of MSB, the binary code will be 01000.
Step 2 − By comparing successive two bits of new binary code, we will get the gray code as 1100.
We know that the bits 0 and 1 corresponding to two different range of analog voltages. So, during transmission of binary data from one system to the other, the noise may also be added. Due to this, there may be errors in the received data at other system.
That means a bit 0 may change to 1 or a bit 1 may change to 0. We can’t avoid the interference of noise. But, we can get back the original data first by detecting whether any error(s) present and then correcting those errors. For this purpose, we can use the following codes.
- Error detection codes
- Error correction codes
Error detection codes − are used to detect the error(s) present in the received data (bit stream). These codes contain some bit(s), which are included (appended) to the original bit stream. These codes detect the error, if it is occurred during transmission of the original data (bit stream).Example − Parity code, Hamming code.
Error correction codes − are used to correct the error(s) present in the received data (bit stream) so that, we will get the original data. Error correction codes also use the similar strategy of error detection codes.Example − Hamming code.
Therefore, to detect and correct the errors, additional bit(s) are appended to the data bits at the time of transmission.
Parity Code
It is easy to include (append) one parity bit either to the left of MSB or to the right of LSB of original bit stream. There are two types of parity codes, namely even parity code and odd parity code based on the type of parity being chosen.
Even Parity Code
The value of even parity bit should be zero, if even number of ones present in the binary code. Otherwise, it should be one. So that, even number of ones present in even parity code. Even parity code contains the data bits and even parity bit.
The following table shows the even parity codes corresponding to each 3-bit binary code. Here, the even parity bit is included to the right of LSB of binary code.
| Binary Code | Even Parity bit | Even Parity Code |
|---|---|---|
| 000 | 0 | 0000 |
| 001 | 1 | 0011 |
| 010 | 1 | 0101 |
| 011 | 0 | 0110 |
| 100 | 1 | 1001 |
| 101 | 0 | 1010 |
| 110 | 0 | 1100 |
| 111 | 1 | 1111 |
Here, the number of bits present in the even parity codes is 4. So, the possible even number of ones in these even parity codes are 0, 2 & 4.
If the other system receives one of these even parity codes, then there is no error in the received data. The bits other than even parity bit are same as that of binary code.
If the other system receives other than even parity codes, then there will be an error(s) in the received data. In this case, we can’t predict the original binary code because we don’t know the bit position(s) of error.
Therefore, even parity bit is useful only for detection of error in the received parity code. But, it is not sufficient to correct the error.
Odd Parity Code
The value of odd parity bit should be zero, if odd number of ones present in the binary code. Otherwise, it should be one. So that, odd number of ones present in odd parity code. Odd parity code contains the data bits and odd parity bit.
The following table shows the odd parity codes corresponding to each 3-bit binary code. Here, the odd parity bit is included to the right of LSB of binary code.
| Binary Code | Odd Parity bit | Odd Parity Code |
|---|---|---|
| 000 | 1 | 0001 |
| 001 | 0 | 0010 |
| 010 | 0 | 0100 |
| 011 | 1 | 0111 |
| 100 | 0 | 1000 |
| 101 | 1 | 1011 |
| 110 | 1 | 1101 |
| 111 | 0 | 1110 |
Here, the number of bits present in the odd parity codes is 4. So, the possible odd number of ones in these odd parity codes are 1 & 3.
If the other system receives one of these odd parity codes, then there is no error in the received data. The bits other than odd parity bit are same as that of binary code.
If the other system receives other than odd parity codes, then there is an error(s) in the received data. In this case, we can’t predict the original binary code because we don’t know the bit position(s) of error.
Therefore, odd parity bit is useful only for detection of error in the received parity code. But, it is not sufficient to correct the error.
Hamming Code
Hamming code is useful for both detection and correction of error present in the received data. This code uses multiple parity bits and we have to place these parity bits in the positions of powers of 2.
The minimum value of 'k' for which the following relation is correct (valid) is nothing but the required number of parity bits.
$$2^k\geq n+k+1$$
Where,
‘n’ is the number of bits in the binary code (information)
‘k’ is the number of parity bits
Therefore, the number of bits in the Hamming code is equal to n + k.
Let the Hamming code is $b_{n+k}b_{n+k-1}.....b_{3}b_{2}b_{1}$ & parity bits $p_{k}, p_{k-1}, ....p_{1}$. We can place the ‘k’ parity bits in powers of 2 positions only. In remaining bit positions, we can place the ‘n’ bits of binary code.
Based on requirement, we can use either even parity or odd parity while forming a Hamming code. But, the same parity technique should be used in order to find whether any error present in the received data.
Follow this procedure for finding parity bits.
Find the value of p1, based on the number of ones present in bit positions b3, b5, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 20.
Find the value of p2, based on the number of ones present in bit positions b3, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 21.
Find the value of p3, based on the number of ones present in bit positions b5, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 22.
Similarly, find other values of parity bits.
Follow this procedure for finding check bits.
Find the value of c1, based on the number of ones present in bit positions b1, b3, b5, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 20.
Find the value of c2, based on the number of ones present in bit positions b2, b3, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 21.
Find the value of c3, based on the number of ones present in bit positions b4, b5, b6, b7 and so on. All these bit positions (suffixes) in their equivalent binary have ‘1’ in the place value of 22.
Similarly, find other values of check bits.
The decimal equivalent of the check bits in the received data gives the value of bit position, where the error is present. Just complement the value present in that bit position. Therefore, we will get the original binary code after removing parity bits.
Example 1
Let us find the Hamming code for binary code, d4d3d2d1 = 1000. Consider even parity bits.
The number of bits in the given binary code is n=4.
We can find the required number of parity bits by using the following mathematical relation.
$$2^k\geq n+k+1$$
Substitute, n=4 in the above mathematical relation.
$$\Rightarrow 2^k\geq 4+k+1$$
$$\Rightarrow 2^k\geq 5+k$$
The minimum value of k that satisfied the above relation is 3. Hence, we require 3 parity bits p1, p2, and p3. Therefore, the number of bits in Hamming code will be 7, since there are 4 bits in binary code and 3 parity bits. We have to place the parity bits and bits of binary code in the Hamming code as shown below.
The 7-bit Hamming code is $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}=d_{4}d_{3}d_{2}p_{3}d_{1}p_{2}bp_{1}$
By substituting the bits of binary code, the Hamming code will be $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1} = 100p_{3}Op_{2}p_{1}$. Now, let us find the parity bits.
$$p_{1}=b_{7}\oplus b_{5}\oplus b_{3}=1 \oplus 0 \oplus 0=1$$
$$p_{2}=b_{7}\oplus b_{6}\oplus b_{3}=1 \oplus 0 \oplus 0=1$$
$$p_{3}=b_{7}\oplus b_{6}\oplus b_{5}=1 \oplus 0 \oplus 0=1$$
By substituting these parity bits, the Hamming code will be $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001011$.
Example 2
In the above example, we got the Hamming code as $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001011$. Now, let us find the error position when the code received is $b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}= 1001111$.
Now, let us find the check bits.
$$c_{1}=b_{7}\oplus b_{5}\oplus b_{3}\oplus b_{1}=1 \oplus 0 \oplus 1 \oplus1 =1$$
$$c_{2}=b_{7}\oplus b_{6}\oplus b_{3}\oplus b_{2}=1 \oplus 0 \oplus 1 \oplus1 =1$$
$$c_{3}=b_{7}\oplus b_{6}\oplus b_{5}\oplus b_{4}=1 \oplus 0 \oplus 0 \oplus1 =0$$
The decimal value of check bits gives the position of error in received Hamming code.
$$c_{3}c_{2}c_{1} = \left ( 011 \right )_{2}=\left ( 3 \right )_{10}$$
Therefore, the error present in third bit (b3) of Hamming code. Just complement the value present in that bit and remove parity bits in order to get the original binary code.
Boolean Algebra is an algebra, which deals with binary numbers & binary variables. Hence, it is also called as Binary Algebra or logical Algebra. A mathematician, named George Boole had developed this algebra in 1854. The variables used in this algebra are also called as Boolean variables.
The range of voltages corresponding to Logic ‘High’ is represented with ‘1’ and the range of voltages corresponding to logic ‘Low’ is represented with ‘0’.
Postulates and Basic Laws of Boolean Algebra
In this section, let us discuss about the Boolean postulates and basic laws that are used in Boolean algebra. These are useful in minimizing Boolean functions.
Boolean Postulates
Consider the binary numbers 0 and 1, Boolean variable (x) and its complement (x’). Either the Boolean variable or complement of it is known as literal. The four possible logical OR operations among these literals and binary numbers are shown below.
x + 0 = x
x + 1 = 1
x + x = x
x + x '= 1
De même, les quatre possibles logical AND les opérations parmi ces littéraux et nombres binaires sont indiquées ci-dessous.
x.1 = x
x.0 = 0
xx = x
x.x '= 0
Ce sont les postulats booléens simples. Nous pouvons vérifier ces postulats facilement, en remplaçant la variable booléenne par «0» ou «1».
Note- Le complément de complément de toute variable booléenne est égal à la variable elle-même. c'est-à-dire (x ')' = x.
Lois de base de l'algèbre booléenne
Voici les trois lois de base de l'algèbre booléenne.
- Loi commutative
- Droit associatif
- Loi distributive
Loi commutative
Si une opération logique de deux variables booléennes donne le même résultat quel que soit l'ordre de ces deux variables, alors cette opération logique est dite Commutative. Les opérations OR logiques et ET logiques de deux variables booléennes x et y sont indiquées ci-dessous
x + y = y + x
xy = yx
Le symbole «+» indique une opération OU logique. De même, le symbole «.» indique une opération ET logique et sa représentation est facultative. La loi commutative obéit aux opérations OU logiques et ET logiques.
Loi associative
Si une opération logique de deux variables booléennes quelconques est effectuée en premier et que la même opération est effectuée avec la variable restante donne le même résultat, alors cette opération logique est dite Associative. Les opérations OR logiques et ET logiques de trois variables booléennes x, y et z sont indiquées ci-dessous.
x + (y + z) = (x + y) + z
x. (yz) = (xy) .z
La loi associative obéit aux opérations OU logiques et ET logiques.
Loi distributive
Si une opération logique peut être distribuée à tous les termes présents dans la fonction booléenne, alors cette opération logique est dite Distributive. La distribution des opérations OR logiques et ET logiques de trois variables booléennes x, y et z est indiquée ci-dessous.
x. (y + z) = xy + xz
x + (yz) = (x + y). (x + z)
La loi distributive obéit aux opérations OU logiques et ET logiques.
Ce sont les lois de base de l'algèbre booléenne. Nous pouvons vérifier ces lois facilement, en remplaçant les variables booléennes par «0» ou «1».
Théorèmes de l'algèbre booléenne
Les deux théorèmes suivants sont utilisés en algèbre booléenne.
- Théorème de dualité
- Théorème de DeMorgan
Théorème de la dualité
Ce théorème stipule que le dualde la fonction booléenne est obtenue en interchangeant l'opérateur logique ET avec l'opérateur logique OU et les zéros avec des uns. Pour chaque fonction booléenne, il y aura une fonction Dual correspondante.
Faisons en deux groupes les équations booléennes (relations) dont nous avons parlé dans la section des postulats booléens et des lois de base. Le tableau suivant présente ces deux groupes.
| Groupe 1 | Groupe2 |
|---|---|
| x + 0 = x | x.1 = x |
| x + 1 = 1 | x.0 = 0 |
| x + x = x | xx = x |
| x + x '= 1 | x.x '= 0 |
| x + y = y + x | xy = yx |
| x + (y + z) = (x + y) + z | x. (yz) = (xy) .z |
| x. (y + z) = xy + xz | x + (yz) = (x + y). (x + z) |
Dans chaque ligne, il y a deux équations booléennes et elles sont doubles l'une par rapport à l'autre. Nous pouvons vérifier toutes ces équations booléennes de Group1 et Group2 en utilisant le théorème de dualité.
Théorème de DeMorgan
Ce théorème est utile pour trouver le complement of Boolean function. Il déclare que le complément du OU logique d'au moins deux variables booléennes est égal au ET logique de chaque variable complémentée.
Le théorème de DeMorgan avec 2 variables booléennes x et y peut être représenté comme
(x + y) '= x'.y'
Le dual de la fonction booléenne ci-dessus est
(xy) '= x' + y '
Par conséquent, le complément du ET logique de deux variables booléennes est égal au OU logique de chaque variable complémentée. De même, nous pouvons également appliquer le théorème de DeMorgan pour plus de 2 variables booléennes.
Simplification des fonctions booléennes
Jusqu'à présent, nous avons discuté des postulats, des lois de base et des théorèmes de l'algèbre booléenne. Maintenant, simplifions certaines fonctions booléennes.
Exemple 1
Laissez-nous simplify la fonction booléenne, f = p'qr + pq'r + pqr '+ pqr
Nous pouvons simplifier cette fonction de deux manières.
Method 1
Étant donné la fonction booléenne, f = p'qr + pq'r + pqr '+ pqr.
Step 1- En premier et deuxième termes, r est commun et en troisième et quatrième termes pq est commun. Alors, prenez les termes courants en utilisantDistributive law.
⇒ f = (p'q + pq ') r + pq (r' + r)
Step 2- Les termes présents dans la première parenthèse peuvent être simplifiés en fonctionnement Ex-OR. Les termes présents dans la deuxième parenthèse peuvent être simplifiés en «1» en utilisantBoolean postulate
⇒ f = (p ⊕q) r + pq (1)
Step 3- Le premier terme ne peut pas être simplifié davantage. Mais, le deuxième terme peut être simplifié en pq en utilisantBoolean postulate.
⇒ f = (p ⊕q) r + pq
Par conséquent, la fonction booléenne simplifiée est f = (p⊕q)r + pq
Method 2
Étant donné la fonction booléenne, f = p'qr + pq'r + pqr '+ pqr.
Step 1 - Utilisez le Boolean postulate, x + x = x. Cela signifie que l'opération OU logique avec n'importe quelle variable booléenne «n» fois sera égale à la même variable. Ainsi, nous pouvons écrire le dernier terme pqr deux fois de plus.
⇒ f = p'qr + pq'r + pqr '+ pqr + pqr + pqr
Step 2 - Utiliser Distributive lawpour 1 er et 4 ème termes, 2 ème et 5 ème termes, 3 ème et 6 ème termes.
⇒ f = qr (p '+ p) + pr (q' + q) + pq (r '+ r)
Step 3 - Utiliser Boolean postulate, x + x '= 1 pour simplifier les termes présents dans chaque parenthèse.
⇒ f = qr (1) + pr (1) + pq (1)
Step 4 - Utiliser Boolean postulate, x.1 = x pour simplifier les trois termes ci-dessus.
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
Par conséquent, la fonction booléenne simplifiée est f = pq + qr + pr.
Nous avons donc obtenu deux fonctions booléennes différentes après avoir simplifié la fonction booléenne donnée dans chaque méthode. Fonctionnellement, ces deux fonctions booléennes sont identiques. Ainsi, en fonction de l'exigence, nous pouvons choisir l'une de ces deux fonctions booléennes.
Exemple 2
Trouvons le complement de la fonction booléenne, f = p'q + pq '.
Le complément de la fonction booléenne est f '= (p'q + pq') '.
Step 1 - Utilisez le théorème de DeMorgan, (x + y) '= x'.y'.
⇒ f '= (p'q)'. (Pq ')'
Step 2 - Utiliser le théorème de DeMorgan, (xy) '= x' + y '
⇒ f '= {(p') '+ q'}. {P '+ (q') '}
Step3 - Utilisez le postulat booléen, (x ')' = x.
⇒ f '= {p + q'}. {P '+ q}
⇒ f '= pp' + pq + p'q '+ qq'
Step 4 - Utilisez le postulat booléen, xx '= 0.
⇒ f = 0 + pq + p'q '+ 0
⇒ f = pq + p'q '
Par conséquent, la complement de la fonction booléenne, p'q + pq 'est pq + p’q’.
Nous obtiendrons quatre termes de produit booléen en combinant deux variables x et y avec une opération ET logique. Ces termes de produit booléens sont appelésmin terms ou standard product terms. Les termes min sont x'y ', x'y, xy' et xy.
De même, nous obtiendrons quatre termes de somme booléenne en combinant deux variables x et y avec une opération OU logique. Ces termes de somme booléenne sont appelés commeMax terms ou standard sum terms. Les termes Max sont x + y, x + y ', x' + y et x '+ y'.
Le tableau suivant montre la représentation des termes min et des termes MAX pour 2 variables.
| X | y | Conditions minimales | Termes max |
|---|---|---|---|
| 0 | 0 | m 0 = x'y ' | M 0 = x + y |
| 0 | 1 | m 1 = x'y | M 1 = x + y ' |
| 1 | 0 | m 2 = xy ' | M 2 = x '+ y |
| 1 | 1 | m 3 = xy | M 3 = x '+ y' |
Si la variable binaire est '0', alors elle est représentée comme le complément de la variable en terme min et comme la variable elle-même dans le terme Max. De même, si la variable binaire est '1', alors elle est représentée comme complément de variable dans le terme Max et comme la variable elle-même dans le terme min.
À partir du tableau ci-dessus, nous pouvons facilement remarquer que les termes min et les termes Max sont complémentaires l'un de l'autre. S'il y a 'n' variables booléennes, alors il y aura 2 n termes min et 2 n termes Max.
Formulaires SoP et PoS canoniques
Une table de vérité se compose d'un ensemble d'entrées et de sorties. S'il y a 'n' variables d'entrée, alors il y aura 2 n combinaisons possibles avec des zéros et des uns. Ainsi, la valeur de chaque variable de sortie dépend de la combinaison des variables d'entrée. Ainsi, chaque variable de sortie aura «1» pour une combinaison de variables d'entrée et «0» pour une autre combinaison de variables d'entrée.
Par conséquent, nous pouvons exprimer chaque variable de sortie de deux manières.
- Formulaire SoP canonique
- Formulaire PoS canonique
Formulaire SoP canonique
La forme Canonical SoP signifie la forme Canonical Sum of Products. Sous cette forme, chaque terme de produit contient tous les littéraux. Donc, ces termes de produit ne sont rien d'autre que les termes minimum. Par conséquent, la forme canonique SoP est également appeléesum of min terms forme.
Tout d'abord, identifiez les termes min pour lesquels la variable de sortie est un, puis effectuez le OU logique de ces termes min afin d'obtenir l'expression booléenne (fonction) correspondant à cette variable de sortie. Cette fonction booléenne se présentera sous la forme d'une somme de termes min.
Suivez la même procédure pour les autres variables de sortie également, s'il y a plus d'une variable de sortie.
Exemple
Considérer ce qui suit truth table.
| Contributions | Production | ||
|---|---|---|---|
| p | q | r | f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Ici, la sortie (f) est «1» pour quatre combinaisons d'entrées. Les termes min correspondants sont p'qr, pq'r, pqr ', pqr. En faisant un OU logique de ces quatre termes min, nous obtiendrons la fonction booléenne de la sortie (f).
Par conséquent, la fonction booléenne de sortie est, f = p'qr + pq'r + pqr '+ pqr. C'est lecanonical SoP formde la sortie, f. Nous pouvons également représenter cette fonction en suivant deux notations.
$$f = m_{3}+m_{5}+m_{6}+m_{7}$$
$$f = \sum m\left ( 3,5,6,7 \right )$$
Dans une équation, nous avons représenté la fonction comme la somme des termes minimum respectifs. Dans une autre équation, nous avons utilisé le symbole pour la sommation de ces termes minimum.
Formulaire PoS canonique
La forme Canonical PoS signifie la forme Canonical Product of Sums. Sous cette forme, chaque terme de somme contient tous les littéraux. Donc, ces termes de somme ne sont rien d'autre que les termes Max. Par conséquent, la forme canonique de PoS est également appeléeproduct of Max terms forme.
Tout d'abord, identifiez les termes Max pour lesquels la variable de sortie est zéro, puis effectuez le ET logique de ces termes Max afin d'obtenir l'expression booléenne (fonction) correspondant à cette variable de sortie. Cette fonction booléenne se présentera sous la forme de produit de termes Max.
Suivez la même procédure pour les autres variables de sortie également, s'il y a plus d'une variable de sortie.
Example
Considérez la même table de vérité de l'exemple précédent. Ici, la sortie (f) est «0» pour quatre combinaisons d'entrées. Les termes Max correspondants sont p + q + r, p + q + r ', p + q' + r, p '+ q + r. En faisant un ET logique de ces quatre termes Max, nous obtiendrons la fonction booléenne de la sortie (f).
Par conséquent, la fonction booléenne de la sortie est, f = (p + q + r). (P + q + r '). (P + q' + r). (P '+ q + r). C'est lecanonical PoS formde la sortie, f. Nous pouvons également représenter cette fonction en suivant deux notations.
$$f=M_{0}.M_{1}.M_{2}.M_{4}$$
$$f=\prod M\left ( 0,1,2,4 \right )$$
Dans une équation, nous avons représenté la fonction comme le produit des termes Max respectifs. Dans une autre équation, nous avons utilisé le symbole pour la multiplication de ces termes Max.
La fonction booléenne, f = (p + q + r). (P + q + r '). (P + q' + r). (P '+ q + r) est le dual de la fonction booléenne, f = p'qr + pq'r + pqr '+ pqr.
Par conséquent, les formulaires SoP canoniques et PoS canoniques sont Dualles uns aux autres. Fonctionnellement, ces deux formes sont identiques. En fonction de l'exigence, nous pouvons utiliser l'un de ces deux formulaires.
Formulaires SoP et PoS standard
Nous avons discuté de deux formes canoniques de représentation de la ou des sorties booléennes. De même, il existe deux formes standard de représentation des sorties booléennes. Ce sont la version simplifiée des formes canoniques.
- Formulaire SoP standard
- Formulaire PoS standard
Nous discuterons des portes logiques dans les chapitres suivants. Le principaladvantagedes formes standard est que le nombre d'entrées appliquées aux portes logiques peut être minimisé. Parfois, il y aura une réduction du nombre total de portes logiques requises.
Formulaire SoP standard
Le formulaire SoP standard signifie Standard Sum of Productsforme. Sous cette forme, il n'est pas nécessaire que chaque terme de produit contienne tous les littéraux. Ainsi, les conditions du produit peuvent ou non être les conditions minimales. Par conséquent, le formulaire SoP standard est la forme simplifiée du formulaire SoP canonique.
Nous obtiendrons la forme Standard SoP de la variable de sortie en deux étapes.
- Obtenez la forme canonique SoP de la variable de sortie
- Simplifiez la fonction booléenne ci-dessus, qui se présente sous la forme canonique de SoP.
Suivez la même procédure pour les autres variables de sortie également, s'il y a plus d'une variable de sortie. Parfois, il n'est pas possible de simplifier le formulaire SoP canonique. Dans ce cas, les formulaires SoP canoniques et standard sont identiques.
Example
Convertissez la fonction booléenne suivante en un formulaire SoP standard.
f = p'qr + pq'r + pqr '+ pqr
La fonction booléenne donnée est sous la forme canonique de SoP. Maintenant, nous devons simplifier cette fonction booléenne afin d'obtenir un formulaire SoP standard.
Step 1 - Utilisez le Boolean postulate, x + x = x. Cela signifie que l'opération OU logique avec n'importe quelle variable booléenne «n» fois sera égale à la même variable. Ainsi, nous pouvons écrire le dernier terme pqr deux fois de plus.
⇒ f = p'qr + pq'r + pqr '+ pqr + pqr + pqr
Step 2 - Utiliser Distributive lawpour 1 er et 4 ème termes, 2 ème et 5 ème termes, 3 ème et 6 ème termes.
⇒ f = qr (p '+ p) + pr (q' + q) + pq (r '+ r)
Step 3 - Utiliser Boolean postulate, x + x '= 1 pour simplifier les termes présents dans chaque parenthèse.
⇒ f = qr (1) + pr (1) + pq (1)
Step 4 - Utiliser Boolean postulate, x.1 = x pour simplifier ci-dessus trois termes.
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
Il s'agit de la fonction booléenne simplifiée. Par conséquent, lastandard SoP form correspondant à une forme SoP canonique donnée est f = pq + qr + pr
Formulaire PoS standard
Formulaire PoS standard signifie Standard Product of Sumsforme. Sous cette forme, chaque terme de somme ne doit pas nécessairement contenir tous les littéraux. Ainsi, les termes de somme peuvent ou non être les termes Max. Par conséquent, le formulaire PoS standard est la forme simplifiée du formulaire PoS canonique.
Nous obtiendrons la forme PoS standard de la variable de sortie en deux étapes.
- Obtenez la forme PoS canonique de la variable de sortie
- Simplifiez la fonction booléenne ci-dessus, qui est sous forme canonique de PoS.
Suivez la même procédure pour les autres variables de sortie également, s'il y a plus d'une variable de sortie. Parfois, il n'est pas possible de simplifier le formulaire PoS canonique. Dans ce cas, les formulaires PoS canoniques et standard sont identiques.
Example
Convertissez la fonction booléenne suivante en un formulaire PoS standard.
f = (p + q + r). (p + q + r '). (p + q' + r). (p '+ q + r)
La fonction booléenne donnée est sous forme canonique de PoS. Maintenant, nous devons simplifier cette fonction booléenne afin d'obtenir un formulaire PoS standard.
Step 1 - Utilisez le Boolean postulate, xx = x. Cela signifie que l'opération ET logique avec n'importe quelle variable booléenne «n» fois sera égale à la même variable. Ainsi, nous pouvons écrire le premier terme p + q + r deux fois de plus.
⇒ f = (p + q + r). (P + q + r). (P + q + r). (P + q + r '). (P + q' + r). (P '+ q + r)
Step 2 - Utiliser Distributive law,x + (yz) = (x + y). (x + z) pour 1 ère et 4 ème parenthèse, 2 ème et 5 ème parenthèses, 3 ème et 6 ème parenthèses.
⇒ f = (p + q + rr '). (P + r + qq'). (Q + r + pp ')
Step 3 - Utiliser Boolean postulate, x.x '= 0 pour simplifier les termes présents dans chaque parenthèse.
⇒ f = (p + q + 0). (P + r + 0). (Q + r + 0)
Step 4 - Utiliser Boolean postulate, x + 0 = x pour simplifier les termes présents dans chaque parenthèse
⇒ f = (p + q). (P + r). (Q + r)
⇒ f = (p + q). (Q + r). (P + r)
Il s'agit de la fonction booléenne simplifiée. Par conséquent, lastandard PoS form correspondant à une forme de PoS canonique donnée est f = (p + q).(q + r).(p + r). C'est ledual de la fonction booléenne, f = pq + qr + pr.
Par conséquent, les formulaires SoP standard et PoS standard sont doubles les uns par rapport aux autres.
Dans les chapitres précédents, nous avons simplifié les fonctions booléennes en utilisant des postulats et théorèmes booléens. C'est un processus qui prend du temps et nous devons réécrire les expressions simplifiées après chaque étape.
Pour surmonter cette difficulté, Karnaughintroduit une méthode de simplification des fonctions booléennes de manière simple. Cette méthode est connue sous le nom de méthode de carte de Karnaugh ou méthode de K-map. C'est une méthode graphique, qui se compose de 2 n cellules pour «n» variables. Les cellules adjacentes ne diffèrent que par une position de bit unique.
K-Maps pour 2 à 5 variables
La méthode K-Map est la plus appropriée pour minimiser les fonctions booléennes de 2 variables à 5 variables. Maintenant, parlons des K-Maps pour 2 à 5 variables une par une.
2 K-Map variables
Le nombre de cellules dans 2 variables K-map est de quatre, puisque le nombre de variables est de deux. La figure suivante montre2 variable K-Map.
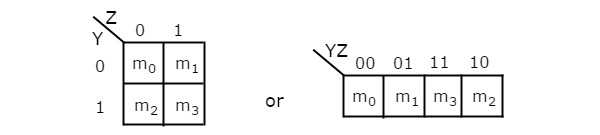
Il n'y a qu'une seule possibilité de regrouper 4 termes min adjacents.
Les combinaisons possibles de groupement de 2 termes min adjacents sont {(m 0 , m 1 ), (m 2 , m 3 ), (m 0 , m 2 ) et (m 1 , m 3 )}.
3 K-Map variables
Le nombre de cellules dans 3 variables K-map est de huit, puisque le nombre de variables est de trois. La figure suivante montre3 variable K-Map.
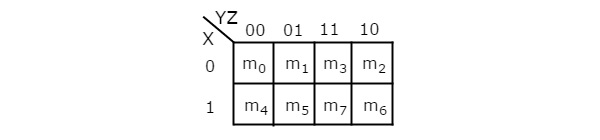
Il n'y a qu'une seule possibilité de regrouper 8 termes min adjacents.
Les combinaisons possibles de regroupement de 4 termes min adjacents sont {(m 0 , m 1 , m 3 , m 2 ), (m 4 , m 5 , m 7 , m 6 ), (m 0 , m 1 , m 4 , m 5 ), (m 1 , m 3 , m 5 , m 7 ), (m 3 , m 2 , m 7 , m 6 ) et (m 2 , m 0 , m 6 , m 4 )}.
Les combinaisons possibles de regroupement de 2 termes min adjacents sont {(m 0 , m 1 ), (m 1 , m 3 ), (m 3 , m 2 ), (m 2 , m 0 ), (m 4 , m 5 ) , (m 5 , m 7 ), (m 7 , m 6 ), (m 6 , m 4 ), (m 0 , m 4 ), (m 1 , m 5 ), (m 3 , m 7 ) et ( m 2 , m 6 )}.
Si x = 0, alors 3 variables K-map deviennent 2 variables K-map.
4 K-Map variables
Le nombre de cellules dans 4 variables K-map est de seize, puisque le nombre de variables est de quatre. La figure suivante montre4 variable K-Map.
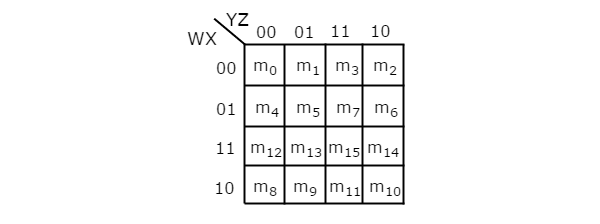
Il n'y a qu'une seule possibilité de regrouper 16 termes min adjacents.
Soit R 1 , R 2 , R 3 et R 4 les termes minimum de la première ligne, de la deuxième ligne, de la troisième ligne et de la quatrième ligne respectivement. De même, C 1 , C 2 , C 3 et C 4 représentent les termes minimum de la première colonne, de la deuxième colonne, de la troisième colonne et de la quatrième colonne respectivement. Les combinaisons possibles de regroupement de 8 termes min adjacents sont {(R 1 , R 2 ), (R 2 , R 3 ), (R 3 , R 4 ), (R 4 , R 1 ), (C 1 , C 2 ) , (C 2 , C 3 ), (C 3 , C 4 ), (C 4 , C 1 )}.
Si w = 0, alors 4 variables K-map deviennent 3 variables K-map.
5 K-Map variables
Le nombre de cellules dans 5 variables K-map est de trente-deux, puisque le nombre de variables est de 5. La figure suivante montre 5 variable K-Map.

Il n'y a qu'une seule possibilité de regrouper 32 termes min adjacents.
Il existe deux possibilités de regrouper 16 termes min adjacents. c'est-à-dire regroupement de termes min de m 0 à m 15 et m 16 à m 31 .
Si v = 0, alors 5 variables K-map deviennent 4 variables K-map.
Dans les K-maps ci-dessus, nous avons utilisé exclusivement la notation des termes min. De même, vous pouvez utiliser exclusivement la notation des termes Max.
Minimisation des fonctions booléennes à l'aide de K-Maps
Si nous considérons la combinaison d'entrées pour lesquelles la fonction booléenne est '1', alors nous obtiendrons la fonction booléenne, qui est dans standard sum of products forme après avoir simplifié la K-map.
De même, si nous considérons la combinaison d'entrées pour lesquelles la fonction booléenne est '0', alors nous obtiendrons la fonction booléenne, qui est dans standard product of sums forme après avoir simplifié la K-map.
Suivez ces rules for simplifying K-maps afin d'obtenir la somme standard des produits sous forme.
Sélectionnez la K-map respective en fonction du nombre de variables présentes dans la fonction booléenne.
Si la fonction booléenne est donnée sous forme de somme de termes minimum, placez les uns dans les cellules de terme minimum respectives dans la K-map. Si la fonction booléenne est donnée sous forme de somme de produits, placez celles-ci dans toutes les cellules possibles de K-map pour lesquelles les termes de produit donnés sont valides.
Vérifiez les possibilités de regrouper le nombre maximum de celles adjacentes. Ce devrait être des pouvoirs de deux. Commencez par la puissance la plus élevée de deux et jusqu'à la plus petite puissance de deux. La puissance la plus élevée est égale au nombre de variables considérées dans K-map et la puissance la plus faible est égale à zéro.
Chaque groupement donnera soit un terme littéral, soit un terme de produit. Il est connu commeprime implicant. On dit que l'impliquant principal estessential prime implicant, si au moins le «1» unique n'est couvert par aucun autre groupement, mais seulement ce groupement couvre.
Notez tous les implicants principaux et les implicants principaux essentiels. La fonction booléenne simplifiée contient tous les implicants principaux essentiels et uniquement les implicants principaux requis.
Note 1 - Si les sorties ne sont pas définies pour une combinaison d'entrées, ces valeurs de sortie seront représentées par don’t care symbol ‘x’. Cela signifie que nous pouvons les considérer comme «0» ou «1».
Note 2- Si les termes indifférents sont également présents, alors placez "x" indifférent dans les cellules respectives de la K-map. Considérez uniquement les «x» indifférents qui sont utiles pour regrouper le nombre maximal de ceux adjacents. Dans ces cas, traitez la valeur Don't Care comme «1».
Exemple
Laissez-nous simplify la fonction booléenne suivante, f(W, X, Y, Z)= WX’Y’ + WY + W’YZ’ en utilisant K-map.
La fonction booléenne donnée est sous forme de somme de produits. Il a 4 variables W, X, Y & Z. Donc, nous avons besoin4 variable K-map. le4 variable K-map avec ceux correspondant aux termes du produit donnés est montré dans la figure suivante.
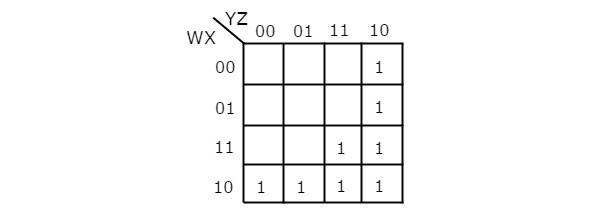
Ici, les 1 sont placés dans les cellules suivantes de la K-map.
Les cellules communes à l'intersection de la ligne 4 et des colonnes 1 et 2 correspondent au terme produit, WX’Y’.
Les cellules communes à l'intersection des rangées 3 et 4 et des colonnes 3 et 4 correspondent au terme produit, WY.
Les cellules communes à l'intersection des rangées 1 et 2 et de la colonne 4 correspondent au terme produit, W’YZ’.
Il n'y a pas de possibilité de regrouper 16 adjacents ou 8 adjacents. Il existe trois possibilités de regrouper 4 adjacentes. Après ces trois regroupements, il n'y en a plus un seul non groupé. Donc, nous n'avons pas besoin de vérifier le regroupement de 2 adjacents. le4 variable K-map avec ces trois groupings est illustré dans la figure suivante.

Ici, nous avons trois implicants principaux WX ', WY & YZ'. Tous ces principaux implicants sontessential pour les raisons suivantes.
Deux (m8 & m9)du groupe de quatrième rangée ne sont couverts par aucun autre regroupement. Seul le regroupement de la quatrième rangée couvre ces deux éléments.
Un seul (m15)du groupement de forme carrée n'est couvert par aucun autre groupement. Seul le groupement de forme carrée couvre celui-là.
Deux (m2 & m6)du groupement de la quatrième colonne ne sont couverts par aucun autre groupement. Seul le groupe de la quatrième colonne couvre ces deux éléments.
Par conséquent, la simplified Boolean function est
f = WX’ + WY + YZ’
Suivez ces rules for simplifying K-maps afin d'obtenir un produit standard sous forme de sommes.
Sélectionnez la K-map respective en fonction du nombre de variables présentes dans la fonction booléenne.
Si la fonction booléenne est donnée en tant que produit de la forme des termes Max, placez les zéros aux cellules des termes Max respectives dans la K-map. Si la fonction booléenne est donnée sous forme de produit de la forme des sommes, placez les zéros dans toutes les cellules possibles de K-map pour lesquelles les termes de somme donnés sont valides.
Vérifiez les possibilités de regrouper le nombre maximum de zéros adjacents. Ce devrait être des pouvoirs de deux. Commencez par la puissance la plus élevée de deux et jusqu'à la plus petite puissance de deux. La puissance la plus élevée est égale au nombre de variables considérées dans K-map et la puissance la plus faible est égale à zéro.
Chaque groupement donnera un terme littéral ou un terme de somme. Il est connu commeprime implicant. On dit que l'impliquant principal estessential prime implicant, si au moins le «0» unique n'est couvert par aucun autre groupement mais seulement ce groupement couvre.
Notez tous les implicants principaux et les implicants principaux essentiels. La fonction booléenne simplifiée contient tous les implicants principaux essentiels et uniquement les implicants principaux requis.
Note- Si les termes indifférents sont également présents, alors placez "x" indifférent dans les cellules respectives de la K-map. Considérez uniquement les «x» indifférents qui sont utiles pour regrouper le nombre maximum de zéros adjacents. Dans ces cas, traitez la valeur indifférente comme «0».
Exemple
Laissez-nous simplify la fonction booléenne suivante, $f\left ( X,Y,Z \right )=\prod M\left ( 0,1,2,4 \right )$ en utilisant K-map.
La fonction booléenne donnée est le produit de la forme Max terms. Il a 3 variables X, Y et Z. Donc, nous avons besoin de 3 variables K-map. Les termes Max donnés sont M 0 , M 1 , M 2 et M 4 . Le 3variable K-map avec des zéros correspondant aux termes Max donnés est montré dans la figure suivante.

Il n'y a pas de possibilité de regrouper 8 zéros adjacents ou 4 zéros adjacents. Il existe trois possibilités de regrouper 2 zéros adjacents. Après ces trois regroupements, il n'y a plus de zéro unique non groupé. le3 variable K-map avec ces trois groupings est illustré dans la figure suivante.

Ici, nous avons trois implicants premiers X + Y, Y + Z et Z + X. Tous ces implicants premiers sont essential car un zéro dans chaque groupement n'est couvert par aucun autre groupement, sauf avec leurs groupements individuels.
Par conséquent, la simplified Boolean function est
f = (X + Y).(Y + Z).(Z + X)
De cette façon, nous pouvons facilement simplifier les fonctions booléennes jusqu'à 5 variables en utilisant la méthode K-map. Pour plus de 5 variables, il est difficile de simplifier les fonctions à l'aide de K-Maps. Parce que, le nombre decells dans K-map obtient doubled en incluant une nouvelle variable.
En raison de cette vérification et le regroupement de ceux adjacents (termes minimum) ou de zéros adjacents (termes maximum) sera compliqué. Nous discuteronsTabular method dans le prochain chapitre pour surmonter les difficultés de la méthode K-map.
Dans le chapitre précédent, nous avons discuté de la méthode K-map, qui est une méthode pratique pour minimiser les fonctions booléennes jusqu'à 5 variables. Mais, il est difficile de simplifier les fonctions booléennes ayant plus de 5 variables en utilisant cette méthode.
La méthode tabulaire de Quine-McClukey est une méthode tabulaire basée sur le concept d'implicants premiers. Nous savons queprime implicant est un terme produit (ou somme), qui ne peut pas être réduit davantage en le combinant avec tout autre terme produit (ou somme) de la fonction booléenne donnée.
Cette méthode tabulaire est utile pour obtenir les principaux implicants en utilisant à plusieurs reprises l'identité booléenne suivante.
xy + xy '= x (y + y') = x.1 = x
Procédure de la méthode tabulaire Quine-McCluskey
Suivez ces étapes pour simplifier les fonctions booléennes à l'aide de la méthode tabulaire Quine-McClukey.
Step 1 - Organiser les termes minimum donnés dans un ascending orderet faites les groupes en fonction du nombre de ceux présents dans leurs représentations binaires. Alors, il y auraat most ‘n+1’ groups s'il y a 'n' variables booléennes dans une fonction booléenne ou 'n' bits dans l'équivalent binaire de termes min.
Step 2 - Comparez les termes minimum présents dans successive groups. S'il y a un changement dans la position d'un bit seulement, prenez la paire de ces deux termes min. Placez ce symbole '_' dans la position de bit différée et conservez les bits restants tels quels.
Step 3 - Répétez l'étape 2 avec les termes nouvellement formés jusqu'à ce que nous ayons tous prime implicants.
Step 4 - Formuler le prime implicant table. Il se compose d'un ensemble de lignes et de colonnes. Les implicants Prime peuvent être placés en rangées et les termes minimum peuvent être placés en colonnes. Placez '1' dans les cellules correspondant aux termes min qui sont couverts dans chaque implicant premier.
Step 5- Trouvez les principaux implicants essentiels en observant chaque colonne. Si le terme minimum n'est couvert que par un seul implicant premier, alors il estessential prime implicant. Ces implicants principaux essentiels feront partie de la fonction booléenne simplifiée.
Step 6- Réduire la table des implicants premiers en supprimant la ligne de chaque implicant premier essentiel et les colonnes correspondant aux termes min qui sont couverts dans cet implicant premier essentiel. Répétez l'étape 5 pour la table d'implication primaire réduite. Arrêtez ce processus lorsque tous les termes minimum d'une fonction booléenne donnée sont terminés.
Exemple
Laissez-nous simplify la fonction booléenne suivante, $f\left ( W,X,Y,Z \right )=\sum m\left ( 2,6,8,9,10,11,14,15 \right )$ en utilisant la méthode tabulaire Quine-McClukey.
La fonction booléenne donnée est dans sum of min termsforme. Il a 4 variables W, X, Y & Z. Les termes min donnés sont 2, 6, 8, 9, 10, 11, 14 et 15. L'ordre croissant de ces termes min en fonction du nombre de termes présents dans leur l'équivalent binaire est 2, 8, 6, 9, 10, 11, 14 et 15. Le tableau suivant montre cesmin terms and their equivalent binary représentations.
| Nom de groupe | Conditions minimales | W | X | Oui | Z |
|---|---|---|---|---|---|
| GA1 | 2 | 0 | 0 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | |
| GA2 | 6 | 0 | 1 | 1 | 0 |
| 9 | 1 | 0 | 0 | 1 | |
| dix | 1 | 0 | 1 | 0 | |
| 11 | 1 | 0 | 1 | 1 | |
| 14 | 1 | 1 | 1 | 0 | |
| GA4 | 15 | 1 | 1 | 1 | 1 |
Les termes minimum donnés sont classés en 4 groupes en fonction du nombre de termes présents dans leurs équivalents binaires. Le tableau suivant montre lesmerging of min terms des groupes adjacents.
| Nom de groupe | Conditions minimales | W | X | Oui | Z |
|---|---|---|---|---|---|
| GB1 | 2,6 | 0 | - | 1 | 0 |
| 2,10 | - | 0 | 1 | 0 | |
| 8,9 | 1 | 0 | 0 | - | |
| 8,10 | 1 | 0 | - | 0 | |
| GB2 | 6,14 | - | 1 | 1 | 0 |
| 9,11 | 1 | 0 | - | 1 | |
| 10,11 | 1 | 0 | 1 | - | |
| 10,14 | 1 | - | 1 | 0 | |
| 11,15 | 1 | - | 1 | 1 | |
| 14,15 | 1 | 1 | 1 | - |
Les termes min, qui ne diffèrent que par une position d'un bit des groupes adjacents, sont fusionnés. Ce bit différent est représenté par ce symbole, «-». Dans ce cas, il y a trois groupes et chaque groupe contient des combinaisons de deux termes minimum. Le tableau suivant montre lesmerging of min term pairs des groupes adjacents.
| Nom de groupe | Conditions minimales | W | X | Oui | Z |
|---|---|---|---|---|---|
| GB1 | 2,6,10,14 | - | - | 1 | 0 |
| 2,10,6,14 | - | - | 1 | 0 | |
| 8,9,10,11 | 1 | 0 | - | - | |
| 8,10,9,11 | 1 | 0 | - | - | |
| GB2 | 10,11,14,15 | 1 | - | 1 | - |
| 10,14,11,15 | 1 | - | 1 | - |
Les groupes successifs de paires de termes minimum, qui ne diffèrent que par une position d'un bit, sont fusionnés. Ce bit différent est représenté par ce symbole, «-». Dans ce cas, il y a deux groupes et chaque groupe contient des combinaisons de quatre termes min. Ici, ces combinaisons de termes de 4 min sont disponibles sur deux lignes. Ainsi, nous pouvons supprimer les lignes répétées. Le tableau réduit après suppression des lignes redondantes est illustré ci-dessous.
| Nom de groupe | Conditions minimales | W | X | Oui | Z |
|---|---|---|---|---|---|
| GC1 | 2,6,10,14 | - | - | 1 | 0 |
| 8,9,10,11 | 1 | 0 | - | - | |
| GC2 | 10,11,14,15 | 1 | - | 1 | - |
Une fusion supplémentaire des combinaisons de termes min provenant de groupes adjacents n'est pas possible, car ils sont différés sur plus d'un bit. Il y a trois lignes dans le tableau ci-dessus. Ainsi, chaque ligne donnera un implicant principal. Par conséquent, laprime implicants sont YZ ', WX' et WY.
le prime implicant table est illustré ci-dessous.
| Conditions minimales / Implicants Prime | 2 | 6 | 8 | 9 | dix | 11 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|
| YZ’ | 1 | 1 | 1 | 1 | ||||
| WX’ | 1 | 1 | 1 | 1 | ||||
| WY | 1 | 1 | 1 | 1 |
Les principaux implicants sont placés par ligne et les termes minimum sont placés par colonne. Les 1 sont placés dans les cellules communes des premières lignes d'implication et des colonnes de terme minimum correspondantes.
Les termes minimum 2 et 6 ne sont couverts que par un seul implicant premier YZ’. Donc, c'est unessential prime implicant. Cela fera partie de la fonction booléenne simplifiée. Maintenant, supprimez cette ligne implicante principale et les colonnes de terme minimum correspondantes. Le tableau d'implants primaires réduits est présenté ci-dessous.
| Conditions minimales / Implicants Prime | 8 | 9 | 11 | 15 |
|---|---|---|---|---|
| WX’ | 1 | 1 | 1 | |
| WY | 1 | 1 |
Les termes minimum 8 et 9 ne sont couverts que par un seul implicant premier WX’. Donc, c'est unessential prime implicant. Cela fera partie de la fonction booléenne simplifiée. Maintenant, supprimez cette ligne implicante principale et les colonnes de terme minimum correspondantes. Le tableau d'implants primaires réduits est présenté ci-dessous.
| Conditions minimales / Implicants Prime | 15 |
|---|---|
| WY | 1 |
Le terme minimum 15 n'est couvert que par un seul implicant premier WY. Donc, c'est unessential prime implicant. Cela fera partie de la fonction booléenne simplifiée.
Dans cet exemple de problème, nous avons trois implicants principaux et tous les trois sont essentiels. Par conséquent, lasimplified Boolean function est
f(W,X,Y,Z) = YZ’ + WX’ + WY.
Les circuits électroniques numériques fonctionnent avec des tensions de two logic levelsà savoir Logic Low et Logic High. La plage de tensions correspondant à Logic Low est représentée par «0». De même, la plage de tensions correspondant à Logic High est représentée par «1».
Le circuit électronique numérique de base qui a une ou plusieurs entrées et une seule sortie est appelé Logic gate. Par conséquent, les portes logiques sont les éléments constitutifs de tout système numérique. Nous pouvons classer ces portes logiques dans les trois catégories suivantes.
- Portes de base
- Portails universels
- Portes spéciales
Maintenant, laissez-nous discuter des portes logiques sous chaque catégorie une par une.
Portes de base
Dans les chapitres précédents, nous avons appris que les fonctions booléennes peuvent être représentées soit sous forme de somme de produits, soit sous forme de produit de somme en fonction de l'exigence. Ainsi, nous pouvons implémenter ces fonctions booléennes en utilisant des portes de base. Les portes de base sont des portes ET, OU ET NON.
ET porte
Une porte ET est un circuit numérique qui a deux entrées ou plus et produit une sortie, qui est le logical ANDde toutes ces entrées. Il est facultatif de représenter leLogical AND avec le symbole «.».
Le tableau suivant montre les truth table de la porte ET à 2 entrées.
| UNE | B | Y = AB |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Ici, A, B sont les entrées et Y est la sortie de deux portes ET d'entrée. Si les deux entrées sont «1», alors seule la sortie, Y est «1». Pour les combinaisons d'entrées restantes, la sortie, Y est «0».
La figure suivante montre le symbol d'une porte ET, qui a deux entrées A, B et une sortie, Y.

Cette porte ET produit une sortie (Y), qui est le logical ANDde deux entrées A, B. De même, s'il y a 'n' entrées, alors la porte ET produit une sortie, qui est le ET logique de toutes ces entrées. Cela signifie que la sortie de la porte ET sera «1», lorsque toutes les entrées seront «1».
OU porte
An OR gate is a digital circuit that has two or more inputs and produces an output, which is the logical OR of all those inputs. This logical OR is represented with the symbol ‘+’.
The following table shows the truth table of 2-input OR gate.
| A | B | Y = A + B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Here A, B are the inputs and Y is the output of two input OR gate. If both inputs are ‘0’, then only the output, Y is ‘0’. For remaining combinations of inputs, the output, Y is ‘1’.
The following figure shows the symbol of an OR gate, which is having two inputs A, B and one output, Y.

This OR gate produces an output (Y), which is the logical OR of two inputs A, B. Similarly, if there are ‘n’ inputs, then the OR gate produces an output, which is the logical OR of all those inputs. That means, the output of an OR gate will be ‘1’, when at least one of those inputs is ‘1’.
NOT gate
A NOT gate is a digital circuit that has single input and single output. The output of NOT gate is the logical inversion of input. Hence, the NOT gate is also called as inverter.
The following table shows the truth table of NOT gate.
| A | Y = A’ |
|---|---|
| 0 | 1 |
| 1 | 0 |
Here A and Y are the input and output of NOT gate respectively. If the input, A is ‘0’, then the output, Y is ‘1’. Similarly, if the input, A is ‘1’, then the output, Y is ‘0’.
The following figure shows the symbol of NOT gate, which is having one input, A and one output, Y.

This NOT gate produces an output (Y), which is the complement of input, A.
Universal gates
NAND & NOR gates are called as universal gates. Because we can implement any Boolean function, which is in sum of products form by using NAND gates alone. Similarly, we can implement any Boolean function, which is in product of sums form by using NOR gates alone.
NAND gate
NAND gate is a digital circuit that has two or more inputs and produces an output, which is the inversion of logical AND of all those inputs.
The following table shows the truth table of 2-input NAND gate.
| A | B | Y = (A.B)’ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output of two input NAND gate. When both inputs are ‘1’, the output, Y is ‘0’. If at least one of the input is zero, then the output, Y is ‘1’. This is just opposite to that of two input AND gate operation.
The following image shows the symbol of NAND gate, which is having two inputs A, B and one output, Y.
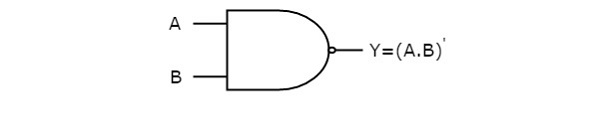
NAND gate operation is same as that of AND gate followed by an inverter. That’s why the NAND gate symbol is represented like that.
NOR gate
NOR gate is a digital circuit that has two or more inputs and produces an output, which is the inversion of logical OR of all those inputs.
The following table shows the truth table of 2-input NOR gate
| A | B | Y = (A+B)’ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output. If both inputs are ‘0’, then the output, Y is ‘1’. If at least one of the input is ‘1’, then the output, Y is ‘0’. This is just opposite to that of two input OR gate operation.
The following figure shows the symbol of NOR gate, which is having two inputs A, B and one output, Y.

NOR gate operation is same as that of OR gate followed by an inverter. That’s why the NOR gate symbol is represented like that.
Special Gates
Ex-OR & Ex-NOR gates are called as special gates. Because, these two gates are special cases of OR & NOR gates.
Ex-OR gate
The full form of Ex-OR gate is Exclusive-OR gate. Its function is same as that of OR gate except for some cases, when the inputs having even number of ones.
The following table shows the truth table of 2-input Ex-OR gate.
| A | B | Y = A⊕B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output of two input Ex-OR gate. The truth table of Ex-OR gate is same as that of OR gate for first three rows. The only modification is in the fourth row. That means, the output (Y) is zero instead of one, when both the inputs are one, since the inputs having even number of ones.
Therefore, the output of Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero, when both inputs are same.
Below figure shows the symbol of Ex-OR gate, which is having two inputs A, B and one output, Y.

Ex-OR gate operation is similar to that of OR gate, except for few combination(s) of inputs. That’s why the Ex-OR gate symbol is represented like that. The output of Ex-OR gate is ‘1’, when odd number of ones present at the inputs. Hence, the output of Ex-OR gate is also called as an odd function.
Ex-NOR gate
The full form of Ex-NOR gate is Exclusive-NOR gate. Its function is same as that of NOR gate except for some cases, when the inputs having even number of ones.
The following table shows the truth table of 2-input Ex-NOR gate.
| A | B | Y = A⊙B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Here A, B are the inputs and Y is the output. The truth table of Ex-NOR gate is same as that of NOR gate for first three rows. The only modification is in the fourth row. That means, the output is one instead of zero, when both the inputs are one.
Therefore, the output of Ex-NOR gate is ‘1’, when both inputs are same. And it is zero, when both the inputs are different.
The following figure shows the symbol of Ex-NOR gate, which is having two inputs A, B and one output, Y.

Ex-NOR gate operation is similar to that of NOR gate, except for few combination(s) of inputs. That’s why the Ex-NOR gate symbol is represented like that. The output of Ex-NOR gate is ‘1’, when even number of ones present at the inputs. Hence, the output of Ex-NOR gate is also called as an even function.
From the above truth tables of Ex-OR & Ex-NOR logic gates, we can easily notice that the Ex-NOR operation is just the logical inversion of Ex-OR operation.
The maximum number of levels that are present between inputs and output is two in two level logic. That means, irrespective of total number of logic gates, the maximum number of Logic gates that are present (cascaded) between any input and output is two in two level logic. Here, the outputs of first level Logic gates are connected as inputs of second level Logic gate(s).
Consider the four Logic gates AND, OR, NAND & NOR. Since, there are 4 Logic gates, we will get 16 possible ways of realizing two level logic. Those are AND-AND, AND-OR, ANDNAND, AND-NOR, OR-AND, OR-OR, OR-NAND, OR-NOR, NAND-AND, NAND-OR, NANDNAND, NAND-NOR, NOR-AND, NOR-OR, NOR-NAND, NOR-NOR.
These two level logic realizations can be classified into the following two categories.
- Degenerative form
- Non-degenerative form
Degenerative Form
If the output of two level logic realization can be obtained by using single Logic gate, then it is called as degenerative form. Obviously, the number of inputs of single Logic gate increases. Due to this, the fan-in of Logic gate increases. This is an advantage of degenerative form.
Only 6 combinations of two level logic realizations out of 16 combinations come under degenerative form. Those are AND-AND, AND-NAND, OR-OR, OR-NOR, NAND-NOR, NORNAND.
In this section, let us discuss some realizations. Assume, A, B, C & D are the inputs and Y is the output in each logic realization.
AND-AND Logic
In this logic realization, AND gates are present in both levels. Below figure shows an example for AND-AND logic realization.

We will get the outputs of first level logic gates as $Y_{1}=AB$ and $Y_{2}=CD$
These outputs, $Y_{1}$ and $Y_{2}$ are applied as inputs of AND gate that is present in second level. So, the output of this AND gate is
$$Y=Y_{1}Y_{2}$$
Substitute $Y_{1}$ and $Y_{2}$ values in the above equation.
$$Y=\left ( AB \right )\left ( CD \right )$$
$\Rightarrow Y=ABCD$
Therefore, the output of this AND-AND logic realization is ABCD. This Boolean function can be implemented by using a 4 input AND gate. Hence, it is degenerative form.
AND-NAND Logic
In this logic realization, AND gates are present in first level and NAND gate(s) are present in second level. The following figure shows an example for AND-NAND logic realization.
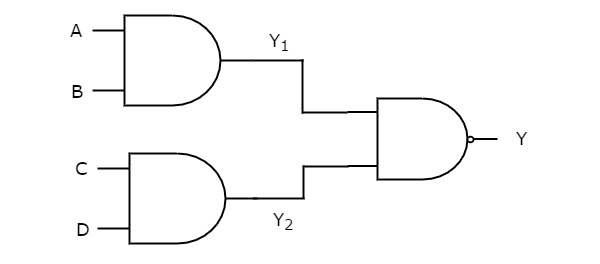
Auparavant, nous obtenions les sorties des portes logiques de premier niveau comme $Y_{1} = AB$ et $Y_{2} = CD$
Ces sorties,$Y_{1}$ et $Y_{2}$sont appliqués en tant qu'entrées de la porte NAND présente au deuxième niveau. Ainsi, la sortie de cette porte NAND est
$$Y={\left ( Y_{1}Y_{2} \right )}'$$
Remplacer $Y_{1}$ et $Y_{2}$ valeurs dans l'équation ci-dessus.
$$Y={\left ( \left ( AB \right ) \left ( CD \right )\right )}'$$
$\Rightarrow Y={\left ( ABCD \right )}'$
Par conséquent, la sortie de cette réalisation logique AND-NAND est ${\left ( ABCD \right )}'$. Cette fonction booléenne peut être implémentée en utilisant une porte NAND à 4 entrées. Par conséquent, c'estdegenerative form.
Logique OR-OR
Dans cette réalisation logique, les portes OU sont présentes dans les deux niveaux. La figure suivante montre un exemple deOR-OR logic la concrétisation.
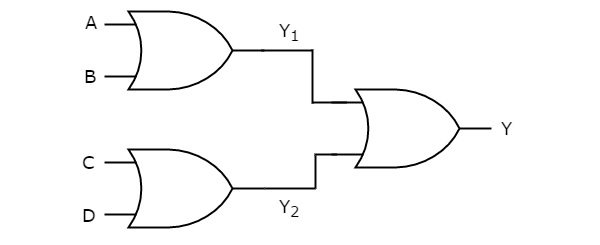
Nous obtiendrons les sorties des portes logiques de premier niveau comme $Y_{1}=A+B$ et $Y_{2}=C+D$.
Ces sorties, $Y_{1}$ et $Y_{2}$sont appliqués en tant qu'entrées de la porte OU qui est présente au deuxième niveau. Ainsi, la sortie de cette porte OU est
$$Y=Y_{1}+Y_{2}$$
Remplacer $Y_{1}$ et $Y_{2}$ valeurs dans l'équation ci-dessus.
$$Y=\left ( A+B \right )+\left ( C+D \right )$$
$\Rightarrow Y=A+B+C+D$
Par conséquent, la sortie de cette réalisation logique OU-OU est A+B+C+D. Cette fonction booléenne peut être implémentée en utilisant une porte OU à 4 entrées. Par conséquent, c'estdegenerative form.
De même, vous pouvez vérifier si les réalisations restantes appartiennent ou non à cette catégorie.
Forme non dégénérative
Si la sortie de la réalisation logique à deux niveaux ne peut pas être obtenue en utilisant une porte logique unique, alors elle est appelée comme non-degenerative form.
Le reste 10 combinationsdes réalisations logiques à deux niveaux se présentent sous forme non dégénérative. Ce sont AND-OR, AND-NOR, OR-AND, OR-NAND, NAND-AND, NANDOR, NAND-NAND, NOR-AND, NOR-OR, NOR-NOR.
Maintenant, parlons de quelques réalisations. Supposons que A, B, C et D sont les entrées et Y est la sortie dans chaque réalisation logique.
Logique AND-OR
Dans cette réalisation logique, les portes ET sont présentes au premier niveau et les portes OU sont présentes au deuxième niveau. La figure ci-dessous montre un exemple pourAND-OR logic la concrétisation.

Auparavant, nous obtenions les sorties des portes logiques de premier niveau comme $Y_{1} = AB$ et $Y_{2} = CD$.
Ces sorties Y1 et Y2 sont appliquées en tant qu'entrées de la porte OU qui est présente au deuxième niveau. Ainsi, la sortie de cette porte OU est
$$Y=Y_{1}+Y_{2}$$
Remplacer $Y_{1}$ et $Y_{2}$ valeurs dans l'équation ci-dessus
$$Y=AB+CD$$
Par conséquent, la sortie de cette réalisation logique ET-OU est AB+CD. Cette fonction booléenne est enSum of Productsforme. Puisque nous ne pouvons pas l'implémenter en utilisant une seule porte logique, cette réalisation logique ET-OU est unnon-degenerative form.
Logique AND-NOR
Dans cette réalisation logique, les portes ET sont présentes au premier niveau et la ou les portes NOR sont présentes au deuxième niveau. La figure suivante montre un exemple deAND-NOR logic la concrétisation.

Nous connaissons les sorties des portes logiques de premier niveau comme $Y_{1} = AB$ et $Y_{2} = CD$
Ces sorties Y1 et Y2 sont appliquées en tant qu'entrées de la porte NOR qui est présente au deuxième niveau. Ainsi, la sortie de cette porte NOR est
$$Y={\left ( Y_{1}+Y_{2} \right )}'$$
Remplacer $Y_{1}$ et $Y_{2}$ valeurs dans l'équation ci-dessus.
$$Y={\left ( AB+CD \right )}'$$
Par conséquent, la sortie de cette réalisation logique AND-NOR est ${\left ( AB+CD \right )}'$. Cette fonction booléenne est enAND-OR-Invertforme. Puisque nous ne pouvons pas l'implémenter en utilisant une seule porte logique, cette réalisation logique AND-NOR est unnon-degenerative form
Logique OU-ET
Dans cette réalisation logique, les portes OU sont présentes dans le premier niveau et la ou les portes ET sont présentes dans le deuxième niveau. La figure suivante montre un exemple deOR-AND logic la concrétisation.

Auparavant, nous obtenions les sorties des portes logiques de premier niveau comme $Y_{1}=A+B$ et $Y_{2}=C+D$.
Ces sorties, $Y_{1}$ et $Y_{2}$sont appliquées en tant qu'entrées de la porte ET présente au deuxième niveau. Ainsi, la sortie de cette porte ET est
$$Y=Y_{1}Y_{2}$$
Remplacer $Y_{1}$ et $Y_{2}$ valeurs dans l'équation ci-dessus.
$$Y = \left ( A+B \right )\left ( C+D \right )$$
Par conséquent, la sortie de cette réalisation logique OU-ET est (A + B) (C + D). Cette fonction booléenne est enProduct of Sumsforme. Puisque nous ne pouvons pas l'implémenter en utilisant une seule porte logique, cette réalisation logique OU-ET est unnon-degenerative form.
De même, vous pouvez vérifier si les réalisations restantes appartiennent ou non à cette catégorie.
Combinational circuitsse composent de portes logiques. Ces circuits fonctionnent avec des valeurs binaires. La (les) sortie (s) du circuit combinatoire dépend de la combinaison des entrées présentes. La figure suivante montre leblock diagram de circuit combinatoire.

Ce circuit combinatoire a «n» variables d'entrée et «m» sorties. Chaque combinaison de variables d'entrée affectera la ou les sorties.
Procédure de conception des circuits combinés
Trouvez le nombre requis de variables d'entrée et de sorties à partir de spécifications données.
Formulez le Truth table. S'il y a 'n' variables d'entrée, alors il y aura 2n combinaisons possibles. Pour chaque combinaison d'entrée, recherchez les valeurs de sortie.
Trouvez le Boolean expressionspour chaque sortie. Si nécessaire, simplifiez ces expressions.
Implémentez les expressions booléennes ci-dessus correspondant à chaque sortie en utilisant Logic gates.
Convertisseurs de code
Nous avons discuté de divers codes dans le chapitre intitulé codes. Les convertisseurs, qui convertissent un code en un autre code sont appelés commecode converters. Ces convertisseurs de code se composent essentiellement de portes logiques.
Exemple
Convertisseur de code binaire en code Gray
Implémentons un convertisseur, qui convertit un code binaire 4 bits WXYZ en son équivalent Gray code ABCD.
Le tableau suivant montre les Truth table d'un convertisseur de code binaire 4 bits en code Gray.
| Code binaire WXYZ | WXYZ Code gris ABCD |
|---|---|
| 0000 | 0000 |
| 0001 | 0001 |
| 0010 | 0011 |
| 0011 | 0010 |
| 0100 | 0110 |
| 0101 | 0111 |
| 0110 | 0101 |
| 0111 | 0100 |
| 1000 | 1100 |
| 1001 | 1101 |
| 1010 | 1111 |
| 1011 | 1110 |
| 1100 | 1010 |
| 1101 | 1011 |
| 1110 | 1001 |
| 1111 | 1000 |
À partir de la table de vérité, nous pouvons écrire le Boolean functions pour chaque bit de sortie du code Gray comme ci-dessous.
$$A=\sum m\left (8,9,10,11,12,13,14,15 \right )$$
$$B=\sum m\left (4,5,6,7,8,9,10,11 \right )$$
$$C=\sum m\left (2,3,4,5,10,11,12,13 \right )$$
$$D=\sum m\left (1,2,5,6,9,10,13,14 \right )$$
Simplifions les fonctions ci-dessus en utilisant 4 K-Maps variables.
La figure suivante montre le 4 variable K-Map pour simplifier Boolean function, A.

En regroupant 8 adjacentes, on obtient $A=W$.
La figure suivante montre le 4 variable K-Map pour simplifier Boolean function, B.

Il y a deux groupes de 4 adjacents. Après le regroupement, nous obtiendrons B comme
$$B={W}'X+W{X}'=W\oplus X $$
De même, nous obtiendrons les fonctions booléennes suivantes pour C & D après avoir simplifié.
$$C={X}'Y+X{Y}'=X \oplus Y$$
$$D={Y}'Z+Y{Z}'=Y \oplus Z$$
La figure suivante montre le circuit diagram de code binaire 4 bits au convertisseur de code Gray.

Étant donné que les sorties ne dépendent que des entrées présentes, ce convertisseur de code binaire à code Gray à 4 bits est un circuit combinatoire. De même, vous pouvez implémenter d'autres convertisseurs de code.
Générateur de bits de parité
Il existe deux types de générateurs de bits de parité en fonction du type de bit de parité généré. Even parity generatorgénère un bit de parité pair. De même,odd parity generator génère un bit de parité impair.
Générateur de parité paire
Maintenant, implémentons un générateur de parité paire pour une entrée binaire 3 bits, WXY. Il génère un bit de parité pair, P. Si un nombre impair de uns est présent dans l'entrée, alors le bit de parité pair, P doit être égal à «1» afin que le mot résultant contienne un nombre pair de uns. Pour d'autres combinaisons d'entrée, même bit de parité, P doit être «0». Le tableau suivant montre lesTruth table du générateur de parité paire.
| Entrée binaire WXY | Bit de parité paire P |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 1 |
| 011 | 0 |
| 100 | 1 |
| 101 | 0 |
| 110 | 0 |
| 111 | 1 |
À partir du tableau de vérité ci-dessus, nous pouvons écrire le Boolean function pour un bit de parité pair comme
$$P={W}'{X}'Y+{W}'X{Y}'+W{X}'{Y}'+WXY$$
$\Rightarrow P={W}'\left ( {X}'Y+X{Y}' \right )+W\left ({X}'{Y}'+XY \right )$
$\Rightarrow P={W}'\left ( X \oplus Y \right )+W{\left (X \oplus Y \right )}'=W \oplus X \oplus Y$
La figure suivante montre le circuit diagram du générateur de parité paire.

Ce circuit se compose de deux Exclusive-OR gatesayant deux entrées chacun. Première porte ExclusiveOR ayant deux entrées W & X et produit une sortie W ⊕ X. Cette sortie est donnée comme une entrée de la seconde porte Exclusive-OR. L'autre entrée de cette deuxième porte OU exclusif est Y et produit une sortie de W ⊕ X ⊕ Y.
Générateur de parité impaire
Si un nombre pair de uns est présent dans l'entrée, alors le bit de parité impair, P doit être égal à «1» afin que le mot résultant contienne un nombre impair de uns. Pour les autres combinaisons d'entrée, bit de parité impair, P doit être égal à «0».
Suivez la même procédure du générateur de parité paire pour implémenter le générateur de parité impaire. lecircuit diagram du générateur de parité impaire est illustré dans la figure suivante.

Le schéma de circuit ci-dessus comprend une porte Ex-OR au premier niveau et une porte Ex-NOR au deuxième niveau. Puisque la parité impaire est juste opposée à la parité paire, nous pouvons placer un onduleur à la sortie du générateur de parité paire. Dans ce cas, les premier et deuxième niveaux contiennent une porte ExOR dans chaque niveau et le troisième niveau est constitué d'un inverseur.
Vérificateur de parité
Il existe deux types de vérificateurs de parité en fonction du type de parité à vérifier. Even parity checkervérifie l'erreur dans les données transmises, qui contiennent des bits de message avec une parité paire. De même,odd parity checker vérifie l'erreur dans les données transmises, qui contient des bits de message avec une parité impaire.
Vérificateur de parité paire
Maintenant, implémentons un circuit de contrôle de parité pair. Supposons une entrée binaire de 3 bits, WXY est transmis avec un bit de parité paire, P. Ainsi, le mot résultant (données) contient 4 bits, qui seront reçus comme entrée du vérificateur de parité paire.
Il génère un even parity check bit, E. Ce bit sera nul, si les données reçues en contiennent un nombre pair. Cela signifie qu'il n'y a pas d'erreur dans les données reçues. Ce bit de contrôle de parité paire sera un, si les données reçues en contiennent un nombre impair. Cela signifie qu'il y a une erreur dans les données reçues.
Le tableau suivant montre les Truth table d'un vérificateur de parité pair.
| Données reçues 4 bits WXYP | Contrôle de parité paire bit E |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 1 |
| 0011 | 0 |
| 0100 | 1 |
| 0101 | 0 |
| 0110 | 0 |
| 0111 | 1 |
| 1000 | 1 |
| 1001 | 0 |
| 1010 | 0 |
| 1011 | 1 |
| 1100 | 0 |
| 1101 | 1 |
| 1110 | 1 |
| 1111 | 0 |
À partir de la table de vérité ci-dessus, nous pouvons observer que la valeur du bit de contrôle de parité paire est «1», lorsqu'un nombre impair de ceux est présent dans les données reçues. Cela signifie que la fonction booléenne du bit de contrôle de parité paire est unodd function. La fonction OU exclusif satisfait cette condition. Par conséquent, nous pouvons directement écrire leBoolean function du bit de contrôle de parité pair comme
$$E=W \oplus X \oplus Y \oplus P$$
La figure suivante montre le circuit diagram du vérificateur de parité pair.

Ce circuit se compose de trois Exclusive-OR gatesayant deux entrées chacun. Les portes de premier niveau produisent des sorties de$W \oplus X$ & $Y \oplus P$. La porte OU exclusif, qui est au deuxième niveau, produit une sortie de$W \oplus X \oplus Y \oplus P$
Vérificateur de parité impaire
Supposons une entrée binaire à 3 bits, WXY est transmis avec le bit de parité impaire, P. Ainsi, le mot résultant (données) contient 4 bits, qui seront reçus comme entrée du vérificateur de parité impaire.
Il génère un odd parity check bit, E. Ce bit sera nul, si les données reçues contiennent un nombre impair de uns. Cela signifie qu'il n'y a pas d'erreur dans les données reçues. Ce bit de contrôle de parité impair sera un, si les données reçues en contiennent un nombre pair. Cela signifie qu'il y a une erreur dans les données reçues.
Suivez la même procédure qu'un vérificateur de parité paire pour implémenter un vérificateur de parité impaire. lecircuit diagram du vérificateur de parité impaire est illustré dans la figure suivante.

Le schéma de circuit ci-dessus comprend des portes Ex-OR au premier niveau et une porte Ex-NOR au deuxième niveau. Puisque la parité impaire est juste opposée à la parité paire, nous pouvons placer un inverseur à la sortie du vérificateur de parité paire. Dans ce cas, les premier, deuxième et troisième niveaux contiennent respectivement deux portes Ex-OR, une porte Ex-OR et un inverseur.
Additionneur binaire
L'opération arithmétique la plus élémentaire est l'addition. Le circuit, qui effectue l'addition de deux nombres binaires est connu commeBinary adder. Tout d'abord, implémentons un additionneur, qui effectue l'addition de deux bits.
Demi-additionneur
Le demi-additionneur est un circuit combinatoire, qui effectue l'addition de deux nombres binaires A et B sont de single bit. Il produit deux sorties sum, S & carry, C.
le Truth table du demi-additionneur est montré ci-dessous.
| Contributions | Les sorties | ||
|---|---|---|---|
| UNE | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Lorsque nous ajoutons deux bits, la somme résultante peut avoir des valeurs allant de 0 à 2 en décimal. Nous pouvons représenter les chiffres décimaux 0 et 1 avec un seul bit en binaire. Mais, nous ne pouvons pas représenter le chiffre décimal 2 avec un seul bit en binaire. Donc, nous avons besoin de deux bits pour le représenter en binaire.
Soit, somme, S est le bit le moins significatif et reporté, C est le bit le plus significatif de la somme résultante. Pour les trois premières combinaisons d'entrées, report, C est zéro et la valeur de S sera soit zéro soit un en fonction dunumber of onesprésent aux entrées. Mais, pour la dernière combinaison d'entrées, report, C est un et somme, S est zéro, puisque la somme résultante est de deux.
À partir de la table de vérité, nous pouvons directement écrire le Boolean functions pour chaque sortie comme
$$S=A \oplus B$$
$C=AB$
Nous pouvons implémenter les fonctions ci-dessus avec une porte Ex-OR à 2 entrées et une porte ET à 2 entrées. lecircuit diagram du demi-additionneur est montré dans la figure suivante.

Dans le circuit ci-dessus, une porte Ex-OU à deux entrées et une porte ET à deux entrées produisent respectivement la somme, S & retenue, C. Par conséquent, Half-additionner effectue l'addition de deux bits.
Additionneur complet
L'additionneur complet est un circuit combinatoire, qui effectue le addition of three bitsA, B et C dans . Où, A et B sont les deux bits significatifs parallèles et C in est le bit de retenue, qui est généré à partir de l'étape précédente. Cet additionneur complet produit également deux sorties sum, S & carry, C out , qui sont similaires à Half additionner.
le Truth table de l'additionneur complet est montré ci-dessous.
| Contributions | Les sorties | |||
|---|---|---|---|---|
| A | B | Cin | Cout | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Lorsque nous ajoutons trois bits, la somme résultante peut avoir des valeurs allant de 0 à 3 en décimal. Nous pouvons représenter les chiffres décimaux 0 et 1 avec un seul bit en binaire. Mais, nous ne pouvons pas représenter les chiffres décimaux 2 et 3 avec un seul bit en binaire. Donc, nous avons besoin de deux bits pour représenter ces deux chiffres décimaux en binaire.
Soit, somme, S est le bit le moins significatif et reporté, C out est le bit le plus significatif de la somme résultante. Il est facile de renseigner les valeurs des sorties pour toutes les combinaisons d'entrées dans la table de vérité. Il suffit de compter lenumber of onesprésent aux entrées et écrire le nombre binaire équivalent aux sorties. Si C in est égal à zéro, alors la table de vérité de l'additionneur complet est la même que celle de la table de vérité du demi-additionneur.
Nous obtiendrons ce qui suit Boolean functions pour chaque sortie après simplification.
$$S=A \oplus B \oplus C_{in}$$
$c_{out} = AB + \left ( A \oplus B \right )c_{in}$
La somme, S est égale à un, lorsqu'un nombre impair de uns est présent aux entrées. Nous savons que la porte Ex-OR produit une sortie, qui est une fonction impaire. Ainsi, nous pouvons utiliser deux portes Ex-OR à 2 entrées ou une porte Ex-OR à 3 entrées afin de produire la somme, S. Nous pouvons implémenter le report, C out en utilisant deux portes ET à 2 entrées et une porte OU. lecircuit diagram de l'additionneur complet est illustré dans la figure suivante.
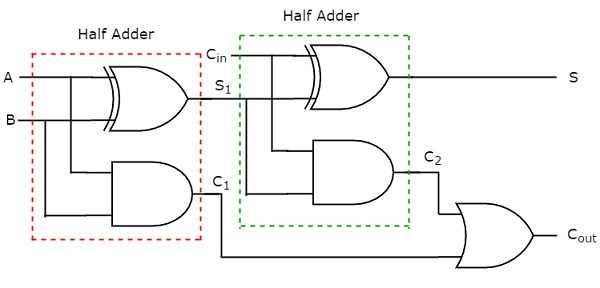
Cet additionneur est appelé comme Full addercar pour implémenter un additionneur complet, nous avons besoin de deux additionneurs Half et d'une porte OU. Si C in est égal à zéro, alors l'additionneur complet devient Demi additionneur. Nous pouvons le vérifier facilement à partir du schéma ci-dessus ou à partir des fonctions booléennes des sorties de l'additionneur complet.
Additionneur binaire 4 bits
L'additionneur binaire 4 bits effectue le addition of two 4-bit numbers. Laissez les nombres binaires de 4 bits,$A=A_{3}A_{2}A_{1}A_{0}$ et $B= B_{3}B_{2}B_{1}B_{0}$. Nous pouvons implémenter un additionneur binaire 4 bits de l'une des deux manières suivantes.
Utilisez un demi-additionneur pour ajouter deux bits les moins significatifs et trois additionneurs complets pour ajouter trois bits de poids plus élevé.
Utilisez quatre additionneurs complets pour l'uniformité. Puisque, le report initial C in est égal à zéro, l'additionneur complet qui est utilisé pour ajouter les bits les moins significatifs devient l'additionneur demi.
Pour le moment, nous avons envisagé une deuxième approche. leblock diagram de l'additionneur binaire 4 bits est illustré dans la figure suivante.

Ici, les 4 additionneurs complets sont en cascade. Chaque additionneur complet obtient les bits respectifs de deux entrées parallèles A et B. La sortie de retenue d'un additionneur complet sera l'entrée de retenue de l'additionneur complet d'ordre supérieur suivant. Cet additionneur binaire de 4 bits produit la somme résultante ayant au plus 5 bits. Donc, effectuer de la dernière étape L'additionneur complet sera le MSB.
De cette façon, nous pouvons implémenter n'importe quel additionneur binaire d'ordre supérieur simplement en cascadant le nombre requis d'additionneurs complets. Cet additionneur binaire est également appeléripple carry (binary) adder parce que le report se propage (ondulations) d'une étape à l'autre.
Soustracteur binaire
Le circuit, qui effectue la soustraction de deux nombres binaires est connu comme Binary subtractor. Nous pouvons implémenter le soustracteur binaire en suivant deux méthodes.
- Soustracteurs complets en cascade
- Méthode du complément de 2
Dans la première méthode, nous obtiendrons un soustracteur binaire de n bits en cascadant des soustracteurs complets 'n'. Ainsi, vous pouvez d'abord implémenter Half soustractor et Full soustractor, similaires à Half additionner & Full additionneur. Ensuite, vous pouvez implémenter un soustracteur binaire de n bits, en cascadant des soustracteurs complets 'n'. Ainsi, nous aurons deux circuits séparés pour l'addition et la soustraction binaires de deux nombres binaires.
Dans la deuxième méthode, nous pouvons utiliser le même additionneur binaire pour soustraire deux nombres binaires simplement en faisant quelques modifications dans la deuxième entrée. Ainsi, une opération d'addition binaire interne a lieu, mais la sortie est une soustraction résultante.
Nous savons que la soustraction de deux nombres binaires A et B peut s'écrire,
$$A-B = A+\left ( {2}'s \: compliment \: of \: B \right )$$
$\Rightarrow A-B = A+\left ( {1}'s \: compliment \: of \: B \right )+1$
Soustracteur binaire 4 bits
Le soustracteur binaire 4 bits produit le subtraction of two 4-bit numbers. Laissez les nombres binaires 4 bits,$A=A_{3}A_{2}A_{1}A_{0}$ et $B= B_{3}B_{2}B_{1}B_{0}$. En interne, le fonctionnement du soustracteur binaire 4 bits est similaire à celui de l'additionneur binaire 4 bits. Si les bits normaux du nombre binaire A, les bits complétés du nombre binaire B et le report initial (emprunter), C in as one sont appliqués à l'additionneur binaire de 4 bits, alors il devient un soustracteur binaire de 4 bits. leblock diagram du soustracteur binaire 4 bits est illustré dans la figure suivante.

Ce soustracteur binaire de 4 bits produit une sortie, qui a au plus 5 bits. Si le nombre binaire A est supérieur au nombre binaire B, alors MSB de la sortie est égal à zéro et les bits restants contiennent la grandeur de AB. Si le nombre binaire A est inférieur au nombre binaire B, alors MSB de la sortie est un. Alors, prenez le complément 2 de la sortie afin d'obtenir la magnitude de AB.
In this way, we can implement any higher order binary subtractor just by cascading the required number of Full adders with necessary modifications.
Binary Adder / Subtractor
The circuit, which can be used to perform either addition or subtraction of two binary numbers at any time is known as Binary Adder / subtractor. Both, Binary adder and Binary subtractor contain a set of Full adders, which are cascaded. The input bits of binary number A are directly applied in both Binary adder and Binary subtractor.
There are two differences in the inputs of Full adders that are present in Binary adder and Binary subtractor.
The input bits of binary number B are directly applied to Full adders in Binary adder, whereas the complemented bits of binary number B are applied to Full adders in Binary subtractor.
The initial carry, C0 = 0 is applied in 4-bit Binary adder, whereas the initial carry (borrow), C0 = 1 is applied in 4-bit Binary subtractor.
We know that a 2-input Ex-OR gate produces an output, which is same as that of first input when other input is zero. Similarly, it produces an output, which is complement of first input when other input is one.
Therefore, we can apply the input bits of binary number B, to 2-input Ex-OR gates. The other input to all these Ex-OR gates is C0. So, based on the value of C0, the Ex-OR gates produce either the normal or complemented bits of binary number B.
4-bit Binary Adder / Subtractor
The 4-bit binary adder / subtractor produces either the addition or the subtraction of two 4-bit numbers based on the value of initial carry or borrow, 0. Let the 4-bit binary numbers, $A=A_{3}A_{2}A_{1}A_{0}$ and $B= B_{3}B_{2}B_{1}B_{0}$. The operation of 4-bit Binary adder / subtractor is similar to that of 4-bit Binary adder and 4-bit Binary subtractor.
Apply the normal bits of binary numbers A and B & initial carry or borrow, C0 from externally to a 4-bit binary adder. The block diagram of 4-bit binary adder / subtractor is shown in the following figure.
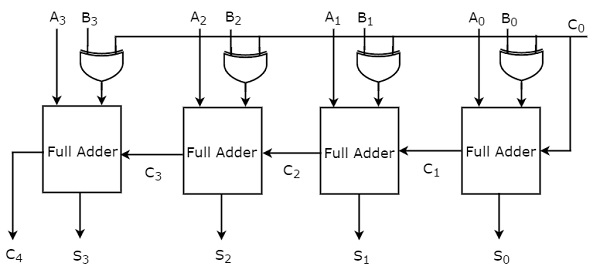
If initial carry, 0 is zero, then each full adder gets the normal bits of binary numbers A & B. So, the 4-bit binary adder / subtractor produces an output, which is the addition of two binary numbers A & B.
If initial borrow, 0 is one, then each full adder gets the normal bits of binary number A & complemented bits of binary number B. So, the 4-bit binary adder / subtractor produces an output, which is the subtraction of two binary numbers A & B.
Therefore, with the help of additional Ex-OR gates, the same circuit can be used for both addition and subtraction of two binary numbers.
Decoder is a combinational circuit that has ‘n’ input lines and maximum of 2n output lines. One of these outputs will be active High based on the combination of inputs present, when the decoder is enabled. That means decoder detects a particular code. The outputs of the decoder are nothing but the min terms of ‘n’ input variables (lines), when it is enabled.
2 to 4 Decoder
Let 2 to 4 Decoder has two inputs A1 & A0 and four outputs Y3, Y2, Y1 & Y0. The block diagram of 2 to 4 decoder is shown in the following figure.

One of these four outputs will be ‘1’ for each combination of inputs when enable, E is ‘1’. The Truth table of 2 to 4 decoder is shown below.
| Enable | Inputs | Outputs | ||||
|---|---|---|---|---|---|---|
| E | A1 | A0 | Y3 | Y2 | Y1 | Y0 |
| 0 | x | x | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
From Truth table, we can write the Boolean functions for each output as
$$Y_{3}=E.A_{1}.A_{0}$$
$$ Y_{2}=E.A_{1}.{A_{0}}'$$
$$ Y_{1}=E.{A_{1}}'.A_{0}$$
$$ Y_{0}=E.{A_{1}}'.{A_{0}}'$$
Each output is having one product term. So, there are four product terms in total. We can implement these four product terms by using four AND gates having three inputs each & two inverters. The circuit diagram of 2 to 4 decoder is shown in the following figure.

Therefore, the outputs of 2 to 4 decoder are nothing but the min terms of two input variables A1 & A0, when enable, E is equal to one. If enable, E is zero, then all the outputs of decoder will be equal to zero.
Similarly, 3 to 8 decoder produces eight min terms of three input variables A2, A1 & A0 and 4 to 16 decoder produces sixteen min terms of four input variables A3, A2, A1 & A0.
Implementation of Higher-order Decoders
Now, let us implement the following two higher-order decoders using lower-order decoders.
- 3 to 8 decoder
- 4 to 16 decoder
3 to 8 Decoder
In this section, let us implement 3 to 8 decoder using 2 to 4 decoders. We know that 2 to 4 Decoder has two inputs, A1 & A0 and four outputs, Y3 to Y0. Whereas, 3 to 8 Decoder has three inputs A2, A1 & A0 and eight outputs, Y7 to Y0.
We can find the number of lower order decoders required for implementing higher order decoder using the following formula.
$$Required \: number \: of \: lower \: order \: decoders=\frac{m_{2}}{m_{1}}$$
Where,
$m_{1}$ is the number of outputs of lower order decoder.
$m_{2}$ is the number of outputs of higher order decoder.
Here, $m_{1}$ = 4 and $m_{2}$ = 8. Substitute, these two values in the above formula.
$$Required \: number \: of \: 2 \: to \: 4 \: decoders=\frac{8}{4}=2$$
Therefore, we require two 2 to 4 decoders for implementing one 3 to 8 decoder. The block diagram of 3 to 8 decoder using 2 to 4 decoders is shown in the following figure.

The parallel inputs A1 & A0 are applied to each 2 to 4 decoder. The complement of input A2 is connected to Enable, E of lower 2 to 4 decoder in order to get the outputs, Y3 to Y0. These are the lower four min terms. The input, A2 is directly connected to Enable, E of upper 2 to 4 decoder in order to get the outputs, Y7 to Y4. These are the higher four min terms.
4 to 16 Decoder
In this section, let us implement 4 to 16 decoder using 3 to 8 decoders. We know that 3 to 8 Decoder has three inputs A2, A1 & A0 and eight outputs, Y7 to Y0. Whereas, 4 to 16 Decoder has four inputs A3, A2, A1 & A0 and sixteen outputs, Y15 to Y0
We know the following formula for finding the number of lower order decoders required.
$$Required \: number \: of \: lower \: order \: decoders=\frac{m_{2}}{m_{1}}$$
Substitute, $m_{1}$ = 8 and $m_{2}$ = 16 in the above formula.
$$Required \: number \: of \: 3 \: to \: 8 decoders=\frac{16}{8}=2$$
Therefore, we require two 3 to 8 decoders for implementing one 4 to 16 decoder. The block diagram of 4 to 16 decoder using 3 to 8 decoders is shown in the following figure.

The parallel inputs A2, A1 & A0 are applied to each 3 to 8 decoder. The complement of input, A3 is connected to Enable, E of lower 3 to 8 decoder in order to get the outputs, Y7 to Y0. These are the lower eight min terms. The input, A3 is directly connected to Enable, E of upper 3 to 8 decoder in order to get the outputs, Y15 to Y8. These are the higher eight min terms.
An Encoder is a combinational circuit that performs the reverse operation of Decoder. It has maximum of 2n input lines and ‘n’ output lines. It will produce a binary code equivalent to the input, which is active High. Therefore, the encoder encodes 2n input lines with ‘n’ bits. It is optional to represent the enable signal in encoders.
4 to 2 Encoder
Let 4 to 2 Encoder has four inputs Y3, Y2, Y1 & Y0 and two outputs A1 & A0. The block diagram of 4 to 2 Encoder is shown in the following figure.

At any time, only one of these 4 inputs can be ‘1’ in order to get the respective binary code at the output. The Truth table of 4 to 2 encoder is shown below.
| Inputs | Outputs | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
From Truth table, we can write the Boolean functions for each output as
$$A_{1}=Y_{3}+Y_{2}$$
$$A_{0}=Y_{3}+Y_{1}$$
We can implement the above two Boolean functions by using two input OR gates. The circuit diagram of 4 to 2 encoder is shown in the following figure.

The above circuit diagram contains two OR gates. These OR gates encode the four inputs with two bits
Octal to Binary Encoder
Octal to binary Encoder has eight inputs, Y7 to Y0 and three outputs A2, A1 & A0. Octal to binary encoder is nothing but 8 to 3 encoder. The block diagram of octal to binary Encoder is shown in the following figure.
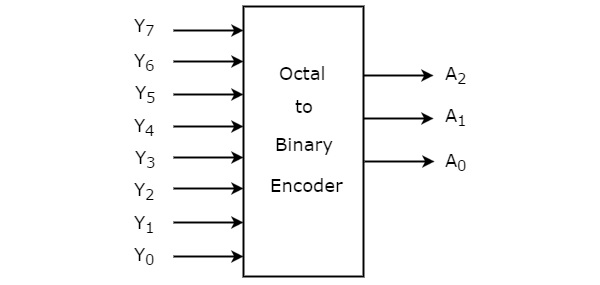
At any time, only one of these eight inputs can be ‘1’ in order to get the respective binary code. The Truth table of octal to binary encoder is shown below.
| Inputs | Outputs | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
From Truth table, we can write the Boolean functions for each output as
$$A_{2}=Y_{7}+Y_{6}+Y_{5}+Y_{4}$$
$$A_{1}=Y_{7}+Y_{6}+Y_{3}+Y_{2}$$
$$A_{0}=Y_{7}+Y_{5}+Y_{3}+Y_{1}$$
We can implement the above Boolean functions by using four input OR gates. The circuit diagram of octal to binary encoder is shown in the following figure.

The above circuit diagram contains three 4-input OR gates. These OR gates encode the eight inputs with three bits.
Drawbacks of Encoder
Following are the drawbacks of normal encoder.
There is an ambiguity, when all outputs of encoder are equal to zero. Because, it could be the code corresponding to the inputs, when only least significant input is one or when all inputs are zero.
If more than one input is active High, then the encoder produces an output, which may not be the correct code. For example, if both Y3 and Y6 are ‘1’, then the encoder produces 111 at the output. This is neither equivalent code corresponding to Y3, when it is ‘1’ nor the equivalent code corresponding to Y6, when it is ‘1’.
So, to overcome these difficulties, we should assign priorities to each input of encoder. Then, the output of encoder will be the (binary) code corresponding to the active High input(s), which has higher priority. This encoder is called as priority encoder.
Priority Encoder
A 4 to 2 priority encoder has four inputs Y3, Y2, Y1 & Y0 and two outputs A1 & A0. Here, the input, Y3 has the highest priority, whereas the input, Y0 has the lowest priority. In this case, even if more than one input is ‘1’ at the same time, the output will be the (binary) code corresponding to the input, which is having higher priority.
We considered one more output, V in order to know, whether the code available at outputs is valid or not.
If at least one input of the encoder is ‘1’, then the code available at outputs is a valid one. In this case, the output, V will be equal to 1.
If all the inputs of encoder are ‘0’, then the code available at outputs is not a valid one. In this case, the output, V will be equal to 0.
The Truth table of 4 to 2 priority encoder is shown below.
| Inputs | Outputs | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | V |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | x | 0 | 1 | 1 |
| 0 | 1 | x | x | 1 | 0 | 1 |
| 1 | x | x | x | 1 | 1 | 1 |
Use 4 variable K-maps for getting simplified expressions for each output.
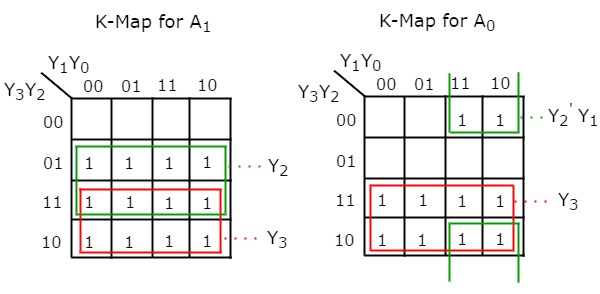
The simplified Boolean functions are
$$A_{1}=Y_{3}+Y_{2}$$
$A_{0}=Y_{3}+{Y_{2}}'Y_{1}$
Similarly, we will get the Boolean function of output, V as
$$V=Y_{3}+Y_{2}+Y_{1}+Y_{0}$$
We can implement the above Boolean functions using logic gates. The circuit diagram of 4 to 2 priority encoder is shown in the following figure.

The above circuit diagram contains two 2-input OR gates, one 4-input OR gate, one 2input AND gate & an inverter. Here AND gate & inverter combination are used for producing a valid code at the outputs, even when multiple inputs are equal to ‘1’ at the same time. Hence, this circuit encodes the four inputs with two bits based on the priority assigned to each input.
Multiplexer is a combinational circuit that has maximum of 2n data inputs, ‘n’ selection lines and single output line. One of these data inputs will be connected to the output based on the values of selection lines.
Since there are ‘n’ selection lines, there will be 2n possible combinations of zeros and ones. So, each combination will select only one data input. Multiplexer is also called as Mux.
4x1 Multiplexer
4x1 Multiplexer has four data inputs I3, I2, I1 & I0, two selection lines s1 & s0 and one output Y. The block diagram of 4x1 Multiplexer is shown in the following figure.

One of these 4 inputs will be connected to the output based on the combination of inputs present at these two selection lines. Truth table of 4x1 Multiplexer is shown below.
| Selection Lines | Output | |
|---|---|---|
| S1 | S0 | Y |
| 0 | 0 | I0 |
| 0 | 1 | I1 |
| 1 | 0 | I2 |
| 1 | 1 | I3 |
From Truth table, we can directly write the Boolean function for output, Y as
$$Y={S_{1}}'{S_{0}}'I_{0}+{S_{1}}'S_{0}I_{1}+S_{1}{S_{0}}'I_{2}+S_{1}S_{0}I_{3}$$
We can implement this Boolean function using Inverters, AND gates & OR gate. The circuit diagram of 4x1 multiplexer is shown in the following figure.

We can easily understand the operation of the above circuit. Similarly, you can implement 8x1 Multiplexer and 16x1 multiplexer by following the same procedure.
Implementation of Higher-order Multiplexers.
Now, let us implement the following two higher-order Multiplexers using lower-order Multiplexers.
- 8x1 Multiplexer
- 16x1 Multiplexer
8x1 Multiplexer
In this section, let us implement 8x1 Multiplexer using 4x1 Multiplexers and 2x1 Multiplexer. We know that 4x1 Multiplexer has 4 data inputs, 2 selection lines and one output. Whereas, 8x1 Multiplexer has 8 data inputs, 3 selection lines and one output.
So, we require two 4x1 Multiplexers in first stage in order to get the 8 data inputs. Since, each 4x1 Multiplexer produces one output, we require a 2x1 Multiplexer in second stage by considering the outputs of first stage as inputs and to produce the final output.
Let the 8x1 Multiplexer has eight data inputs I7 to I0, three selection lines s2, s1 & s0 and one output Y. The Truth table of 8x1 Multiplexer is shown below.
| Selection Inputs | Output | ||
|---|---|---|---|
| S2 | S1 | S0 | Y |
| 0 | 0 | 0 | I0 |
| 0 | 0 | 1 | I1 |
| 0 | 1 | 0 | I2 |
| 0 | 1 | 1 | I3 |
| 1 | 0 | 0 | I4 |
| 1 | 0 | 1 | I5 |
| 1 | 1 | 0 | I6 |
| 1 | 1 | 1 | I7 |
We can implement 8x1 Multiplexer using lower order Multiplexers easily by considering the above Truth table. The block diagram of 8x1 Multiplexer is shown in the following figure.

The same selection lines, s1 & s0 are applied to both 4x1 Multiplexers. The data inputs of upper 4x1 Multiplexer are I7 to I4 and the data inputs of lower 4x1 Multiplexer are I3 to I0. Therefore, each 4x1 Multiplexer produces an output based on the values of selection lines, s1 & s0.
The outputs of first stage 4x1 Multiplexers are applied as inputs of 2x1 Multiplexer that is present in second stage. The other selection line, s2 is applied to 2x1 Multiplexer.
If s2 is zero, then the output of 2x1 Multiplexer will be one of the 4 inputs I3 to I0 based on the values of selection lines s1 & s0.
If s2 is one, then the output of 2x1 Multiplexer will be one of the 4 inputs I7 to I4 based on the values of selection lines s1 & s0.
Therefore, the overall combination of two 4x1 Multiplexers and one 2x1 Multiplexer performs as one 8x1 Multiplexer.
16x1 Multiplexer
In this section, let us implement 16x1 Multiplexer using 8x1 Multiplexers and 2x1 Multiplexer. We know that 8x1 Multiplexer has 8 data inputs, 3 selection lines and one output. Whereas, 16x1 Multiplexer has 16 data inputs, 4 selection lines and one output.
So, we require two 8x1 Multiplexers in first stage in order to get the 16 data inputs. Since, each 8x1 Multiplexer produces one output, we require a 2x1 Multiplexer in second stage by considering the outputs of first stage as inputs and to produce the final output.
Let the 16x1 Multiplexer has sixteen data inputs I15 to I0, four selection lines s3 to s0 and one output Y. The Truth table of 16x1 Multiplexer is shown below.
| Selection Inputs | Output | |||
|---|---|---|---|---|
| S3 | S2 | S1 | S0 | Y |
| 0 | 0 | 0 | 0 | I0 |
| 0 | 0 | 0 | 1 | I1 |
| 0 | 0 | 1 | 0 | I2 |
| 0 | 0 | 1 | 1 | I3 |
| 0 | 1 | 0 | 0 | I4 |
| 0 | 1 | 0 | 1 | I5 |
| 0 | 1 | 1 | 0 | I6 |
| 0 | 1 | 1 | 1 | I7 |
| 1 | 0 | 0 | 0 | I8 |
| 1 | 0 | 0 | 1 | I9 |
| 1 | 0 | 1 | 0 | I10 |
| 1 | 0 | 1 | 1 | I11 |
| 1 | 1 | 0 | 0 | I12 |
| 1 | 1 | 0 | 1 | I13 |
| 1 | 1 | 1 | 0 | I14 |
| 1 | 1 | 1 | 1 | I15 |
We can implement 16x1 Multiplexer using lower order Multiplexers easily by considering the above Truth table. The block diagram of 16x1 Multiplexer is shown in the following figure.

The same selection lines, s2, s1 & s0 are applied to both 8x1 Multiplexers. The data inputs of upper 8x1 Multiplexer are I15 to I8 and the data inputs of lower 8x1 Multiplexer are I7 to I0. Therefore, each 8x1 Multiplexer produces an output based on the values of selection lines, s2, s1 & s0.
The outputs of first stage 8x1 Multiplexers are applied as inputs of 2x1 Multiplexer that is present in second stage. The other selection line, s3 is applied to 2x1 Multiplexer.
If s3 is zero, then the output of 2x1 Multiplexer will be one of the 8 inputs Is7 to I0 based on the values of selection lines s2, s1 & s0.
If s3 is one, then the output of 2x1 Multiplexer will be one of the 8 inputs I15 to I8 based on the values of selection lines s2, s1 & s0.
Therefore, the overall combination of two 8x1 Multiplexers and one 2x1 Multiplexer performs as one 16x1 Multiplexer.
De-Multiplexer is a combinational circuit that performs the reverse operation of Multiplexer. It has single input, ‘n’ selection lines and maximum of 2n outputs. The input will be connected to one of these outputs based on the values of selection lines.
Since there are ‘n’ selection lines, there will be 2n possible combinations of zeros and ones. So, each combination can select only one output. De-Multiplexer is also called as De-Mux.
1x4 De-Multiplexer
1x4 De-Multiplexer has one input I, two selection lines, s1 & s0 and four outputs Y3, Y2, Y1 &Y0. The block diagram of 1x4 De-Multiplexer is shown in the following figure.

The single input ‘I’ will be connected to one of the four outputs, Y3 to Y0 based on the values of selection lines s1 & s0. The Truth table of 1x4 De-Multiplexer is shown below.
| Selection Inputs | Outputs | ||||
|---|---|---|---|---|---|
| S1 | S0 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | I |
| 0 | 1 | 0 | 0 | I | 0 |
| 1 | 0 | 0 | I | 0 | 0 |
| 1 | 1 | I | 0 | 0 | 0 |
From the above Truth table, we can directly write the Boolean functions for each output as
$$Y_{3}=s_{1}s_{0}I$$
$$Y_{2}=s_{1}{s_{0}}'I$$
$$Y_{1}={s_{1}}'s_{0}I$$
$$Y_{0}={s_1}'{s_{0}}'I$$
We can implement these Boolean functions using Inverters & 3-input AND gates. The circuit diagram of 1x4 De-Multiplexer is shown in the following figure.

We can easily understand the operation of the above circuit. Similarly, you can implement 1x8 De-Multiplexer and 1x16 De-Multiplexer by following the same procedure.
Implementation of Higher-order De-Multiplexers
Now, let us implement the following two higher-order De-Multiplexers using lower-order De-Multiplexers.
- 1x8 De-Multiplexer
- 1x16 De-Multiplexer
1x8 De-Multiplexer
In this section, let us implement 1x8 De-Multiplexer using 1x4 De-Multiplexers and 1x2 De-Multiplexer. We know that 1x4 De-Multiplexer has single input, two selection lines and four outputs. Whereas, 1x8 De-Multiplexer has single input, three selection lines and eight outputs.
So, we require two 1x4 De-Multiplexers in second stage in order to get the final eight outputs. Since, the number of inputs in second stage is two, we require 1x2 DeMultiplexer in first stage so that the outputs of first stage will be the inputs of second stage. Input of this 1x2 De-Multiplexer will be the overall input of 1x8 De-Multiplexer.
Let the 1x8 De-Multiplexer has one input I, three selection lines s2, s1 & s0 and outputs Y7 to Y0. The Truth table of 1x8 De-Multiplexer is shown below.
| Selection Inputs | Outputs | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| s2 | s1 | s0 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | I | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
We can implement 1x8 De-Multiplexer using lower order Multiplexers easily by considering the above Truth table. The block diagram of 1x8 De-Multiplexer is shown in the following figure.

The common selection lines, s1 & s0 are applied to both 1x4 De-Multiplexers. The outputs of upper 1x4 De-Multiplexer are Y7 to Y4 and the outputs of lower 1x4 De-Multiplexer are Y3 to Y0.
The other selection line, s2 is applied to 1x2 De-Multiplexer. If s2 is zero, then one of the four outputs of lower 1x4 De-Multiplexer will be equal to input, I based on the values of selection lines s1 & s0. Similarly, if s2 is one, then one of the four outputs of upper 1x4 DeMultiplexer will be equal to input, I based on the values of selection lines s1 & s0.
1x16 De-Multiplexer
In this section, let us implement 1x16 De-Multiplexer using 1x8 De-Multiplexers and 1x2 De-Multiplexer. We know that 1x8 De-Multiplexer has single input, three selection lines and eight outputs. Whereas, 1x16 De-Multiplexer has single input, four selection lines and sixteen outputs.
So, we require two 1x8 De-Multiplexers in second stage in order to get the final sixteen outputs. Since, the number of inputs in second stage is two, we require 1x2 DeMultiplexer in first stage so that the outputs of first stage will be the inputs of second stage. Input of this 1x2 De-Multiplexer will be the overall input of 1x16 De-Multiplexer.
Let the 1x16 De-Multiplexer has one input I, four selection lines s3, s2, s1 & s0 and outputs Y15 to Y0. The block diagram of 1x16 De-Multiplexer using lower order Multiplexers is shown in the following figure.
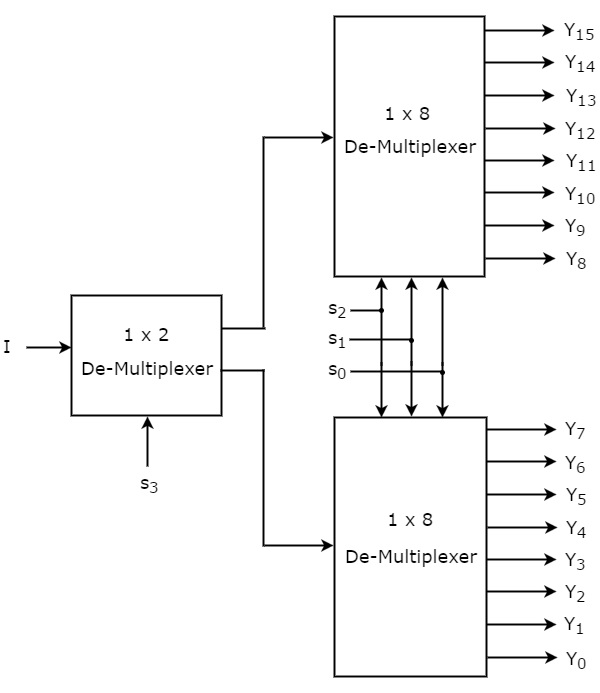
The common selection lines s2, s1 & s0 are applied to both 1x8 De-Multiplexers. The outputs of upper 1x8 De-Multiplexer are Y15 to Y8 and the outputs of lower 1x8 DeMultiplexer are Y7 to Y0.
L'autre selection line, s3est appliqué au De-Multiplexer 1x2. Si s 3 est égal à zéro, alors l'une des huit sorties du De-Multiplexer 1x8 inférieur sera égale à l'entrée, I basée sur les valeurs des lignes de sélection s 2 , s 1 et s 0 . De même, si s3 est un, alors l'une des 8 sorties du De-Multiplexer 1x8 supérieur sera égale à l'entrée, I basée sur les valeurs des lignes de sélection s 2 , s 1 et s 0 .
Dispositifs logiques programmables (PLDs)sont les circuits intégrés. Ils contiennent un tableau de portes ET et un autre tableau de portes OU. Il existe trois types de PLD basés sur le type de tableau (s), qui ont une fonction programmable.
- Mémoire morte programmable
- Logique de matrice programmable
- Réseau logique programmable
Le processus de saisie des informations dans ces appareils est appelé programming. Fondamentalement, les utilisateurs peuvent programmer ces dispositifs ou CI électriquement afin d'implémenter les fonctions booléennes en fonction de l'exigence. Ici, le terme programmation fait référence à la programmation matérielle mais pas à la programmation logicielle.
Mémoire morte programmable (PROM)
La mémoire morte (ROM) est un périphérique de mémoire, qui stocke les informations binaires en permanence. Cela signifie que nous ne pouvons pas modifier ces informations stockées par la suite. Si la ROM a une fonction programmable, elle est appelée commeProgrammable ROM (PROM). L'utilisateur a la possibilité de programmer les informations binaires électriquement une fois en utilisant le programmeur PROM.
PROM est un dispositif logique programmable qui a une matrice ET fixe et une matrice OU programmable. leblock diagram de PROM est illustré dans la figure suivante.

Ici, les entrées des portes ET ne sont pas de type programmable. Nous devons donc générer 2 n termes de produit en utilisant 2 n portes ET ayant chacune n entrées. Nous pouvons implémenter ces termes produit en utilisant le décodeur nx2 n . Donc, ce décodeur génère 'n'min terms.
Ici, les entrées des portes OU sont programmables. Cela signifie que nous pouvons programmer n'importe quel nombre de termes de produit requis, puisque toutes les sorties des portes ET sont appliquées en tant qu'entrées à chaque porte OU. Par conséquent, les résultats de PROM seront sous la forme desum of min terms.
Exemple
Laissez-nous mettre en œuvre ce qui suit Boolean functions en utilisant PROM.
$$A(X,Y,Z)=\sum m\left ( 5,6,7 \right )$$
$$B(X,Y,Z)=\sum m\left ( 3,5,6,7 \right )$$
Les deux fonctions données sont sous forme de somme de termes min et chaque fonction a trois variables X, Y et Z. Donc, nous avons besoin d'un décodeur 3 à 8 et de deux portes OU programmables pour produire ces deux fonctions. Le correspondantPROM est illustré dans la figure suivante.

Ici, 3 à 8 décodeurs génèrent huit termes min. Les deux portes OU programmables ont accès à tous ces termes minimum. Mais, seuls les termes minimum requis sont programmés afin de produire les fonctions booléennes respectives par chaque porte OU. Le symbole «X» est utilisé pour les connexions programmables.
Logique de matrice programmable (PAL)
PAL est un dispositif logique programmable doté d'une matrice ET programmable et d'une matrice OU fixe. L'avantage de PAL est que nous pouvons générer uniquement les termes de produit requis de la fonction booléenne au lieu de générer tous les termes minimum en utilisant des portes ET programmables. leblock diagram de PAL est illustré dans la figure suivante.

Ici, les entrées des portes ET sont programmables. Cela signifie que chaque porte ET a des entrées de variables normales et complémentaires. Ainsi, en fonction de l'exigence, nous pouvons programmer n'importe laquelle de ces entrées. Ainsi, nous ne pouvons générer que lesproduct terms en utilisant ces portes ET.
Ici, les entrées des portes OU ne sont pas de type programmable. Ainsi, le nombre d'entrées de chaque porte OU sera de type fixe. Par conséquent, appliquez ces conditions de produit requises à chaque porte OU en tant qu'entrées. Par conséquent, les sorties de PAL seront sous la forme desum of products form.
Exemple
Laissez-nous mettre en œuvre ce qui suit Boolean functions en utilisant PAL.
$$A=XY+X{Z}'$$
$$A=X{Y}'+Y{Z}'$$
Les deux fonctions données sont sous forme de somme de produits. Il existe deux termes de produit présents dans chaque fonction booléenne. Nous avons donc besoin de quatre portes ET programmables et de deux portes OU fixes pour produire ces deux fonctions. Le correspondantPAL est illustré dans la figure suivante.

le programmable AND gatesont accès aux entrées de variables normales et complétées. Dans la figure ci-dessus, les entrées X,${X}'$, Y, ${Y}'$, Z et ${Z}'$, sont disponibles aux entrées de chaque porte ET. Donc, programmez uniquement les littéraux requis afin de générer un terme de produit par chaque porte ET. Le symbole «X» est utilisé pour les connexions programmables.
Ici, les entrées des portes OU sont de type fixe. Ainsi, les termes de produit nécessaires sont connectés aux entrées de chaqueOR gate. Pour que les portes OU produisent les fonctions booléennes respectives. Le symbole '.' est utilisé pour les connexions fixes.
Réseau logique programmable (PLA)
PLA est un dispositif logique programmable qui a à la fois un tableau ET programmable et un tableau OU programmable. C'est donc le PLD le plus flexible. leblock diagram du PLA est illustré dans la figure suivante.

Ici, les entrées des portes ET sont programmables. Cela signifie que chaque porte ET a des entrées de variables normales et complémentaires. Ainsi, en fonction de l'exigence, nous pouvons programmer n'importe laquelle de ces entrées. Ainsi, nous ne pouvons générer que lesproduct terms en utilisant ces portes ET.
Ici, les entrées des portes OU sont également programmables. Ainsi, nous pouvons programmer n'importe quel nombre de termes de produit requis, puisque toutes les sorties des portes ET sont appliquées comme entrées à chaque porte OU. Par conséquent, les sorties de PAL seront sous la forme desum of products form.
Exemple
Laissez-nous mettre en œuvre ce qui suit Boolean functions en utilisant PLA.
$$A=XY+X{Z}'$$
$$B=X{Y}'+YZ+X{Z}'$$
Les deux fonctions données sont sous forme de somme de produits. Le nombre de termes de produit présents dans les fonctions booléennes A et B données est de deux et trois respectivement. Un terme de produit,${Z}'X$ est commun dans chaque fonction.
Nous avons donc besoin de quatre portes ET programmables et de deux portes OU programmables pour produire ces deux fonctions. Le correspondantPLA est illustré dans la figure suivante.
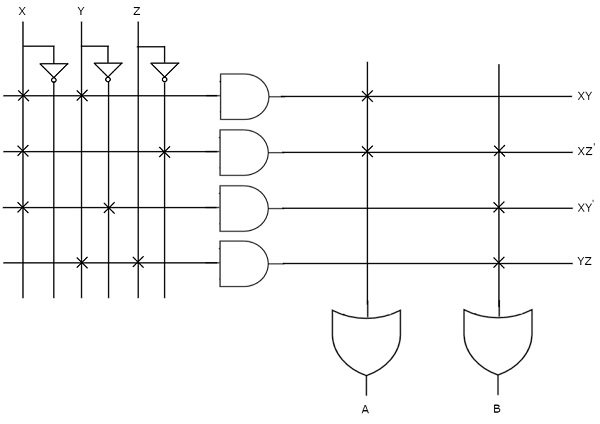
le programmable AND gatesont accès aux entrées de variables normales et complétées. Dans la figure ci-dessus, les entrées X,${X}'$, Y, ${Y}'$, Z et ${Z}'$, sont disponibles aux entrées de chaque porte ET. Donc, programmez uniquement les littéraux requis afin de générer un terme de produit par chaque porte ET.
Tous ces termes produits sont disponibles aux entrées de chaque programmable OR gate. Mais, programmez uniquement les termes du produit requis afin de produire les fonctions booléennes respectives par chaque porte OU. Le symbole «X» est utilisé pour les connexions programmables.
Dans les chapitres précédents, nous avons implémenté divers circuits combinatoires utilisant des portes logiques. À l'exception de la porte NOT, toutes les portes logiques restantes ont au moins deux entrées et une seule sortie. De même, lethreshold gate contient également au moins une entrée et une seule sortie.
De plus, il contient les poids respectifs de chaque entrée et une valeur de seuil. Les valeurs de ces poids et seuils pourraient être de n'importe quel nombre réel fini.
Principes de base de la porte de seuil
Soit les entrées de la porte de seuil sont X 1 , X 2 , X 3 ,…, X n . Les poids correspondants de ces entrées sont W 1 , W 2 , W 3 ,…, W n . lesymbol de seuil de seuil est illustré dans la figure suivante.
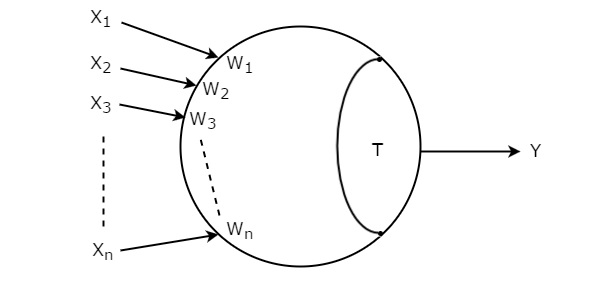
Threshold gateest représenté par un cercle et il a 'n' entrées, X 1 à X n et une seule sortie, Y. Ce cercle est composé de deux parties. Une partie représente les poids correspondant aux entrées et l'autre partie représente la valeur de seuil, T.
La somme des produits des intrants avec les poids correspondants est appelée weighted sum. Si cette somme pondérée est supérieure ou égale à la valeur de seuil, T alors seule la sortie, Y sera égale à un. Sinon, la sortie, Y sera égale à zéro.
Mathematically, nous pouvons écrire cette relation entre les entrées et la sortie de la porte de seuil comme ci-dessous.
$$Y=1, if \: \: W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{3}+...W_{n}X_{n}\geq T$$
= 0, sinon.
Par conséquent, nous pouvons implémenter diverses portes logiques et fonctions booléennes simplement en modifiant les valeurs des poids et / ou la valeur de seuil, T.
Exemple
Trouvons le simplified Boolean function pour la porte de seuil suivante.

Cette porte de seuil a trois entrées X 1 , X 2 , X 3 et une sortie Y.
Les poids correspondant aux entrées X 1 , X 2 et X 3 sont respectivement W 1 = 2, W 2 = 1 & W 3 = -4.
La valeur de la porte de seuil est T = -1.
le weighted sum de la porte de seuil est
$$W=W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{3}$$
Remplacez les poids donnés dans l'équation ci-dessus.
$$\Rightarrow W=2X_{1}+X_{2}-4X_{3}$$
Sortie de la porte de seuil, Y sera «1» si W ≥ −1, sinon ce sera «0».
Le suivant table montre la relation entre l'entrée et la sortie pour toutes les combinaisons possibles d'entrées.
| Contributions | Somme pondérée | Production | ||
|---|---|---|---|---|
| $X_{1}$ | $X_{2}$ | $X_{3}$ | $W=2X_{1}+X_{2}-4X_{3}$ | $Y$ |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | -4 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | -3 | 0 |
| 1 | 0 | 0 | 2 | 1 |
| 1 | 0 | 1 | -2 | 0 |
| 1 | 1 | 0 | 3 | 1 |
| 1 | 1 | 1 | -1 | 1 |
À partir du tableau ci-dessus, nous pouvons écrire le Boolean function pour la sortie, Y comme
$$Y= \sum m\left ( 0,2,4,6,7 \right )$$
La simplification de cette fonction booléenne en utilisant 3 variable K-Map est illustré dans la figure suivante.

Par conséquent, la simplified Boolean function pour une porte de seuil donnée est $Y={X_{3}'}+X_{1}X_{2}$.
Synthèse des fonctions de seuil
La porte de seuil est également appelée universal gateparce que nous pouvons implémenter n'importe quelle fonction booléenne en utilisant la (les) porte (s) de seuil. Parfois, il peut ne pas être possible d'implémenter quelques portes logiques et fonctions booléennes en utilisant une seule porte de seuil. Dans ce cas, nous pouvons avoir besoin de plusieurs portes de seuil.
Suivez ces steps pour implémenter une fonction booléenne en utilisant une seule porte de seuil.
Step 1 - Formuler un Truth table pour une fonction booléenne donnée.
Step 2 - Dans le tableau de vérité ci-dessus, ajoutez (incluez) une colonne supplémentaire, qui donne la relation entre weighted sums et Threshold value.
Step 3 - Écrivez la relation entre les sommes pondérées et le seuil pour chaque combinaison d'entrées comme mentionné ci-dessous.
Si la sortie de la fonction booléenne est 1, alors la somme pondérée sera supérieure ou égale à la valeur de seuil pour ces combinaisons d'entrées.
Si la sortie de la fonction booléenne est 0, alors la somme pondérée sera inférieure à la valeur de seuil pour ces combinaisons d'entrées.
Step 4 - Choisissez les valeurs de poids et de seuil de manière à ce qu'elles satisfassent toutes les relations présentes dans la dernière colonne du tableau ci-dessus.
step 5 - Dessinez le symbol de la porte de seuil avec ces poids et la valeur de seuil.
Exemple
Laissez-nous mettre en œuvre ce qui suit Boolean function en utilisant une seule porte de seuil.
$$Y\left ( X_{1},X_{2},X_{3} \right )=\sum m\left ( 0,2,4,6,7 \right )$$
La fonction booléenne donnée est une fonction à trois variables, qui est représentée sous forme de somme de termes min. leTruth table de cette fonction est illustrée ci-dessous.
| Contributions | Production | ||
|---|---|---|---|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Maintenant, ajoutons (incluons) une colonne supplémentaire au tableau de vérité ci-dessus. Cette dernière colonne contient les relations entreweighted sums (W) and Threshold valeur (T) pour chaque combinaison d'entrées.
| Contributions | Production | Relations entre W & T | ||
|---|---|---|---|---|
| X1 | X2 | X3 | Y | |
| 0 | 0 | 0 | 1 | 0 ≥T |
| 0 | 0 | 1 | 0 | W 3 <T |
| 0 | 1 | 0 | 1 | W 2 ≥ T |
| 0 | 1 | 1 | 0 | W 2 + W 3 <T |
| 1 | 0 | 0 | 1 | W 1 ≥ T |
| 1 | 0 | 1 | 0 | W 1 + W 3 <T |
| 1 | 1 | 0 | 1 | W 1 + W 2 ≥ T |
| 1 | 1 | 1 | 1 | W 1 + W 2 + W 3 ≥ T |
Voici les conclusions du tableau ci-dessus.
La valeur de Threshold doit être nulle ou négative en fonction de la première relation.
La valeur de W 3 doit être négative en fonction des première et seconde relations.
Les valeurs de W 1 et W 2 doivent être supérieures ou égales à la valeur de seuil basée sur les cinquième et troisième relations.
W 2 doit être supérieur à W 3 basé sur la quatrième relation.
Nous pouvons choisir les valeurs suivantes pour les poids et le seuil en fonction des conclusions ci-dessus.
W 1 = 2, W 2 = 1, W 3 = -4 et T = -1
le symbol du seuil de seuil avec les valeurs ci-dessus est indiqué ci-dessous.

Par conséquent, cette porte de seuil implémente le Boolean function, $Y\left ( X_{1}, X_{2},X_{3} \right )=\sum m\left ( 0,2,4,6,7 \right )$.
Nous avons discuté de divers circuits combinatoires dans les chapitres précédents. Tous ces circuits ont un ensemble de sortie (s), qui ne dépend que de la combinaison des entrées présentes. La figure suivante montre leblock diagram du circuit séquentiel.
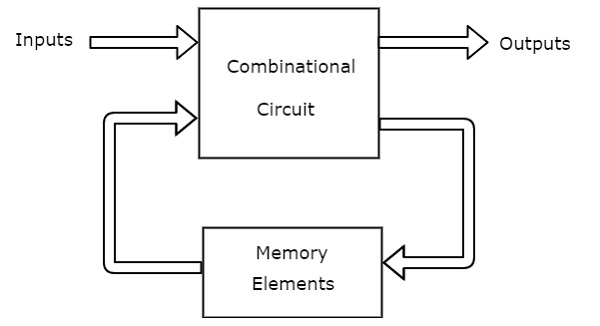
Ce circuit séquentiel contient un ensemble d'entrées et de sortie (s). La (les) sortie (s) du circuit séquentiel dépend non seulement de la combinaison des entrées présentes mais également de la ou des sorties précédentes. La sortie précédente n'est rien d'autre que lepresent state. Par conséquent, les circuits séquentiels contiennent des circuits combinatoires avec des éléments de mémoire (stockage). Certains circuits séquentiels peuvent ne pas contenir de circuits combinatoires, mais uniquement des éléments de mémoire.
Le tableau suivant montre le differences entre circuits combinatoires et circuits séquentiels.
| Circuits combinatoires | Circuits séquentiels |
|---|---|
| Les sorties dépendent uniquement des entrées présentes. | Les sorties dépendent à la fois des entrées présentes et de l'état actuel. |
| Le chemin de rétroaction n'est pas présent. | Un chemin de rétroaction est présent. |
| Les éléments de mémoire ne sont pas nécessaires. | Des éléments de mémoire sont nécessaires. |
| Le signal d'horloge n'est pas nécessaire. | Un signal d'horloge est requis. |
| Conception simple. | Difficile à concevoir. |
Types de circuits séquentiels
Voici les deux types de circuits séquentiels -
- Circuits séquentiels asynchrones
- Circuits séquentiels synchrones
Circuits séquentiels asynchrones
Si certaines ou toutes les sorties d'un circuit séquentiel ne changent pas (affectent) par rapport à la transition active du signal d'horloge, alors ce circuit séquentiel est appelé comme Asynchronous sequential circuit. Cela signifie que toutes les sorties des circuits séquentiels asynchrones ne changent pas (affectent) en même temps. Par conséquent, la plupart des sorties des circuits séquentiels asynchrones sontnot in synchronous avec soit seulement des fronts positifs, soit seulement des fronts négatifs du signal d'horloge.
Circuits séquentiels synchrones
Si toutes les sorties d'un circuit séquentiel changent (affectent) par rapport à la transition active du signal d'horloge, alors ce circuit séquentiel est appelé comme Synchronous sequential circuit. Cela signifie que toutes les sorties des circuits séquentiels synchrones changent (affectent) en même temps. Par conséquent, les sorties de circuits séquentiels synchrones sont synchrones avec soit uniquement des fronts positifs, soit seulement des fronts négatifs du signal d'horloge.
Signal d'horloge et déclenchement
Dans cette section, discutons un par un du signal d'horloge et des types de déclenchement.
Signal d'horloge
Le signal d'horloge est un signal périodique et son heure de marche et son heure d'arrêt ne doivent pas nécessairement être identiques. Nous pouvons représenter le signal d'horloge comme unsquare wave, lorsque l'heure de marche et l'heure d'arrêt sont identiques. Ce signal d'horloge est illustré dans la figure suivante.

Dans la figure ci-dessus, l'onde carrée est considérée comme un signal d'horloge. Ce signal reste au niveau logique haut (5V) pendant un certain temps et reste au niveau logique bas (0V) pendant une durée égale. Ce modèle se répète avec une certaine période de temps. Dans ce cas, letime period sera égal à deux fois le temps ON ou à deux fois le temps OFF.
Nous pouvons représenter le signal d'horloge comme train of pulses, lorsque l'heure de marche et l'heure d'arrêt ne sont pas identiques. Ce signal d'horloge est illustré dans la figure suivante.

Dans la figure ci-dessus, le train d'impulsions est considéré comme un signal d'horloge. Ce signal reste au niveau logique haut (5V) pendant un certain temps et reste au niveau logique bas (0V) pendant un autre temps. Ce modèle se répète avec une certaine période de temps. Dans ce cas, letime period sera égale à la somme du temps ON et du temps OFF.
La réciproque de la période de temps du signal d'horloge est connue sous le nom de frequencydu signal d'horloge. Tous les circuits séquentiels fonctionnent avec un signal d'horloge. Ainsi, la fréquence à laquelle les circuits séquentiels peuvent fonctionner en conséquence la fréquence du signal d'horloge doit être choisie.
Types de déclenchement
Voici les deux types de déclenchement possibles qui sont utilisés dans les circuits séquentiels.
- Déclenchement de niveau
- Déclenchement sur front
Déclenchement de niveau
Il existe deux niveaux, à savoir logique haut et logique bas dans le signal d'horloge. Voici les deuxtypes of level triggering.
- Déclenchement de niveau positif
- Déclenchement de niveau négatif
Si le circuit séquentiel fonctionne avec le signal d'horloge lorsqu'il est en Logic High, alors ce type de déclenchement est appelé Positive level triggering. Il est mis en évidence dans la figure ci-dessous.
Si le circuit séquentiel fonctionne avec le signal d'horloge lorsqu'il est en Logic Low, alors ce type de déclenchement est appelé Negative level triggering. Il est mis en évidence dans la figure suivante.

Déclenchement sur front
Il existe deux types de transitions qui se produisent dans le signal d'horloge. Cela signifie que le signal d'horloge passe de Logic Low à Logic High ou de Logic High à Logic Low.
Voici les deux types of edge triggering basé sur les transitions du signal d'horloge.
- Déclenchement sur front positif
- Déclenchement par front négatif
Si le circuit séquentiel fonctionne avec le signal d'horloge qui passe de Logic Low à Logic High, alors ce type de déclenchement est appelé Positive edge triggering. Il est également appelé déclenchement par front montant. Il est illustré dans la figure suivante.

Si le circuit séquentiel fonctionne avec le signal d'horloge qui passe de Logic High à Logic Low, alors ce type de déclenchement est appelé Negative edge triggering. Il est également appelé déclenchement par front descendant. Il est illustré dans la figure suivante.

Dans les chapitres suivants, nous discuterons de divers circuits séquentiels en fonction du type de déclenchement qui peut y être utilisé.
Il existe deux types d'éléments de mémoire en fonction du type de déclenchement qui convient pour le faire fonctionner.
- Latches
- Flip-flops
Les verrous fonctionnent avec un signal d'activation, qui est level sensitive. Alors que les bascules sont sensibles aux bords. Nous discuterons des bascules dans le prochain chapitre. Parlons maintenant de SR Latch & D Latch un par un.
Loquet SR
SR Latch est également appelé Set Reset Latch. Ce verrou affecte les sorties tant que la validation, E est maintenue à '1'. lecircuit diagram de SR Latch est illustré dans la figure suivante.
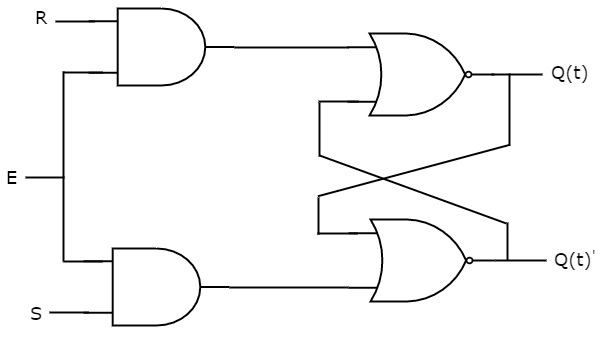
Ce circuit a deux entrées S & R et deux sorties Q (t) & Q (t) '. leupper NOR gate a deux entrées R & complément de l'état présent, Q (t) 'et produit l'état suivant, Q (t + 1) lorsque activé, E est' 1 '.
De même, le lower NOR gate a deux entrées S & état actuel, Q (t) et produit le complément de l'état suivant, Q (t + 1) 'lorsque activé, E est' 1 '.
Nous savons qu'un 2-input NOR gateproduit une sortie, qui est le complément d'une autre entrée lorsque l'une des entrées est «0». De même, il produit une sortie «0», lorsque l'une des entrées est «1».
Si S = 1, alors l'état suivant Q (t + 1) sera égal à «1» quel que soit l'état actuel, les valeurs Q (t).
Si R = 1, alors l'état suivant Q (t + 1) sera égal à «0» quel que soit l'état actuel, les valeurs Q (t).
A tout moment, seule de ces deux entrées doit être «1». Si les deux entrées sont égales à «1», la valeur de l'état suivant Q (t + 1) n'est pas définie.
Le tableau suivant montre les state table du verrou SR.
| S | R | Q (t + 1) |
|---|---|---|
| 0 | 0 | Q (t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | - |
Par conséquent, SR Latch exécute trois types de fonctions telles que Hold, Set & Reset en fonction des conditions d'entrée.
Loquet D
Il y a un inconvénient de SR Latch. C'est la valeur d'état suivante ne peut pas être prédite lorsque les deux entrées S et R sont une. Ainsi, nous pouvons surmonter cette difficulté par D Latch. Il est également appelé Data Latch. lecircuit diagram de D Latch est illustré dans la figure suivante.

Ce circuit a une seule entrée D et deux sorties Q (t) et Q (t) '. D Latch est obtenu à partir de SR Latch en plaçant un inverseur entre les entrées S amp; & R et connectez l'entrée D à S. Cela signifie que nous avons éliminé les combinaisons de S & R sont de même valeur.
Si D = 0 → S = 0 & R = 1, alors l'état suivant Q (t + 1) sera égal à «0» quel que soit l'état actuel, les valeurs de Q (t). Cela correspond à la deuxième ligne de la table d'état SR Latch.
Si D = 1 → S = 1 & R = 0, alors l'état suivant Q (t + 1) sera égal à '1' quel que soit l'état actuel, les valeurs de Q (t). Cela correspond à la troisième ligne de la table d'état SR Latch.
Le tableau suivant montre les state table du loquet D.
| ré | Q (t + 1) |
|---|---|
| 0 | 0 |
| 1 | 1 |
Par conséquent, D Latch Maintient les informations disponibles sur l'entrée de données, D. Cela signifie que la sortie de D Latch est sensible aux changements dans l'entrée, D tant que l'activation est High.
Dans ce chapitre, nous avons implémenté divers verrous en fournissant le couplage croisé entre les portes NOR. De même, vous pouvez implémenter ces verrous à l'aide de portes NAND.
Dans le chapitre précédent, nous avons discuté des verrous. Ce sont les éléments de base des bascules. Nous pouvons implémenter des bascules de deux manières.
Dans la première méthode, cascade two latchesde telle manière que le premier verrou est activé pour chaque impulsion d'horloge positive et le second verrou est activé pour chaque impulsion d'horloge négative. Pour que la combinaison de ces deux loquets devienne une bascule.
Dans la deuxième méthode, nous pouvons implémenter directement la bascule, qui est sensible aux bords. Dans ce chapitre, discutons des points suivantsflip-flops en utilisant la deuxième méthode.
- Flip-Flop SR
- Bascule D
- Bascule JK
- T Flip-Flop
Flip-Flop SR
La bascule SR fonctionne uniquement avec des transitions d'horloge positives ou des transitions d'horloge négatives. Alors que le verrou SR fonctionne avec un signal d'activation. lecircuit diagram de la bascule SR est illustré dans la figure suivante.

Ce circuit a deux entrées S & R et deux sorties Q (t) & Q (t) '. Le fonctionnement de la bascule SR est similaire à SR Latch. Mais cette bascule n'affecte les sorties que lorsqu'une transition positive du signal d'horloge est appliquée au lieu de l'activation active.
Le tableau suivant montre les state table de bascule SR.
| S | R | Q (t + 1) |
|---|---|---|
| 0 | 0 | Q (t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | - |
Ici, Q (t) et Q (t + 1) sont respectivement l'état présent et l'état suivant. Ainsi, la bascule SR peut être utilisée pour l'une de ces trois fonctions telles que Hold, Reset & Set en fonction des conditions d'entrée, lorsqu'une transition positive du signal d'horloge est appliquée. Le tableau suivant montre lescharacteristic table de bascule SR.
| Présenter les entrées | État actuel | État suivant | |
|---|---|---|---|
| S | R | Q(t) | Q(t + 1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | X |
| 1 | 1 | 1 | X |
En utilisant trois variables K-Map, nous pouvons obtenir l'expression simplifiée de l'état suivant, Q (t + 1). lethree variable K-Map pour l'état suivant, Q (t + 1) est montré dans la figure suivante.

Les groupements maximums possibles de ceux adjacents sont déjà indiqués sur la figure. Par conséquent, lasimplified expression pour l'état suivant Q (t + 1) est
$Q\left ( t+1 \right )=S+{R}'Q\left ( t \right )$
Bascule D
La bascule D fonctionne avec uniquement des transitions d'horloge positives ou des transitions d'horloge négatives. Alors que le verrou D fonctionne avec un signal de validation. Cela signifie que la sortie de la bascule D est insensible aux changements de l'entrée, D sauf pour la transition active du signal d'horloge. lecircuit diagram de la bascule D est illustrée dans la figure suivante.

Ce circuit a une seule entrée D et deux sorties Q (t) et Q (t) '. Le fonctionnement de la bascule D est similaire à celui de D Latch. Mais cette bascule n'affecte les sorties que lorsqu'une transition positive du signal d'horloge est appliquée au lieu de l'activation active.
Le tableau suivant montre les state table de la bascule D.
| ré | Qt + 1t + 1 |
|---|---|
| 0 | 0 |
| 1 | 1 |
Par conséquent, la bascule D contient toujours les informations, qui sont disponibles sur l'entrée de données, D de la transition positive antérieure du signal d'horloge. À partir de la table d'état ci-dessus, nous pouvons directement écrire l'équation d'état suivante comme
Q (t + 1) = D
L'état suivant de la bascule D est toujours égal à l'entrée de données, D pour chaque transition positive du signal d'horloge. Par conséquent, les bascules D peuvent être utilisées dans les registres,shift registers et certains des compteurs.
Bascule JK
JK flip-flop est la version modifiée de la bascule SR. Il fonctionne uniquement avec des transitions d'horloge positives ou des transitions d'horloge négatives. lecircuit diagram de la bascule JK est illustrée dans la figure suivante.
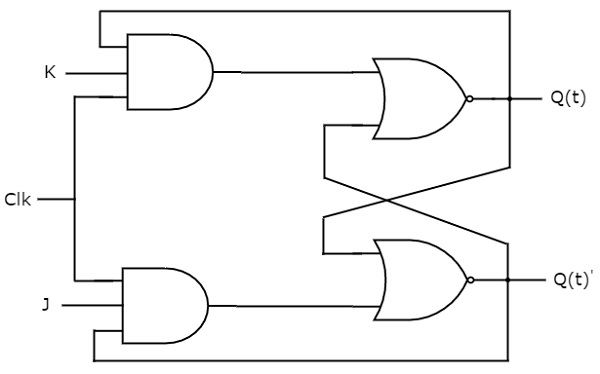
Ce circuit a deux entrées J & K et deux sorties Q (t) & Q (t) '. Le fonctionnement de la bascule JK est similaire à la bascule SR. Ici, nous avons considéré les entrées de la bascule SR commeS = J Q(t)’ et R = KQ(t) afin d'utiliser la bascule SR modifiée pour 4 combinaisons d'entrées.
Le tableau suivant montre les state table de la bascule JK.
| J | K | Q (t + 1) |
|---|---|---|
| 0 | 0 | Q (t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Q (t) ' |
Ici, Q (t) et Q (t + 1) sont respectivement l'état présent et l'état suivant. Ainsi, la bascule JK peut être utilisée pour l'une de ces quatre fonctions telles que Hold, Reset, Set & Complement de l'état actuel en fonction des conditions d'entrée, lorsqu'une transition positive du signal d'horloge est appliquée. Le tableau suivant montre lescharacteristic table de la bascule JK.
| Présenter les entrées | État actuel | État suivant | |
|---|---|---|---|
| J | K | Q(t) | Q(t+1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
En utilisant trois variables K-Map, nous pouvons obtenir l'expression simplifiée de l'état suivant, Q (t + 1). Three variable K-Map pour l'état suivant, Q (t + 1) est montré dans la figure suivante.

Les groupements maximums possibles de ceux adjacents sont déjà indiqués sur la figure. Par conséquent, lasimplified expression pour l'état suivant Q (t + 1) est
$$Q\left ( t+1 \right )=J{Q\left ( t \right )}'+{K}'Q\left ( t \right )$$
T Flip-Flop
T flip-flop est la version simplifiée de JK flip-flop. Il est obtenu en connectant la même entrée «T» aux deux entrées de la bascule JK. Il fonctionne uniquement avec des transitions d'horloge positives ou des transitions d'horloge négatives. lecircuit diagram de la bascule T est illustrée dans la figure suivante.

Ce circuit a une seule entrée T et deux sorties Q (t) et Q (t) '. Le fonctionnement de la bascule T est le même que celui de la bascule JK. Ici, nous avons considéré les entrées de la bascule JK commeJ = T et K = Tafin d'utiliser la bascule JK modifiée pour 2 combinaisons d'entrées. Nous avons donc éliminé les deux autres combinaisons de J & K, pour lesquelles ces deux valeurs sont complémentaires l'une de l'autre dans la bascule T.
Le tableau suivant montre les state table de la bascule T.
| ré | Q (t + 1) |
|---|---|
| 0 | Q (t) |
| 1 | Q (t) ' |
Ici, Q (t) et Q (t + 1) sont respectivement l'état présent et l'état suivant. Ainsi, la bascule T peut être utilisée pour l'une de ces deux fonctions telles que Maintien et Complément de l'état actuel en fonction des conditions d'entrée, lorsqu'une transition positive du signal d'horloge est appliquée. Le tableau suivant montre lescharacteristic table de la bascule T.
| Contributions | État actuel | État suivant |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
À partir du tableau des caractéristiques ci-dessus, nous pouvons directement écrire le next state equation comme
$$Q\left ( t+1 \right )={T}'Q\left ( t \right )+TQ{\left ( t \right )}'$$
$$\Rightarrow Q\left ( t+1 \right )=T\oplus Q\left ( t \right )$$
La sortie de la bascule T bascule toujours pour chaque transition positive du signal d'horloge, lorsque l'entrée T reste à l'état logique haut (1). Par conséquent, la bascule T peut être utilisée danscounters.
Dans ce chapitre, nous avons implémenté diverses bascules en fournissant le couplage croisé entre les portes NOR. De même, vous pouvez implémenter ces bascules à l'aide de portes NAND.
Dans le chapitre précédent, nous avons discuté des quatre bascules, à savoir la bascule SR, la bascule D, la bascule JK et la bascule T. Nous pouvons convertir une bascule en trois bascules restantes en incluant une logique supplémentaire. Donc, il y aura au total douzeflip-flop conversions.
Suivez ces steps pour convertir une bascule en une autre.
Prendre en compte characteristic table de bascule souhaitée.
Remplissez les valeurs d'excitation (entrées) de la bascule donnée pour chaque combinaison de l'état actuel et de l'état suivant. leexcitation table pour toutes les bascules est illustré ci-dessous.
| État actuel | État suivant | Entrées flip-flop SR | Entrée flip-flop D | Entrées flip-flop JK | Entrée flip-flop T | ||
|---|---|---|---|---|---|---|---|
| Q(t) | Q(t+1) | S | R | D | J | K | T |
| 0 | 0 | 0 | X | 0 | 0 | X | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | X | 1 |
| 1 | 0 | 0 | 1 | 0 | X | 1 | 1 |
| 1 | 1 | X | 0 | 1 | X | 0 | 0 |
Obtenir le simplified expressionspour chaque entrée d'excitation. Si nécessaire, utilisez Kmaps pour simplifier.
Dessine le circuit diagram de bascule désirée selon les expressions simplifiées en utilisant une bascule donnée et des portes logiques nécessaires.
Maintenant, convertissons quelques bascules en d'autres. Suivez le même processus pour les conversions de bascule restantes.
Flip-Flop SR vers d'autres conversions Flip-Flop
Voici les trois conversions possibles de bascule SR en d'autres bascules.
- Flip-flop SR à bascule D
- Flip-flop SR à bascule JK
- Flip-flop SR à bascule T
Conversion de bascule SR en bascule D
Ici, la bascule donnée est la bascule SR et la bascule souhaitée est la bascule D. Par conséquent, considérez ce qui suitcharacteristic table de la bascule D.
| Entrée flip-flop D | État actuel | État suivant |
|---|---|---|
| D | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Nous savons que la bascule SR a deux entrées S & R. Alors, notez les valeurs d'excitation de la bascule SR pour chaque combinaison de valeurs d'état actuel et d'état suivant. Le tableau suivant montre le tableau des caractéristiques de la bascule D avec leexcitation inputs de bascule SR.
| Entrée flip-flop D | État actuel | État suivant | Entrées flip-flop SR | |
|---|---|---|---|---|
| D | Q(t) | Q(t + 1) | S | R |
| 0 | 0 | 0 | 0 | X |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | X | 0 |
À partir du tableau ci-dessus, nous pouvons écrire le Boolean functions pour chaque entrée comme ci-dessous.
$$S=m_{2}+d_{3}$$
$$R=m_{1}+d_{0}$$
Nous pouvons utiliser 2 K-Maps variables pour obtenir des expressions simplifiées pour ces entrées. lek-Maps pour S & R sont indiqués ci-dessous.

Donc, nous avons obtenu S = D & R = D 'après avoir simplifié. lecircuit diagram de la bascule D est illustrée dans la figure suivante.

Ce circuit se compose d'une bascule SR et d'un inverseur. Cet onduleur produit une sortie, qui est le complément de l'entrée, D. Ainsi, le circuit global a une seule entrée, D et deux sorties Q (t) et Q (t) '. Par conséquent, c'est unD flip-flop. De même, vous pouvez effectuer deux autres conversions.
D Flip-Flop vers d'autres conversions Flip-Flop
Voici les trois conversions possibles de la bascule D en d'autres bascules.
- Flip-flop D à T bascule
- Flip-flop D à bascule SR
- Bascule D à bascule JK
Conversion de bascule D en bascule T
Ici, la bascule donnée est la bascule D et la bascule souhaitée est la bascule T. Par conséquent, considérez ce qui suitcharacteristic table de la bascule T.
| Entrée flip-flop T | État actuel | État suivant |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Nous savons que la bascule D a une seule entrée D. Donc, notez les valeurs d'excitation de la bascule D pour chaque combinaison de valeurs d'état actuel et d'état suivant. Le tableau suivant montre le tableau des caractéristiques de la bascule T avec leexcitation input de la bascule D.
| Entrée flip-flop T | État actuel | État suivant | Entrée flip-flop D |
|---|---|---|---|
| T | Q(t) | Q(t + 1) | D |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
À partir du tableau ci-dessus, nous pouvons directement écrire le Boolean function de D comme ci-dessous.
$$D=T\oplus Q\left ( t \right )$$
Donc, nous avons besoin d'une porte OU exclusif à deux entrées avec une bascule D. lecircuit diagram de la bascule T est illustrée dans la figure suivante.

Ce circuit se compose d'une bascule D et d'une porte OU exclusif. Cette porte OU exclusif produit une sortie, qui est Ex-OU de T et Q (t). Ainsi, le circuit global a une seule entrée, T et deux sorties Q (t) et Q (t) '. Par conséquent, c'est unT flip-flop. De même, vous pouvez effectuer deux autres conversions.
JK Flip-Flop vers d'autres conversions Flip-Flop
Voici les trois conversions possibles de bascule JK en d'autres bascules.
- Bascule JK à bascule T
- Bascule JK à bascule D
- Bascule JK à bascule SR
Conversion de bascule JK en bascule T
Ici, la bascule donnée est la bascule JK et la bascule souhaitée est la bascule T. Par conséquent, considérez ce qui suitcharacteristic table de la bascule T.
| Entrée flip-flop T | État actuel | État suivant |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Nous savons que la bascule JK a deux entrées J & K. Alors, notez les valeurs d'excitation de la bascule JK pour chaque combinaison de valeurs d'état actuel et d'état suivant. Le tableau suivant montre le tableau des caractéristiques de la bascule T avec leexcitation inputs de la bascule JK.
| Entrée flip-flop T | État actuel | État suivant | Entrées flip-flop JK | |
|---|---|---|---|---|
| T | Q(t) | Q(t + 1) | J | K |
| 0 | 0 | 0 | 0 | X |
| 0 | 1 | 1 | X | 0 |
| 1 | 0 | 1 | 1 | X |
| 1 | 1 | 0 | X | 1 |
À partir du tableau ci-dessus, nous pouvons écrire le Boolean functions pour chaque entrée comme ci-dessous.
$$J=m_{2}+d_{1}+d_{3}$$
$$K=m_{3}+d_{0}+d_{2}$$
Nous pouvons utiliser 2 K-Maps variables pour obtenir des expressions simplifiées pour ces deux entrées. lek-Maps pour J & K sont indiqués ci-dessous.

Donc, nous avons obtenu, J = T & K = T après simplification. lecircuit diagram de la bascule T est illustrée dans la figure suivante.

Ce circuit se compose uniquement d'une bascule JK. Il ne nécessite aucune autre porte. Connectez simplement la même entrée T aux deux J et K. Ainsi, le circuit global a une seule entrée, T et deux sorties Q (t) et Q (t) '. Par conséquent, c'est unT flip-flop. De même, vous pouvez effectuer deux autres conversions.
T Flip-Flop vers d'autres conversions Flip-Flop
Voici les trois conversions possibles de la bascule T en d'autres bascules.
- Bascule T à bascule D
- T bascule vers bascule SR
- T bascule vers bascule JK
Conversion de bascule T en bascule D
Ici, la bascule donnée est la bascule T et la bascule souhaitée est la bascule D. Par conséquent, considérez le tableau des caractéristiques de la bascule D et notez les valeurs d'excitation de la bascule T pour chaque combinaison de valeurs d'état actuel et d'état suivant. Le tableau suivant montre lescharacteristic table de la bascule D avec le excitation input de la bascule T.
| Entrée flip-flop D | État actuel | État suivant | Entrée flip-flop T | |
|---|---|---|---|---|
| D | Q(t) | Q(t + 1) | T | |
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | |
À partir du tableau ci-dessus, nous pouvons directement écrire la fonction booléenne de T comme ci-dessous.
$$T=D\oplus Q\left ( t \right )$$
Donc, nous avons besoin d'une porte OU exclusif à deux entrées avec une bascule T. lecircuit diagram de la bascule D est illustrée dans la figure suivante.

Ce circuit se compose d'une bascule T et d'une porte OU exclusif. Cette porte OU exclusif produit une sortie, qui est Ex-OU de D et Q (t). Ainsi, le circuit global a une seule entrée, D et deux sorties Q (t) et Q (t) '. Par conséquent, c'est unD flip-flop. De même, vous pouvez effectuer deux autres conversions.
Nous savons qu'une bascule peut stocker un bit d'information. Afin de stocker plusieurs bits d'informations, nous avons besoin de plusieurs bascules. Le groupe de bascules, qui sont utilisées pour contenir (stocker) les données binaires, est appeléregister.
Si le registre est capable de décaler des bits vers la droite ou vers la gauche, on parle de shift register. Un registre à décalage «N» bits contient «N» bascules. Voici les quatre types de registres à décalage basés sur l'application d'entrées et l'accès aux sorties.
- Registre à décalage Serial In - Serial Out
- Registre à décalage Serial In - Parallel Out
- Registre à décalage Parallel In - Serial Out
- Registre à décalage Parallel In - Parallel Out
Registre de décalage d'entrée série - sortie série (SISO)
Le registre à décalage, qui permet une entrée série et produit une sortie série, est appelé Serial In - Serial Out (SISO)registre à décalage. leblock diagram du registre à décalage SISO 3 bits est illustré dans la figure suivante.

Ce schéma de principe se compose de trois bascules D, qui sont cascaded. Cela signifie que la sortie d'une bascule D est connectée en tant qu'entrée de la bascule D suivante. Toutes ces bascules sont synchrones entre elles puisque, le même signal d'horloge est appliqué à chacune.
Dans ce registre à décalage, nous pouvons envoyer les bits en série à partir de l'entrée de la bascule D la plus à gauche. Par conséquent, cette entrée est également appeléeserial input. Pour chaque déclenchement de front montant du signal d'horloge, les données passent d'un étage à l'autre. Ainsi, nous pouvons recevoir les bits en série à partir de la sortie de la bascule D la plus à droite. Par conséquent, cette sortie est également appeléeserial output.
Exemple
Voyons le fonctionnement du registre à décalage SISO 3 bits en envoyant les informations binaires “011” de LSB à MSB en série à l'entrée.
Supposons que l'état initial des bascules D de l'extrême gauche à l'extrême droite est $Q_{2}Q_{1}Q_{0}=000$. Nous pouvons comprendre leworking of 3-bit SISO shift register du tableau suivant.
| No de front positif de l'horloge | Entrée série | Q 2 | Q 1 | Q 0 |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1 (LSB) | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 0 (MSB) | 0 | 1 | 1 (LSB) |
| 4 | - | - | 0 | 1 |
| 5 | - | - | - | 0 (MSB) |
L'état initial des bascules D en l'absence de signal d'horloge est $Q_{2}Q_{1}Q_{0}=000$. Ici, la sortie série provient de$Q_{0}$. Ainsi, le LSB (1) est reçu au 3 ème front positif de l'horloge et le MSB (0) est reçu au 5 ème front positif de l'horloge.
Par conséquent, le registre à décalage SISO à 3 bits nécessite cinq impulsions d'horloge afin de produire la sortie valide. De même, leN-bit SISO shift register a besoin 2N-1 des impulsions d'horloge afin de décaler les informations de «N» bits.
Registre à décalage d'entrée série - sortie parallèle (SIPO)
Le registre à décalage, qui permet une entrée série et produit une sortie parallèle, est appelé Serial In - Parallel Out (SIPO) shift register. The block diagram of 3-bit SIPO shift register is shown in the following figure.
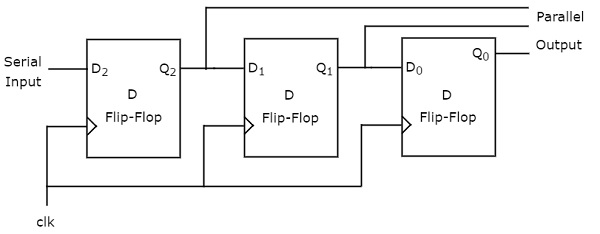
This circuit consists of three D flip-flops, which are cascaded. That means, output of one D flip-flop is connected as the input of next D flip-flop. All these flip-flops are synchronous with each other since, the same clock signal is applied to each one.
In this shift register, we can send the bits serially from the input of left most D flip-flop. Hence, this input is also called as serial input. For every positive edge triggering of clock signal, the data shifts from one stage to the next. In this case, we can access the outputs of each D flip-flop in parallel. So, we will get parallel outputs from this shift register.
Example
Let us see the working of 3-bit SIPO shift register by sending the binary information “011” from LSB to MSB serially at the input.
Assume, initial status of the D flip-flops from leftmost to rightmost is $Q_{2}Q_{1}Q_{0}=000$. Here, $Q_{2}$ & $Q_{0}$ are MSB & LSB respectively. We can understand the working of 3-bit SIPO shift register from the following table.
| No of positive edge of Clock | Serial Input | Q2(MSB) | Q1 | Q0(LSB) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1(LSB) | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 0(MSB) | 0 | 1 | 1 |
The initial status of the D flip-flops in the absence of clock signal is $Q_{2}Q_{1}Q_{0}=000$. The binary information “011” is obtained in parallel at the outputs of D flip-flops for third positive edge of clock.
So, the 3-bit SIPO shift register requires three clock pulses in order to produce the valid output. Similarly, the N-bit SIPO shift register requires N clock pulses in order to shift ‘N’ bit information.
Parallel In − Serial Out (PISO) Shift Register
The shift register, which allows parallel input and produces serial output is known as Parallel In − Serial Out (PISO) shift register. The block diagram of 3-bit PISO shift register is shown in the following figure.

This circuit consists of three D flip-flops, which are cascaded. That means, output of one D flip-flop is connected as the input of next D flip-flop. All these flip-flops are synchronous with each other since, the same clock signal is applied to each one.
In this shift register, we can apply the parallel inputs to each D flip-flop by making Preset Enable to 1. For every positive edge triggering of clock signal, the data shifts from one stage to the next. So, we will get the serial output from the right most D flip-flop.
Example
Let us see the working of 3-bit PISO shift register by applying the binary information “011” in parallel through preset inputs.
Since the preset inputs are applied before positive edge of Clock, the initial status of the D flip-flops from leftmost to rightmost will be $Q_{2}Q_{1}Q_{0}=011$. We can understand the working of 3-bit PISO shift register from the following table.
| No of positive edge of Clock | Q2 | Q1 | Q0 |
|---|---|---|---|
| 0 | 0 | 1 | 1(LSB) |
| 1 | - | 0 | 1 |
| 2 | - | - | 0(LSB) |
Here, the serial output is coming from $Q_{0}$. So, the LSB (1) is received before applying positive edge of clock and the MSB (0) is received at 2nd positive edge of clock.
Therefore, the 3-bit PISO shift register requires two clock pulses in order to produce the valid output. Similarly, the N-bit PISO shift register requires N-1 clock pulses in order to shift ‘N’ bit information.
Parallel In - Parallel Out (PIPO) Shift Register
The shift register, which allows parallel input and produces parallel output is known as Parallel In − Parallel Out (PIPO) shift register. The block diagram of 3-bit PIPO shift register is shown in the following figure.

This circuit consists of three D flip-flops, which are cascaded. That means, output of one D flip-flop is connected as the input of next D flip-flop. All these flip-flops are synchronous with each other since, the same clock signal is applied to each one.
In this shift register, we can apply the parallel inputs to each D flip-flop by making Preset Enable to 1. We can apply the parallel inputs through preset or clear. These two are asynchronous inputs. That means, the flip-flops produce the corresponding outputs, based on the values of asynchronous inputs. In this case, the effect of outputs is independent of clock transition. So, we will get the parallel outputs from each D flip-flop.
Exemple
Voyons le fonctionnement du registre à décalage PIPO 3 bits en appliquant les informations binaires “011” en parallèle via des entrées préréglées.
Puisque les entrées préréglées sont appliquées avant le front positif de l'horloge, l'état initial des bascules D de l'extrême gauche à l'extrême droite sera $Q_{2}Q_{1}Q_{0}=011$. Donc, les informations binaires“011” est obtenu en parallèle aux sorties des bascules D avant d'appliquer un front positif d'horloge.
Par conséquent, le registre à décalage PIPO à 3 bits nécessite des impulsions d'horloge nulles afin de produire la sortie valide. De même, leN-bit PIPO shift register ne nécessite aucune impulsion d'horloge pour décaler les informations de «N» bits.
Dans le chapitre précédent, nous avons discuté de quatre types de registres à décalage. En fonction de l'exigence, nous pouvons utiliser l'un de ces registres à décalage. Voici les applications des registres à décalage.
Le registre à décalage est utilisé comme Parallel to serial converter, qui convertit les données parallèles en données série. Il est utilisé au niveau de la section émetteur après le bloc convertisseur analogique-numérique (ADC).
Le registre à décalage est utilisé comme Serial to parallel converter, qui convertit les données série en données parallèles. Il est utilisé au niveau de la section du récepteur avant le bloc convertisseur numérique-analogique (DAC).
Le registre à décalage ainsi que quelques portes supplémentaires génèrent la séquence de zéros et de uns. Par conséquent, il est utilisé commesequence generator.
Les registres à décalage sont également utilisés comme counters. Il existe deux types de compteurs en fonction du type de sortie de la bascule D la plus à droite connectée à l'entrée série. Ce sont le compteur Ring et le compteur Johnson Ring.
Dans ce chapitre, discutons de ces deux compteurs un par un.
Compteur de sonneries
Dans le chapitre précédent, nous avons discuté du fonctionnement de Serial In - Parallel Out (SIPO)registre à décalage. Il accepte les données de l'extérieur sous forme série et il a besoin de «N» impulsions d'horloge pour décaler les données de «N» bits.
De même, ‘N’ bit Ring countereffectue l'opération similaire. Mais, la seule différence est que la sortie de la bascule D la plus à droite est donnée comme entrée de la bascule D la plus à gauche au lieu d'appliquer des données de l'extérieur. Par conséquent, Ring counter produit une séquence d'états (motif de zéros et de uns) et il se répète pour chaque‘N’ clock cycles.
le block diagram du compteur en anneau à 3 bits est illustré dans la figure suivante.
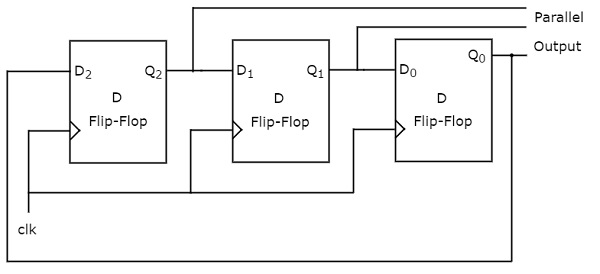
Le compteur en anneau à 3 bits contient uniquement un registre à décalage SIPO à 3 bits. La sortie de la bascule D la plus à droite est connectée à l'entrée série de la bascule D la plus à gauche.
Supposons que l'état initial des bascules D de l'extrême gauche à l'extrême droite est $Q_{2}Q_{1}Q_{0}=001$. Ici,$Q_{2}$ & $Q_{0}$sont respectivement MSB et LSB. Nous pouvons comprendre leworking of Ring counter du tableau suivant.
| No de front positif de l'horloge | Entrée série = Q 0 | Q 2 (MSB) | Q 1 | Q 0 (LSB) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 |
L'état initial des bascules D en l'absence de signal d'horloge est $Q_{2}Q_{1}Q_{0}=001$. Cet état se répète toutes les trois transitions de front montant du signal d'horloge.
Par conséquent, ce qui suit operations ont lieu pour chaque front positif du signal d'horloge.
L'entrée série de la première bascule D obtient la sortie précédente de la troisième bascule. Ainsi, la sortie actuelle de la première bascule D est égale à la sortie précédente de la troisième bascule.
Les sorties précédentes des première et deuxième bascules D sont décalées vers la droite d'un bit. Cela signifie que les sorties présentes des deuxième et troisième bascules D sont égales aux sorties précédentes des première et deuxième bascules D.
Compteur de bagues Johnson
Le fonctionnement de Johnson Ring counterest similaire à celui du compteur Ring. Mais, la seule différence est que la sortie complémentée de la bascule D la plus à droite est donnée comme entrée de la bascule D la plus à gauche au lieu de la sortie normale. Par conséquent, le compteur Johnson Ring 'N' bit produit une séquence d'états (motif de zéros et de uns) et il se répète pour chaque‘2N’ clock cycles.
Le compteur Johnson Ring est également appelé Twisted Ring counteret changer le compteur de l'anneau de queue. leblock diagram du compteur Johnson Ring 3 bits est illustré dans la figure suivante.

Le compteur Johnson Ring à 3 bits contient également uniquement un registre à décalage SIPO à 3 bits. La sortie complétée de la bascule D la plus à droite est connectée à l'entrée série de la bascule D la plus à gauche.
Supposons qu'au départ, toutes les bascules D soient effacées. Alors,$Q_{2}Q_{1}Q_{0}=000$. Ici,$Q_{2}$ & $Q_{0}$sont respectivement MSB et LSB. Nous pouvons comprendre leworking du compteur Johnson Ring du tableau suivant.
| No de front positif de l'horloge | Entrée série = Q 0 | Q 2 (MSB) | Q 1 | Q 0 (LSB) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 1 | 1 | 1 | 1 |
| 4 | 0 | 0 | 1 | 1 |
| 5 | 0 | 0 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 |
L'état initial des bascules D en l'absence de signal d'horloge est $Q_{2}Q_{1}Q_{0}=000$. Cet état se répète toutes les six transitions de front montant du signal d'horloge.
Par conséquent, ce qui suit operations ont lieu pour chaque front positif du signal d'horloge.
L'entrée série de la première bascule D obtient la sortie précédente complémentée de la troisième bascule. Ainsi, la sortie actuelle de la première bascule D est égale à la sortie complémentée précédente de la troisième bascule.
Les sorties précédentes des première et deuxième bascules D sont décalées vers la droite d'un bit. Cela signifie que les sorties présentes des deuxième et troisième bascules D sont égales aux sorties précédentes des première et deuxième bascules D.
Dans les deux chapitres précédents, nous avons discuté de divers registres à décalage et counters using D flipflops. Maintenant, laissez-nous discuter de divers compteurs utilisant des bascules T. Nous savons que la bascule T bascule la sortie soit pour chaque front positif du signal d'horloge soit pour le front négatif du signal d'horloge.
Un compteur binaire «N» bits se compose de bascules «N» T. Si le compteur compte de 0 à 2 - 1, alors il est appelé comme binaire up counter. De même, si le compteur décompte à partir de 2 - 1 à 0, alors il est appelé comme binaire down counter.
Il y en a deux types of counters basé sur les bascules qui sont connectées en synchrone ou non.
- Compteurs asynchrones
- Compteurs synchrones
Compteurs asynchrones
Si les bascules ne reçoivent pas le même signal d'horloge, alors ce compteur est appelé comme Asynchronous counter. La sortie de l'horloge système est appliquée comme signal d'horloge uniquement à la première bascule. Les bascules restantes reçoivent le signal d'horloge de la sortie de sa bascule d'étage précédent. Par conséquent, les sorties de toutes les bascules ne changent pas (affectent) en même temps.
Maintenant, laissez-nous discuter des deux compteurs suivants un par un.
- Compteur ascendant binaire asynchrone
- Décompteur binaire asynchrone
Compteur ascendant binaire asynchrone
Un compteur ascendant binaire asynchrone «N» bit se compose de «N» T bascules. Il compte de 0 à 2 - 1. Le block diagram du compteur ascendant binaire asynchrone 3 bits est illustré dans la figure suivante.

Le compteur ascendant binaire asynchrone à 3 bits contient trois bascules T et l'entrée T de toutes les bascules est connectée à «1». Toutes ces bascules sont déclenchées par un front négatif mais les sorties changent de manière asynchrone. Le signal d'horloge est directement appliqué à la première bascule T. Donc, la sortie de la première bascule Ttoggles pour chaque front négatif du signal d'horloge.
La sortie de la première bascule T est appliquée comme signal d'horloge pour la deuxième bascule T. Ainsi, la sortie de la deuxième bascule T bascule pour chaque front négatif de la sortie de la première bascule T. De même, la sortie de la troisième bascule T bascule pour chaque front négatif de sortie de la deuxième bascule T, puisque la sortie de la deuxième bascule T agit comme le signal d'horloge pour la troisième bascule T.
Supposons que l'état initial des bascules T de l'extrême droite à l'extrême gauche est $Q_{2}Q_{1}Q_{0}=000$. Ici,$Q_{2}$ & $Q_{0}$sont respectivement MSB et LSB. Nous pouvons comprendre leworking du compteur binaire asynchrone 3 bits du tableau suivant.
| Pas de front négatif de l'horloge | Q 0 (LSB) | Q 1 | Q 2 (MSB) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 1 | 1 | 0 |
| 4 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 |
| sept | 1 | 1 | 1 |
Ici $Q_{0}$ basculé pour chaque front négatif du signal d'horloge. $Q_{1}$ basculé pour chaque $Q_{0}$qui va de 1 à 0, sinon resté dans l'état précédent. De même,$Q_{2}$ basculé pour chaque $Q_{1}$ qui va de 1 à 0, sinon resté dans l'état précédent.
L'état initial des bascules T en l'absence de signal d'horloge est $Q_{2}Q_{1}Q_{0}=000$. Celui-ci est incrémenté de un pour chaque front négatif du signal d'horloge et atteint sa valeur maximale au 7ème front négatif du signal d'horloge. Ce motif se répète lorsque d'autres fronts négatifs du signal d'horloge sont appliqués.
Compteur décroissant binaire asynchrone
Un décompteur binaire asynchrone à «N» bits se compose de «N» T bascules. Ça compte à partir de 2 - 1 à 0. Le block diagram du compteur décroissant binaire asynchrone 3 bits est illustré dans la figure suivante.

Le schéma de principe du compteur décroissant binaire asynchrone 3 bits est similaire au schéma fonctionnel du compteur décroissant binaire asynchrone 3 bits. Mais, la seule différence est qu'au lieu de connecter les sorties normales d'une bascule à un étage comme signal d'horloge pour la bascule d'étage suivante, connectez lecomplemented outputsd'une bascule d'étage comme signal d'horloge pour la bascule d'étage suivante. La sortie complétée va de 1 à 0 est la même que la sortie normale passe de 0 à 1.
Supposons que l'état initial des bascules T de l'extrême droite à l'extrême gauche est $Q_{2}Q_{1}Q_{0}=000$. Ici,$Q_{2}$ & $Q_{0}$sont respectivement MSB et LSB. Nous pouvons comprendre leworking du compteur décroissant binaire asynchrone 3 bits du tableau suivant.
| Pas de front négatif de l'horloge | Q 0 (LSB) | Q 1 | Q 2 (MSB) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 |
| 4 | 0 | 0 | 1 |
| 5 | 1 | 1 | 0 |
| 6 | 0 | 1 | 0 |
| sept | 1 | 0 | 0 |
Ici $Q_{0}$ basculé pour chaque front négatif du signal d'horloge. $Q_{1}$ basculé pour chaque $Q_{0}$qui va de 0 à 1, sinon resté dans l'état précédent. De même,$Q_{2}$ basculé pour chaque $Q_{1}$ qui va de 0 à 1, sinon resté dans l'état précédent.
L'état initial des bascules T en l'absence de signal d'horloge est $Q_{2}Q_{1}Q_{0}=000$. Ceci est décrémenté d'un pour chaque bord négatif du signal d'horloge et atteint la même valeur à 8 ème front négatif du signal d'horloge. Ce motif se répète lorsque d'autres fronts négatifs du signal d'horloge sont appliqués.
Compteurs synchrones
Si toutes les bascules reçoivent le même signal d'horloge, alors ce compteur est appelé comme Synchronous counter. Par conséquent, les sorties de toutes les bascules changent (affectent) en même temps.
Maintenant, laissez-nous discuter des deux compteurs suivants un par un.
- Compteur ascendant binaire synchrone
- Décompteur binaire synchrone
Compteur ascendant binaire synchrone
Un compteur binaire ascendant synchrone «N» bit se compose de bascules «N» T. Il compte de 0 à 2 - 1. Le block diagram du compteur ascendant binaire synchrone 3 bits est illustré dans la figure suivante.

Le compteur binaire haut synchrone à 3 bits contient trois bascules T et une porte ET à 2 entrées. Toutes ces bascules sont déclenchées par un front négatif et les sorties des bascules changent (affectent) de manière synchrone. Les entrées T des première, deuxième et troisième bascules sont 1,$Q_{0}$ & $Q_{1}Q_{0}$ respectivement.
La sortie de la première bascule T togglespour chaque front négatif du signal d'horloge. La sortie de la seconde bascule T bascule pour chaque front négatif du signal d'horloge si$Q_{0}$ est 1. La sortie de la troisième bascule T bascule pour chaque front négatif du signal d'horloge si les deux $Q_{0}$ & $Q_{1}$ sont 1.
Décompteur binaire synchrone
Un décompteur binaire synchrone à «N» bits se compose de bascules «N» T. Ça compte à partir de 2 - 1 à 0. Le block diagram du compteur décroissant binaire synchrone 3 bits est illustré dans la figure suivante.

Le décompteur binaire synchrone à 3 bits contient trois bascules T et une porte ET à 2 entrées. Toutes ces bascules sont déclenchées par un front négatif et les sorties des bascules changent (affectent) de manière synchrone. Les entrées T des première, deuxième et troisième bascules sont 1,${Q_{0}}'$ & ' ${Q_{1}}'$${Q_ {0}} '$ respectivement.
La sortie de la première bascule T togglespour chaque front négatif du signal d'horloge. La sortie de la seconde bascule T bascule pour chaque front négatif du signal d'horloge si $ {Q_ {0}} '$ is 1. The output of third T flip-flop toggles for every negative edge of clock signal if both ${Q_ {1}} '$ & ${Q_ {0}} '$ valent 1.
Nous savons que les circuits séquentiels synchrones changent (affectent) leurs états pour chaque transition positive (ou négative) du signal d'horloge en fonction de l'entrée. Ainsi, ce comportement des circuits séquentiels synchrones peut être représenté sous forme graphique et il est connu commestate diagram.
Un circuit séquentiel synchrone est également appelé Finite State Machine(FSM), s'il a un nombre fini d'états. Il existe deux types de FSM.
- Machine d'état farineuse
- Machine d'état de Moore
Maintenant, parlons de ces deux machines à états une par une.
Machine d'état farineuse
Une machine à états finis est dite machine à états de Mealy, si les sorties dépendent à la fois des entrées et des états présents. leblock diagram de la machine d'état Mealy est illustré dans la figure suivante.
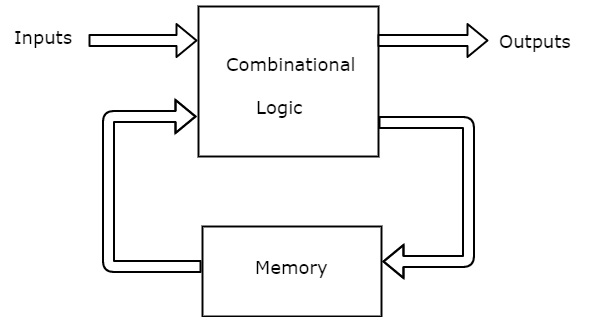
Comme le montre la figure, il y a deux parties présentes dans la machine à états Mealy. Ce sont la logique combinatoire et la mémoire. La mémoire est utile pour fournir une partie ou une partie des sorties précédentes(present states) comme entrées de la logique combinatoire.
Ainsi, sur la base des entrées et des états présents, la machine à états Mealy produit des sorties. Par conséquent, les sorties ne seront valides qu'à la transition positive (ou négative) du signal d'horloge.
le state diagram de la machine d'état Mealy est illustré dans la figure suivante.
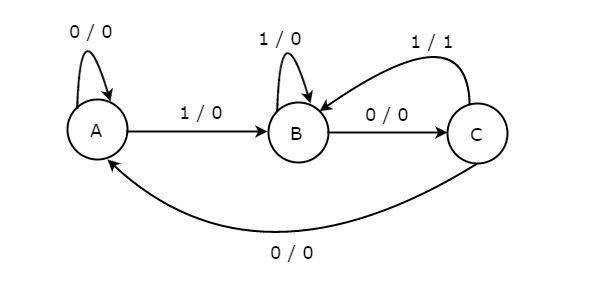
Dans la figure ci-dessus, il y a trois états, à savoir A, B et C. Ces états sont étiquetés à l'intérieur des cercles et chaque cercle correspond à un état. Les transitions entre ces états sont représentées par des lignes dirigées. Ici, 0/0, 1/0 & 1/1 indiqueinput / output. Dans la figure ci-dessus, il y a deux transitions de chaque état en fonction de la valeur de l'entrée, x.
En général, le nombre d'états requis dans la machine à états Mealy est inférieur ou égal au nombre d'états requis dans la machine à états de Moore. Il existe une machine à états de Moore équivalente pour chaque machine à états de Mealy.
Machine d'état de Moore
Une machine à états finis est dite machine à états de Moore, si les sorties ne dépendent que des états présents. leblock diagram de la machine à états de Moore est illustrée dans la figure suivante.

Comme le montre la figure, il y a deux parties présentes dans la machine à états de Moore. Ce sont la logique combinatoire et la mémoire. Dans ce cas, les entrées actuelles et les états actuels déterminent les états suivants. Ainsi, sur la base des états suivants, la machine à états de Moore produit les sorties. Par conséquent, les sorties ne seront valides qu'après la transition de l'état.
le state diagram de la machine à états de Moore est illustrée dans la figure suivante.

Dans la figure ci-dessus, il y a quatre états, à savoir A, B, C et D. Ces états et les sorties respectives sont étiquetés à l'intérieur des cercles. Ici, seule la valeur d'entrée est étiquetée sur chaque transition. Dans la figure ci-dessus, il y a deux transitions de chaque état en fonction de la valeur de l'entrée, x.
En général, le nombre d'états requis dans la machine à états de Moore est supérieur ou égal au nombre d'états requis dans la machine à états Mealy. Il existe une machine à états Mealy équivalente pour chaque machine à états de Moore. Donc, en fonction de l'exigence, nous pouvons utiliser l'un d'entre eux.
Chaque digital systempeut être divisé en deux parties. Ce sont des circuits de chemin de données (numériques) et des circuits de commande. Les circuits de chemin de données exécutent les fonctions telles que le stockage d'informations binaires (données) et le transfert de données d'un système à l'autre système. Alors que les circuits de contrôle déterminent le flux des opérations des circuits numériques.
Il est difficile de décrire le comportement des grandes machines à états à l'aide de diagrammes d'états. Pour surmonter cette difficulté, des graphiques ASM (Algorithmic State Machine) peuvent être utilisés.ASM chartssont similaires aux organigrammes. Ils sont utilisés pour représenter le flux des tâches à effectuer par les circuits de chemin de données et les circuits de commande.
Composants de base des graphiques ASM
Voici les trois composants de base des graphiques ASM.
- Zone d'état
- Boîte de décision
- Boîte de sortie conditionnelle
Zone d'état
La zone d'état est représentée sous forme rectangulaire. Chaque case d'état représente un état du circuit séquentiel. lesymbol La zone d'état est illustrée dans la figure suivante.
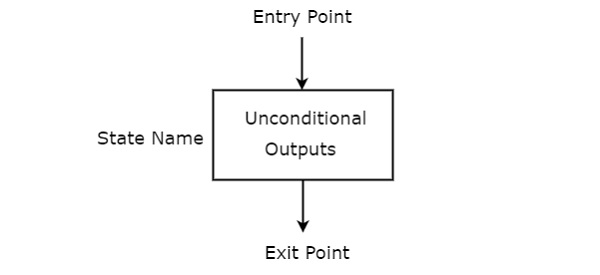
Il a un point d'entrée et un point de sortie. Le nom de l'état est placé à gauche de la zone d'état. Les sorties inconditionnelles correspondant à cet état peuvent être placées à l'intérieur de la boîte d'état.Moore les sorties de la machine d'état peuvent également être placées à l'intérieur de la boîte d'état.
Boîte de décision
La boîte de décision est représentée en forme de losange. lesymbol de la boîte de décision est illustré dans la figure suivante.

Il a un point d'entrée et deux chemins de sortie. Les entrées ou expressions booléennes peuvent être placées à l'intérieur de la boîte de décision, qui doit être vérifiée si elles sont vraies ou fausses. Si la condition est vraie, alors il préférera path1. Sinon, il préférera path2.
Boîte de sortie conditionnelle
La boîte de sortie conditionnelle est représentée sous forme ovale. lesymbol de la boîte de sortie conditionnelle est illustré dans la figure suivante.

Il a également un point d'entrée et un point de sortie similaires à la boîte d'état. Les sorties conditionnelles peuvent être placées à l'intérieur de la boîte d'état. En général,Mealyles sorties de la machine d'état sont représentées dans la boîte de sortie conditionnelle. Ainsi, en fonction de l'exigence, nous pouvons utiliser correctement les composants ci-dessus pour dessiner des graphiques ASM.