Mathématiques discrètes - Ensembles

Mathématicien allemand G. Cantorintroduit le concept d'ensembles. Il avait défini un ensemble comme une collection d'objets définis et distinguables sélectionnés au moyen de certaines règles ou descriptions.

Setla théorie constitue la base de plusieurs autres domaines d'étude comme la théorie du comptage, les relations, la théorie des graphes et les machines à états finis. Dans ce chapitre, nous couvrirons les différents aspects deSet Theory.

Ensemble - Définition

Un ensemble est une collection non ordonnée de différents éléments. Un ensemble peut être écrit explicitement en listant ses éléments à l'aide de set bracket. Si l'ordre des éléments est modifié ou si tout élément d'un ensemble est répété, il n'apporte aucune modification à l'ensemble.

Quelques exemples d'ensembles

Un ensemble de tous les entiers positifs
Un ensemble de toutes les planètes du système solaire
Un ensemble de tous les États de l'Inde
Un ensemble de toutes les lettres minuscules de l'alphabet

Représentation d'un ensemble

Les ensembles peuvent être représentés de deux manières -

Liste ou forme tabulaire
Définir la notation du générateur

Liste ou forme tabulaire

L'ensemble est représenté en listant tous les éléments qui le composent. Les éléments sont placés entre accolades et séparés par des virgules.

Example 1 - Ensemble de voyelles en alphabet anglais, $ A = \ lbrace a, e, i, o, u \ rbrace $

Example 2 - Ensemble de nombres impairs inférieurs à 10, $ B = \ lbrace 1,3,5,7,9 \ rbrace $

Définir la notation du générateur

L'ensemble est défini en spécifiant une propriété que les éléments de l'ensemble ont en commun. L'ensemble est décrit comme $ A = \ lbrace x: p (x) \ rbrace $

Example 1 - L'ensemble $ \ lbrace a, e, i, o, u \ rbrace $ s'écrit -

$ A = \ lbrace x: \ text {x est une voyelle en alphabet anglais} \ rbrace $

Example 2 - L'ensemble $ \ lbrace 1,3,5,7,9 \ rbrace $ s'écrit -

$ B = \ lbrace x: 1 \ le x \ lt 10 \ et \ (x \% 2) \ ne 0 \ rbrace $

Si un élément x est membre de tout ensemble S, il est noté $ x \ dans S $ et si un élément y n'est pas membre de l'ensemble S, il est noté $ y \ notin S $.

Example- Si $ S = \ lbrace1, 1.2, 1.7, 2 \ rbrace, 1 \ in S $ mais $ 1.5 \ notin S $

Quelques ensembles importants

N - l'ensemble de tous les nombres naturels = $ \ lbrace1, 2, 3, 4, ..... \ rbrace $

Z - l'ensemble de tous les entiers = $ \ lbrace ....., -3, -2, -1, 0, 1, 2, 3, ..... \ rbrace $

Z⁺ - l'ensemble de tous les entiers positifs

Q - l'ensemble de tous les nombres rationnels

R - l'ensemble de tous les nombres réels

W - l'ensemble de tous les nombres entiers

Cardinalité d'un ensemble

La cardinalité d'un ensemble S, notée $ | S | $, est le nombre d'éléments de l'ensemble. Le nombre est également appelé nombre cardinal. Si un ensemble a un nombre infini d'éléments, sa cardinalité est $ \ infty $.

Example- $ | \ lbrace 1, 4, 3, 5 \ rbrace | = 4, | \ lbrace 1, 2, 3, 4, 5, \ points \ rbrace | = \ infty $

S'il y a deux ensembles X et Y,

$ | X | = | Y | $ désigne deux ensembles X et Y ayant la même cardinalité. Cela se produit lorsque le nombre d'éléments dans X est exactement égal au nombre d'éléments dans Y. Dans ce cas, il existe une fonction bijective 'f' de X à Y.
$ | X | \ le | Y | $ indique que la cardinalité de l'ensemble X est inférieure ou égale à la cardinalité de l'ensemble Y. Il se produit lorsque le nombre d'éléments dans X est inférieur ou égal à celui de Y. Ici, il existe une fonction injective 'f' de X à Y.
$ | X | \ lt | Y | $ indique que la cardinalité de l'ensemble X est inférieure à la cardinalité de l'ensemble Y. Cela se produit lorsque le nombre d'éléments dans X est inférieur à celui de Y. Ici, la fonction 'f' de X à Y est une fonction injective mais pas bijective.
$ Si \ | X | \ le | Y | $ et $ | X | \ ge | Y | $ puis $ | X | = | Y | $. Les ensembles X et Y sont communément appelés ensembles équivalents.

Types d'ensembles

Les ensembles peuvent être classés en plusieurs types. Certains d'entre eux sont finis, infinis, sous-ensemble, universels, propres, singleton, etc.

Ensemble fini

Un ensemble qui contient un nombre défini d'éléments est appelé un ensemble fini.

Example- $ S = \ lbrace x \: | \: x \ in N $ et 70 $ \ gt x \ gt 50 \ rbrace $

Ensemble infini

Un ensemble qui contient un nombre infini d'éléments est appelé un ensemble infini.

Example- $ S = \ lbrace x \: | \: x \ dans N $ et $ x \ gt 10 \ rbrace $

Sous-ensemble

Un ensemble X est un sous-ensemble de l'ensemble Y (écrit comme $ X \ subseteq Y $) si chaque élément de X est un élément de l'ensemble Y.

Example 1- Soit, $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ et $ Y = \ lbrace 1, 2 \ rbrace $. Ici, l'ensemble Y est un sous-ensemble de l'ensemble X car tous les éléments de l'ensemble Y sont dans l'ensemble X. On peut donc écrire $ Y \ subseteq X $.

Example 2- Soit, $ X = \ lbrace 1, 2, 3 \ rbrace $ et $ Y = \ lbrace 1, 2, 3 \ rbrace $. Ici, l'ensemble Y est un sous-ensemble (pas un sous-ensemble propre) de l'ensemble X car tous les éléments de l'ensemble Y sont dans l'ensemble X. On peut donc écrire $ Y \ subseteq X $.

Sous-ensemble approprié

Le terme «sous-ensemble propre» peut être défini comme «sous-ensemble de mais non égal à». Un ensemble X est un sous-ensemble propre de l'ensemble Y (écrit comme $ X \ sous-ensemble Y $) si chaque élément de X est un élément de l'ensemble Y et $ | X | \ lt | Y | $.

Example- Soit, $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ et $ Y = \ lbrace 1, 2 \ rbrace $. Ici, ensemble $ Y \ sous-ensemble X $ puisque tous les éléments de $ Y $ sont également contenus dans $ X $ et $ X $ a au moins un élément est plus que l'ensemble $ Y $.

Ensemble universel

C'est une collection de tous les éléments dans un contexte ou une application particulière. Tous les ensembles dans ce contexte ou cette application sont essentiellement des sous-ensembles de cet ensemble universel. Les ensembles universels sont représentés par $ U $.

Example- Nous pouvons définir $ U $ comme l'ensemble de tous les animaux sur terre. Dans ce cas, l'ensemble de tous les mammifères est un sous-ensemble de $ U $, l'ensemble de tous les poissons est un sous-ensemble de $ U $, l'ensemble de tous les insectes est un sous-ensemble de $ U $, et ainsi de suite.

Ensemble vide ou ensemble nul

Un ensemble vide ne contient aucun élément. Il est noté $ \ emptyset $. Comme le nombre d'éléments dans un ensemble vide est fini, l'ensemble vide est un ensemble fini. La cardinalité d'un ensemble vide ou d'un ensemble nul est zéro.

Example- $ S = \ lbrace x \: | \: x \ in N $ et $ 7 \ lt x \ lt 8 \ rbrace = \ emptyset $

Ensemble singleton ou ensemble d'unité

L'ensemble de singleton ou l'ensemble d'unités ne contient qu'un seul élément. Un ensemble de singleton est noté $ \ lbrace s \ rbrace $.

Example- $ S = \ lbrace x \: | \: x \ dans N, \ 7 \ lt x \ lt 9 \ rbrace $ = $ \ lbrace 8 \ rbrace $

Ensemble égal

Si deux ensembles contiennent les mêmes éléments, ils sont dits égaux.

Example - Si $ A = \ lbrace 1, 2, 6 \ rbrace $ et $ B = \ lbrace 6, 1, 2 \ rbrace $, ils sont égaux car chaque élément de l'ensemble A est un élément de l'ensemble B et chaque élément de l'ensemble B est un élément de l'ensemble A.

Ensemble équivalent

Si les cardinalités de deux ensembles sont identiques, elles sont appelées ensembles équivalents.

Example- Si $ A = \ lbrace 1, 2, 6 \ rbrace $ et $ B = \ lbrace 16, 17, 22 \ rbrace $, ils sont équivalents car la cardinalité de A est égale à la cardinalité de B. ie $ | A | = | B | = 3 $

Ensemble de chevauchement

Deux ensembles qui ont au moins un élément commun sont appelés ensembles se chevauchant.

En cas de chevauchement des ensembles -

$ n (A \ coupe B) = n (A) + n (B) - n (A \ cap B) $
$ n (A \ coupe B) = n (A - B) + n (B - A) + n (A \ cap B) $
$ n (A) = n (A - B) + n (A \ cap B) $
$ n (B) = n (B - A) + n (A \ cap B) $

Example- Soit, $ A = \ lbrace 1, 2, 6 \ rbrace $ et $ B = \ lbrace 6, 12, 42 \ rbrace $. Il y a un élément commun «6», donc ces ensembles sont des ensembles qui se chevauchent.

Ensemble disjoint

Deux ensembles A et B sont appelés ensembles disjoints s'ils n'ont même pas un élément en commun. Par conséquent, les ensembles disjoints ont les propriétés suivantes -

$ n (A \ cap B) = \ emptyset $
$ n (A \ coupe B) = n (A) + n (B) $

Example - Soit, $ A = \ lbrace 1, 2, 6 \ rbrace $ et $ B = \ lbrace 7, 9, 14 \ rbrace $, il n'y a pas un seul élément commun, donc ces ensembles sont des ensembles qui se chevauchent.

Diagrammes de Venn

Le diagramme de Venn, inventé en 1880 par John Venn, est un diagramme schématique qui montre toutes les relations logiques possibles entre différents ensembles mathématiques.

Examples

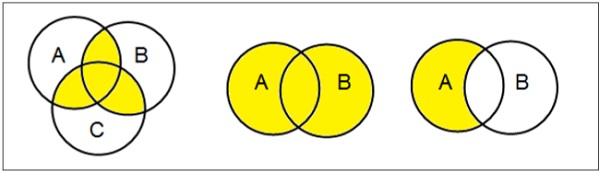
Définir les opérations

Les opérations d'ensemble incluent l'union d'ensemble, l'intersection d'ensemble, la différence d'ensemble, le complément d'ensemble et le produit cartésien.

Définir l'union

L'union des ensembles A et B (notée $ A \ cup B $) est l'ensemble des éléments qui sont dans A, dans B, ou à la fois dans A et B. Par conséquent, $ A \ cup B = \ lbrace x \: | \: x \ dans A \ OU \ x \ dans B \ rbrace $.

Example- Si $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ et B = $ \ lbrace 13, 14, 15 \ rbrace $, alors $ A \ cup B = \ lbrace 10, 11, 12, 13, 14 , 15 \ rbrace $. (L'élément commun n'apparaît qu'une seule fois)

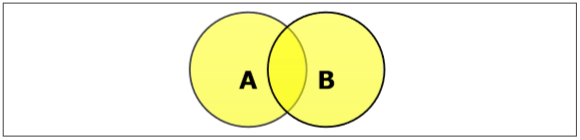
Définir l'intersection

L'intersection des ensembles A et B (notée $ A \ cap B $) est l'ensemble des éléments qui sont à la fois dans A et B. Par conséquent, $ A \ cap B = \ lbrace x \: | \: x \ in A \ AND \ x \ dans B \ rbrace $.

Example - Si $ A = \ lbrace 11, 12, 13 \ rbrace $ et $ B = \ lbrace 13, 14, 15 \ rbrace $, alors $ A \ cap B = \ lbrace 13 \ rbrace $.

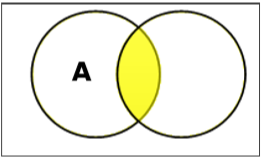
Définir la différence / complément relatif

La différence d'ensemble des ensembles A et B (notée $ A - B $) est l'ensemble des éléments qui sont uniquement dans A mais pas dans B. Par conséquent, $ A - B = \ lbrace x \: | \: x \ dans A \ AND \ x \ notin B \ rbrace $.

Example- Si $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ et $ B = \ lbrace 13, 14, 15 \ rbrace $, alors $ (A - B) = \ lbrace 10, 11, 12 \ rbrace $ et $ (B - A) = \ lbrace 14, 15 \ rbrace $. Ici, nous pouvons voir $ (A - B) \ ne (B - A) $

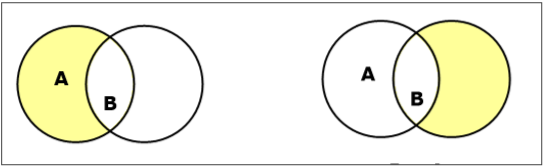
Complément d'un ensemble

Le complément d'un ensemble A (noté $ A '$) est l'ensemble des éléments qui ne sont pas dans l'ensemble A. Par conséquent, $ A' = \ lbrace x | x \ notin A \ rbrace $.

Plus précisément, $ A '= (U - A) $ où $ U $ est un ensemble universel qui contient tous les objets.

Example- Si $ A = \ lbrace x \: | \: x \ \: {appartient \: to \: set \: of \: odd \: integers} \ rbrace $ then $ A '= \ lbrace y \: | \: y \ \: {n'appartient \: pas \: \: à \: set \: of \: odd \: integers} \ rbrace $

Produit cartésien / produit croisé

Le produit cartésien de n nombre d'ensembles $ A_1, A_2, \ points A_n $ notés $ A_1 \ fois A_2 \ points \ fois A_n $ peut être défini comme toutes les paires ordonnées possibles $ (x_1, x_2, \ points x_n) $ où $ x_1 \ dans A_1, x_2 \ dans A_2, \ points x_n \ dans A_n $

Example - Si nous prenons deux ensembles $ A = \ lbrace a, b \ rbrace $ et $ B = \ lbrace 1, 2 \ rbrace $,

Le produit cartésien de A et B s'écrit - $ A \ times B = \ lbrace (a, 1), (a, 2), (b, 1), (b, 2) \ rbrace $

Le produit cartésien de B et A s'écrit - $ B \ times A = \ lbrace (1, a), (1, b), (2, a), (2, b) \ rbrace $

Ensemble de puissance

L'ensemble de puissance d'un ensemble S est l'ensemble de tous les sous-ensembles de S, y compris l'ensemble vide. La cardinalité d'un ensemble de puissances d'un ensemble S de cardinalité n est $ 2 ^ n $. L'ensemble de puissance est noté $ P (S) $.

Example −

Pour un ensemble $ S = \ lbrace a, b, c, d \ rbrace $ calculons les sous-ensembles -

Sous-ensembles avec 0 élément - $ \ lbrace \ emptyset \ rbrace $ (l'ensemble vide)
Sous-ensembles avec 1 élément - $ \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace $
Sous-ensembles avec 2 éléments - $ \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace $
Sous-ensembles avec 3 éléments - $ \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace $
Sous-ensembles avec 4 éléments - $ \ lbrace a, b, c, d \ rbrace $

Par conséquent, $ P (S) = $

$ \ lbrace \ quad \ lbrace \ emptyset \ rbrace, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace, \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace, \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace a, b, c, d \ rbrace \ quad \ rbrace $

$ | P (S) | = 2 ^ 4 = 16 $

Note - L'ensemble de puissance d'un ensemble vide est également un ensemble vide.

$ | P (\ lbrace \ emptyset \ rbrace) | = 2 ^ 0 = 1 $

Partitionnement d'un ensemble

La partition d'un ensemble, disons S , est une collection de n sous-ensembles disjoints, disons $ P_1, P_2, \ points P_n $ qui satisfait les trois conditions suivantes -

$ P_i $ ne contient pas l'ensemble vide.

$ \ lbrack P_i \ ne \ lbrace \ emptyset \ rbrace \ for \ all \ 0 \ lt i \ le n \ rbrack $
L'union des sous-ensembles doit être égale à l'ensemble d'origine.

$ \ lbrack P_1 \ cup P_2 \ cup \ dots \ cup P_n = S \ rbrack $
L'intersection de deux ensembles distincts est vide.

$ \ lbrack P_a \ cap P_b = \ lbrace \ emptyset \ rbrace, \ for \ a \ ne b \ where \ n \ ge a, \: b \ ge 0 \ rbrack $

Example

Soit $ S = \ lbrace a, b, c, d, e, f, g, h \ rbrace $

Un partitionnement probable est $ \ lbrace a \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $

Un autre partitionnement probable est $ \ lbrace a, b \ rbrace, \ lbrace c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $