Mathématiques discrètes - Arbres couvrant
Un arbre couvrant d'un graphe non orienté connecté $ G $ est un arbre qui inclut au minimum tous les sommets de $ G $. Un graphique peut avoir de nombreux arbres couvrant.
Exemple
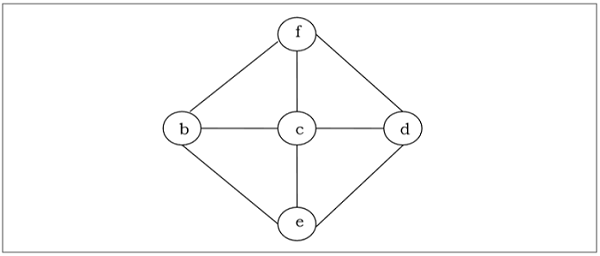
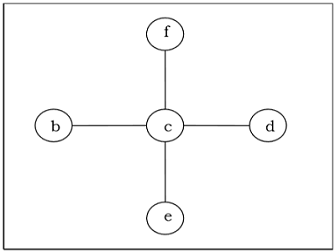
Arbre couvrant minimum
Un arbre couvrant avec un poids assigné inférieur ou égal au poids de chaque arbre couvrant possible d'un graphe pondéré, connecté et non orienté $ G $, il est appelé arbre couvrant minimum (MST). Le poids d'un arbre couvrant est la somme de tous les poids attribués à chaque arête de l'arbre couvrant.
Exemple
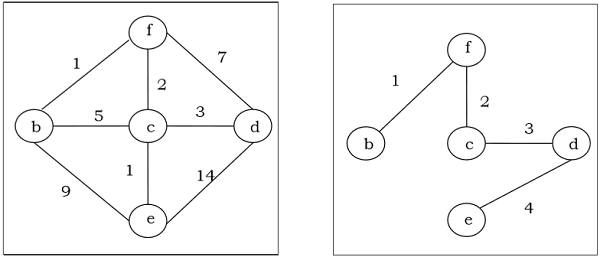
Algorithme de Kruskal
L'algorithme de Kruskal est un algorithme glouton qui trouve un arbre couvrant minimum pour un graphe pondéré connecté. Il trouve un arbre de ce graphe qui inclut chaque sommet et le poids total de toutes les arêtes de l'arbre est inférieur ou égal à chaque arbre couvrant possible.
Algorithme
Step 1 - Disposer toutes les arêtes du graphe donné $ G (V, E) $ dans l'ordre croissant selon leur poids d'arête.
Step 2 - Choisissez le plus petit bord pondéré du graphique et vérifiez s'il forme un cycle avec l'arbre couvrant formé jusqu'à présent.
Step 3 - S'il n'y a pas de cycle, incluez cette arête dans l'arbre couvrant, sinon supprimez-la.
Step 4 - Répétez les étapes 2 et 3 jusqu'à ce que $ (V-1) $ nombre d'arêtes soient laissées dans l'arbre couvrant.
Problem
Supposons que nous voulions trouver un arbre couvrant minimum pour le graphe G suivant en utilisant l'algorithme de Kruskal.
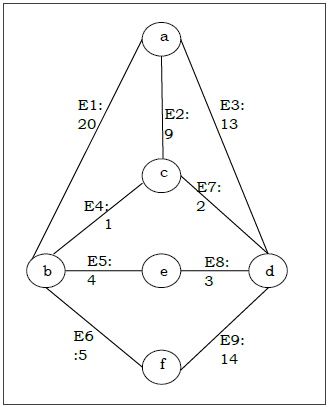
Solution
À partir du graphique ci-dessus, nous construisons le tableau suivant -
| Bord No. | Paire de sommets | Poids du bord |
|---|---|---|
| E1 | (un B) | 20 |
| E2 | (a, c) | 9 |
| E3 | (un d) | 13 |
| E4 | (avant JC) | 1 |
| E5 | (être) | 4 |
| E6 | (b, f) | 5 |
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E9 | (d, f) | 14 |
Maintenant, nous allons réorganiser le tableau dans l'ordre croissant par rapport au poids du bord -
| Bord No. | Paire de sommets | Poids du bord |
|---|---|---|
| E4 | (avant JC) | 1 |
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E5 | (être) | 4 |
| E6 | (b, f) | 5 |
| E2 | (a, c) | 9 |
| E3 | (un d) | 13 |
| E9 | (d, f) | 14 |
| E1 | (un B) | 20 |
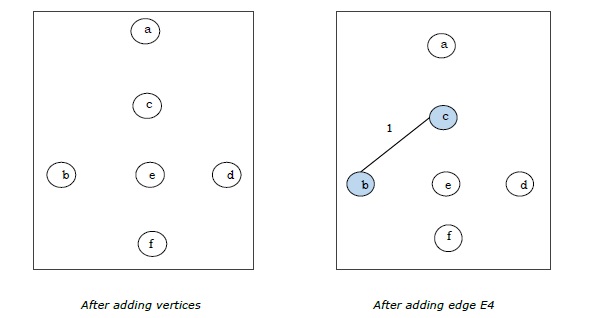
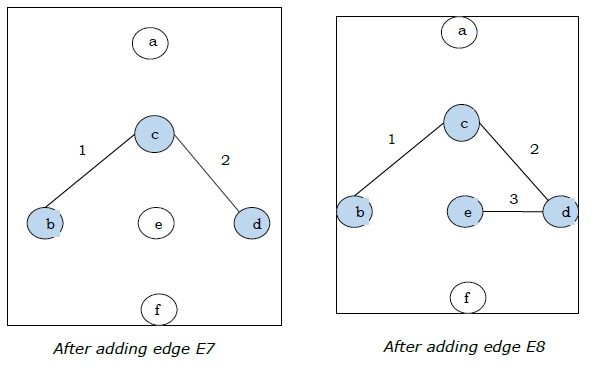
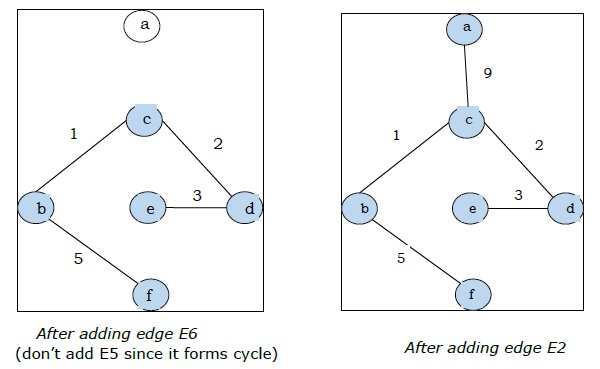
Puisque nous avons tous les 5 arêtes dans la dernière figure, nous arrêtons l'algorithme et c'est l'arbre couvrant minimal et son poids total est $ (1 + 2 + 3 + 5 + 9) = 20 $.
Algorithme de Prim
L'algorithme de Prim, découvert en 1930 par des mathématiciens, Vojtech Jarnik et Robert C. Prim, est un algorithme glouton qui trouve un arbre couvrant minimum pour un graphe pondéré connecté. Il trouve un arbre de ce graphe qui inclut chaque sommet et le poids total de toutes les arêtes de l'arbre est inférieur ou égal à chaque arbre couvrant possible. L'algorithme de Prim est plus rapide sur les graphes denses.
Algorithme
Initialisez l'arbre couvrant minimal avec un seul sommet, choisi au hasard dans le graphique.
Répétez les étapes 3 et 4 jusqu'à ce que tous les sommets soient inclus dans l'arborescence.
Sélectionnez une arête qui relie l'arbre à un sommet qui n'est pas encore dans l'arbre, de sorte que le poids de l'arête soit minimal et que l'inclusion de l'arête ne forme pas un cycle.
Ajoutez l'arête sélectionnée et le sommet qu'elle relie à l'arbre.
Problem
Supposons que nous voulions trouver un arbre couvrant minimum pour le graphe G suivant en utilisant l'algorithme de Prim.
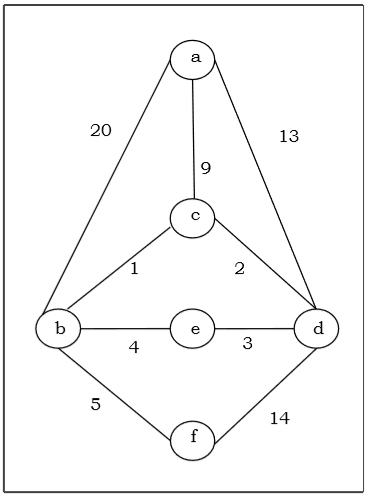
Solution
Ici, nous commençons par le sommet «a» et procédons.
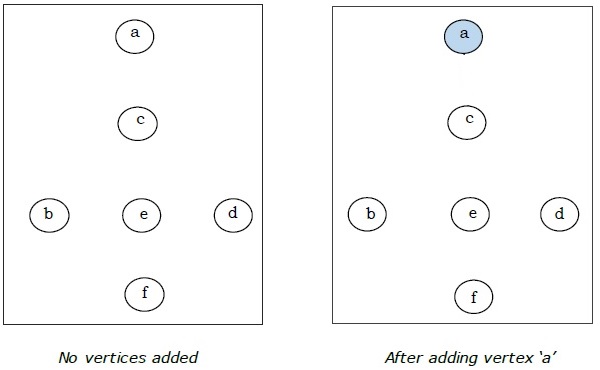
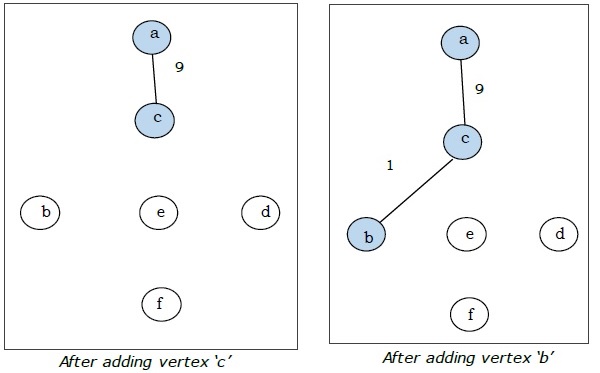
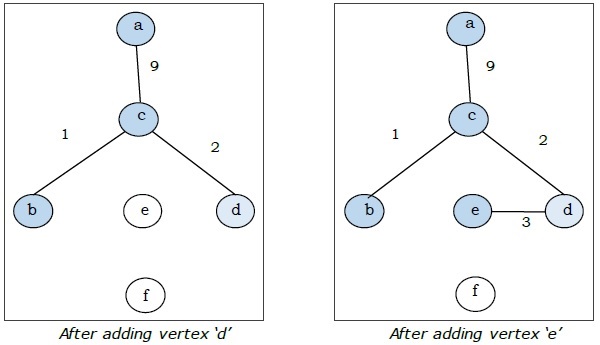
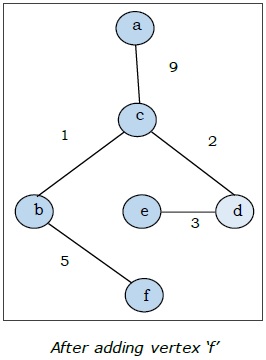
Il s'agit de l'arbre couvrant minimal et son poids total est de $ (1 + 2 + 3 + 5 + 9) = 20 $.