Simplification des fonctions booléennes
Simplification à l'aide de fonctions algébriques
Dans cette approche, une expression booléenne est réduite en une expression équivalente en appliquant des identités booléennes.
Problème 1
Réduisez l'expression booléenne suivante à l'aide d'identités booléennes -
$$ F (A, B, C) = A'B + BC '+ BC + AB'C' $$
Solution
Soit, $ F (A, B, C) = A'B + BC '+ BC + AB'C' $
Ou, $ F (A, B, C) = A'B + (BC '+ BC') + BC + AB'C '$
[Par loi idempotente, BC '= BC' + BC ']
Ou, $ F (A, B, C) = A'B + (BC '+ BC) + (BC' + AB'C ') $
Ou, $ F (A, B, C) = A'B + B (C '+ C) + C' (B + AB ') $
[Par les lois distributives]
Ou, $ F (A, B, C) = A'B + B.1 + C '(B + A) $
[(C '+ C) = 1 et loi d'absorption (B + AB') = (B + A)]
Ou, $ F (A, B, C) = A'B + B + C '(B + A) $
[B.1 = B]
Ou, $ F (A, B, C) = B (A '+ 1) + C' (B + A) $
Ou, $ F (A, B, C) = B.1 + C '(B + A) $
[(A '+ 1) = 1]
Ou, $ F (A, B, C) = B + C '(B + A) $
[Comme, B.1 = B]
Ou, $ F (A, B, C) = B + BC '+ AC' $
Ou, $ F (A, B, C) = B (1 + C ') + AC' $
Ou, $ F (A, B, C) = B.1 + AC '$
[Comme, (1 + C ') = 1]
Ou, $ F (A, B, C) = B + AC '$
[Comme, B.1 = B]
Ainsi, $ F (A, B, C) = B + AC '$ est la forme minimisée.
Problème 2
Réduisez l'expression booléenne suivante à l'aide d'identités booléennes -
$$ F (A, B, C) = (A + B) (A + C) $$
Solution
Étant donné, $ F (A, B, C) = (A + B) (A + C) $
Ou, $ F (A, B, C) = AA + AC + BA + BC $ [Application de la règle distributive]
Ou, $ F (A, B, C) = A + AC + BA + BC $ [Application de la loi idempotente]
Ou, $ F (A, B, C) = A (1 + C) + BA + BC $ [Application de la loi distributive]
Ou, $ F (A, B, C) = A + BA + BC $ [Application de la loi de dominance]
Ou, $ F (A, B, C) = (A + 1) .A + BC $ [Application de la loi distributive]
Ou, $ F (A, B, C) = 1.A + BC $ [Application de la loi de dominance]
Ou, $ F (A, B, C) = A + BC $ [Application de la loi de dominance]
Ainsi, $ F (A, B, C) = A + BC $ est la forme minimisée.
Cartes de Karnaugh
La carte de Karnaugh (K – map), introduite par Maurice Karnaughin en 1953, est une représentation en grille d'une table de vérité qui est utilisée pour simplifier les expressions d'algèbre booléenne. Une carte de Karnaugh a zéro et une entrées à des positions différentes. Il permet de regrouper des expressions booléennes avec des facteurs communs et d'éliminer les variables indésirables de l'expression. Dans une K-map, le franchissement d'une limite de cellule verticale ou horizontale est toujours un changement d'une seule variable.
Exemple 1
Une table de vérité arbitraire est prise ci-dessous -
| UNE | B | Une opération B |
|---|---|---|
| 0 | 0 | w |
| 0 | 1 | X |
| 1 | 0 | y |
| 1 | 1 | z |
Maintenant, nous allons créer une k-map pour la table de vérité ci-dessus -

Exemple 2
Nous allons maintenant faire une K-map pour l'expression - AB + A'B '
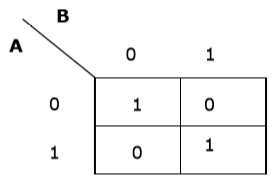
Simplification à l'aide de K-map
K-map utilise certaines règles pour simplifier les expressions booléennes en combinant les cellules adjacentes en un seul terme. Les règles sont décrites ci-dessous -
Rule 1 - Toute cellule contenant un zéro ne peut pas être groupée.
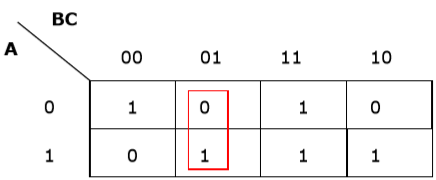
Mauvais regroupement
Rule 2 - Les groupes doivent contenir 2n cellules (n à partir de 1).
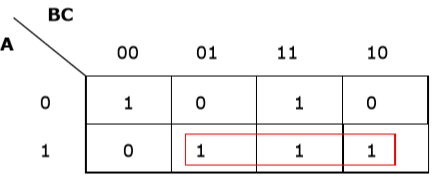
Mauvais regroupement
Rule 3 - Le groupement doit être horizontal ou vertical, mais ne doit pas être diagonal.
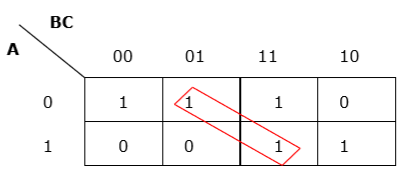
Mauvais regroupement diagonal
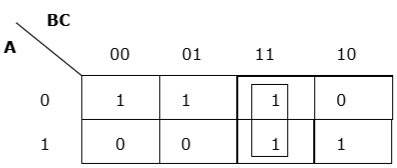
Regroupement vertical approprié
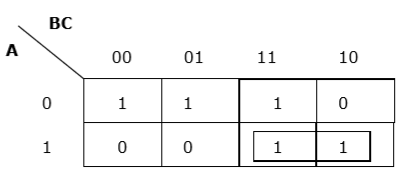
Regroupement horizontal approprié
Rule 4 - Les groupes doivent être couverts le plus largement possible.
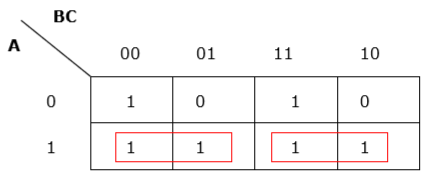
Regroupement insuffisant
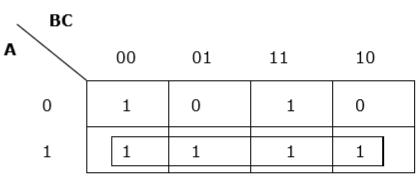
Regroupement approprié
Rule 5 - Si l'une des cellules ne peut être regroupée avec aucune autre cellule, elle agira comme un groupe lui-même.
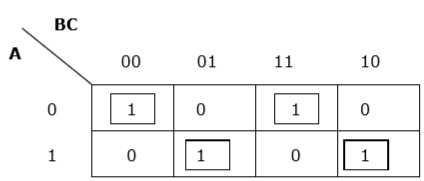
Regroupement approprié
Rule 6 - Les groupes peuvent se chevaucher, mais il devrait y avoir le moins de groupes possible.
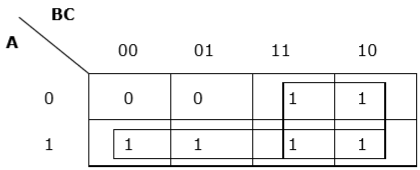
Regroupement approprié
Rule 7 - La ou les cellules les plus à gauche peuvent être regroupées avec la / les cellules les plus à droite et la / les cellules les plus hautes peuvent être regroupées avec la / les cellules les plus basses.
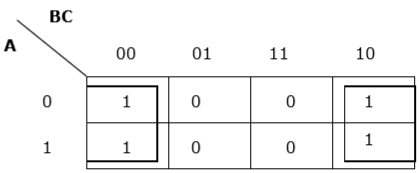
Regroupement approprié
Problème
Réduisez l'expression booléenne suivante à l'aide de K-map -
$$ F (A, B, C) = A'BC + A'BC '+ AB'C' + AB'C $$
Solution
Chaque terme est mis dans k-map et nous obtenons ce qui suit -
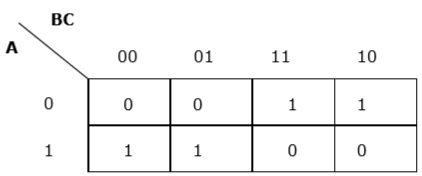
K-map pour F (A, B, C)
Maintenant, nous allons regrouper les cellules de 1 selon les règles énoncées ci-dessus -
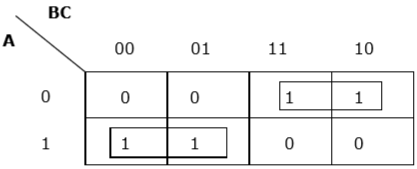
K-map pour F (A, B, C)
Nous avons deux groupes appelés $ A'B $ et $ AB '$. Par conséquent, $ F (A, B, C) = A'B + AB '= A \ oplus B $. C'est la forme minimisée.