Introduction aux arbres

Treeest une structure discrète qui représente des relations hiérarchiques entre des éléments ou des nœuds individuels. Un arbre dans lequel un parent n'a pas plus de deux enfants est appelé un arbre binaire.

L'arbre et ses propriétés

Definition- Un arbre est un graphe non orienté acyclique connexe. Il existe un chemin unique entre chaque paire de sommets dans $ G $. Un arbre avec N nombre de sommets contient $ (N-1) $ nombre d'arêtes. Le sommet qui est de 0 degré est appelé racine de l'arbre. Le sommet qui est de 1 degré est appelé nœud feuille de l'arbre et le degré d'un nœud interne est au moins 2.

Example - Ce qui suit est un exemple d'arbre -

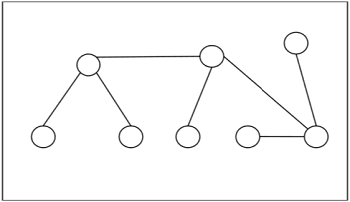
Centres et bi-centres d'un arbre

Le centre d'un arbre est un sommet avec une excentricité minimale. L'excentricité d'un sommet $ X $ dans un arbre $ G $ est la distance maximale entre le sommet $ X $ et tout autre sommet de l'arbre. L'excentricité maximale est le diamètre de l'arbre. Si un arbre n'a qu'un seul centre, il est appelé Arbre central et si un arbre n'a que plus d'un centre, il est appelé Arbre bi-central. Chaque arbre est central ou bi-central.

Algorithme pour trouver les centres et bi-centres d'un arbre

Step 1 - Supprimez tous les sommets de degré 1 de l'arbre donné et supprimez également leurs arêtes incidentes.

Step 2- Répétez l'étape 1 jusqu'à ce qu'il reste un seul sommet ou deux sommets joints par une arête. Si un seul sommet est laissé, c'est le centre de l'arbre et si deux sommets joints par une arête sont laissés, alors c'est le bi-centre de l'arbre.

Problem 1

Découvrez le centre / bi-centre de l'arbre suivant -

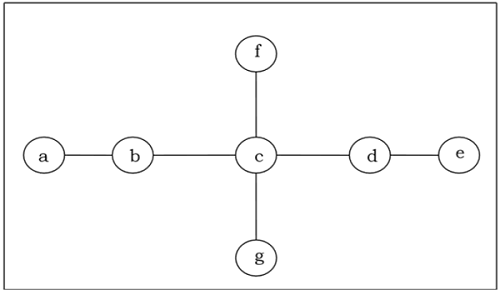
Solution

Dans un premier temps, nous allons supprimer tous les sommets de degré 1 et également supprimer leurs arêtes incidentes et obtenir l'arbre suivant -

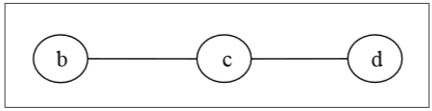
Encore une fois, nous allons supprimer tous les sommets de degré 1 et également supprimer leurs arêtes incidentes et obtenir l'arbre suivant -

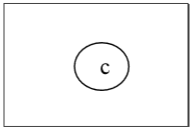
Enfin, nous avons un seul sommet 'c' et nous arrêtons l'algorithme. Comme il n'y a qu'un seul sommet, cet arbre a un centre «c» et l'arbre est un arbre central.

Problem 2

Découvrez le centre / bi-centre de l'arbre suivant -

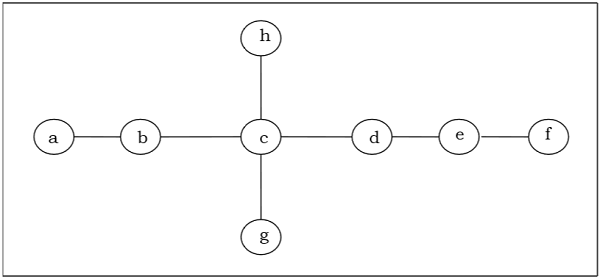
Solution

Dans un premier temps, nous allons supprimer tous les sommets de degré 1 et également supprimer leurs arêtes incidentes et obtenir l'arbre suivant -

Encore une fois, nous allons supprimer tous les sommets de degré 1 et également supprimer leurs arêtes incidentes et obtenir l'arbre suivant -

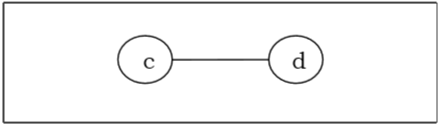
Enfin, nous avons deux sommets «c» et «d» à gauche, donc nous arrêtons l'algorithme. Comme deux sommets joints par une arête sont laissés, cet arbre a un 'cd' bi-centre et l'arbre est bi-central.

Arbres étiquetés

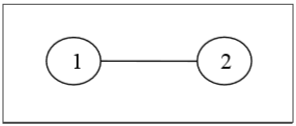
Definition- Un arbre étiqueté est un arbre dont les sommets reçoivent des numéros uniques de 1 à n. Nous pouvons compter ces arbres pour de petites valeurs de n à la main afin de conjecturer une formule générale. Le nombre d'arbres étiquetés de n nombre de sommets est $ n ^ {n-2} $. Deux arbres étiquetés sont isomorphes si leurs graphes sont isomorphes et les points correspondants des deux arbres ont les mêmes étiquettes.

Exemple

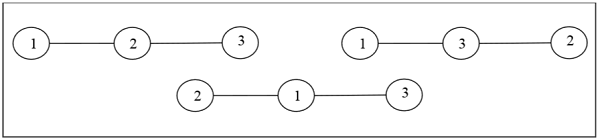
Arbres sans étiquette

Definition- Un arbre non étiqueté est un arbre dont les sommets ne reçoivent aucun numéro. Le nombre d'arbres étiquetés de n nombre de sommets est $ \ frac {(2n)!} {(N + 1)! N! } $ (n ^ième numéro catalan)

Exemple

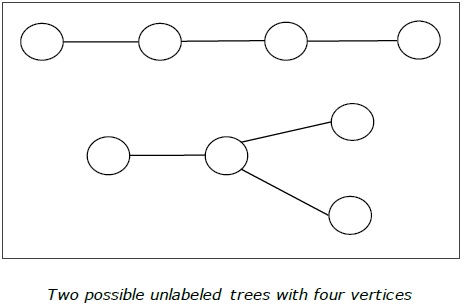
Arbre enraciné

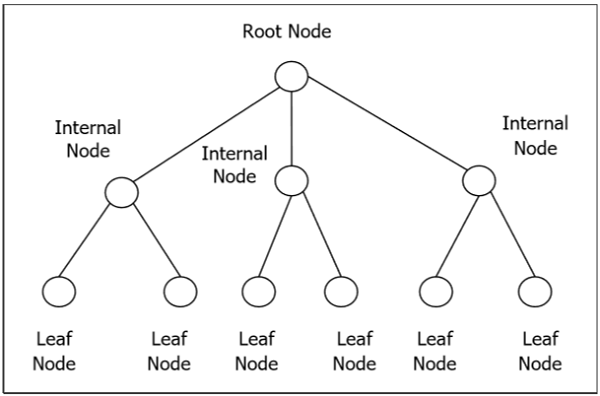
Un arbre enraciné $ G $ est un graphe acyclique connecté avec un nœud spécial appelé racine de l'arbre et chaque arête provient directement ou indirectement de la racine. Un arbre enraciné ordonné est un arbre enraciné où les enfants de chaque sommet interne sont ordonnés. Si chaque sommet interne d'un arbre enraciné n'a pas plus de m enfants, on l'appelle un arbre m-aire. Si chaque sommet interne d'un arbre enraciné a exactement m enfants, on l'appelle un arbre m-aire complet. Si $ m = 2 $, l'arbre enraciné est appelé un arbre binaire.

Arbre de recherche binaire

L'arbre de recherche binaire est un arbre binaire qui satisfait la propriété suivante -

$ X $ dans le sous-arbre gauche du sommet $ V, Value (X) \ le Value (V) $
$ Y $ dans le sous-arbre droit du sommet $ V, Value (Y) \ ge Value (V) $

Ainsi, la valeur de tous les sommets du sous-arbre gauche d'un nœud interne $ V $ est inférieure ou égale à $ V $ et la valeur de tous les sommets du sous-arbre droit du nœud interne $ V $ sont supérieurs ou égaux à $ V $. Le nombre de liens entre le nœud racine et le nœud le plus profond correspond à la hauteur de l'arborescence de recherche binaire.

Exemple

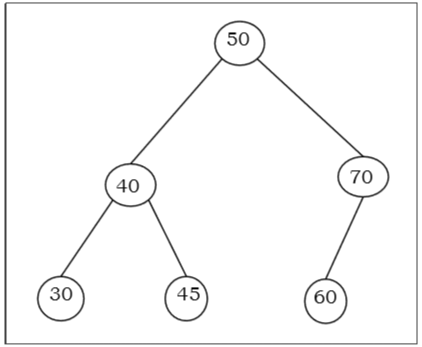
Algorithme pour rechercher une clé dans BST

BST_Search(x, k) 
if ( x = NIL or k = Value[x] ) 
   return x; 
if ( k < Value[x]) 
   return BST_Search (left[x], k); 
else  
   return BST_Search (right[x], k)

Complexité de l'arbre de recherche binaire

	Cas moyen	Pire cas
Complexité spatiale	Sur)	Sur)
Complexité de la recherche	O (log n)	Sur)
Complexité d'insertion	O (log n)	Sur)
Complexité de la suppression	O (log n)	Sur)