Mathématiques discrètes - En savoir plus sur les graphiques

Coloration graphique

La coloration du graphe est la procédure d'affectation de couleurs à chaque sommet d'un graphe G de telle sorte qu'aucun sommet adjacent n'obtienne la même couleur. L'objectif est de minimiser le nombre de couleurs lors de la coloration d'un graphique. Le plus petit nombre de couleurs requis pour colorer un graphique G est appelé son numéro chromatique de ce graphique. Le problème de coloration du graphique est un problème NP Complete.

Méthode pour colorer un graphique

Les étapes nécessaires pour colorer un graphe G avec n nombre de sommets sont les suivantes -

Step 1 - Organisez les sommets du graphe dans un certain ordre.

Step 2 - Choisissez le premier sommet et colorez-le avec la première couleur.

Step 3- Choisissez le sommet suivant et colorez-le avec la couleur numérotée la plus basse qui n'a été colorée sur aucun des sommets adjacents. Si tous les sommets adjacents sont colorés avec cette couleur, attribuez-lui une nouvelle couleur. Répétez cette étape jusqu'à ce que tous les sommets soient colorés.

Example

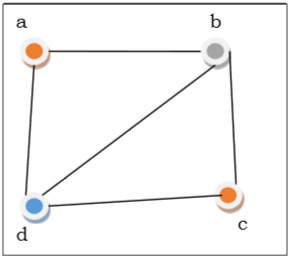
Dans la figure ci-dessus, au premier sommet $ a $ est coloré en rouge. Comme les sommets adjacents du sommet a sont à nouveau adjacents, le sommet $ b $ et le sommet $ d $ sont colorés avec une couleur différente, respectivement vert et bleu. Alors le sommet $ c $ est coloré en rouge car aucun sommet adjacent de $ c $ n'est coloré en rouge. Par conséquent, nous pourrions colorer le graphique de 3 couleurs. Par conséquent, le nombre chromatique du graphique est 3.

Applications de la coloration de graphes

Certaines applications de la coloration de graphes incluent -

Inscription de l'allocation
Coloration de la carte
Vérification de graphe bipartite
Attribution de fréquences radio mobiles
Faire un calendrier, etc.

Traversée graphique

Le parcours de graphe est le problème de la visite de tous les sommets d'un graphe dans un ordre systématique. Il existe principalement deux façons de parcourir un graphique.

Première recherche en largeur
Première recherche en profondeur

Première recherche en largeur

La première recherche en largeur (BFS) commence au sommet du niveau 0 de départ $ X $ du graphique $ G $. Ensuite, nous visitons tous les sommets voisins de $ X $. Après la visite, nous marquons les sommets comme «visités» et les plaçons au niveau 1. Ensuite, nous partons des sommets de niveau 1 et appliquons la même méthode sur chaque sommet de niveau 1 et ainsi de suite. Le parcours BFS se termine lorsque chaque sommet du graphe a été visité.

BFS Algorithm

Le concept est de visiter tous les sommets voisins avant de visiter d'autres sommets voisins des sommets voisins.

Initialisez le statut de tous les nœuds comme «Prêt».
Mettez le sommet source dans une file d'attente et changez son état en «En attente».
Répétez les deux étapes suivantes jusqu'à ce que la file d'attente soit vide -
- Supprimez le premier sommet de la file d'attente et marquez-le comme «Visité».
- Ajoutez à l'arrière de la file d'attente tous les voisins du sommet supprimé dont l'état est «Prêt». Marquez leur statut comme «En attente».

Problem

Prenons un graphe (le sommet source est 'a') et appliquons l'algorithme BFS pour connaître l'ordre de parcours.

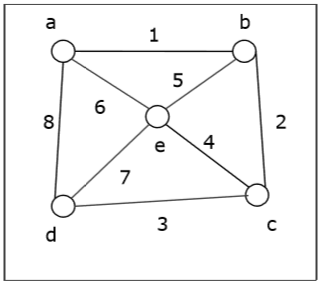
Solution -

Initialisez le statut de tous les sommets sur «Prêt».
Mettez un en file d'attente et changez son statut en «En attente».
Retirez un de la file d'attente, marquez-le comme «Visité».
Ajouter un état de voisins « Prêt » b, d et e à la fin de file d' attente et les marquer comme « en attente ».
Retirez b de la file d'attente, marquez-le comme «Visité», placez son voisin «Prêt» c à la fin de la file d'attente et marquez c comme «En attente».
Supprimez d de la file d'attente et marquez-le comme «Visité». Il n'a aucun voisin à l'état «Prêt».
Supprimez e de la file d'attente et marquez-le comme «Visité». Il n'a aucun voisin à l'état «Prêt».
Supprimez c de la file d'attente et marquez-le comme «Visité». Il n'a aucun voisin à l'état «Prêt».
La file d'attente est vide alors arrêtez.

Ainsi, l'ordre de parcours est -

$ a \ rightarrow b \ rightarrow d \ rightarrow e \ rightarrow c $

Les autres ordres de parcours sont -

$ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $

Ou, $ a \ rightarrow d \ rightarrow b \ rightarrow e \ rightarrow c $

Ou, $ a \ rightarrow e \ rightarrow b \ rightarrow d \ rightarrow c $

Ou, $ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $

Ou, $ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $

Application of BFS

Trouver le chemin le plus court
Arbre couvrant minimum pour un graphique non pondéré
Système de navigation GPS
Détection des cycles dans un graphe non orienté
Recherche de tous les nœuds dans un composant connecté

Complexity Analysis

Soit $ G (V, E) $ un graphe avec $ | V | $ nombre de sommets et $ | E | $ nombre d'arêtes. Si le premier algorithme de recherche en largeur visite chaque sommet du graphique et vérifie chaque arête, alors sa complexité temporelle serait -

$$ O (| V | + | E |). O (| E |) $$

Il peut varier entre $ O (1) $ et $ O (| V2 |) $

Première recherche en profondeur

L'algorithme de recherche en profondeur (DFS) commence à partir d'un sommet $ v $, puis il traverse son sommet adjacent (disons x) qui n'a pas été visité auparavant et marque comme "visité" et continue avec le sommet adjacent de $ x $ et bientôt.

Si à n'importe quel sommet, il rencontre que tous les sommets adjacents sont visités, alors il revient en arrière jusqu'à ce qu'il trouve le premier sommet ayant un sommet adjacent qui n'a pas été parcouru auparavant. Ensuite, il traverse ce sommet, continue avec ses sommets adjacents jusqu'à ce qu'il traverse tous les sommets visités et doive revenir en arrière. De cette façon, il traversera tous les sommets accessibles à partir du sommet initial $ v $.

DFS Algorithm

Le concept est de visiter tous les sommets voisins d'un sommet voisin avant de visiter les autres sommets voisins.

Initialiser l'état de tous les nœuds en tant que «Prêt»
Placez le sommet source dans une pile et changez son état en "En attente"
Répétez les deux étapes suivantes jusqu'à ce que la pile soit vide -
- Faites sortir le sommet supérieur de la pile et marquez-le comme "Visité"
- Poussez sur le haut de la pile tous les voisins du sommet supprimé dont l'état est «Prêt». Marquez leur statut comme «En attente».

Problem

Prenons un graphe (le sommet source est 'a') et appliquons l'algorithme DFS pour connaître l'ordre de parcours.

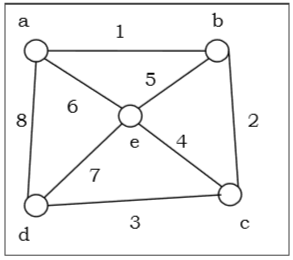
Solution

Initialisez le statut de tous les sommets sur «Prêt».
Poussez un dans la pile et changez son statut en «En attente».
Pop a et marquez-le comme "Visité".
Appuyez sur une des » voisins à l' état « Prêt » e, d et b en haut de la pile et les marquer comme « en attente ».
Sortez b de la pile, marquez-le comme «Visité», poussez son voisin «Prêt» c sur la pile.
Pop c de la pile et marquez-le comme «Visité». Il n'a pas de voisin «prêt».
Pop d de la pile et le marquer comme « visité ». Il n'a pas de voisin «prêt».
Pop e de la pile et le marquer comme « visité ». Il n'a pas de voisin «prêt».
La pile est vide. Alors arrêtez.

Ainsi, l'ordre de parcours est -

$ a \ rightarrow b \ rightarrow c \ rightarrow d \ rightarrow e $

Les autres ordres de parcours sont -

$ a \ rightarrow e \ rightarrow b \ rightarrow c \ rightarrow d $

Ou, $ a \ rightarrow b \ rightarrow e \ rightarrow c \ rightarrow d $

Ou, $ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $

Ou, $ a \ rightarrow d \ rightarrow c \ rightarrow e \ rightarrow b $

Ou, $ a \ rightarrow d \ rightarrow c \ rightarrow b \ rightarrow e $

Complexity Analysis

Soit $ G (V, E) $ un graphe avec $ | V | $ nombre de sommets et $ | E | $ nombre d'arêtes. Si l'algorithme DFS visite chaque sommet du graphique et vérifie chaque arête, alors la complexité temporelle est -

$$ \ circleddash (| V | + | E |) $$

Applications

Détection du cycle dans un graphique
Pour rechercher un tri topologique
Pour tester si un graphique est biparti
Recherche de composants connectés
Trouver les ponts d'un graphe
Trouver la bi-connectivité dans les graphiques
Résoudre le problème du Knight's Tour
Résoudre des énigmes avec une seule solution