Microwave Engineering - T-shirt d'avion EH
Une jonction EH Plane Tee est formée en attachant deux guides d'ondes simples, l'un parallèle et l'autre série, à un guide d'ondes rectangulaire qui a déjà deux ports. Ceci est également appelé commeMagic Tee, ou Hybrid ou 3dB coupler.
Les bras des guides d'ondes rectangulaires font deux ports appelés collinear ports c'est-à-dire, Port 1 et Port 2, tandis que le Port 3 est appelé H-Arm ou Sum port ou Parallel port. Le port 4 est appeléE-Arm ou Difference port ou Series port.
Les détails en coupe de Magic Tee peuvent être compris par la figure suivante.
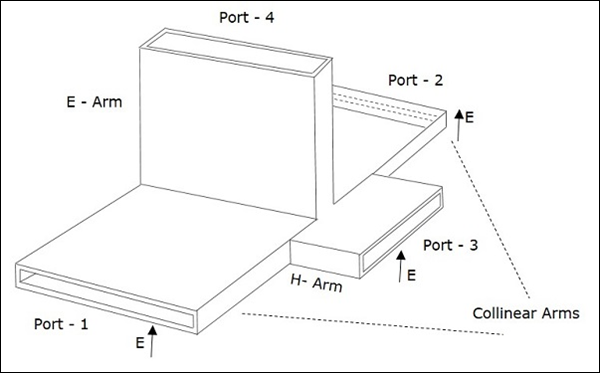
La figure suivante montre la connexion établie par les bras latéraux au guide d'ondes bidirectionnel pour former des ports parallèles et série.
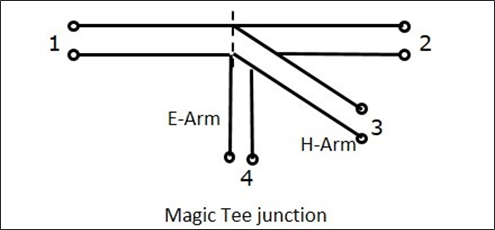
Caractéristiques de EH Plane Tee
Si un signal de phase et d'amplitude égales est envoyé au port 1 et au port 2, alors la sortie sur le port 4 est zéro et la sortie sur le port 3 sera l'additif des deux ports 1 et 2.
Si un signal est envoyé au port 4, (E-arm), la puissance est répartie entre les ports 1 et 2 de manière égale mais en phase opposée, alors qu'il n'y aurait pas de sortie au port 3. Par conséquent, $ S_ {34} $ = 0 .
Si un signal est alimenté au port 3, alors la puissance est répartie entre les ports 1 et 2 également, alors qu'il n'y aurait pas de sortie au port 4. Par conséquent, $ S_ {43} $ = 0.
Si un signal est fourni à l'un des ports colinéaires, alors il n'y a pas de sortie sur l'autre port colinéaire, car le bras électrique produit un retard de phase et le bras en H produit une avance de phase. Donc, $ S_ {12} $ = $ S_ {21} $ = 0.
Propriétés de EH Plane Tee
Les propriétés de EH Plane Tee peuvent être définies par sa matrice $ \ left [S \ right] _ {4 \ times 4} $.
C'est une matrice 4 × 4 car il y a 4 entrées possibles et 4 sorties possibles.
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} & S_ {14} \\ S_ {21} & S_ {22} & S_ {23} & S_ {24} \\ S_ {31} & S_ {32} & S_ {33} & S_ {34} \\ S_ {41} & S_ {42} & S_ {43} & S_ {44} \ end {bmatrix} $ ........ Equation 1
Comme il a la section H-Plane Tee
$ S_ {23} = S_ {13} $........ Equation 2
Comme il a la section E-Plane Tee
$ S_ {24} = -S_ {14} $........ Equation 3
Le port E-Arm et le port H-Arm sont tellement isolés que l'autre ne fournira pas de sortie, si une entrée est appliquée à l'un d'eux. Par conséquent, cela peut être noté comme
$ S_ {34} = S_ {43} = 0 $........ Equation 4
De la propriété de symétrie, nous avons
$ S_ {ij} = S_ {ji} $
$ S_ {12} = S_ {21}, S_ {13} = S_ {31}, S_ {14} = S_ {41} $
$ S_ {23} = S_ {32}, S_ {24} = S_ {42}, S_ {34} = S_ {43} $........ Equation 5
Si les ports 3 et 4 sont parfaitement adaptés à la jonction, alors
$ S_ {33} = S_ {44} = 0 $........ Equation 6
En substituant toutes les équations ci-dessus dans l'équation 1, pour obtenir la matrice $ [S] $,
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} & S_ {14} \\ S_ {12} & S_ {22} & S_ {13} & -S_ {14 } \\ S_ {13} & S_ {13} & 0 & 0 \\ S_ {14} & -S_ {14} & 0 & 0 \ end {bmatrix} $........ Equation 7
Depuis la propriété Unitary, $ [S] [S] ^ \ ast = [I] $
$ \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} & S_ {14} \\ S_ {12} & S_ {22} & S_ {13} & -S_ {14} \\ S_ {13} & S_ {13} & 0 & 0 \\ S_ {14} & -S_ {14} & 0 & 0 \ end {bmatrix} \ begin {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} & S_ {13} ^ {*} & S_ {14} ^ {*} \\ S_ {12} ^ {*} & S_ {22} ^ {*} & S_ {13} ^ {*} & -S_ {14} ^ {*} \\ S_ {13} & S_ {13} & 0 & 0 \\ S_ {14} & -S_ {14} & 0 & 0 \ end {bmatrix} $
$ = \ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $
$ R_1C_1: \ gauche | S_ {11} \ droite | ^ 2 + \ gauche | S_ {12} \ droite | ^ 2 + \ gauche | S_ {13} \ droite | ^ 2 = 1 + \ gauche | S_ {14} \ droite | ^ 2 = 1 $......... Equation 8
$ R_2C_2: \ gauche | S_ {12} \ droite | ^ 2 + \ gauche | S_ {22} \ droite | ^ 2 + \ gauche | S_ {13} \ droite | ^ 2 = 1 + \ gauche | S_ {14} \ droite | ^ 2 = 1 $......... Equation 9
$ R_3C_3: \ gauche | S_ {13} \ droite | ^ 2 + \ gauche | S_ {13} \ droite | ^ 2 = 1 $......... Equation 10
$ R_4C_4: \ gauche | S_ {14} \ droite | ^ 2 + \ gauche | S_ {14} \ droite | ^ 2 = 1 $......... Equation 11
À partir des équations 10 et 11, nous obtenons
$ S_ {13} = \ frac {1} {\ sqrt {2}} $........ Equation 12
$ S_ {14} = \ frac {1} {\ sqrt {2}} $........ Equation 13
En comparant les équations 8 et 9, nous avons
$ S_ {11} = S_ {22} $ ......... Equation 14
En utilisant ces valeurs des équations 12 et 13, nous obtenons
$ \ gauche | S_ {11} \ droite | ^ 2 + \ gauche | S_ {12} \ right | ^ 2 + \ frac {1} {2} + \ frac {1} {2} = 1 $
$ \ gauche | S_ {11} \ droite | ^ 2 + \ gauche | S_ {12} \ droite | ^ 2 = 0 $
$ S_ {11} = S_ {22} = 0 $ ......... Equation 15
De l'équation 9, nous obtenons $ S_ {22} = 0 $ ......... Equation 16
Nous comprenons maintenant que les ports 1 et 2 sont parfaitement adaptés à la jonction. Comme il s'agit d'une jonction à 4 ports, chaque fois que deux ports sont parfaitement adaptés, les deux autres ports sont également parfaitement adaptés à la jonction.
La jonction où les quatre ports sont parfaitement assortis s'appelle Magic Tee Junction.
En substituant les équations de 12 à 16, dans la matrice $ [S] $ de l'équation 7, on obtient la matrice de diffusion de Magic Tee comme
$$ [S] = \ begin {bmatrix} 0 & 0 & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ 0 & 0 & \ frac {1} {2} & - \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & \ frac {1} {\ sqrt {2}} & 0 & 0 \\ \ frac {1} {\ sqrt {2}} & - \ frac {1} {\ sqrt {2}} & 0 & 0 \ end {bmatrix} $$
Nous savons déjà que, $ [b] $ = $ [S] [a] $
En réécrivant ce qui précède, nous obtenons
$$ \ begin {vmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \ end {vmatrix} = \ begin {bmatrix} 0 & 0 & \ frac {1} {2} & \ frac {1} {\ sqrt {2} } \\ 0 & 0 & \ frac {1} {2} & - \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & \ frac {1} {\ sqrt {2}} & 0 & 0 \\ \ frac {1} {\ sqrt {2}} & - \ frac {1} {\ sqrt {2}} & 0 & 0 \ end {bmatrix} \ begin {vmatrix} a_1 \ \ a_2 \\ a_3 \\ a_4 \ end {vmatrix} $$
Applications de EH Plane Tee
Certaines des applications les plus courantes de EH Plane Tee sont les suivantes:
La jonction EH Plane est utilisée pour mesurer l'impédance - Un détecteur nul est connecté au port E-Arm tandis que la source hyperfréquence est connectée au port H-Arm. Les ports colinéaires avec ces ports forment un pont et la mesure de l'impédance est effectuée en équilibrant le pont.
EH Plane Tee est utilisé comme duplexeur - Un duplexeur est un circuit qui fonctionne à la fois comme émetteur et comme récepteur, en utilisant une seule antenne pour les deux fins. Les ports 1 et 2 sont utilisés comme récepteur et émetteur là où ils sont isolés et n'interféreront donc pas. L'antenne est connectée au port E-Arm. Une charge adaptée est connectée au port H-Arm, qui ne fournit aucune réflexion. Or, il existe une transmission ou une réception sans aucun problème.
EH Plane Tee est utilisé comme mélangeur - le port E-Arm est connecté à l'antenne et le port H-Arm est connecté à l'oscillateur local. Le port 2 a une charge adaptée qui n'a pas de réflexions et le port 1 a le circuit mélangeur, qui obtient la moitié de la puissance du signal et la moitié de la puissance de l'oscillateur pour produire la fréquence IF.
En plus des applications ci-dessus, une jonction EH Plane Tee est également utilisée comme pont micro-ondes, discriminateur micro-ondes, etc.