Génie des micro-ondes - Mesures

Dans le domaine de l'ingénierie des micro-ondes, il existe de nombreuses applications, comme déjà indiqué dans le premier chapitre. Par conséquent, en utilisant différentes applications, nous rencontrons souvent le besoin de mesurer différentes valeurs telles que la puissance, l'atténuation, le déphasage, le VSWR, l'impédance, etc. pour une utilisation efficace.

Dans ce chapitre, examinons les différentes techniques de mesure.

Mesure de la puissance

La puissance micro-ondes mesurée est la puissance moyenne à n'importe quelle position dans le guide d'ondes. La mesure de puissance peut être de trois types.

• Mesure de faible puissance (0,01 mW à 10 mW)

  Exemple - Technique bolométrique

• Mesure de puissance moyenne (10 mW à 1 W)

  Exemple - Technique du calorimètre

• Mesure de haute puissance (> 10W)

  Exemple - Wattmètre calorimétrique

Examinons-les en détail.

Mesure de faible puissance

La mesure de la puissance micro-ondes autour de 0,01 mW à 10 mW, peut être comprise comme la mesure de faible puissance.

Bolometerest un appareil utilisé pour les mesures de faible puissance micro-ondes. L'élément utilisé dans le bolomètre peut être de coefficient de température positif ou négatif. Par exemple, un barrater a un coefficient de température positif dont la résistance augmente avec l'augmentation de la température. La thermistance a un coefficient de température négatif dont la résistance diminue avec l'augmentation de la température.

N'importe lequel d'entre eux peut être utilisé dans le bolomètre, mais le changement de résistance est proportionnel à la puissance micro-ondes appliquée pour la mesure. Ce bolomètre est utilisé dans un pont des bras comme un seul afin que tout déséquilibre causé, affecte la sortie. Un exemple typique de circuit en pont utilisant un bolomètre est illustré dans la figure suivante.

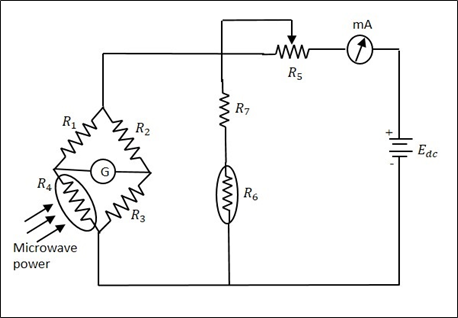
Le millimètre ici, donne la valeur du courant circulant. La batterie est variable, qui est variée pour obtenir l'équilibre, lorsqu'un déséquilibre est provoqué par le comportement du bolomètre. Cet ajustement qui est effectué en tension continue de la batterie est proportionnel à la puissance micro-ondes. La capacité de traitement de puissance de ce circuit est limitée.

Mesure de puissance moyenne

La mesure de la puissance micro-onde autour de 10mW à 1W, peut être comprise comme la mesure de puissance moyenne.

Une charge spéciale est utilisée, qui maintient généralement une certaine valeur de chaleur spécifique. La puissance à mesurer, est appliquée à son entrée qui change proportionnellement la température de sortie de la charge qu'elle maintient déjà. La différence d'élévation de température, spécifie la puissance micro-ondes d'entrée à la charge.

La technique d'équilibrage du pont est utilisée ici pour obtenir la sortie. La méthode de transfert de chaleur est utilisée pour la mesure de la puissance, qui est une technique calorimétrique.

Mesure de haute puissance

La mesure de la puissance micro-ondes autour de 10W à 50KW, peut être comprise comme la mesure d'une puissance élevée.

La puissance hyperfréquence élevée est normalement mesurée par des wattmètres calorimétriques, qui peuvent être de type sec et à débit. Le type sec est nommé ainsi car il utilise un câble coaxial qui est rempli de diélectrique à perte d'hystérésis élevée, tandis que le type d'écoulement est nommé ainsi car il utilise de l'eau ou de l'huile ou un liquide qui est un bon absorbeur de micro-ondes.

Le changement de température du liquide avant et après l'entrée de la charge, est pris pour l'étalonnage des valeurs. Les limites de cette méthode sont comme la détermination du débit, l'étalonnage et l'inertie thermique, etc.

Mesure de l'atténuation

En pratique, les composants et dispositifs micro-ondes fournissent souvent une certaine atténuation. La quantité d'atténuation offerte peut être mesurée de deux manières. Ce sont: la méthode du rapport de puissance et la méthode de substitution RF.

L'atténuation est le rapport entre la puissance d'entrée et la puissance de sortie et est normalement exprimée en décibels.

$$ Atténuation \: in \: dBs = 10 \: log \ frac {P_ {in}} {P_ {out}} $$

Où $ P_ {in} $ = puissance d'entrée et $ P_ {out} $ = puissance de sortie

Méthode du rapport de puissance

Dans cette méthode, la mesure de l'atténuation se fait en deux étapes.

• Step 1 - La puissance d'entrée et de sortie de l'ensemble du banc hyperfréquence se fait sans le dispositif dont l'atténuation doit être calculée.

• Step 2 - La puissance d'entrée et de sortie de l'ensemble du banc hyperfréquence se fait avec l'appareil dont l'atténuation doit être calculée.

Le rapport de ces puissances, comparé, donne la valeur de l'atténuation.

Les figures suivantes sont les deux configurations qui expliquent cela.

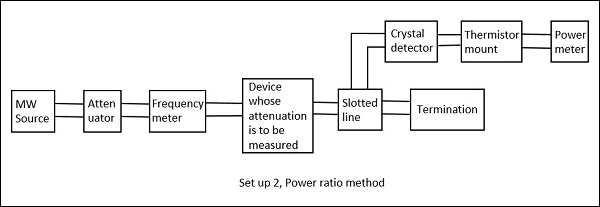
Drawback - Les mesures de puissance et d'atténuation peuvent ne pas être précises, lorsque la puissance d'entrée est faible et l'atténuation du réseau est importante.

Méthode de substitution RF

Dans cette méthode, la mesure de l'atténuation s'effectue en trois étapes.

• Step 1 - La puissance de sortie de l'ensemble du banc hyperfréquence est mesurée avec le réseau dont l'atténuation doit être calculée.

• Step 2 - La puissance de sortie de l'ensemble du banc hyperfréquence est mesurée en remplaçant le réseau par un atténuateur calibré de précision.

• Step 3 - Maintenant, cet atténuateur est réglé pour obtenir la même puissance que celle mesurée avec le réseau.

Les figures suivantes sont les deux configurations qui expliquent cela.

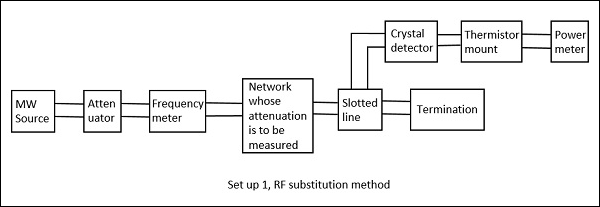
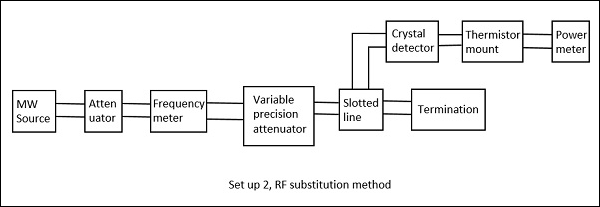
La valeur ajustée sur l'atténuateur donne directement l'atténuation du réseau. L'inconvénient de la méthode ci-dessus est évité ici et c'est donc une meilleure procédure pour mesurer l'atténuation.

Mesure du déphasage

Dans des conditions de travail pratiques, il peut se produire un changement de phase du signal à partir du signal réel. Pour mesurer un tel déphasage, nous utilisons une technique de comparaison, par laquelle nous pouvons calibrer le déphasage.

La configuration pour calculer le déphasage est illustrée dans la figure suivante.

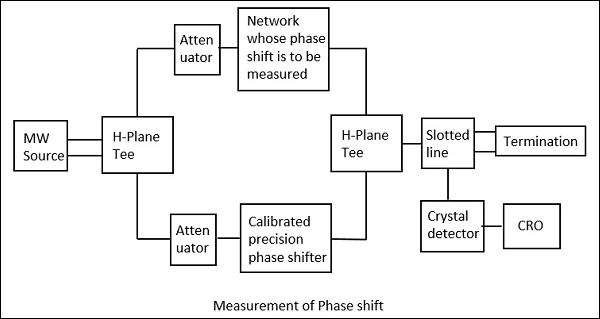
Ici, après que la source hyperfréquence a généré le signal, elle est passée à travers une jonction en T de plan H à partir de laquelle un port est connecté au réseau dont le déphasage doit être mesuré et l'autre port est connecté à un déphaseur de précision réglable.

La sortie démodulée est une onde sinusoïdale de 1 KHz, qui est observée dans le CRO connecté. Ce déphaseur est ajusté de telle sorte que sa sortie d'onde sinusoïdale de 1 KHz corresponde également à ce qui précède. Une fois l'appariement effectué en observant dans le CRO bi-mode, ce déphaseur de précision nous donne la lecture du déphasage. Ceci est clairement compris par la figure suivante.

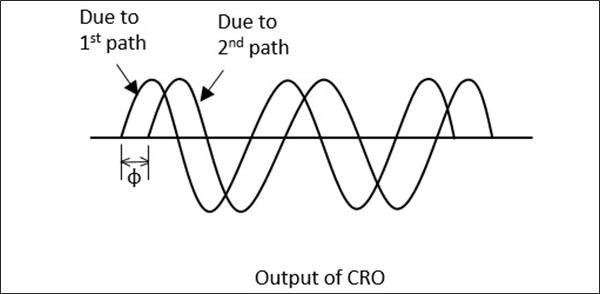
Cette procédure est la plus utilisée dans la mesure du déphasage. Voyons maintenant comment calculer le VSWR.

Mesure de VSWR

Dans toutes les applications pratiques des micro-ondes, tout type de désadaptation d'impédance conduit à la formation d'ondes stationnaires. La force de ces ondes stationnaires est mesurée par le rapport d'onde stationnaire de tension ($ VSWR $). Le rapport entre la tension maximale et la tension minimale donne le $ VSWR $, qui est noté $ S $.

$$ S = \ frac {V_ {max}} {V_ {min}} = \ frac {1+ \ rho} {1- \ rho} $$

Où, $ \ rho = reflet \: co - efficient = \ frac {P_ {reflété}} {P_ {incident}} $

La mesure de $ VSWR $ peut être effectuée de deux manières, les mesures Low $ VSWR $ et High $ VSWR $.

Mesure d'un VSWR faible (S <10)

La mesure d'un faible $ VSWR $ peut être effectuée en ajustant l'atténuateur pour obtenir une lecture sur un millivoltmètre CC qui est un compteur VSWR. Les lectures peuvent être prises en ajustant la ligne à fente et l'atténuateur de telle sorte que le millivoltmètre CC affiche une lecture pleine échelle ainsi qu'une lecture minimale.

Maintenant, ces deux lectures sont calculées pour connaître le $ VSWR $ du réseau.

Mesure d'un VSWR élevé (S> 10)

La mesure d'un $ VSWR $ élevé dont la valeur est supérieure à 10 peut être mesurée par une méthode appelée double minimum method. Dans cette méthode, la lecture à la valeur minimale est prise, et les lectures au demi-point de la valeur minimale dans la crête avant et la crête après sont également prises. Cela peut être compris par la figure suivante.

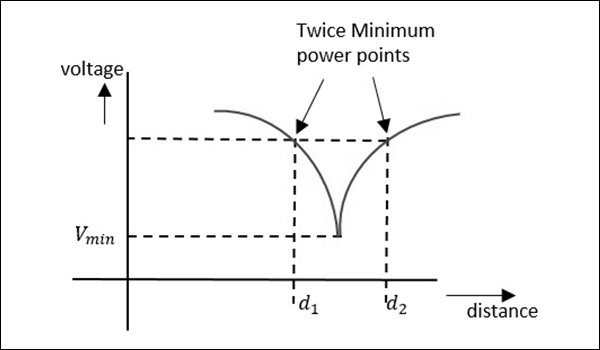
Maintenant, le $ VSWR $ peut être calculé par une relation, donnée comme -

$$ VSWR = \ frac {\ lambda_ {g}} {\ pi (d_2-d_1)} $$

Où, $ \ lambda_g \: est \: la \: guidée \: longueur d'onde $

$$ \ lambda_g = \ frac {\ lambda_0} {\ sqrt {1 - (\ frac {\ lambda_0} {\ lambda_c}) ^ 2}} \ quad où \: \ lambda_0 \: = {c} / {f} $$

Comme les deux points minimaux sont considérés ici, cela s'appelle la méthode du double minimum. Maintenant, apprenons la mesure de l'impédance.

Mesure d'impédance

Outre Magic Tee, nous avons deux méthodes différentes, l'une utilise la ligne à fente et l'autre utilise le réflectomètre.

Impédance en utilisant la ligne à fente

Dans cette méthode, l'impédance est mesurée en utilisant une ligne à fente et la charge $ Z_L $ et en utilisant cela, $ V_ {max} $ et $ V_ {min} $ peuvent être déterminés. Dans cette méthode, la mesure de l'impédance se fait en deux étapes.

• Step 1 - Détermination de Vmin à l'aide de load $ Z_L $.

• Step 2 - Détermination de Vmin en court-circuitant la charge.

Ceci est illustré dans les figures suivantes.

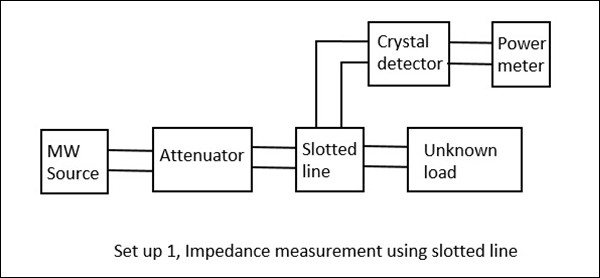
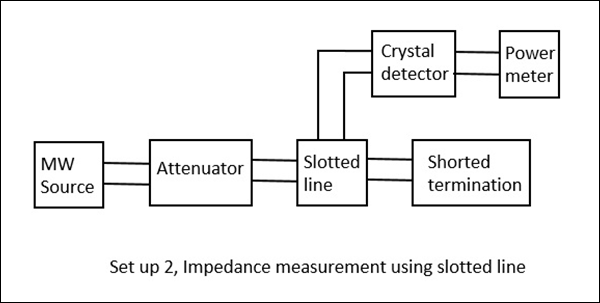
Lorsque nous essayons d'obtenir les valeurs de $ V_ {max} $ et $ V_ {min} $ en utilisant une charge, nous obtenons certaines valeurs. Cependant, si la même chose est faite en court-circuitant la charge, le minimum est décalé, soit vers la droite, soit vers la gauche. Si ce décalage est vers la gauche, cela signifie que la charge est inductive et si c'est le décalage vers la droite, cela signifie que la charge est de nature capacitive. La figure suivante explique cela.

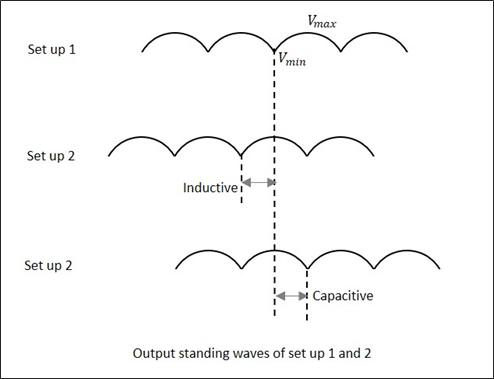
En enregistrant les données, une impédance inconnue est calculée. L'impédance et le coefficient de réflexion $ \ rho $ peuvent être obtenus à la fois en magnitude et en phase.

Impédance à l'aide du réflectomètre

Contrairement à la ligne à fentes, le réflectomètre aide à trouver uniquement l'amplitude de l'impédance et non l'angle de phase. Dans ce procédé, deux coupleurs directionnels identiques mais de direction différente sont pris.

Ces deux coupleurs sont utilisés pour échantillonner la puissance incidente $ P_i $ et la puissance réfléchie $ P_r $ de la charge. Le réflectomètre est connecté comme indiqué dans la figure suivante. Il est utilisé pour obtenir la grandeur du coefficient de réflexion $ \ rho $, à partir de laquelle l'impédance peut être obtenue.

À partir de la lecture du réflectomètre, nous avons

$$ \ rho = \ sqrt {\ frac {P_r} {P_i}} $$

A partir de la valeur de $ \ rho $, le $ VSWR $, c'est-à-dire $ S $ et l'impédance peuvent être calculés par

$$ S = \ frac {1+ \ rho} {1- \ rho} \ quad et \ quad \ frac {z-z_g} {z + z_g} = \ rho $$

Où, $ z_g $ est l'impédance d'onde connue et $ z $ est l'impédance inconnue.

Bien que les paramètres d'onde directe et inverse soient observés ici, il n'y aura pas d'interférence due à la propriété directionnelle des coupleurs. L'atténuateur aide à maintenir une faible puissance d'entrée.

Mesure du Q du résonateur de cavité

Bien qu'il existe trois méthodes telles que la méthode de transmission, la méthode d'impédance et la méthode de décroissance ou de décrémentation transitoire pour mesurer Q d'un résonateur à cavité, la méthode la plus simple et la plus suivie est la Transmission Method. Jetons donc un œil à sa configuration de mesure.

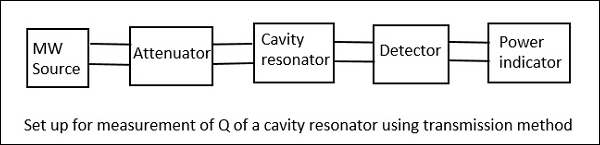
Dans cette méthode, le résonateur à cavité agit comme le dispositif qui transmet. Le signal de sortie est tracé en fonction de la fréquence, ce qui donne une courbe de résonance comme le montre la figure suivante.

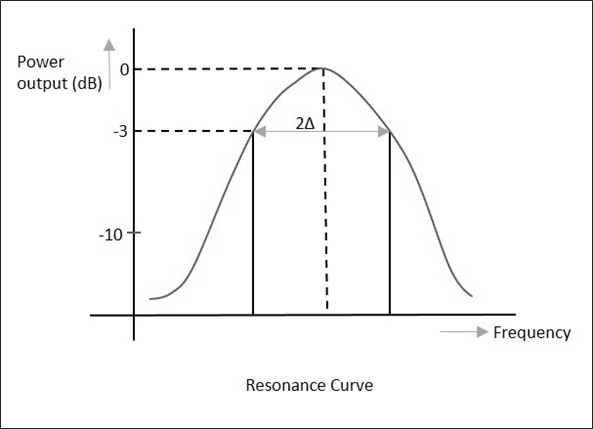
À partir de la configuration ci-dessus, la fréquence du signal de la source de micro-ondes est modifiée, en maintenant le niveau de signal constant, puis la puissance de sortie est mesurée. Le résonateur à cavité est accordé à cette fréquence, et le niveau du signal et la puissance de sortie sont à nouveau notés pour remarquer la différence.

Lorsque la sortie est tracée, la courbe de résonance est obtenue, à partir de laquelle nous pouvons remarquer les valeurs de Half Power Bandwidth (HPBW) $ (2 \ Delta) $.

$$ 2 \ Delta = \ pm \ frac {1} {Q_L} $$

Où, $ Q_L $ est la valeur chargée

$$ ou \ quad Q_L = \ pm \ frac {1} {2 \ Delta} = \ pm \ frac {w} {2 (w-w_0)} $$

Si le couplage entre la source hyperfréquence et la cavité, ainsi que le couplage entre le détecteur et la cavité sont négligés, alors

$$ Q_L = Q_0 \: (déchargé \: Q) $$

Inconvénient

Le principal inconvénient de ce système est que la précision est un peu médiocre dans les systèmes à Q très élevé en raison d'une bande de fonctionnement étroite.

Nous avons couvert de nombreux types de techniques de mesure de différents paramètres. Maintenant, essayons de résoudre quelques exemples de problèmes sur ces derniers.