Génie micro-ondes - Appareils micro-ondes

Tout comme les autres systèmes, les systèmes hyperfréquences se composent de nombreux composants hyperfréquences, principalement avec une source à une extrémité et une charge à l'autre, qui sont tous connectés à des guides d'ondes ou à des systèmes de câbles coaxiaux ou de lignes de transmission.

Voici les propriétés des guides d'ondes.

SNR élevé
Faible atténuation
Moins de perte d'insertion

Fonctions micro-ondes du guide d'ondes

Considérez un guide d'ondes ayant 4 ports. Si l'alimentation est appliquée à un port, elle passe par les 3 ports dans certaines proportions où une partie peut se refléter du même port. Ce concept est clairement illustré dans la figure suivante.

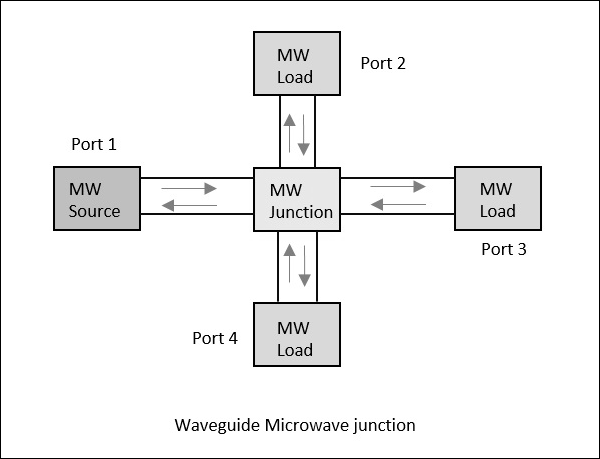
Paramètres de diffusion

Pour un réseau à deux ports, comme le montre la figure suivante, si l'alimentation est appliquée à un port, comme nous venons de le voir, la plupart de l'alimentation s'échappe de l'autre port, tandis qu'une partie est renvoyée vers le même port. Dans la figure suivante, siV₁ ou V₂ est appliqué, alors I₁ ou I₂ le courant circule respectivement.

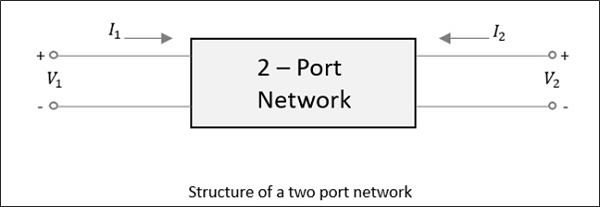
Si la source est appliquée au port opposé, deux autres combinaisons doivent être envisagées. Ainsi, pour un réseau à deux ports, 2 × 2 = 4 combinaisons sont susceptibles de se produire.

Les ondes progressives avec les puissances associées lorsqu'elles se dispersent dans les ports, la jonction hyperfréquence peut être définie par des paramètres Scattering Parameters, qui sont représentés sous une forme matricielle, appelée "Scattering Matrix".

Matrice de dispersion

C'est une matrice carrée qui donne toutes les combinaisons de relations de puissance entre les différents ports d'entrée et de sortie d'une jonction hyperfréquence. Les éléments de cette matrice sont appelés"Scattering Coefficients" ou "Scattering (S) Parameters".

Considérez la figure suivante.

Ici, la source est connectée via la ligne $ i ^ {th} $ tandis que $ a_1 $ est l'onde incidente et $ b_1 $ est l'onde réfléchie.

Si une relation est donnée entre $ b_1 $ et $ a_1 $,

$$ b_1 = (réflexion \: \: coefficient) a_1 = S_ {1i} a_1 $$

Où

$ S_ {1i} $ = coefficient de réflexion de $ 1 ^ {st} $ line (où $ i $ est le port d'entrée et $ 1 $ est le port de sortie)
$ 1 $ = Réflexion de la ligne $ 1 ^ {st} $
$ i $ = Source connectée à la ligne $ i ^ {th} $

Si l'impédance correspond, alors la puissance est transférée à la charge. Peu probable, si l'impédance de charge ne correspond pas à l'impédance caractéristique. Ensuite, la réflexion se produit. Cela signifie que la réflexion se produit si

$$ Z_l \ neq Z_o $$

Cependant, si cette discordance existe pour plus d'un port, par exemple $ 'n' $ ports, alors $ i = 1 $ à $ n $ (puisque $ i $ peut être n'importe quelle ligne de $ 1 $ à $ n $).

Par conséquent, nous avons

$$ b_1 = S_ {11} a_1 + S_ {12} a_2 + S_ {13} a_3 + ............... + S_ {1n} a_n $$

$$ b_2 = S_ {21} a_1 + S_ {22} a_2 + S_ {23} a_3 + ............... + S_ {2n} a_n $$

$$. $$

$$ b_n = S_ {n1} a_1 + S_ {n2} a_2 + S_ {n3} a_3 + ............... + S_ {nn} a_n $$

Lorsque tout cela est conservé sous forme de matrice,

$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \\. \\. \\. \\ b_n \ end {bmatrix} = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13 } & ... & S_ {1n} \\ S_ {21} & S_ {22} & S_ {23} & ... & S_ {2n} \\. &. &. & ... &. \\. &. &. & ... &. \\. &. &. & ... &. \\ S_ {n1} & S_ {n2} & S_ {n3} & ... & S_ {nn} \\ \ end {bmatrix} \ times \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \\. \ \. \\. \\ a_n \ end {bmatrix} $$

Column matrix $ [b] $ Scattering matrix $ [S] $Matrix $ [a] $

La matrice colonne $ \ left [b \ right] $ correspond aux ondes réfléchies ou à la sortie, tandis que la matrice $ \ left [a \ right] $ correspond aux ondes incidentes ou à l'entrée. La matrice de colonnes de diffusion $ \ left [s \ right] $ qui est de l'ordre de $ n \ fois n $ contient les coefficients de réflexion et de transmission. Par conséquent,

$$ \ left [b \ right] = \ left [S \ right] \ left [a \ right] $$

Propriétés de [S] Matrix

La matrice de diffusion est indiquée par $ [S] $ matrix. Il existe peu de propriétés standard pour la matrice $ [S] $. Ils sont -

$ [S] $ est toujours une matrice carrée d'ordre (nxn)

$ [S] _ {n \ fois n} $
$ [S] $ est une matrice symétrique

c'est-à-dire $ S_ {ij} = S_ {ji} $
$ [S] $ est une matrice unitaire

c'est-à-dire $ [S] [S] ^ * = I $
La somme des produits de chaque terme de toute ligne ou colonne multipliée par le conjugué complexe des termes correspondants de toute autre ligne ou colonne est égale à zéro. c'est à dire,

$$ \ sum_ {i = j} ^ {n} S_ {ik} S_ {ik} ^ {*} = 0 \: pour \: k \ neq j $$

$$ (k = 1,2,3, ... \: n) \: et \: (j = 1,2,3, ... \: n) $$

Si la distance électrique entre un port $ k ^ {th} $ et la jonction est $ \ beta _kI_k $, alors les coefficients de $ S_ {ij} $ impliquant $ k $, seront multipliés par le facteur $ e ^ {- j \ beta kIk} $

Dans les prochains chapitres, nous examinerons différents types de jonctions micro-ondes en T.