Ingénierie des micro-ondes - Guide rapide
Le spectre électromagnétique se compose d'une gamme complète de rayonnement électromagnétique. Le rayonnement est l'énergie qui se déplace et se répand à mesure qu'elle se propage. Les types de rayonnement électromagnétique qui composent le spectre électromagnétique sont illustrés dans la capture d'écran suivante.
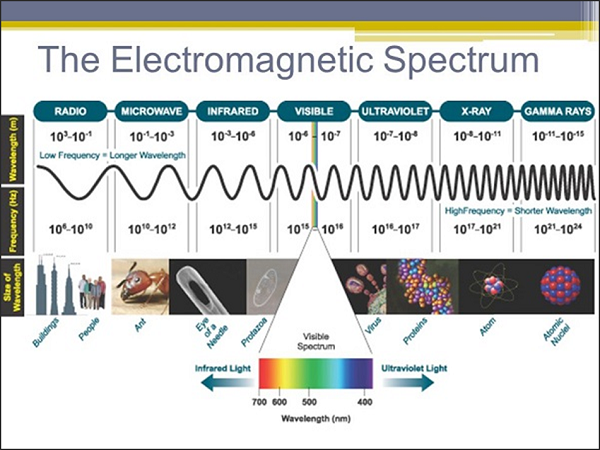
Jetons maintenant un œil aux propriétés des micro-ondes.
Propriétés des micro-ondes
Voici les principales propriétés des micro-ondes.
Les micro-ondes sont les ondes qui rayonnent de l'énergie électromagnétique avec une longueur d'onde plus courte.
Les micro-ondes ne sont pas réfléchies par l'ionosphère.
Les micro-ondes voyagent en ligne droite et sont réfléchies par les surfaces conductrices.
Les micro-ondes sont facilement atténués sur des distances plus courtes.
Les courants micro-ondes peuvent circuler à travers une fine couche d'un câble.
Avantages des micro-ondes
Les micro-ondes présentent de nombreux avantages tels que les suivants:
Prend en charge une bande passante plus grande et donc plus d'informations sont transmises. Pour cette raison, les micro-ondes sont utilisées pour les communications point à point.
Plus de gain d'antenne est possible.
Des débits de données plus élevés sont transmis à mesure que la bande passante augmente.
La taille de l'antenne est réduite, car les fréquences sont plus élevées.
Faible consommation d'énergie car les signaux sont de fréquences plus élevées.
L'effet de l'évanouissement est réduit en utilisant la propagation en ligne de visée.
Fournit une zone de réflexion efficace dans les systèmes radar.
Des communications satellitaires et terrestres à haute capacité sont possibles.
Des composants micro-ondes miniatures peu coûteux peuvent être développés.
Utilisation efficace du spectre avec une grande variété d'applications dans toutes les plages de fréquences de fonctionnement disponibles.
Inconvénients des micro-ondes
Il y a quelques inconvénients des micro-ondes tels que les suivants -
- Le coût de l'équipement ou le coût d'installation est élevé.
- Ils sont lourds et occupent plus d'espace.
- Des interférences électromagnétiques peuvent se produire.
- Des variations des propriétés diélectriques avec les températures peuvent se produire.
- Inefficacité inhérente de l'énergie électrique.
Applications des micro-ondes
Il existe une grande variété d'applications pour les micro-ondes, qui ne sont pas possibles pour d'autres rayonnements. Ils sont -
Communications sans fil
- Pour les appels téléphoniques longue distance
- Bluetooth
- Opérations WIMAX
- Émissions de diffusion extérieure
- Services auxiliaires de diffusion
- Unité de ramassage à distance
- Lien studio / émetteur
- Satellite de diffusion directe (DBS)
- Systèmes de communication personnels (PCS)
- Réseaux locaux sans fil (WLAN)
- Systèmes de vidéo cellulaire (CV)
- Système d'évitement de collision automobile
Électronique
- Commutateurs rapides sans gigue
- Déphaseurs
- Génération HF
- Éléments de réglage
- Systèmes ECM / ECCM (contre-mesure électronique)
- Systèmes à spectre étalé
Utilisations commerciales
- Alarmes antivol
- Ouvre-portes de garage
- Détecteurs de vitesse de la police
- Identification par des méthodes sans contact
- Téléphones portables, téléavertisseurs, réseaux locaux sans fil
- Télévision par satellite, radio XM
- Détecteurs de mouvement
- Télédétection
La navigation
- Systèmes mondiaux de navigation par satellite
- Système de positionnement global (GPS)
Militaire et radar
Radars pour détecter la portée et la vitesse de la cible.
Applications SONAR
Le contrôle du trafic aérien
Prévision météo
Navigation des navires
Applications de déminage
Application des limites de vitesse
L'armée utilise des fréquences micro-ondes pour les communications et pour les applications mentionnées ci-dessus.
Applications de recherche
- Résonances atomiques
- Résonances nucléaires
Radioastronomie
- Marquer le rayonnement de fond des micro-ondes cosmiques
- Détection de puissantes vagues dans l'univers
- Détection de nombreux rayonnements dans l'univers et l'atmosphère terrestre
Industrie alimentaire
- Fours à micro-ondes utilisés pour le réchauffage et la cuisson
- Applications de transformation des aliments
- Applications de préchauffage
- Pre-cooking
- Torréfaction de céréales / haricots
- Séchage de croustilles
- Nivellement d'humidité
- Absorber les molécules d'eau
Utilisations industrielles
- Caoutchouc vulcanisant
- Applications de chimie analytique
- Processus de séchage et de réaction
- Traitement de la céramique
- Matrice polymère
- Modification de surface
- Traitement chimique des vapeurs
- Traitement de la poudre
- Produits pharmaceutiques stérilisants
- Synthèse chimique
- Assainissement des déchets
- Puissance de transmission
- Forage de tunnel
- Briser la roche / le béton
- Briser les veines de charbon
- Durcissement du ciment
- Éclairage RF
- Réacteurs à fusion
- Systèmes de déni actifs
Techniques de traitement des semi-conducteurs
- Gravure ionique réactive
- Dépôt chimique en phase vapeur
Spectroscopie
- Spectroscopie par résonance paramagnétique électronique (EPR ou ESR)
- Connaître les électrons non appariés dans les produits chimiques
- Connaître les radicaux libres dans les matériaux
- Chimie électronique
Applications médicales
- Surveillance du rythme cardiaque
- Détection d'eau pulmonaire
- Détection des tumeurs
- Hyperthermie régionale
- Applications thérapeutiques
- Chauffage local
- Angioplasty
- Tomographie par micro-ondes
- Imagerie acoustique micro-ondes
Pour qu'une vague se propage, il faut un médium. Les lignes de transmission, de types différents, sont utilisées pour la propagation des micro-ondes. Découvrons-les dans le prochain chapitre.
UNE transmission lineest un connecteur qui transmet l'énergie d'un point à un autre. L'étude de la théorie des lignes de transmission est utile dans l'utilisation efficace de l'énergie et de l'équipement.
Il existe essentiellement quatre types de lignes de transmission -
- Lignes de transmission parallèles à deux fils
- Lignes coaxiales
- Lignes de transmission de substrat de type bande
- Waveguides
Lors de la transmission ou de la réception, le transfert d'énergie doit être effectué efficacement, sans gaspillage d'énergie. Pour y parvenir, certains paramètres importants doivent être pris en compte.
Paramètres principaux d'une ligne de transport
Les paramètres importants d'une ligne de transmission sont la résistance, l'inductance, la capacité et la conductance.
La résistance et l'inductance ensemble sont appelées comme ligne de transmission impedance.
La capacité et la conductance ensemble sont appelées comme admittance.
La résistance
La résistance offerte par le matériau dont sont constituées les lignes de transmission sera considérable, en particulier pour les lignes plus courtes. À mesure que le courant de ligne augmente, la perte ohmique $ \ left (I ^ {2} R \: loss \ right) $ augmente également.
La résistance $R$ d'un conducteur de longueur "$l$" et coupe transversale "$a$" est représenté par
$$ R = \ rho \ frac {l} {a} $$
Où
?? $ \ rho $ = résistivité du matériau conducteur, qui est constante.
La température et la fréquence du courant sont les principaux facteurs qui affectent la résistance d'une ligne. La résistance d'un conducteur varie linéairement avec le changement de température. Alors que si la fréquence du courant augmente, la densité de courant vers la surface du conducteur augmente également. Sinon, la densité de courant vers le centre du conducteur augmente.
Cela signifie que plus le courant circule vers la surface du conducteur, moins il s'écoule vers le centre, ce que l'on appelle le Skin Effect.
Inductance
Dans une ligne de transmission CA, le courant circule de manière sinusoïdale. Ce courant induit un champ magnétique perpendiculaire au champ électrique, qui varie également de manière sinusoïdale. C'est bien connu comme la loi de Faraday. Les champs sont représentés dans la figure suivante.

Ce champ magnétique variable induit une certaine EMF dans le conducteur. Maintenant, cette tension induite ou EMF circule dans le sens opposé au courant circulant initialement. Cette CEM circulant dans la direction opposée est représentée de manière équivalente par un paramètre connu sous le nom deInductance, qui est la propriété de s'opposer au décalage dans le courant.
Il est indiqué par "L". L'unité de mesure est"Henry(H)".
Conductance
Il y aura un courant de fuite entre la ligne de transmission et la terre, ainsi qu'entre les conducteurs de phase. Cette petite quantité de courant de fuite circule généralement à travers la surface de l'isolant. L'inverse de ce courant de fuite est appeléConductance. Il est indiqué par "G".
Le flux de courant de ligne est associé à l'inductance et la différence de tension entre les deux points est associée à la capacité. L'inductance est associée au champ magnétique, tandis que la capacité est associée au champ électrique.
Capacitance
La différence de tension entre le Phase conductorsdonne lieu à un champ électrique entre les conducteurs. Les deux conducteurs sont comme des plaques parallèles et l'air entre eux devient diélectrique. Ce motif donne lieu à l'effet de capacité entre les conducteurs.
Impédance caractéristique
Si une ligne de transmission uniforme sans perte est considérée, pour une onde voyageant dans une direction, le rapport des amplitudes de tension et de courant le long de cette ligne, qui n'a pas de réflexions, est appelé Characteristic impedance.
Il est noté $ Z_0 $
$$ Z_0 = \ sqrt {\ frac {voltage \: \: wave \: \: value} {current \: \: wave \: \: value}} $$
$$ Z_0 = \ sqrt {\ frac {R + jwL} {G + jwC}} $$
Pour une ligne sans perte, $ R_0 = \ sqrt {\ frac {L} {C}} $
Où $ L $ et $ C $ sont l'inductance et la capacité par unité de longueur.
Adaptation d'impédance
Pour obtenir un transfert de puissance maximal vers la charge, une adaptation d'impédance doit être effectuée. Pour réaliser cette adaptation d'impédance, les conditions suivantes doivent être remplies.
La résistance de la charge doit être égale à celle de la source.
$$ R_L = R_S $$
La réactance de la charge doit être égale à celle de la source mais de signe opposé.
$$ X_L = -X_S $$
Ce qui signifie que si la source est inductive, la charge doit être capacitive et vice versa.
Coefficient de reflexion
Le paramètre qui exprime la quantité d'énergie réfléchie due à une discordance d'impédance dans une ligne de transmission est appelé Reflection coefficient. Il est indiqué par $ \ rho $(rho).
Il peut être défini comme "le rapport entre la tension réfléchie et la tension incidente aux bornes de la charge".
$$ \ rho = \ frac {reflété \: voltage} {incident \: voltage} = \ frac {V_r} {V_i} \: at \: load \: terminaux $$
Si l'impédance entre l'appareil et la ligne de transmission ne correspond pas, l'énergie est réfléchie. Plus l'énergie réfléchie est élevée, plus la valeur du coefficient de réflexion $ \ rho $ sera élevée.
Rapport d'onde stationnaire de tension (VSWR)
L'onde stationnaire se forme lorsque l'onde incidente est réfléchie. L'onde stationnaire qui se forme contient une certaine tension. L'amplitude des ondes stationnaires peut être mesurée en termes de rapports d'ondes stationnaires.
Le rapport entre la tension maximale et la tension minimale dans une onde stationnaire peut être défini comme le rapport d'onde stationnaire de tension (VSWR). Il est noté "$ S $".
$$ S = \ frac {\ left | V_ {max} \ right |} {\ left | V_ {min} \ right |} \ quad 1 \: \ leq S \ leq \ infty $$
VSWR décrit le modèle d'onde stationnaire de tension qui est présent dans la ligne de transmission en raison de l'addition et de la soustraction de phase des ondes incidentes et réfléchies.
Par conséquent, il peut également être écrit comme
$$ S = \ frac {1 + \ rho} {1 - \ rho} $$
Plus la discordance d'impédance est grande, plus l'amplitude de l'onde stationnaire sera élevée. Par conséquent, si l'impédance est parfaitement adaptée,
$$ V_ {max}: V_ {min} = 1: 1 $$
Par conséquent, la valeur de VSWR est l'unité, ce qui signifie que la transmission est parfaite.
Efficacité des lignes de transport
L'efficacité des lignes de transmission est définie comme le rapport entre la puissance de sortie et la puissance d'entrée.
$ \% \: efficacité \: of \: transmission \: line \: \ eta = \ frac {Puissance \: livrée \: à \: réception} {Puissance \: envoyée \: de \: la \: transmission \: fin} \ fois 100 $
Régulation de tension
La régulation de tension est définie comme le changement de l'amplitude de la tension entre les extrémités d'émission et de réception de la ligne de transmission.
$ \% \: voltage \: regulation = \ frac {envoi \: end \: voltage - \: reception \: end \: voltage} {envoi \: end \: voltage} \ times 100 $
Pertes dues à une discordance d'impédance
La ligne de transmission, si elle n'est pas terminée par une charge adaptée, se produit en pertes. Ces pertes sont de nombreux types tels que la perte d'atténuation, la perte de réflexion, la perte de transmission, la perte de retour, la perte d'insertion, etc.
Atténuation Perte
La perte qui se produit en raison de l'absorption du signal dans la ligne de transmission est appelée perte d'atténuation, qui est représentée par
$$ Atténuation \: loss (dB) = 10 \: log_ {10} \ left [\ frac {E_i - E_r} {E_t} \ right] $$
Où
$ E_i $ = l'énergie d'entrée
$ E_r $ = l'énergie réfléchie de la charge vers l'entrée
$ E_t $ = l'énergie transmise à la charge
Perte de réflexion
La perte qui se produit en raison de la réflexion du signal due à une discordance d'impédance de la ligne de transmission est appelée perte de réflexion, qui est représentée par
$$ Réflexion \: loss (dB) = 10 \: log_ {10} \ left [\ frac {E_i} {E_i - E_r} \ right] $$
Où
$ E_i $ = l'énergie d'entrée
$ E_r $ = l'énergie réfléchie par la charge
Perte de transmission
La perte qui se produit lors de la transmission via la ligne de transmission est appelée perte de transmission, représentée par
$$ Transmission \: loss (dB) = 10 \: log_ {10} \: \ frac {E_i} {E_t} $$
Où
$ E_i $ = l'énergie d'entrée
$ E_t $ = l'énergie transmise
Perte de retour
La mesure de la puissance réfléchie par la ligne de transmission est appelée perte de retour, qui est représentée par
$$ Return \: loss (dB) = 10 \: log_ {10} \: \ frac {E_i} {E_r} $$
Où
$ E_i $ = l'énergie d'entrée
$ E_r $ = l'énergie réfléchie
Perte d'insertion
La perte qui se produit en raison du transfert d'énergie utilisant une ligne de transmission par rapport au transfert d'énergie sans ligne de transmission est appelée perte d'insertion, qui est représentée par
$$ Insertion \: loss (dB) = 10 \: log_ {10} \: \ frac {E_1} {E_2} $$
Où
$ E_1 $ = l'énergie reçue par la charge lorsqu'elle est directement connectée à la source, sans ligne de transmission.
$ E_2 $ = l'énergie reçue par la charge lorsque la ligne de transmission est connectée entre la charge et la source.
Correspondance de stub
Si l'impédance de charge ne correspond pas à l'impédance source, une méthode appelée "Stub Matching" est parfois utilisée pour réaliser la correspondance.
Le processus de connexion des sections de lignes ouvertes ou en court-circuit appelé stubs dans le shunt avec la ligne principale à un ou plusieurs points, peut être appelé Stub Matching.
À des fréquences micro-ondes plus élevées, deux techniques de correspondance de stub sont essentiellement utilisées.
Correspondance de stub unique
Dans l'appariement de stub simple, un talon d'une certaine longueur fixe est placé à une certaine distance de la charge. Il n'est utilisé que pour une fréquence fixe, car pour tout changement de fréquence, l'emplacement du stub doit être changé, ce qui n'est pas fait. Cette méthode ne convient pas aux lignes coaxiales.
Correspondance double stub
Dans l'appariement à deux montants, deux talons de longueur variable sont fixés à certaines positions. Au fur et à mesure que la charge change, seules les longueurs des stubs sont ajustées pour obtenir la correspondance. Ceci est largement utilisé dans la pratique de laboratoire comme dispositif d'adaptation de fréquence unique.
Les figures suivantes montrent à quoi ressemblent les correspondances de stub.
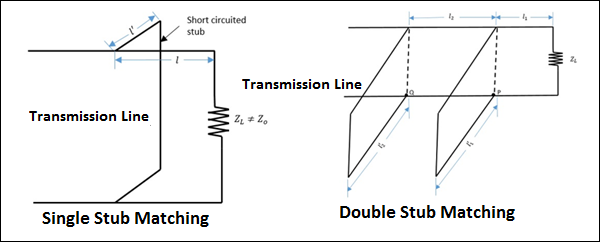
L'adaptation de tronçon simple et l'adaptation de tronçon double, comme le montrent les figures ci-dessus, sont effectuées dans les lignes de transmission pour obtenir une adaptation d'impédance.
Une onde a à la fois des champs électriques et magnétiques. Toutes les composantes transversales des champs électriques et magnétiques sont déterminées à partir des composantes axiales du champ électrique et magnétique, dans la direction z. Cela permet des formations de mode, telles que TE, TM, TEM et Hybrid dans les micro-ondes. Jetons un coup d'œil aux types de modes.
La direction des composantes du champ électrique et magnétique le long de trois directions perpendiculaires l'une à l'autre x, y et z est indiquée sur la figure suivante.

Types de modes
Les modes de propagation des micro-ondes sont -
TEM (onde électromagnétique transversale)
Dans ce mode, les champs électriques et magnétiques sont à la fois purement transversaux à la direction de propagation. Il n'y a pas de composants dans la direction $ 'Z' $.
$$ E_z = 0 \: et \: H_z = 0 $$
TE (onde électrique transversale)
Dans ce mode, le champ électrique est purement transversal à la direction de propagation, alors que le champ magnétique ne l'est pas.
$$ E_z = 0 \: et \: H_z \ ne 0 $$
TM (onde magnétique transversale)
Dans ce mode, le champ magnétique est purement transversal à la direction de propagation, alors que le champ électrique ne l'est pas.
$$ E_z \ ne 0 \: et \: H_z = 0 $$
HE (vague hybride)
Dans ce mode, ni le champ électrique ni le champ magnétique ne sont purement transversaux à la direction de propagation.
$$ E_z \ ne 0 \: et \: H_z \ ne 0 $$
Les lignes multiconductrices prennent normalement en charge le mode de propagation TEM, car la théorie des lignes de transmission est applicable uniquement aux systèmes de conducteurs qui ont un chemin aller et retour, c'est-à-dire ceux qui peuvent supporter une onde TEM.
Les guides d'ondes sont des lignes à conducteur unique qui autorisent les modes TE et TM mais pas le mode TEM. Les guides conducteurs ouverts prennent en charge les ondes hybrides. Les types de lignes de transmission sont discutés dans le chapitre suivant.
Les lignes de transmission à fil ouvert conventionnelles ne conviennent pas à la transmission hyperfréquence, car les pertes de rayonnement seraient élevées. Aux fréquences hyperfréquences, les lignes de transmission employées peuvent être globalement classées en trois types. Ils sont -
- Lignes multi-conducteurs
- Lignes coaxiales
- Lignes de bande
- Lignes de micro-bandes
- Lignes de fente
- Lignes coplanaires, etc.
- Lignes à conducteur unique (guides d'ondes)
- Guides d'ondes rectangulaires
- Guides d'ondes circulaires
- Guides d'ondes elliptiques
- Guides d'ondes à simple arête
- Guides d'ondes à double arête, etc.
- Structures de frontières ouvertes
- Tiges diélectriques
- Guides d'ondes ouverts, etc.
Lignes multiconducteurs
Les lignes de transmission qui ont plus d'un conducteur sont appelées lignes multiconductrices.
Lignes coaxiales
Celui-ci est principalement utilisé pour les applications haute fréquence.
Une ligne coaxiale se compose d'un conducteur intérieur de diamètre intérieur d, puis un matériau isolant cylindrique concentrique, autour de lui. Celui-ci est entouré d'un conducteur extérieur, qui est un cylindre concentrique avec un diamètre intérieurD. Cette structure est bien comprise en regardant la figure suivante.
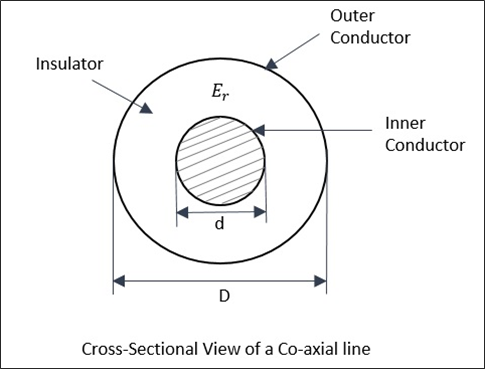
Le mode fondamental et dominant dans les câbles coaxiaux est le mode TEM. Il n'y a pas de fréquence de coupure dans le câble coaxial. Il passe toutes les fréquences. Cependant, pour les fréquences plus élevées, certains modes non-TEM d'ordre supérieur commencent à se propager, provoquant une forte atténuation.
Lignes de bande
Ce sont les lignes de transmission planes, utilisées à des fréquences de 100 MHz à 100 GHz.
UNE Strip line se compose d'une fine bande conductrice centrale de largeur ω qui est supérieure à son épaisseur t. Il est placé à l'intérieur du substrat diélectrique à faibles pertes (ε r ) d'épaisseur b / 2 entre deux larges plaques de masse. La largeur des plaques de sol est cinq fois supérieure à l'espacement entre les plaques.
L'épaisseur du conducteur central métallique et l'épaisseur des plans de masse métalliques sont les mêmes. La figure suivante montre la vue en coupe de la structure de ligne de bande.
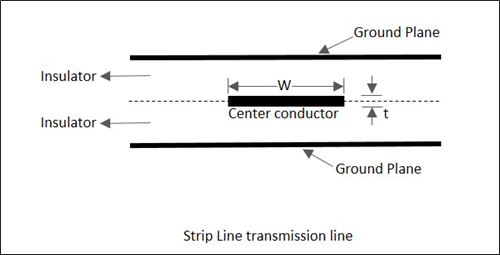
Le mode fondamental et dominant dans les lignes Strip est le mode TEM. Pourb<λ/2, il n'y aura pas de propagation dans le sens transversal. L'impédance d'une ligne en bande est inversement proportionnelle au rapport de la largeurω du conducteur intérieur à la distance b entre les plans au sol.
Lignes Micro Strip
La ligne de bande a pour inconvénient de ne pas être accessible pour le réglage et le réglage. Ceci est évité dans les lignes à micro-bandes, ce qui permet le montage de dispositifs actifs ou passifs, et permet également d'effectuer des ajustements mineurs après la fabrication du circuit.
Une ligne de micro-bandes est une ligne de transmission à plaques parallèles asymétriques, ayant un substrat diélectrique qui a un sol métallisé sur le fond et une mince bande conductrice sur le dessus avec une épaisseur.t'et largeur'ω». Ceci peut être compris en regardant la figure suivante, qui montre une ligne de micro-bandes.
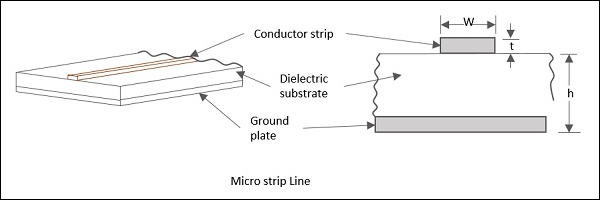
L'impédance caractéristique d'une micro bande est fonction de la largeur de la ligne de bande (ω), épaisseur (t) et la distance entre la ligne et le plan du sol (h). Les lignes de micro-bandes sont de nombreux types tels que les micro-bandes intégrées, les micro-bandes inversées, les micro-bandes suspendues et les lignes de transmission à micro-bandes à fentes.
En plus de celles-ci, certaines autres lignes TEM telles que des lignes à bandes parallèles et des lignes à bandes coplanaires ont également été utilisées pour des circuits intégrés hyperfréquences.
Autres lignes
UNE Parallel Strip lineest similaire à une ligne de transmission à deux conducteurs. Il peut prendre en charge le mode quasi TEM. La figure suivante explique cela.

UNE Coplanar strip lineest formé de deux bandes conductrices avec une bande mise à la terre, toutes deux placées sur la même surface de substrat, pour des connexions pratiques. La figure suivante explique cela.
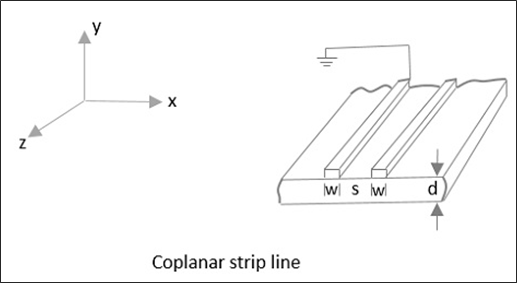
UNE Slot line transmission line, consiste en une fente ou un espace dans un revêtement conducteur sur un substrat diélectrique et ce procédé de fabrication est identique aux lignes de micro-bandes. Voici sa représentation schématique.
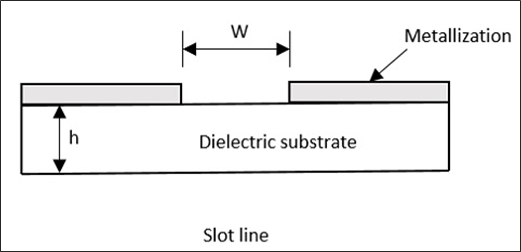
Un guide d'ondes coplanaire est constitué d'une bande de film métallique mince qui est déposée sur la surface d'une plaque diélectrique. Cette dalle comporte deux électrodes adjacentes et parallèles à la bande sur la même surface. La figure suivante explique cela.
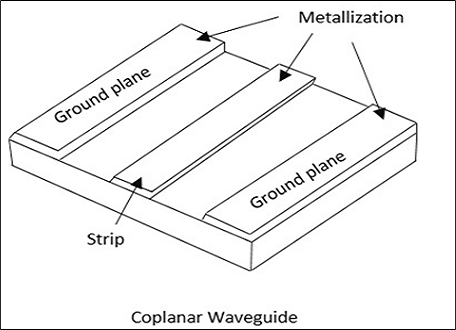
Toutes ces lignes de micro-bandes sont utilisées dans des applications micro-ondes où l'utilisation de lignes de transmission encombrantes et coûteuses à fabriquer sera un inconvénient.
Structures aux limites ouvertes
Ceux-ci peuvent également être indiqués comme Open Electromagnetic Waveguides. Un guide d'ondes qui n'est pas entièrement enfermé dans un blindage métallique peut être considéré comme un guide d'ondes ouvert. L'espace libre est également considéré comme une sorte de guide d'ondes ouvert.
Un guide d'ondes ouvert peut être défini comme tout dispositif physique à symétrie axiale longitudinale et à section transversale illimitée, capable de guider des ondes électromagnétiques. Ils possèdent un spectre qui n'est plus discret. Les micro-bandes et les fibres optiques sont également des exemples de guides d'ondes ouverts.
En général, si la fréquence d'un signal ou d'une bande de signaux particulière est élevée, l'utilisation de la bande passante est élevée car le signal offre plus d'espace pour que d'autres signaux s'accumulent. Cependant, les signaux haute fréquence ne peuvent pas parcourir de plus longues distances sans être atténués. Nous avons étudié que les lignes de transmission aident les signaux à parcourir de plus longues distances.
Les micro-ondes se propagent à travers des circuits, des composants et des dispositifs micro-ondes, qui agissent comme une partie des lignes de transmission micro-ondes, généralement appelées guides d'ondes.
Un tube métallique creux de section transversale uniforme pour transmettre des ondes électromagnétiques par réflexions successives des parois internes du tube est appelé comme un Waveguide.
La figure suivante montre un exemple de guide d'ondes.
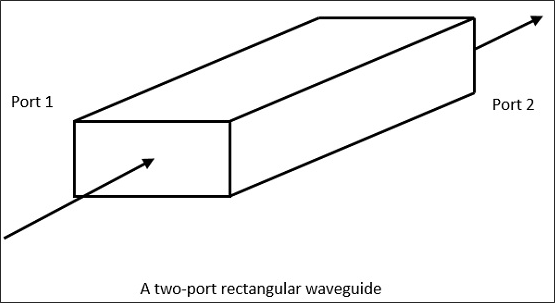
Un guide d'ondes est généralement préféré dans les communications micro-ondes. Le guide d'ondes est une forme spéciale de ligne de transmission, qui est un tube métallique creux. Contrairement à une ligne de transmission, un guide d'ondes n'a pas de conducteur central.
Les principales caractéristiques d'un guide d'ondes sont:
La paroi du tube fournit une inductance distribuée.
L'espace vide entre les parois du tube fournit une capacité distribuée.
Ceux-ci sont encombrants et coûteux.
Avantages des guides d'ondes
Voici quelques avantages des guides d'ondes.
Les guides d'ondes sont faciles à fabriquer.
Ils peuvent supporter une très grande puissance (en kilo watts).
La perte de puissance est très négligeable dans les guides d'ondes.
Ils offrent une très faible perte (faible valeur de l'atténuation alpha).
Lorsque l'énergie micro-ondes se propage à travers le guide d'ondes, elle subit des pertes plus faibles qu'un câble coaxial.
Types de guides d'ondes
Il existe cinq types de guides d'ondes.
- Guide d'ondes rectangulaire
- Guide d'ondes circulaire
- Guide d'ondes elliptique
- Guide d'ondes à simple arête
- Guide d'ondes à double arête
Les figures suivantes montrent les types de guides d'ondes.
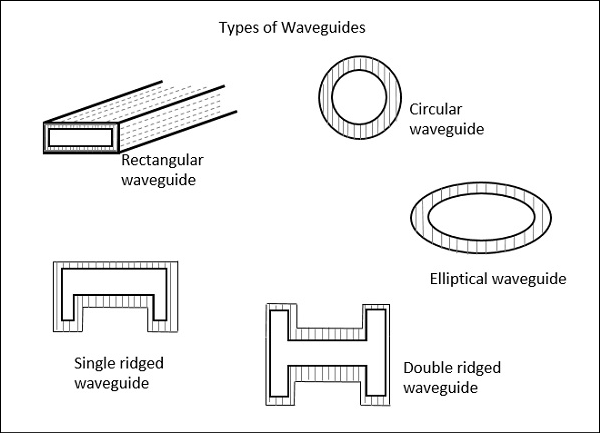
Les types de guides d'ondes illustrés ci-dessus sont creux au centre et constitués de parois en cuivre. Ceux-ci ont une fine couche d'Au ou d'Ag sur la surface intérieure.
Comparons maintenant les lignes de transmission et les guides d'ondes.
Lignes de transmission vs guides d'ondes
La principale différence entre une ligne de transmission et un guide d'ondes est -
UNE two conductor structure qui peut supporter une onde TEM est une ligne de transmission.
UNE one conductor structure qui peut supporter une onde TE ou une onde TM mais pas une onde TEM est appelée guide d'ondes.
Le tableau suivant met en évidence les différences entre les lignes de transmission et les guides d'ondes.
| Lignes de transmission | Guides d'ondes |
|---|---|
| Prend en charge la vague TEM | Ne peut pas prendre en charge la vague TEM |
| Toutes les fréquences peuvent passer | Seules les fréquences supérieures à la fréquence de coupure peuvent passer |
| Transmission à deux conducteurs | Transmission à un conducteur |
| Les reflets sont moins | Une onde traverse les réflexions des parois du guide d'ondes |
| Il a une impédance caractéristique | Il a une impédance d'onde |
| La propagation des ondes est conforme à la "théorie des circuits" | La propagation des ondes est conforme à la "théorie des champs" |
| Il a un conducteur de retour à la terre | Le conducteur de retour n'est pas nécessaire car le corps du guide d'ondes fait office de terre |
| La bande passante n'est pas limitée | La bande passante est limitée |
| Les vagues ne se dispersent pas | Les vagues se dispersent |
Vitesse de phase
La vitesse de phase est la vitesse à laquelle l'onde change de phase pour subir un déphasage de 2πradians. Il peut être compris comme le changement de vitesse des composantes d'onde d'une onde sinusoïdale, lorsqu'elle est modulée.
Dérivons une équation pour la vitesse de phase.
Selon la définition, le taux de changement de phase à 2π radians doit être pris en compte.
Ce qui signifie, $λ$ / $T$ Par conséquent,
$$ V = \ frac {\ lambda} {T} $$
Où,
$ λ $ = longueur d'onde et $ T $ = temps
$$ V = \ frac {\ lambda} {T} = \ lambda f $$
Puisque $ f = \ frac {1} {T} $
Si nous multiplions le numérateur et le dénominateur par 2π ensuite nous avons
$$ V = \ lambda f = \ frac {2 \ pi \ lambda f} {2 \ pi} $$
On sait que $ \ omega = 2 \ pi f $ and $ \ beta = \ frac {2 \ pi} {f} $
L'équation ci-dessus peut être écrite comme suit:
$$ V = \ frac {2 \ pi f} {\ frac {2 \ pi} {\ lambda}} = \ frac {\ omega} {\ beta} $$
Par conséquent, l'équation de la vitesse de phase est représentée par
$$ V_p = \ frac {\ omega} {\ beta} $$
Vitesse de groupe
La vitesse de groupe peut être définie comme la vitesse à laquelle l'onde se propage à travers le guide d'ondes. Cela peut être compris comme la vitesse à laquelle une enveloppe modulée se déplace par rapport à la porteuse seule. Cette onde modulée parcourt le guide d'ondes.
L'équation de la vitesse de groupe est représentée par
$$ V_g = \ frac {d \ omega} {d \ beta} $$
La vitesse de l'enveloppe modulée est généralement plus lente que le signal porteur.
Dans ce chapitre, nous discuterons des composants micro-ondes tels que les transistors micro-ondes et les différents types de diodes.
Transistors micro-ondes
Il est nécessaire de développer des transistors spéciaux pour tolérer les fréquences micro-ondes. Par conséquent pour les applications micro-ondes,silicon n-p-n transistorsqui peuvent fournir des puissances adéquates aux fréquences micro-ondes ont été développés. Ils ont généralement 5 watts à une fréquence de 3 GHz avec un gain de 5 dB. Une vue en coupe d'un tel transistor est représentée sur la figure suivante.
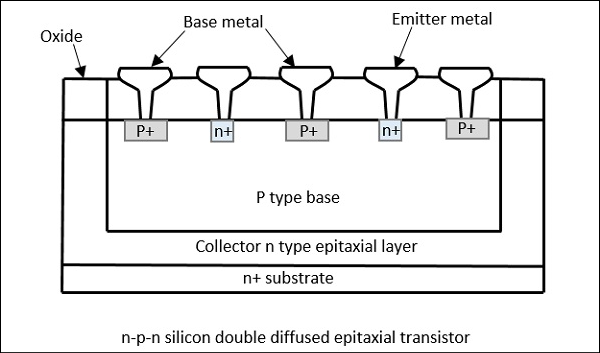
Construction de transistors hyperfréquences
Un n type couche épitaxiale est cultivée sur n+substrat constituant le collecteur. Sur cenrégion, une couche de SiO2 est développée thermiquement. UNEp-base et fortement dopé n-emitterssont diffusés dans la base. Les ouvertures sont réalisées en oxyde pour les contacts ohmiques. Les connexions se font en parallèle.
Ces transistors ont une géométrie de surface catégorisée comme interdigitée, superposée ou matricielle. Ces formulaires sont illustrés dans la figure suivante.
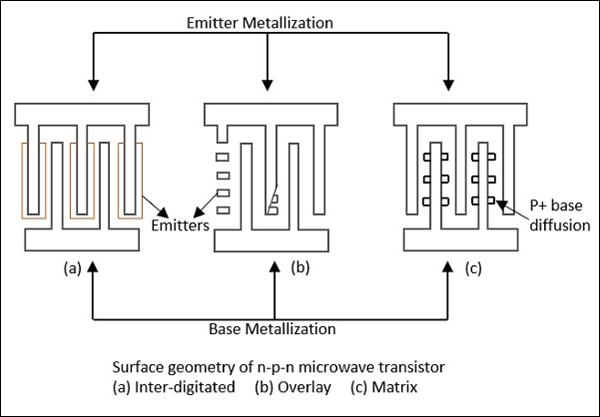
Les transistors de puissance utilisent les trois géométries de surface.
Les petits transistors de signal utilisent une géométrie de surface interdigitée. La structure interdigitée convient aux applications de petits signaux dans les bandes L, S et C.
La géométrie de la matrice est parfois appelée maillage ou grille d'émetteur. Les structures Overlay et Matrix sont utiles comme dispositifs d'alimentation dans les régions UHF et VHF.
Fonctionnement des transistors hyperfréquences
Dans un transistor hyperfréquence, initialement les jonctions émetteur-base et collecteur-base sont polarisées en inverse. Lors de l'application d'un signal hyperfréquence, la jonction émetteur-base devient polarisée en direct. Si unp-n-ptransistor est considéré, l'application d'un pic positif de signal, polarise en direct la jonction émetteur-base, faisant dériver les trous vers la base négative mince. Les trous accélèrent en outre vers la borne négative de la tension de polarisation entre le collecteur et les bornes de base. Une charge connectée au collecteur, reçoit une impulsion de courant.
Dispositifs à semi-conducteurs
La classification des appareils à micro-ondes à semi-conducteurs peut être effectuée -
En fonction de leur comportement électrique
-
Type de résistance non linéaire.
Exemple - Varistances (résistances variables)
-
Type de réactance non linéaire.
Exemple - Varactors (réacteurs variables)
-
Type de résistance négative.
Exemple - Diode tunnel, diode Impatt, diode Gunn
-
Type d'impédance contrôlable.
Exemple - diode PIN
-
- En fonction de leur construction
- Diodes de contact ponctuel
- Diodes barrières Schottky
- Dispositifs à semi-conducteurs à oxyde métallique (MOS)
- Dispositifs d'isolation en métal
Les types de diodes que nous avons mentionnés ici ont de nombreuses utilisations telles que l'amplification, la détection, la génération d'énergie, le déphasage, la conversion descendante, la conversion ascendante, la modulation de limitation, la commutation, etc.
Diode Varactor
Une capacité variable de tension d'une jonction polarisée en inverse peut être appelée diode Varactor. La diode varactor est un dispositif semi-conducteur dans lequel la capacité de jonction peut être modifiée en fonction de la polarisation inverse de la diode. Les caractéristiques CV d'une diode Varactor typique et ses symboles sont illustrés dans la figure suivante.
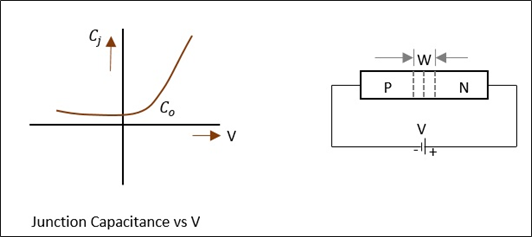
La capacité de jonction dépend de la tension appliquée et de la conception de la jonction. Nous savons que,
$$ C_j \: \ alpha \: V_ {r} ^ {- n} $$
Où
$ C_j $ = Capacité de jonction
$ V_r $ = tension de polarisation inverse
$n$ = Un paramètre qui décide du type de jonction
Si la jonction est polarisée en inverse, les porteurs mobiles appauvrissent la jonction, ce qui entraîne une certaine capacité, où la diode se comporte comme un condensateur, la jonction agissant comme un diélectrique. La capacité diminue avec l'augmentation de la polarisation inverse.
L'encapsulation de la diode contient des conducteurs électriques qui sont attachés à la tranche de semi-conducteur et un conducteur attaché au boîtier en céramique. La figure suivante montre à quoi ressemble une diode Varactor micro-ondes.
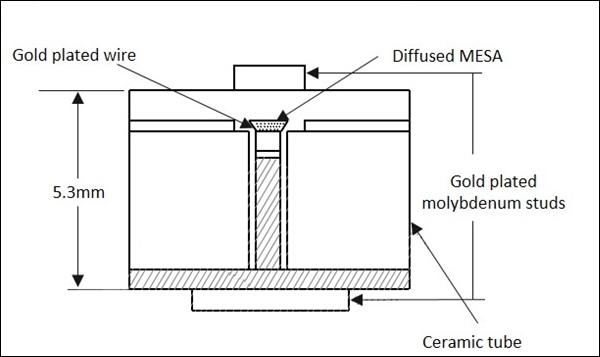
Ceux-ci sont capables de gérer de grandes puissances et de grandes tensions de claquage inversées. Ceux-ci ont un faible bruit. Bien que la variation de la capacité de jonction soit un facteur important dans cette diode, des résistances parasites, des capacités et des conductances sont associées à chaque diode pratique, qui doit être maintenue faible.
Applications de la diode Varactor
Les diodes Varactor sont utilisées dans les applications suivantes -
- Conversion ascendante
- Amplificateur paramétrique
- Génération d'impulsions
- Mise en forme d'impulsion
- Circuits de commutation
- Modulation des signaux micro-ondes
Diode de barrière Schottky
Il s'agit d'une simple diode qui présente une impédance non linéaire. Ces diodes sont principalement utilisées pour la détection et le mélange de micro-ondes.
Construction de la diode de barrière Schottky
Une pastille semi-conductrice est montée sur une base métallique. Un fil à ressort est connecté avec une pointe acérée à cette pastille de silicium. Ceci peut être facilement monté dans des lignes coaxiales ou guides d'ondes. La figure suivante donne une image claire de la construction.
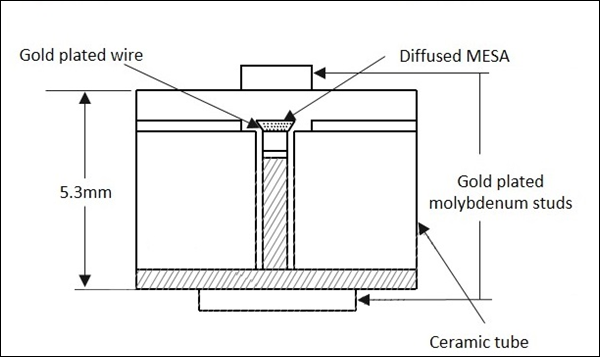
Fonctionnement de la diode de barrière Schottky
Avec le contact entre le semi-conducteur et le métal, une région d'appauvrissement est formée. La région métallique a une largeur d'appauvrissement plus petite, comparativement. Lorsqu'un contact est établi, un flux d'électrons se produit du semi-conducteur vers le métal. Cet épuisement crée une charge d'espace positive dans le semi-conducteur et le champ électrique s'oppose à un écoulement supplémentaire, ce qui conduit à la création d'une barrière à l'interface.
Pendant la polarisation directe, la hauteur de la barrière est réduite et les électrons sont injectés dans le métal, tandis que pendant la polarisation inverse, la hauteur de la barrière augmente et l'injection d'électrons s'arrête presque.
Avantages de la diode de barrière Schottky
Voici les avantages suivants.
- À bas prix
- Simplicity
- Reliable
- Chiffres de bruit 4 à 5 dB
Applications de la diode de barrière Schottky
Ce sont les applications suivantes.
- Mélangeur à faible bruit
- Mélangeur équilibré en radar à ondes continues
- Détecteur micro-ondes
Dispositifs à effet Gunn
JB Gunn a découvert des fluctuations périodiques du courant traversant le n-type GaAséchantillon lorsque la tension appliquée dépasse une certaine valeur critique. Dans ces diodes, il y a deux vallées,L & U valleysen bande de conduction et le transfert d'électrons se produit entre eux, en fonction du champ électrique appliqué. Cet effet de l'inversion de la population de la vallée inférieure L à la vallée supérieure U est appeléTransfer Electron Effect et donc ceux-ci sont appelés comme Transfer Electron Devices (TED).
Applications des diodes Gunn
Les diodes Gunn sont largement utilisées dans les appareils suivants -
- Émetteurs radar
- Transpondeurs dans le contrôle du trafic aérien
- Systèmes de télémétrie industriels
- Oscillateurs de puissance
- Circuits logiques
- Amplificateur linéaire à large bande
On dit que le processus d'avoir un retard entre la tension et le courant, en avalanche avec le temps de transit, à travers le matériau, est une résistance négative. Les dispositifs qui aident à faire une diode présentent cette propriété sont appelés commeAvalanche transit time devices.
Les exemples d'appareils qui entrent dans cette catégorie sont les diodes IMPATT, TRAPATT et BARITT. Jetons un coup d'œil à chacun d'eux, en détail.
Diode IMPATT
Il s'agit d'une diode semi-conductrice haute puissance, utilisée dans les applications hyperfréquences haute fréquence. Le formulaire complet IMPATT estIMPact ionization Avalanche Transit Time diode.
Un gradient de tension lorsqu'il est appliqué à la diode IMPATT, se traduit par un courant élevé. Une diode normale finira par se décomposer par cela. Cependant, la diode IMPATT est développée pour résister à tout cela. Un gradient de potentiel élevé est appliqué pour polariser en retour la diode et donc des porteurs minoritaires circulent à travers la jonction.
L'application d'une tension alternative RF si elle est superposée à une tension continue élevée, la vitesse accrue des trous et des électrons entraîne des trous et des électrons supplémentaires en les expulsant de la structure cristalline par ionisation par impact. Si le champ DC d'origine appliqué était au seuil de développement de cette situation, alors il conduit à la multiplication du courant d'avalanche et ce processus se poursuit. Cela peut être compris par la figure suivante.
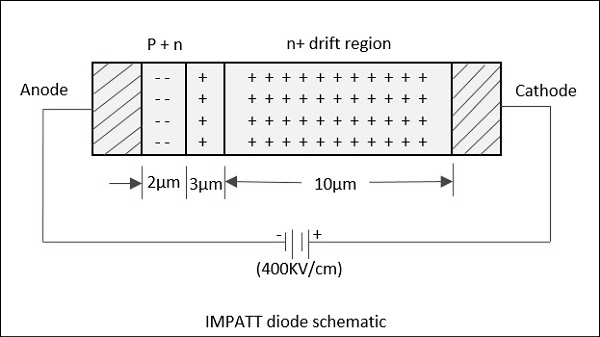
En raison de cet effet, l'impulsion de courant prend un déphasage de 90 °. Cependant, au lieu d'être là, il se déplace vers la cathode en raison de la polarisation inverse appliquée. Le temps nécessaire à l'impulsion pour atteindre la cathode dépend de l'épaisseur den+couche, qui est ajustée pour faire un déphasage de 90 °. Maintenant, il est prouvé qu'une résistance négative RF dynamique existe. Par conséquent, la diode IMPATT agit à la fois comme un oscillateur et un amplificateur.
La figure suivante montre les détails de construction d'une diode IMPATT.

L'efficacité de la diode IMPATT est représentée par
$$ \ eta = \ left [\ frac {P_ {ac}} {P_ {dc}} \ right] = \ frac {V_a} {V_d} \ left [\ frac {I_a} {I_d} \ right] $$
Où,
$ P_ {ac} $ = alimentation CA
$ P_ {dc} $ = alimentation CC
$ V_a \: \ & \: I_a $ = tension et courant alternatifs
$ V_d \: \ & \: I_d $ = tension et courant CC
Désavantages
Voici les inconvénients de la diode IMPATT.
- C'est bruyant car l'avalanche est un processus bruyant
- La plage de réglage n'est pas aussi bonne que dans les diodes Gunn
Applications
Voici les applications de la diode IMPATT.
- Oscillateur micro-ondes
- Générateurs micro-ondes
- Oscillateur de sortie modulé
- Oscillateur local du récepteur
- Amplifications de résistance négative
- Réseaux d'alarme intrusion (Q IMPATT élevé)
- Radar de police (Q IMPATT élevé)
- Émetteur micro-ondes de faible puissance (Q IMPATT élevé)
- Émetteur de télécommunication FM (faible Q IMPATT)
- Émetteur radar Doppler CW (faible Q IMPATT)
Diode TRAPATT
La forme complète de la diode TRAPATT est TRApped Plasma Avalanche Triggered Transit diode. Un générateur de micro-ondes qui fonctionne entre des centaines de MHz et GHz. Ce sont généralement des diodes de puissance de crête élevéen+- p-p+ ou p+-n-n+structures avec région d'appauvrissement de type n, largeur variant de 2,5 à 1,25 µm. La figure suivante illustre cela.
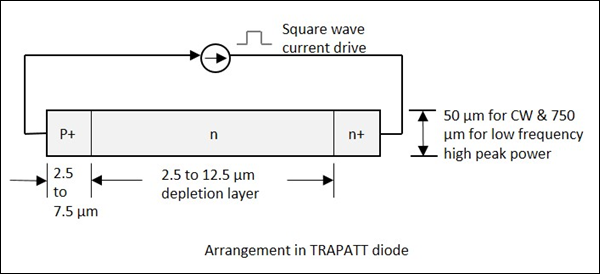
Les électrons et les trous piégés dans la région de champ bas derrière la zone, sont faits pour remplir la région d'appauvrissement dans la diode. Ceci est fait par une région d'avalanche à champ élevé qui se propage à travers la diode.
La figure suivante montre un graphique dans lequel AB montre la charge, BC montre la formation de plasma, DE montre l'extraction au plasma, EF montre l'extraction résiduelle et FG montre la charge.
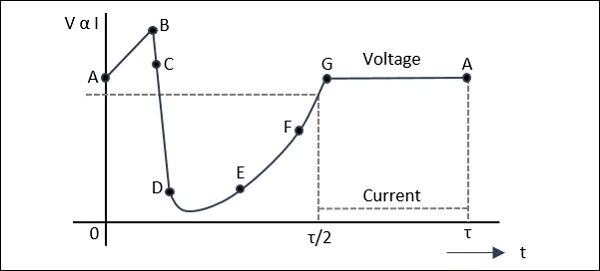
Voyons ce qui se passe à chacun des points.
A:La tension au point A n'est pas suffisante pour que la panne d'avalanche se produise. En A, les porteurs de charge dus à la génération thermique entraînent la charge de la diode comme une capacité linéaire.
A-B:À ce stade, la magnitude du champ électrique augmente. Lorsqu'un nombre suffisant de porteurs est généré, le champ électrique est abaissé dans toute la région d'appauvrissement, provoquant une diminution de la tension de B à C.
C:Cette charge aide l'avalanche à se poursuivre et un plasma dense d'électrons et de trous est créé. Le champ est en outre abaissé afin de ne pas laisser les électrons ou les trous hors de la couche d'appauvrissement, et emprisonne le plasma restant.
D: La tension diminue au point D. Un temps long est nécessaire pour effacer le plasma car la charge totale du plasma est importante par rapport à la charge par unité de temps dans le courant externe.
E:Au point E, le plasma est éliminé. Des charges résiduelles de trous et d'électrons restent chacune à une extrémité de la couche de déflexion.
E to F: La tension augmente à mesure que la charge résiduelle est éliminée.
F: Au point F, toute la charge générée en interne est supprimée.
F to G: La diode se charge comme un condensateur.
G:Au point G, le courant de la diode est nul pendant une demi-période. La tension reste constante comme indiqué dans le graphique ci-dessus. Cet état continue jusqu'à ce que le courant revienne et que le cycle se répète.
La vitesse de la zone d'avalanche $ V_s $ est représentée par
$$ V_s = \ frac {dx} {dt} = \ frac {J} {qN_A} $$
Où
$J$ = Densité de courant
$q$= Charge d'électrons 1,6 x 10-19
$ N_A $ = concentration de dopage
La zone d'avalanche balayera rapidement la majeure partie de la diode et le temps de transit des porteurs est représenté par
$$ \ tau_s = \ frac {L} {V_s} $$
Où
$ V_s $ = vitesse de dérive saturée de la porteuse
$ L $ = Longueur du spécimen
Le temps de transit calculé ici est le temps entre l'injection et la collecte. L'action répétée augmente la sortie pour en faire un amplificateur, alors qu'un filtre passe-bas hyperfréquence connecté en shunt avec le circuit peut le faire fonctionner comme un oscillateur.
Applications
Il existe de nombreuses applications de cette diode.
- Radars Doppler basse puissance
- Oscillateur local pour radars
- Système d'atterrissage de balise à micro-ondes
- Radioaltimètre
- Radar à réseau de phase, etc.
Diode BARITT
La forme complète de BARITT Diode is BARrier Injection Transit Time diode. Ce sont la dernière invention de cette famille. Bien que ces diodes aient de longues régions de dérive comme les diodes IMPATT, l'injection de porteurs dans les diodes BARITT est provoquée par des jonctions polarisées en direct, mais pas à partir du plasma d'une région d'avalanche comme dans celles-ci.
Dans les diodes IMPATT, l'injection de porteurs est assez bruyante en raison de l'ionisation par impact. Dans les diodes BARITT, pour éviter le bruit, l'injection de porteurs est fournie par perforation de la région d'appauvrissement. La résistance négative dans une diode BARITT est obtenue du fait de la dérive des trous injectés vers l'extrémité collecteur de la diode, en matériau de type p.
La figure suivante montre les détails de construction d'une diode BARITT.
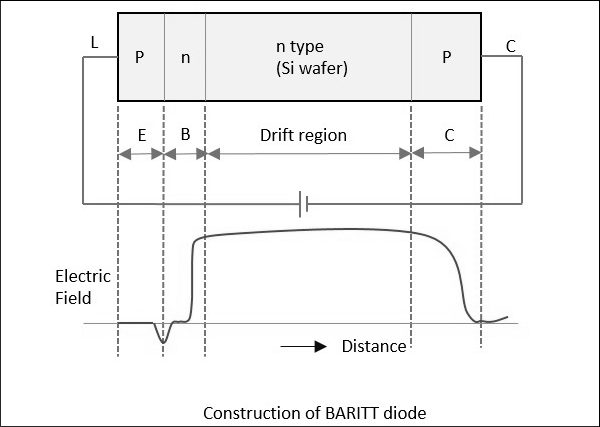
Pour un m-n-m Diode BARITT, Ps-Si La barrière Schottky entre en contact avec les métaux n-type Si waferentre. Une augmentation rapide du courant avec la tension appliquée (supérieure à 30 V) est due à l'injection de trous thermioniques dans le semi-conducteur.
La tension critique $ (Vc) $ dépend de la constante de dopage $ (N) $, de la longueur du semi-conducteur $ (L) $ et de la permittivité diélectrique du semi-conducteur $ (\ epsilon S) $ représentée par
$$ V_c = \ frac {qNL ^ 2} {2 \ epsilon S} $$
Circuit intégré hyperfréquence monolithique (MMIC)
Les circuits intégrés hyperfréquences sont la meilleure alternative aux guides d'ondes conventionnels ou aux circuits coaxiaux, car ils sont de faible poids, de petite taille, hautement fiables et reproductibles. Les matériaux de base utilisés pour les circuits intégrés hyperfréquences monolithiques sont:
- Matériau du substrat
- Matériau du conducteur
- Films diélectriques
- Films résistifs
Ceux-ci sont ainsi choisis pour avoir des caractéristiques idéales et un rendement élevé. Le substrat sur lequel les éléments de circuit sont fabriqués est important car la constante diélectrique du matériau doit être élevée avec un faible facteur de dissipation, ainsi que d'autres caractéristiques idéales. Les matériaux de substrat utilisés sont GaAs, ferrite / grenat, aluminium, béryllium, verre et rutile.
Le matériau conducteur est ainsi choisi pour avoir une conductivité élevée, un coefficient de résistance à basse température, une bonne adhérence au substrat et à la gravure, etc. L'aluminium, le cuivre, l'or et l'argent sont principalement utilisés comme matériaux conducteurs. Les matériaux diélectriques et les matériaux résistifs sont ainsi choisis pour avoir une faible perte et une bonne stabilité.
Technologie de fabrication
Dans les circuits intégrés hybrides, les dispositifs semi-conducteurs et les éléments de circuit passifs sont formés sur un substrat diélectrique. Les circuits passifs sont des éléments distribués ou localisés, ou une combinaison des deux.
Les circuits intégrés hybrides sont de deux types.
- IC hybride
- Circuit intégré hybride miniature
Dans les deux processus ci-dessus, le circuit intégré hybride utilise les éléments de circuit distribués qui sont fabriqués sur le circuit intégré en utilisant une technique de métallisation monocouche, tandis que le circuit intégré hybride miniature utilise des éléments à plusieurs niveaux.
La plupart des circuits analogiques utilisent la technologie de méso-isolation pour isoler les zones actives de type n utilisées pour les FET et les diodes. Les circuits plans sont fabriqués en implantant des ions dans un substrat semi-isolant, et pour assurer l'isolation, les zones sont masquées.
"Via hole"La technologie est utilisée pour connecter la source avec des électrodes de source connectées à la terre, dans un FET GaAs, comme illustré dans la figure suivante.

Il existe de nombreuses applications des MMIC.
- Communication militaire
- Radar
- ECM
- Systèmes d'antennes à réseau de phase
- Spread Spectrum et systèmes TDMA
Ils sont rentables et également utilisés dans de nombreuses applications de consommation domestique telles que DTH, télécommunications et instrumentation, etc.
Tout comme les autres systèmes, les systèmes hyperfréquences se composent de nombreux composants hyperfréquences, principalement avec une source à une extrémité et une charge à l'autre, qui sont tous connectés avec des guides d'ondes ou des systèmes de câbles coaxiaux ou de lignes de transmission.
Voici les propriétés des guides d'ondes.
- SNR élevé
- Faible atténuation
- Moins de perte d'insertion
Fonctions micro-ondes du guide d'ondes
Considérez un guide d'ondes ayant 4 ports. Si l'alimentation est appliquée à un port, elle passe par les 3 ports dans certaines proportions où une partie peut être réfléchie par le même port. Ce concept est clairement illustré dans la figure suivante.
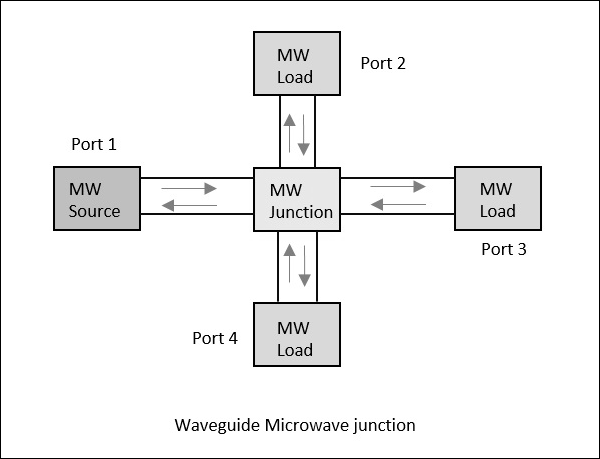
Paramètres de diffusion
Pour un réseau à deux ports, comme le montre la figure suivante, si l'alimentation est appliquée à un port, comme nous venons de le dire, la plupart de l'alimentation s'échappe de l'autre port, tandis qu'une partie est renvoyée vers le même port. Dans la figure suivante, siV1 ou V2 est appliqué, alors I1 ou I2 le courant circule respectivement.
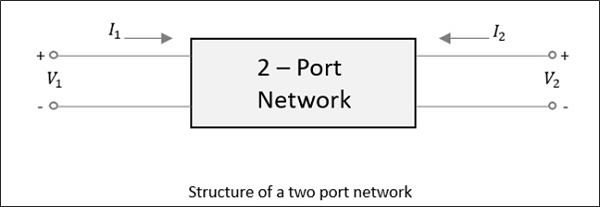
Si la source est appliquée au port opposé, deux autres combinaisons doivent être envisagées. Ainsi, pour un réseau à deux ports, 2 × 2 = 4 combinaisons sont susceptibles de se produire.
Les ondes progressives avec les puissances associées lorsqu'elles se dispersent à travers les ports, la jonction hyperfréquence peut être définie par des paramètres S ou Scattering Parameters, qui sont représentés sous une forme matricielle, appelée "Scattering Matrix".
Matrice de dispersion
C'est une matrice carrée qui donne toutes les combinaisons de relations de puissance entre les différents ports d'entrée et de sortie d'une jonction hyperfréquence. Les éléments de cette matrice sont appelés"Scattering Coefficients" ou "Scattering (S) Parameters".
Considérez la figure suivante.

Ici, la source est connectée via la ligne $ i ^ {th} $ tandis que $ a_1 $ est l'onde incidente et $ b_1 $ est l'onde réfléchie.
Si une relation est donnée entre $ b_1 $ et $ a_1 $,
$$ b_1 = (réflexion \: \: coefficient) a_1 = S_ {1i} a_1 $$
Où
$ S_ {1i} $ = Coefficient de réflexion de $ 1 ^ {st} $ line (où $ i $ est le port d'entrée et $ 1 $ est le port de sortie)
$ 1 $ = Réflexion de la ligne $ 1 ^ {st} $
$ i $ = Source connectée à la ligne $ i ^ {th} $
Si l'impédance correspond, la puissance est transférée à la charge. Peu probable, si l'impédance de charge ne correspond pas à l'impédance caractéristique. Ensuite, la réflexion se produit. Cela signifie que la réflexion se produit si
$$ Z_l \ neq Z_o $$
Cependant, si cette discordance existe pour plus d'un port, par exemple $ 'n' $ ports, alors $ i = 1 $ à $ n $ (puisque $ i $ peut être n'importe quelle ligne de $ 1 $ à $ n $).
Par conséquent, nous avons
$$ b_1 = S_ {11} a_1 + S_ {12} a_2 + S_ {13} a_3 + ............... + S_ {1n} a_n $$
$$ b_2 = S_ {21} a_1 + S_ {22} a_2 + S_ {23} a_3 + ............... + S_ {2n} a_n $$
$$. $$
$$. $$
$$. $$
$$. $$
$$. $$
$$ b_n = S_ {n1} a_1 + S_ {n2} a_2 + S_ {n3} a_3 + ............... + S_ {nn} a_n $$
Lorsque tout cela est conservé sous forme de matrice,
$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \\. \\. \\. \\ b_n \ end {bmatrix} = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13 } & ... & S_ {1n} \\ S_ {21} & S_ {22} & S_ {23} & ... & S_ {2n} \\. &. &. & ... &. \\. &. &. & ... &. \\. &. &. & ... &. \\ S_ {n1} & S_ {n2} & S_ {n3} & ... & S_ {nn} \\ \ end {bmatrix} \ times \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \\. \ \. \\. \\ a_n \ end {bmatrix} $$
Column matrix $ [b] $ Scattering matrix $ [S] $Matrix $ [a] $
La matrice colonne $ \ left [b \ right] $ correspond aux ondes réfléchies ou à la sortie, tandis que la matrice $ \ left [a \ right] $ correspond aux ondes incidentes ou à l'entrée. La matrice de colonnes de diffusion $ \ left [s \ right] $ qui est de l'ordre de $ n \ fois n $ contient les coefficients de réflexion et de transmission. Par conséquent,
$$ \ left [b \ right] = \ left [S \ right] \ left [a \ right] $$
Propriétés de [S] Matrix
La matrice de diffusion est indiquée par $ [S] $ matrix. Il existe peu de propriétés standard pour la matrice $ [S] $. Ils sont -
-
$ [S] $ est toujours une matrice carrée d'ordre (nxn)
$ [S] _ {n \ fois n} $
-
$ [S] $ est une matrice symétrique
c'est-à-dire, $ S_ {ij} = S_ {ji} $
-
$ [S] $ est une matrice unitaire
c'est-à-dire $ [S] [S] ^ * = I $
La somme des produits de chaque terme de toute ligne ou colonne multipliée par le conjugué complexe des termes correspondants de toute autre ligne ou colonne est égale à zéro. c'est à dire,
$$ \ sum_ {i = j} ^ {n} S_ {ik} S_ {ik} ^ {*} = 0 \: pour \: k \ neq j $$
$$ (k = 1,2,3, ... \: n) \: et \: (j = 1,2,3, ... \: n) $$
-
Si la distance électrique entre un port $ k ^ {th} $ et la jonction est $ \ beta _kI_k $, alors les coefficients de $ S_ {ij} $ impliquant $ k $, seront multipliés par le facteur $ e ^ {- j \ beta kIk} $
Dans les prochains chapitres, nous examinerons différents types de jonctions micro-ondes en T.
Une jonction en T E-Plane est formée en attachant un simple guide d'ondes à la dimension plus large d'un guide d'ondes rectangulaire, qui a déjà deux ports. Les bras des guides d'ondes rectangulaires font deux ports appeléscollinear ports c'est-à-dire, Port1 et Port2, tandis que le nouveau, Port3 est appelé comme bras latéral ou E-arm. Ce tee-shirt E-plane est également appeléSeries Tee.
Comme l'axe du bras latéral est parallèle au champ électrique, cette jonction est appelée jonction E-Plane Tee. Ceci est également appelé commeVoltage ou Series junction. Les ports 1 et 2 sont déphasés de 180 ° l'un par rapport à l'autre. Les détails de la section transversale du té E-plan peuvent être compris par la figure suivante.
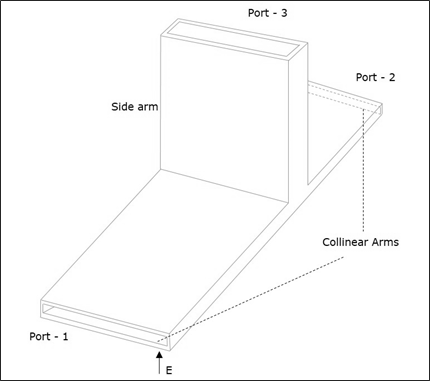
La figure suivante montre la connexion établie par l'arme de poing au guide d'ondes bidirectionnel pour former le port parallèle.
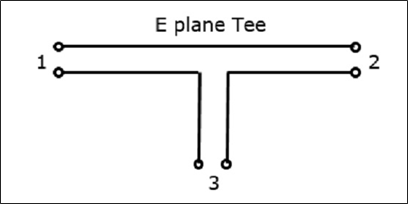
Propriétés de E-Plane Tee
Les propriétés de E-Plane Tee peuvent être définies par sa matrice $ [S] _ {3x3} $.
C'est une matrice 3 × 3 car il y a 3 entrées possibles et 3 sorties possibles.
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {21} & S_ {22} & S_ {23} \\ S_ {31} & S_ {32 } & S_ {33} \ end {bmatrix} $ ........ Equation 1
Les coefficients de diffusion $ S_ {13} $ et $ S_ {23} $ sont déphasés de 180 ° avec une entrée au port 3.
$ S_ {23} = -S_ {13} $........ Equation 2
Le port est parfaitement adapté à la jonction.
$ S_ {33} = 0 $........ Equation 3
De la propriété symétrique,
$ S_ {ij} = S_ {ji} $
$ S_ {12} = S_ {21} \: \: S_ {23} = S_ {32} \: \: S_ {13} = S_ {31} $........ Equation 4
En considérant les équations 3 et 4, la matrice $ [S] $ peut être écrite comme suit:
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & -S_ {13} \\ S_ {13} & -S_ {13} & 0 \ end {bmatrix} $........ Equation 5
Nous pouvons dire que nous avons quatre inconnues, compte tenu de la propriété de symétrie.
De la propriété unitaire
$$ [S] [S] \ ast = [I] $$
$$ \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & -S_ {13} \\ S_ {13} & -S_ {13} & 0 \ end {bmatrix} \: \ begin {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} & S_ {13} ^ {*} \\ S_ {12} ^ {*} & S_ {22} ^ {*} & -S_ {13} ^ {*} \\ S_ {13} ^ {*} & -S_ {13} ^ {*} & 0 \ end {bmatrix} = \ begin { bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
En multipliant nous obtenons,
(Notant R comme ligne et C comme colonne)
$ R_1C_1: S_ {11} S_ {11} ^ {*} + S_ {12} S_ {12} ^ {*} + S_ {13} S_ {13} ^ {*} = 1 $
$ \ gauche | S_ {11} \ droite | ^ 2 + \ gauche | S_ {11} \ droite | ^ 2 + \ gauche | S_ {11} \ droite | ^ 2 = 1 $........ Equation 6
$ R_2C_2: \ gauche | S_ {12} \ droite | ^ 2 + \ gauche | S_ {22} \ droite | ^ 2 + \ gauche | S_ {13} \ droite | ^ 2 = 1 $......... Equation 7
$ R_3C_3: \ gauche | S_ {13} \ droite | ^ 2 + \ gauche | S_ {13} \ droite | ^ 2 = 1 $......... Equation 8
$ R_3C_1: S_ {13} S_ {11} ^ {*} - S_ {13} S_ {12} ^ {*} = 1 $ ......... Equation 9
En égalant les équations 6 et 7, nous obtenons
$ S_ {11} = S_ {22} $ ......... Equation 10
De l'équation 8,
$ 2 \ gauche | S_ {13} \ right | ^ 2 \ quad ou \ quad S_ {13} = \ frac {1} {\ sqrt {2}} $......... Equation 11
D'après l'équation 9,
$ S_ {13} \ gauche (S_ {11} ^ {*} - S_ {12} ^ {*} \ droite) $
Ou $ S_ {11} = S_ {12} = S_ {22} $ ......... Equation 12
En utilisant les équations 10, 11 et 12 de l'équation 6,
on a,
$ \ gauche | S_ {11} \ droite | ^ 2 + \ gauche | S_ {11} \ right | ^ 2 + \ frac {1} {2} = 1 $
$ 2 \ gauche | S_ {11} \ right | ^ 2 = \ frac {1} {2} $
Ou $ S_ {11} = \ frac {1} {2} $ ......... Equation 13
En substituant les valeurs des équations ci-dessus dans la matrice $ [S] $,
On a,
$$ \ left [S \ right] = \ begin {bmatrix} \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac { 1} {2} & \ frac {1} {2} & - \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & - \ frac {1} { \ sqrt {2}} & 0 \ end {bmatrix} $$
Nous savons que $ [b] $ = $ [S] [a] $
$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \ end {bmatrix} = \ begin {bmatrix} \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {2} & \ frac {1} {2} & - \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2 }} & - \ frac {1} {\ sqrt {2}} & 0 \ end {bmatrix} \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \ end {bmatrix} $$
C'est la matrice de diffusion pour E-Plane Tee, ce qui explique ses propriétés de diffusion.
Une jonction en T H-Plane est formée en attachant un simple guide d'ondes à un guide d'ondes rectangulaire qui a déjà deux ports. Les bras des guides d'ondes rectangulaires font deux ports appeléscollinear ports c'est-à-dire, Port1 et Port2, tandis que le nouveau, Port3 est appelé comme bras latéral ou H-arm. Ce tee-shirt H-plane est également appeléShunt Tee.
Comme l'axe du bras latéral est parallèle au champ magnétique, cette jonction est appelée jonction H-Plane Tee. Ceci est également appelé commeCurrent junction, alors que le champ magnétique se divise en bras. Les détails de la section transversale du té plan H peuvent être compris par la figure suivante.

La figure suivante montre la connexion établie par l'arme de poing au guide d'ondes bidirectionnel pour former le port série.
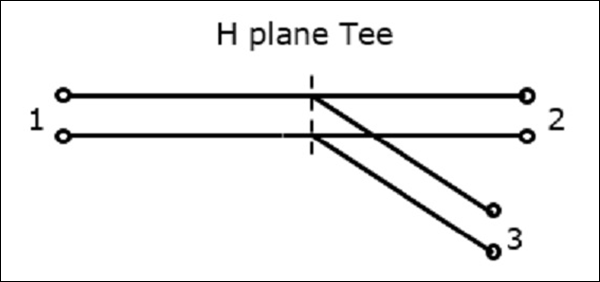
Propriétés de H-Plane Tee
Les propriétés de H-Plane Tee peuvent être définies par sa matrice $ \ left [S \ right] _ {3 \ times 3} $.
C'est une matrice 3 × 3 car il y a 3 entrées possibles et 3 sorties possibles.
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {21} & S_ {22} & S_ {23} \\ S_ {31} & S_ {32 } & S_ {33} \ end {bmatrix} $ ........ Equation 1
Les coefficients de diffusion $ S_ {13} $ et $ S_ {23} $ sont ici égaux car la jonction est symétrique dans le plan.
De la propriété symétrique,
$ S_ {ij} = S_ {ji} $
$ S_ {12} = S_ {21} \: \: S_ {23} = S_ {32} = S_ {13} \: \: S_ {13} = S_ {31} $
Le port est parfaitement assorti
$ S_ {33} = 0 $
Maintenant, la matrice $ [S] $ peut s'écrire comme,
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & S_ {13} \\ S_ {13} & S_ {13 } & 0 \ end {bmatrix} $ ........ Equation 2
Nous pouvons dire que nous avons quatre inconnues, compte tenu de la propriété de symétrie.
De la propriété unitaire
$$ [S] [S] \ ast = [I] $$
$$ \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & S_ {13} \\ S_ {13} & S_ {13} & 0 \ end {bmatrix} \: \ begin {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} & S_ {13} ^ {*} \\ S_ {12} ^ {*} & S_ {22} ^ {*} & S_ {13} ^ {*} \\ S_ {13} ^ {*} & S_ {13} ^ {*} & 0 \ end {bmatrix} = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
En multipliant nous obtenons,
(Notant R comme ligne et C comme colonne)
$ R_1C_1: S_ {11} S_ {11} ^ {*} + S_ {12} S_ {12} ^ {*} + S_ {13} S_ {13} ^ {*} = 1 $
$ \ gauche | S_ {11} \ droite | ^ 2 + \ gauche | S_ {12} \ droite | ^ 2 + \ gauche | S_ {13} \ droite | ^ 2 = 1 $........ Equation 3
$ R_2C_2: \ gauche | S_ {12} \ droite | ^ 2 + \ gauche | S_ {22} \ droite | ^ 2 + \ gauche | S_ {13} \ droite | ^ 2 = 1 $......... Equation 4
$ R_3C_3: \ gauche | S_ {13} \ droite | ^ 2 + \ gauche | S_ {13} \ droite | ^ 2 = 1 $......... Equation 5
$ R_3C_1: S_ {13} S_ {11} ^ {*} - S_ {13} S_ {12} ^ {*} = 0 $ ......... Equation 6
$ 2 \ gauche | S_ {13} \ right | ^ 2 = 1 \ quad ou \ quad S_ {13} = \ frac {1} {\ sqrt {2}} $......... Equation 7
$ \ gauche | S_ {11} \ droite | ^ 2 = \ gauche | S_ {22} \ droite | ^ 2 $
$ S_ {11} = S_ {22} $ ......... Equation 8
À partir de l'équation 6, $ S_ {13} \ left (S_ {11} ^ {*} + S_ {12} ^ {*} \ right) = 0 $
Depuis, $ S_ {13} \ neq 0, S_ {11} ^ {*} + S_ {12} ^ {*} = 0, \: ou \: S_ {11} ^ {*} = -S_ {12} ^ {*} $
Ou $ S_ {11} = -S_ {12} \: \: ou \: \: S_ {12} = -S_ {11} $......... Equation 9
En les utilisant dans l'équation 3,
Depuis, $ S_ {13} \ neq 0, S_ {11} ^ {*} + S_ {12} ^ {*} = 0, \: ou \: S_ {11} ^ {*} = -S_ {12} ^ {*} $
$ \ gauche | S_ {11} \ droite | ^ 2 + \ gauche | S_ {11} \ right | ^ 2 + \ frac {1} {2} = 1 \ quad ou \ quad 2 \ left | S_ {11} \ right | ^ 2 = \ frac {1} {2} \ quad ou \ quad S_ {11} = \ frac {1} {2} $..... Equation 10
À partir des équations 8 et 9,
$ S_ {12} = - \ frac {1} {2} $......... Equation 11
$ S_ {22} = \ frac {1} {2} $......... Equation 12
En remplaçant $ S_ {13} $, $ S_ {11} $, $ S_ {12} $ et $ S_ {22} $ des équations 7 et 10, 11 et 12 de l'équation 2,
On a,
$$ \ left [S \ right] = \ begin {bmatrix} \ frac {1} {2} & - \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ - \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & \ frac {1} { \ sqrt {2}} & 0 \ end {bmatrix} $$
Nous savons que $ [b] $ = $ [s] [a] $
$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \ end {bmatrix} = \ begin {bmatrix} \ frac {1} {2} & - \ frac {1} {2} & \ frac {1} { \ sqrt {2}} \\ - \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt { 2}} & \ frac {1} {\ sqrt {2}} & 0 \ end {bmatrix} \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \ end {bmatrix} $$
Il s'agit de la matrice de diffusion pour H-Plane Tee, ce qui explique ses propriétés de diffusion.
Une jonction EH Plane Tee est formée en attachant deux guides d'ondes simples, l'un parallèle et l'autre série, à un guide d'ondes rectangulaire qui a déjà deux ports. Ceci est également appelé commeMagic Tee, ou Hybrid ou 3dB coupler.
Les bras des guides d'ondes rectangulaires font deux ports appelés collinear ports c'est-à-dire, Port 1 et Port 2, tandis que le Port 3 est appelé comme H-Arm ou Sum port ou Parallel port. Le port 4 est appeléE-Arm ou Difference port ou Series port.
Les détails en coupe de Magic Tee peuvent être compris par la figure suivante.
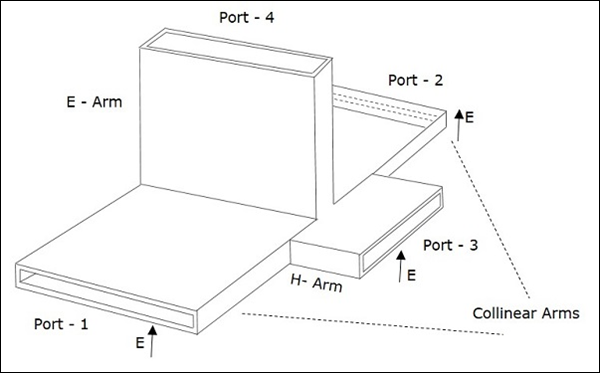
La figure suivante montre la connexion établie par les bras latéraux au guide d'ondes bidirectionnel pour former des ports parallèles et série.
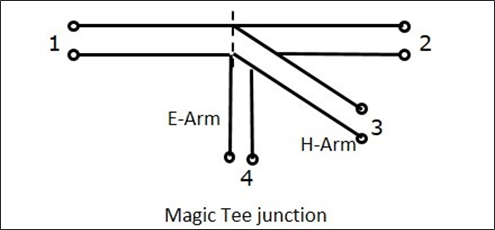
Caractéristiques de EH Plane Tee
Si un signal de phase et d'amplitude égales est envoyé au port 1 et au port 2, alors la sortie sur le port 4 est zéro et la sortie sur le port 3 sera l'additif des deux ports 1 et 2.
Si un signal est envoyé au port 4, (E-arm), la puissance est répartie entre les ports 1 et 2 de manière égale mais en phase opposée, alors qu'il n'y aurait pas de sortie au port 3. Par conséquent, $ S_ {34} $ = 0 .
Si un signal est envoyé au port 3, alors la puissance est répartie entre les ports 1 et 2 de manière égale, alors qu'il n'y aurait pas de sortie au port 4. Par conséquent, $ S_ {43} $ = 0.
Si un signal est fourni à l'un des ports colinéaires, alors il n'y a pas de sortie sur l'autre port colinéaire, car le bras électrique produit un retard de phase et le bras en H produit une avance de phase. Donc, $ S_ {12} $ = $ S_ {21} $ = 0.
Propriétés de EH Plane Tee
Les propriétés de EH Plane Tee peuvent être définies par sa matrice $ \ left [S \ right] _ {4 \ times 4} $.
C'est une matrice 4 × 4 car il y a 4 entrées et 4 sorties possibles.
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} & S_ {14} \\ S_ {21} & S_ {22} & S_ {23} & S_ {24} \\ S_ {31} & S_ {32} & S_ {33} & S_ {34} \\ S_ {41} & S_ {42} & S_ {43} & S_ {44} \ end {bmatrix} $ ........ Equation 1
Comme il a la section H-Plane Tee
$ S_ {23} = S_ {13} $........ Equation 2
Comme il a la section E-Plane Tee
$ S_ {24} = -S_ {14} $........ Equation 3
Le port E-Arm et le port H-Arm sont tellement isolés que l'autre ne fournira pas de sortie, si une entrée est appliquée à l'un d'eux. Par conséquent, cela peut être noté comme
$ S_ {34} = S_ {43} = 0 $........ Equation 4
De la propriété de symétrie, nous avons
$ S_ {ij} = S_ {ji} $
$ S_ {12} = S_ {21}, S_ {13} = S_ {31}, S_ {14} = S_ {41} $
$ S_ {23} = S_ {32}, S_ {24} = S_ {42}, S_ {34} = S_ {43} $........ Equation 5
Si les ports 3 et 4 sont parfaitement adaptés à la jonction, alors
$ S_ {33} = S_ {44} = 0 $........ Equation 6
En substituant toutes les équations ci-dessus dans l'équation 1, pour obtenir la matrice $ [S] $,
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} & S_ {14} \\ S_ {12} & S_ {22} & S_ {13} & -S_ {14 } \\ S_ {13} & S_ {13} & 0 & 0 \\ S_ {14} & -S_ {14} & 0 & 0 \ end {bmatrix} $........ Equation 7
Depuis la propriété Unitary, $ [S] [S] ^ \ ast = [I] $
$ \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} & S_ {14} \\ S_ {12} & S_ {22} & S_ {13} & -S_ {14} \\ S_ {13} & S_ {13} & 0 & 0 \\ S_ {14} & -S_ {14} & 0 & 0 \ end {bmatrix} \ begin {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} & S_ {13} ^ {*} & S_ {14} ^ {*} \\ S_ {12} ^ {*} & S_ {22} ^ {*} & S_ {13} ^ {*} & -S_ {14} ^ {*} \\ S_ {13} & S_ {13} & 0 & 0 \\ S_ {14} & -S_ {14} & 0 & 0 \ end {bmatrix} $
$ = \ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $
$ R_1C_1: \ gauche | S_ {11} \ droite | ^ 2 + \ gauche | S_ {12} \ droite | ^ 2 + \ gauche | S_ {13} \ droite | ^ 2 = 1 + \ gauche | S_ {14} \ droite | ^ 2 = 1 $......... Equation 8
$ R_2C_2: \ gauche | S_ {12} \ droite | ^ 2 + \ gauche | S_ {22} \ droite | ^ 2 + \ gauche | S_ {13} \ droite | ^ 2 = 1 + \ gauche | S_ {14} \ droite | ^ 2 = 1 $......... Equation 9
$ R_3C_3: \ gauche | S_ {13} \ droite | ^ 2 + \ gauche | S_ {13} \ droite | ^ 2 = 1 $......... Equation 10
$ R_4C_4: \ gauche | S_ {14} \ droite | ^ 2 + \ gauche | S_ {14} \ droite | ^ 2 = 1 $......... Equation 11
À partir des équations 10 et 11, nous obtenons
$ S_ {13} = \ frac {1} {\ sqrt {2}} $........ Equation 12
$ S_ {14} = \ frac {1} {\ sqrt {2}} $........ Equation 13
En comparant les équations 8 et 9, nous avons
$ S_ {11} = S_ {22} $ ......... Equation 14
En utilisant ces valeurs des équations 12 et 13, nous obtenons
$ \ gauche | S_ {11} \ droite | ^ 2 + \ gauche | S_ {12} \ right | ^ 2 + \ frac {1} {2} + \ frac {1} {2} = 1 $
$ \ gauche | S_ {11} \ droite | ^ 2 + \ gauche | S_ {12} \ droite | ^ 2 = 0 $
$ S_ {11} = S_ {22} = 0 $ ......... Equation 15
À partir de l'équation 9, nous obtenons $ S_ {22} = 0 $ ......... Equation 16
Nous comprenons maintenant que les ports 1 et 2 sont parfaitement adaptés à la jonction. Comme il s'agit d'une jonction à 4 ports, chaque fois que deux ports sont parfaitement adaptés, les deux autres ports sont également parfaitement adaptés à la jonction.
La jonction où les quatre ports sont parfaitement assortis s'appelle Magic Tee Junction.
En substituant les équations de 12 à 16, dans la matrice $ [S] $ de l'équation 7, on obtient la matrice de diffusion de Magic Tee comme
$$ [S] = \ begin {bmatrix} 0 & 0 & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ 0 & 0 & \ frac {1} {2} & - \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & \ frac {1} {\ sqrt {2}} & 0 & 0 \\ \ frac {1} {\ sqrt {2}} & - \ frac {1} {\ sqrt {2}} & 0 & 0 \ end {bmatrix} $$
Nous savons déjà que, $ [b] $ = $ [S] [a] $
En réécrivant ce qui précède, nous obtenons
$$ \ begin {vmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \ end {vmatrix} = \ begin {bmatrix} 0 & 0 & \ frac {1} {2} & \ frac {1} {\ sqrt {2} } \\ 0 & 0 & \ frac {1} {2} & - \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & \ frac {1} {\ sqrt {2}} & 0 & 0 \\ \ frac {1} {\ sqrt {2}} & - \ frac {1} {\ sqrt {2}} & 0 & 0 \ end {bmatrix} \ begin {vmatrix} a_1 \ \ a_2 \\ a_3 \\ a_4 \ end {vmatrix} $$
Applications de EH Plane Tee
Certaines des applications les plus courantes de EH Plane Tee sont les suivantes:
La jonction EH Plane est utilisée pour mesurer l'impédance - Un détecteur nul est connecté au port E-Arm tandis que la source hyperfréquence est connectée au port H-Arm. Les ports colinéaires avec ces ports forment un pont et la mesure de l'impédance est effectuée en équilibrant le pont.
EH Plane Tee est utilisé comme duplexeur - Un duplexeur est un circuit qui fonctionne à la fois comme émetteur et comme récepteur, en utilisant une seule antenne pour les deux fins. Les ports 1 et 2 sont utilisés comme récepteur et émetteur là où ils sont isolés et n'interféreront donc pas. L'antenne est connectée au port E-Arm. Une charge adaptée est connectée au port H-Arm, qui ne fournit aucune réflexion. Or, il existe une transmission ou une réception sans aucun problème.
EH Plane Tee est utilisé comme mélangeur - le port E-Arm est connecté à l'antenne et le port H-Arm est connecté à l'oscillateur local. Le port 2 a une charge adaptée qui n'a pas de réflexions et le port 1 a le circuit mélangeur, qui obtient la moitié de la puissance du signal et la moitié de la puissance de l'oscillateur pour produire la fréquence IF.
En plus des applications ci-dessus, une jonction EH Plane Tee est également utilisée comme pont micro-ondes, discriminateur micro-ondes, etc.
Ce dispositif hyperfréquence est utilisé lorsqu'il est nécessaire de combiner deux signaux sans différence de phase et d'éviter les signaux avec une différence de chemin.
Une jonction normale à trois ports en T est prise et un quatrième port y est ajouté, pour en faire une jonction de course de rat. Tous ces ports sont connectés sous forme d'anneau angulaire à intervalles égaux à l'aide de jonctions série ou parallèles.
La circonférence moyenne de la course totale est de 1,5λ et chacun des quatre orifices est séparé par une distance de λ / 4. La figure suivante montre l'image d'une jonction Rat-race.
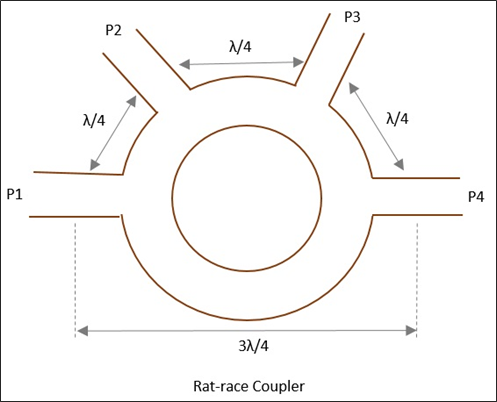
Considérons quelques cas pour comprendre le fonctionnement d'une jonction Rat-race.
Cas 1
Si l'alimentation d'entrée est appliquée au port 1, elle est également divisée en deux ports, mais dans le sens horaire pour le port 2 et dans le sens antihoraire pour le port 4. Le port 3 n'a absolument aucune sortie.
La raison étant, aux ports 2 et 4, les puissances se combinent en phase, alors qu'au port 3, l'annulation se produit en raison de la différence de trajet λ / 2.
Cas 2
Si la puissance d'entrée est appliquée au port 3, la puissance est également répartie entre le port 2 et le port 4. Mais il n'y aura pas de sortie sur le port 1.
Cas 3
Si deux signaux inégaux sont appliqués au port 1 lui-même, alors la sortie sera proportionnelle à la somme des deux signaux d'entrée, qui est divisée entre les ports 2 et 4. Maintenant, au port 3, la sortie différentielle apparaît.
La matrice de dispersion pour la jonction Rat-race est représentée par
$$ [S] = \ begin {bmatrix} 0 & S_ {12} & 0 & S_ {14} \\ S_ {21} & 0 & S_ {23} & 0 \\ 0 & S_ {32} & 0 & S_ {34} \ \ S_ {41} & 0 & S_ {43} & 0 \ end {bmatrix} $$
Applications
La jonction de race de rat est utilisée pour combiner deux signaux et diviser un signal en deux moitiés.
UNE Directional couplerest un appareil qui échantillonne une petite quantité de puissance micro-ondes à des fins de mesure. Les mesures de puissance incluent la puissance incidente, la puissance réfléchie, les valeurs VSWR, etc.
Le coupleur directionnel est une jonction de guide d'ondes à 4 ports composée d'un guide d'ondes principal principal et d'un guide d'ondes auxiliaire secondaire. La figure suivante montre l'image d'un coupleur directionnel.
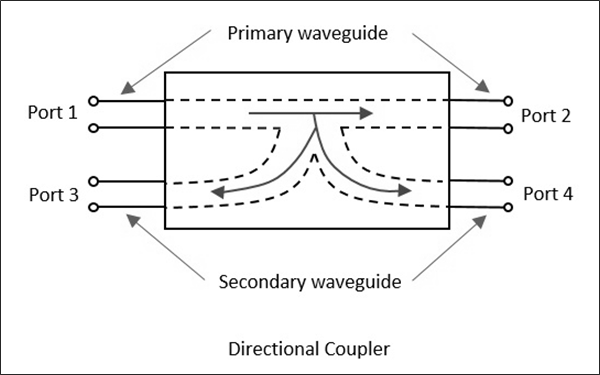
Le coupleur directionnel est utilisé pour coupler la puissance hyperfréquence qui peut être unidirectionnelle ou bidirectionnelle.
Propriétés des coupleurs directionnels
Les propriétés d'un coupleur directionnel idéal sont les suivantes.
Toutes les terminaisons sont adaptées aux ports.
Lorsque l'alimentation se déplace du port 1 au port 2, une partie de celle-ci est couplée au port 4 mais pas au port 3.
Comme il s'agit également d'un coupleur bidirectionnel, lorsque la puissance passe du port 2 au port 1, une partie de celui-ci est couplée au port 3 mais pas au port 4.
Si l'alimentation est incidente via le port 3, une partie de celle-ci est couplée au port 2, mais pas au port 1.
Si l'alimentation est incidente via le port 4, une partie de celle-ci est couplée au port 1, mais pas au port 2.
Les ports 1 et 3 sont découplés, tout comme les ports 2 et 4.
Idéalement, la sortie du port 3 devrait être nulle. Cependant, pratiquement, une petite quantité de puissance appeléeback power est observée au port 3. La figure suivante indique le flux de puissance dans un coupleur directionnel.
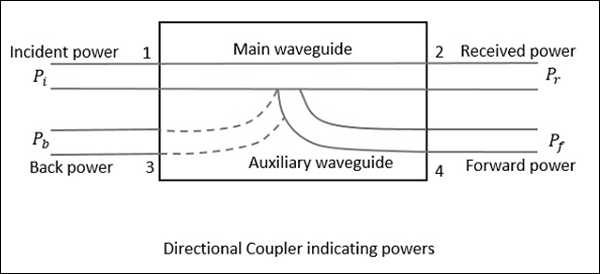
Où
$ P_i $ = Puissance incidente au port 1
$ P_r $ = Puissance reçue au port 2
$ P_f $ = Puissance couplée vers l'avant au port 4
$ P_b $ = alimentation de retour au port 3
Voici les paramètres utilisés pour définir les performances d'un coupleur directionnel.
Facteur de couplage (C)
Le facteur de couplage d'un coupleur directionnel est le rapport entre la puissance incidente et la puissance directe, mesurée en dB.
$$ C = 10 \: log_ {10} \ frac {P_i} {P_f} dB $$
Directivité (D)
La directivité d'un coupleur directionnel est le rapport entre la puissance directe et la puissance arrière, mesurée en dB.
$$ D = 10 \: log_ {10} \ frac {P_f} {P_b} dB $$
Isolement
Il définit les propriétés directive d'un coupleur directionnel. C'est le rapport entre la puissance incidente et la puissance de retour, mesurée en dB.
$$ I = 10 \: log_ {10} \ frac {P_i} {P_b} dB $$
Isolation in dB = Coupling factor + Directivity
Coupleur directionnel à deux trous
Il s'agit d'un coupleur directionnel avec les mêmes guides d'ondes principaux et auxiliaires, mais avec deux petits trous communs entre eux. Ces trous sont distants de $ {\ lambda_g} / {4} $ où λg est la longueur d'onde guide. La figure suivante montre l'image d'un coupleur directionnel à deux trous.
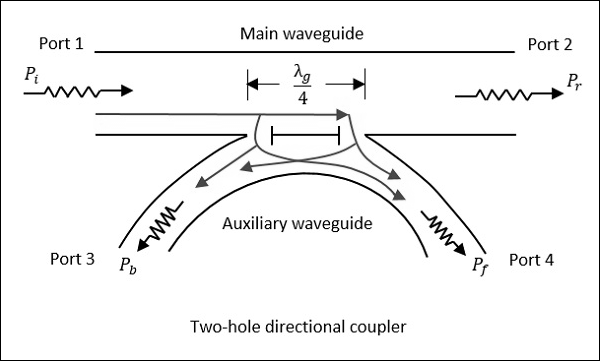
Un coupleur directionnel à deux trous est conçu pour répondre à l'exigence idéale du coupleur directionnel, qui est d'éviter la puissance de retour. Une partie de la puissance en voyageant entre le port 1 et le port 2 s'échappe par les trous 1 et 2.
L'ampleur de la puissance dépend des dimensions des trous. Cette puissance de fuite aux deux trous est en phase au trou 2, additionnant la puissance contribuant à la puissance directePf. Cependant, il est déphasé au trou 1, s'annulant mutuellement et empêchant le retour de puissance de se produire.
Par conséquent, la directivité d'un coupleur directionnel s'améliore.
Joints de guide d'ondes
Comme un système de guide d'ondes ne peut pas toujours être construit en une seule pièce, il est parfois nécessaire de joindre différents guides d'ondes. Cette jonction doit être soigneusement réalisée pour éviter des problèmes tels que - Effets de réflexion, création d'ondes stationnaires et augmentation de l'atténuation, etc.
Les joints du guide d'ondes, en plus d'éviter les irrégularités, doivent également prendre en compte les modèles de champ E et H en ne les affectant pas. Il existe de nombreux types de joints de guide d'ondes tels que les brides boulonnées, les joints de bride, les joints de starter, etc.
Pour la génération et l'amplification des micro-ondes, il existe un besoin de certains tubes spéciaux appelés comme Microwave tubes. De tous,Klystron est une question importante.
Les éléments essentiels de Klystron sont les faisceaux d'électrons et les résonateurs à cavité. Des faisceaux d'électrons sont produits à partir d'une source et les klystrons de cavité sont utilisés pour amplifier les signaux. Un collecteur est présent à l'extrémité pour collecter les électrons. L'ensemble de la configuration est comme indiqué dans la figure suivante.
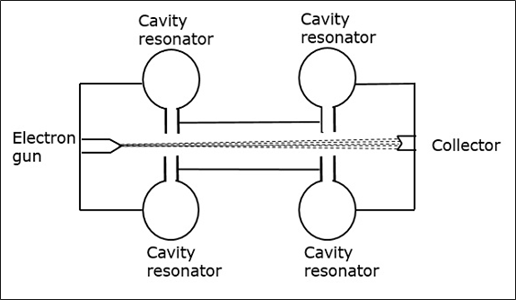
Les électrons émis par la cathode sont accélérés vers le premier résonateur. Le collecteur à la fin est au même potentiel que le résonateur. Par conséquent, les électrons ont généralement une vitesse constante dans l'espace entre les résonateurs de la cavité.
Initialement, le premier résonateur à cavité est alimenté par un faible signal haute fréquence, qui doit être amplifié. Le signal déclenchera un champ électromagnétique à l'intérieur de la cavité. Ce signal est passé à travers un câble coaxial comme indiqué dans la figure suivante.

En raison de ce champ, les électrons qui traversent le résonateur de la cavité sont modulés. En arrivant au deuxième résonateur, les électrons sont induits avec un autre EMF à la même fréquence. Ce champ est suffisamment puissant pour extraire un signal important de la seconde cavité.
Résonateur à cavité
Essayons d'abord de comprendre les détails de construction et le fonctionnement d'un résonateur à cavité. La figure suivante indique le résonateur à cavité.
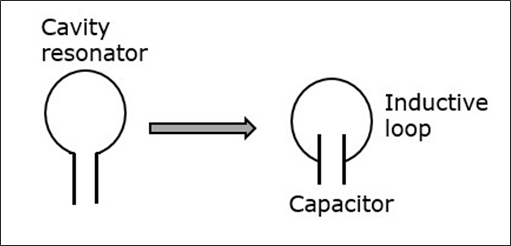
Un simple circuit résonant composé d'un condensateur et d'une boucle inductive peut être comparé à ce résonateur à cavité. Un conducteur a des électrons libres. Si une charge est appliquée au condensateur pour le charger à une tension de cette polarité, de nombreux électrons sont retirés de la plaque supérieure et introduits dans la plaque inférieure.
La plaque qui a le plus de dépôt d'électrons sera la cathode et la plaque qui a le moins d'électrons devient l'anode. La figure suivante montre le dépôt de charge sur le condensateur.
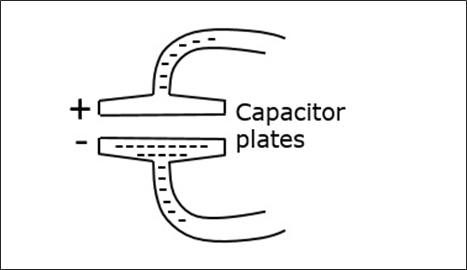
Les lignes de champ électrique sont dirigées de la charge positive vers le négatif. Si le condensateur est chargé avec une polarité inversée, la direction du champ est également inversée. Le déplacement des électrons dans le tube, constitue un courant alternatif. Ce courant alternatif donne naissance à un champ magnétique alternatif, qui est déphasé avec le champ électrique du condensateur.
Lorsque le champ magnétique est à son intensité maximale, le champ électrique est nul et après un certain temps, le champ électrique devient maximal alors que le champ magnétique est à zéro. Cet échange de force se produit pendant un cycle.
Résonateur fermé
Plus la valeur du condensateur et l'inductivité de la boucle sont petites, plus l'oscillation ou la fréquence de résonance sera élevée. Comme l'inductance de la boucle est très petite, une fréquence élevée peut être obtenue.
Pour produire un signal de fréquence plus élevée, l'inductance peut être encore réduite en plaçant davantage de boucles inductives en parallèle, comme illustré sur la figure suivante. Il en résulte la formation d'un résonateur fermé ayant des fréquences très élevées.
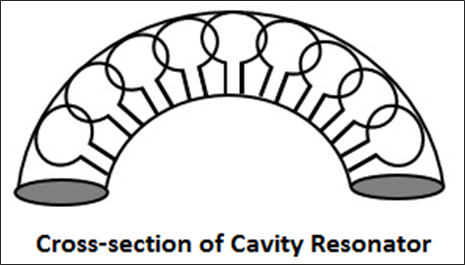
Dans un résonateur fermé, les champs électriques et magnétiques sont confinés à l'intérieur de la cavité. Le premier résonateur de la cavité est excité par le signal externe à amplifier. Ce signal doit avoir une fréquence à laquelle la cavité peut résonner. Le courant dans ce câble coaxial établit un champ magnétique, par lequel un champ électrique provient.
Fonctionnement de Klystron
Pour comprendre la modulation du faisceau d'électrons, entrant dans la première cavité, considérons le champ électrique. Le champ électrique sur le résonateur continue de changer sa direction du champ induit. En fonction de cela, les électrons sortant du canon à électrons contrôlent leur rythme.
Comme les électrons sont chargés négativement, ils sont accélérés s'ils sont déplacés dans le sens opposé à la direction du champ électrique. De plus, si les électrons se déplacent dans la même direction que le champ électrique, ils sont décélérés. Ce champ électrique ne cesse de changer, donc les électrons sont accélérés et décélérés en fonction du changement du champ. La figure suivante indique le flux d'électrons lorsque le champ est dans la direction opposée.
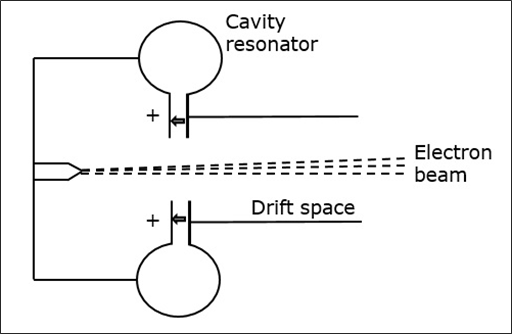
En se déplaçant, ces électrons pénètrent dans l'espace libre de champ appelé drift spaceentre les résonateurs avec des vitesses variables, qui créent des paquets d'électrons. Ces grappes sont créées en raison de la variation de la vitesse de déplacement.
Ces paquets entrent dans le deuxième résonateur, avec une fréquence correspondant à la fréquence à laquelle le premier résonateur oscille. Comme tous les résonateurs de la cavité sont identiques, le mouvement des électrons fait osciller le second résonateur. La figure suivante montre la formation de paquets d'électrons.
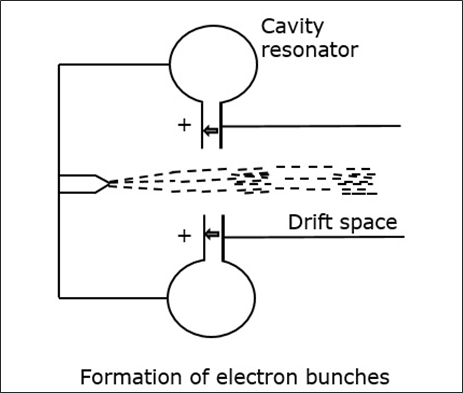
Le champ magnétique induit dans le second résonateur induit du courant dans le câble coaxial, déclenchant le signal de sortie. L'énergie cinétique des électrons dans la seconde cavité est presque égale à celle de la première cavité et donc aucune énergie n'est prélevée dans la cavité.
Les électrons en traversant la seconde cavité, peu d'entre eux sont accélérés tandis que les paquets d'électrons sont décélérés. Par conséquent, toute l'énergie cinétique est convertie en énergie électromagnétique pour produire le signal de sortie.
L'amplification d'un tel Klystron à deux cavités est faible et donc des Klystrons à plusieurs cavités sont utilisés.
La figure suivante illustre un exemple d'amplificateur Klystron à cavités multiples.
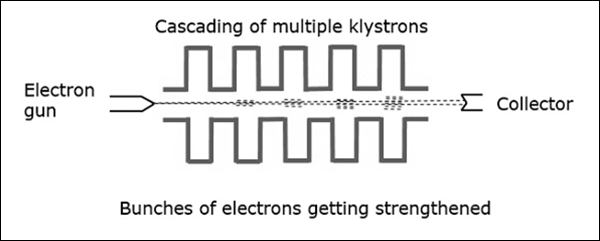
Avec le signal appliqué dans la première cavité, nous obtenons des grappes faibles dans la deuxième cavité. Celles-ci créeront un champ dans la troisième cavité, ce qui produira des grappes plus concentrées et ainsi de suite. Par conséquent, l'amplification est plus grande.
Ce générateur de micro-ondes, est un Klystron qui fonctionne sur les réflexions et les oscillations dans une seule cavité, qui a une fréquence variable.
Reflex Klystron se compose d'un canon à électrons, d'un filament cathodique, d'une cavité anodique et d'une électrode au potentiel cathodique. Il fournit une faible puissance et un faible rendement.
Construction du Reflex Klystron
Le canon à électrons émet le faisceau d'électrons, qui traverse l'espace dans la cavité anodique. Ces électrons se déplacent vers l'électrode Repeller, qui est à un potentiel négatif élevé. En raison du champ négatif élevé, les électrons se repoussent vers la cavité anodique. Dans leur voyage de retour, les électrons donnent plus d'énergie à l'écart et ces oscillations se prolongent. Les détails de construction de ce klystron réflexe sont indiqués dans la figure suivante.
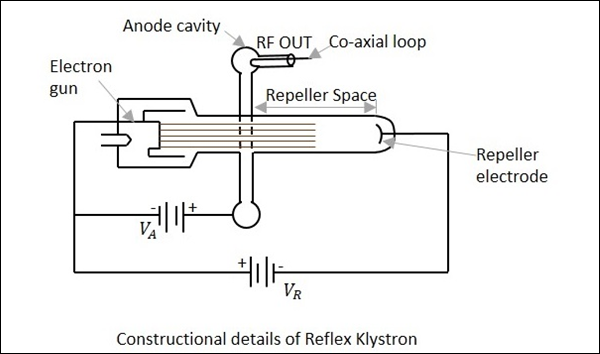
On suppose que des oscillations existent déjà dans le tube et qu'elles sont entretenues par son fonctionnement. Les électrons en traversant la cavité anodique gagnent une certaine vitesse.
Fonctionnement du Reflex Klystron
Le fonctionnement de Reflex Klystron est compris par certaines hypothèses. Le faisceau d'électrons est accéléré vers la cavité anodique.
Supposons qu'un électron de référence ertraverse la cavité anodique mais n'a pas de vitesse supplémentaire et il repousse après avoir atteint l'électrode Repeller, avec la même vitesse. Un autre électron, disonsee qui a commencé plus tôt que cet électron de référence, atteint en premier le Repeller, mais revient lentement, atteignant en même temps que l'électron de référence.
Nous avons un autre électron, l'électron tardif el, qui commence plus tard que les deux er et eecependant, il se déplace avec une plus grande vitesse en revenant en arrière, atteignant en même temps que er et ee.
Or, ces trois électrons, à savoir er, ee et el atteindre le fossé en même temps, formant un electron bunch. Ce temps de trajet est appelétransit time, qui devrait avoir une valeur optimale. La figure suivante illustre cela.

La cavité anodique accélère les électrons en allant et gagne leur énergie en les retardant lors du retour. Lorsque la tension d'intervalle est au maximum positif, cela permet au maximum d'électrons négatifs de retarder.
Le temps de transit optimal est représenté par
$$ T = n + \ frac {3} {4} \ quad où \: n \: est \: an \: entier $$
Ce temps de transit dépend du répulsif et des tensions d'anode.
Applications de Reflex Klystron
Reflex Klystron est utilisé dans les applications où une fréquence variable est souhaitable, telles que -
- Récepteurs radio
- Liaisons micro-ondes portables
- Amplificateurs paramétriques
- Oscillateurs locaux de récepteurs micro-ondes
- En tant que source de signal où une fréquence variable est souhaitable dans les générateurs de micro-ondes.
Les tubes à ondes progressives sont des appareils à micro-ondes à large bande qui n'ont pas de résonateurs à cavité comme les Klystrons. L'amplification se fait par l'interaction prolongée entre un faisceau d'électrons et un champ de radiofréquence (RF).
Construction d'un tube à ondes mobiles
Le tube à ondes progressives est une structure cylindrique qui contient un canon à électrons provenant d'un tube cathodique. Il a des plaques d'anode, une hélice et un collecteur. L'entrée RF est envoyée à une extrémité de l'hélice et la sortie est tirée de l'autre extrémité de l'hélice.
Un canon à électrons focalise un faisceau d'électrons avec la vitesse de la lumière. Un champ magnétique guide le faisceau pour se concentrer, sans diffusion. Le champ RF se propage également avec la vitesse de la lumière qui est retardée par une hélice. Helix agit comme une structure à ondes lentes. Le champ RF appliqué, propagé en hélice, produit un champ électrique au centre de l'hélice.
Le champ électrique résultant dû au signal RF appliqué se déplace avec la vitesse de la lumière multipliée par le rapport du pas de l'hélice à la circonférence de l'hélice. La vitesse du faisceau d'électrons, voyageant à travers l'hélice, induit de l'énergie aux ondes RF sur l'hélice.
La figure suivante explique les caractéristiques de construction d'un tube à ondes progressives.

Ainsi, la sortie amplifiée est obtenue en sortie de TWT. La vitesse de phase axiale $ V_p $ est représentée par
$$ V_p = V_c \ left ({Pitch} / {2 \ pi r} \ right) $$
Où rest le rayon de l'hélice. Comme l'hélice fournit le moins de changement dans la vitesse de phase $ V_p $, elle est préférée aux autres structures à ondes lentes pour TWT. Dans TWT, le canon à électrons focalise le faisceau d'électrons, dans l'espace entre les plaques anodiques, sur l'hélice, qui est ensuite collectée au niveau du collecteur. La figure suivante explique les dispositions des électrodes dans un tube à ondes progressives.
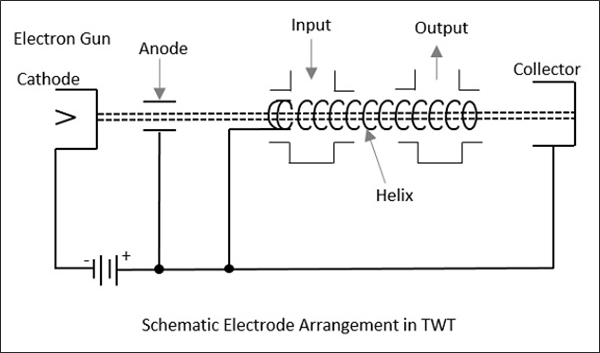
Fonctionnement du tube à ondes progressives
Les plaques anodiques, lorsqu'elles sont à potentiel nul, ce qui signifie que lorsque le champ électrique axial est à un nœud, la vitesse du faisceau d'électrons reste inchangée. Lorsque l'onde sur le champ électrique axial est à l'antinode positif, l'électron du faisceau d'électrons se déplace dans la direction opposée. Cet électron en accéléré, tente de rattraper l'électron tardif, qui rencontre le nœud du champ axial RF.
Au point où le champ axial RF est à l'antinode négatif, l'électron référencé plus tôt, tente de dépasser en raison de l'effet de champ négatif. Les électrons reçoivent une vitesse modulée. En conséquence cumulative, une seconde onde est induite dans l'hélice. La sortie devient plus grande que l'entrée et entraîne une amplification.
Applications du tube à ondes progressives
Il existe de nombreuses applications d'un tube à ondes progressives.
TWT est utilisé dans les récepteurs micro-ondes comme amplificateur RF à faible bruit.
Les TWT sont également utilisés dans les liaisons de communication à large bande et les câbles coaxiaux comme amplificateurs répéteurs ou amplificateurs intermédiaires pour amplifier les signaux faibles.
Les TWT ont une longue durée de vie, grâce à laquelle ils sont utilisés comme tubes de sortie de puissance dans les satellites de communication.
Les TWT haute puissance à onde continue sont utilisés dans les liaisons Troposcatter, en raison de leur grande puissance et de leur large bande passante, pour se disperser sur de grandes distances.
Les TWT sont utilisés dans les radars pulsés haute puissance et les radars au sol.
Contrairement aux tubes discutés jusqu'à présent, les magnétrons sont les tubes à champ croisé dans lesquels les champs électrique et magnétique se croisent, c'est-à-dire perpendiculaires l'un à l'autre. Dans TWT, il a été observé que les électrons, lorsqu'ils sont amenés à interagir avec RF, pendant une durée plus longue, que dans Klystron, entraînaient une efficacité plus élevée. La même technique est suivie dans les magnétrons.
Types de magnétrons
Il existe trois principaux types de magnétrons.
Type de résistance négative
- La résistance négative entre deux segments d'anode est utilisée.
- Ils ont une faible efficacité.
- Ils sont utilisés aux basses fréquences (<500 MHz).
Magnétrons de fréquence cyclotron
Le synchronisme entre le composant électrique et les électrons oscillants est considéré.
Utile pour les fréquences supérieures à 100 MHz.
Type d'onde ou de cavité de déplacement
L'interaction entre les électrons et le champ électromagnétique tournant est prise en compte.
Des oscillations de puissance de crête élevées sont fournies.
Utile dans les applications radar.
Magnétron à cavité
Le magnétron est appelé magnétron à cavité car l'anode est transformée en cavités résonnantes et un aimant permanent est utilisé pour produire un champ magnétique puissant, où l'action de ces deux éléments fait fonctionner l'appareil.
Construction du magnétron à cavité
Une cathode cylindrique épaisse est présente au centre et un bloc cylindrique de cuivre, est fixé axialement, qui agit comme une anode. Ce bloc anodique est constitué d'un certain nombre de fentes qui agissent comme des cavités anodiques résonnantes.
L'espace présent entre l'anode et la cathode est appelé Interaction space. Le champ électrique est présent radialement tandis que le champ magnétique est présent axialement dans le magnétron de la cavité. Ce champ magnétique est produit par un aimant permanent, qui est placé de telle sorte que les lignes magnétiques soient parallèles à la cathode et perpendiculaires au champ électrique présent entre l'anode et la cathode.
Les figures suivantes montrent les détails de construction d'un magnétron à cavité et les lignes magnétiques de flux présentes, axialement.

Ce magnétron à cavité comporte 8 cavités étroitement couplées les unes aux autres. Un magnétron à N cavités a des modes de fonctionnement $ N $. Ces opérations dépendent de la fréquence et de la phase des oscillations. Le déphasage total autour de l'anneau de ces résonateurs à cavité devrait être $ 2n \ pi $ où $ n $ est un entier.
Si $ \ phi_v $ représente le changement de phase relatif du champ électrique alternatif à travers les cavités adjacentes, alors
$$ \ phi_v = \ frac {2 \ pi n} {N} $$
Où $ n = 0, \: \ pm1, \: \ pm2, \: \ pm \: (\ frac {N} {2} -1), \: \ pm \ frac {N} {2} $
Ce qui signifie que $ \ frac {N} {2} $ mode de résonance peut exister si $ N $ est un nombre pair.
Si,
$$ n = \ frac {N} {2} \ quad puis \ quad \ phi_v = \ pi $$
Ce mode de résonance est appelé $ \ pi-mode $.
$$ n = 0 \ quad puis \ quad \ phi_v = 0 $$
Ceci est appelé comme le Zero mode, car il n'y aura pas de champ électrique RF entre l'anode et la cathode. Ceci est également appelé commeFringing Field et ce mode n'est pas utilisé dans les magnétrons.
Fonctionnement du magnétron à cavité
Lorsque le Cavity Klystron est en fonctionnement, nous avons différents cas à considérer. Examinons-les en détail.
Case 1
Si le champ magnétique est absent, c'est-à-dire B = 0, alors le comportement des électrons peut être observé sur la figure suivante. Considérant un exemple, où l'électrona va directement à l'anode sous la force électrique radiale.
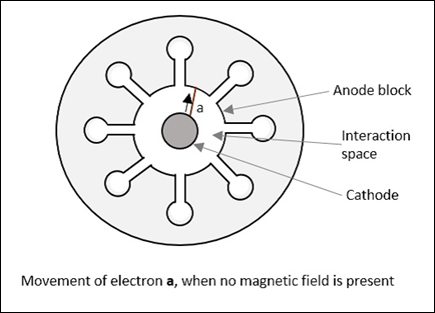
Case 2
En cas d'augmentation du champ magnétique, une force latérale agit sur les électrons. Ceci peut être observé dans la figure suivante, en considérant l'électronb qui emprunte une trajectoire courbe, tandis que les deux forces agissent dessus.

Le rayon de ce chemin est calculé comme
$$ R = \ frac {mv} {eB} $$
Elle varie proportionnellement à la vitesse de l'électron et elle est inversement proportionnelle à l'intensité du champ magnétique.
Case 3
Si le champ magnétique B est encore augmenté, l'électron suit un chemin tel que l'électron c, effleurant simplement la surface de l'anode et rendant le courant d'anode nul. Ceci est appelé comme "Critical magnetic field"$ (B_c) $, qui est le champ magnétique de coupure. Reportez-vous à la figure suivante pour une meilleure compréhension.
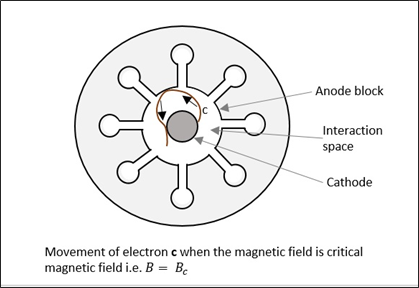
Case 4
Si le champ magnétique est rendu supérieur au champ critique,
$$ B> B_c $$
Ensuite, les électrons suivent un chemin comme électron d, où l'électron retourne à la cathode, sans aller à l'anode. Ce qui provoque "back heating"de la cathode. Reportez-vous à la figure suivante.
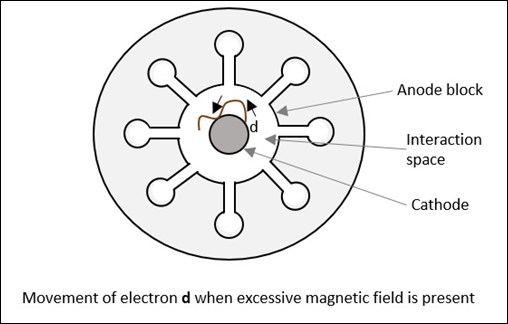
Ceci est réalisé en coupant l'alimentation électrique une fois que l'oscillation commence. Si cela se poursuit, l'efficacité d'émission de la cathode est affectée.
Fonctionnement du magnétron à cavité avec champ RF actif
Nous avons discuté jusqu'à présent du fonctionnement du magnétron à cavité où le champ RF est absent dans les cavités du magnétron (cas statique). Parlons maintenant de son fonctionnement lorsque nous avons un champ RF actif.
Comme dans TWT, supposons que des oscillations RF initiales soient présentes, dues à un bruit transitoire. Les oscillations sont entretenues par le fonctionnement de l'appareil. Il existe trois types d'électrons émis dans ce processus, dont les actions sont comprises comme des électronsa, b et c, dans trois cas différents.
Case 1
Quand des oscillations sont présentes, un électron a, ralentit le transfert d'énergie pour osciller. De tels électrons qui transfèrent leur énergie aux oscillations sont appelésfavored electrons. Ces électrons sont responsables debunching effect.
Case 2
Dans ce cas, un autre électron, disons b, prend l'énergie des oscillations et augmente sa vitesse. Au fur et à mesure que cela est fait,
- Il se plie plus brusquement.
- Il passe peu de temps dans l'espace d'interaction.
- Il retourne à la cathode.
Ces électrons sont appelés comme unfavored electrons. Ils ne participent pas à l'effet de regroupement. En outre, ces électrons sont nocifs car ils provoquent un «contre-échauffement».
Case 3
Dans ce cas, électron c, qui est émis un peu plus tard, se déplace plus vite. Il essaie de rattraper l'électrona. Le prochain électron émisd, essaie de marcher avec a. En conséquence, les électrons favorisa, c et dforment des paquets d'électrons ou des nuages d'électrons. Il a appelé comme "effet de focalisation de phase".
L'ensemble de ce processus est mieux compris en regardant la figure suivante.

La figure A montre les mouvements d'électrons dans différents cas tandis que la figure B montre les nuages d'électrons formés. Ces nuages d'électrons se produisent pendant le fonctionnement de l'appareil. Les charges présentes sur la surface interne de ces segments d'anode, suivent les oscillations dans les cavités. Cela crée un champ électrique tournant dans le sens des aiguilles d'une montre, qui peut être réellement vu lors d'une expérience pratique.
Pendant que le champ électrique tourne, les lignes de flux magnétique se forment parallèlement à la cathode, sous l'effet combiné de laquelle, les paquets d'électrons sont formés à quatre rayons, dirigés à intervalles réguliers, vers le segment d'anode positif le plus proche, selon des trajectoires en spirale.
Parmi les appareils de mesure hyperfréquences, une configuration de banc hyperfréquence, qui se compose d'appareils hyperfréquences, occupe une place de choix. L'ensemble de cette configuration, avec quelques alternances, est capable de mesurer de nombreuses valeurs telles que la longueur d'onde guide, la longueur d'onde de l'espace libre, la longueur d'onde de coupure, l'impédance, la fréquence, le VSWR, les caractéristiques Klystron, les caractéristiques de la diode Gunn, les mesures de puissance, etc.
La puissance produite par les micro-ondes, pour déterminer la puissance, est généralement d'une faible valeur. Ils varient avec la position dans une ligne de transmission. Il devrait y avoir un équipement pour mesurer la puissance micro-ondes, qui en général sera une configuration de banc micro-ondes.
Configuration générale de la mesure du banc à micro-ondes
Cette configuration est une combinaison de différentes parties qui peuvent être observées en détail. La figure suivante explique clairement la configuration.

Générateur de signal
Comme son nom l'indique, il génère un signal micro-onde, de l'ordre de quelques milliwatts. Cela utilise la technique de modulation de vitesse pour transférer le faisceau d'onde continue en puissance milliwatt.
Un oscillateur à diode Gunn ou un tube Reflex Klystron pourrait être un exemple pour ce générateur de signal hyperfréquence.
Atténuateur de précision
C'est l'atténuateur qui sélectionne la fréquence souhaitée et limite la sortie autour de 0 à 50db. Ceci est variable et peut être ajusté en fonction des besoins.
Atténuateur variable
Cet atténuateur règle la quantité d'atténuation. Cela peut être compris comme un ajustement fin des valeurs, où les lectures sont comparées aux valeurs de l'atténuateur de précision.
Isolateur
Cela supprime le signal qui n'est pas nécessaire pour atteindre le support du détecteur. L'isolateur permet au signal de passer à travers le guide d'ondes dans une seule direction.
Fréquencemètre
C'est l'appareil qui mesure la fréquence du signal. Avec ce fréquencemètre, le signal peut être ajusté à sa fréquence de résonance. Il permet également de coupler le signal au guide d'ondes.
Détecteur de cristal
Une sonde de détecteur de cristal et un support de détecteur de cristal sont indiqués sur la figure ci-dessus, où le détecteur est connecté via une sonde au support. Ceci est utilisé pour démoduler les signaux.
Indicateur d'onde stationnaire
Le voltmètre à ondes stationnaires fournit la lecture du rapport des ondes stationnaires en dB. Le guide d'ondes est fendu par un espace pour ajuster les cycles d'horloge du signal. Les signaux transmis par guide d'ondes sont acheminés via un câble BNC vers VSWR ou CRO pour mesurer ses caractéristiques.
Un banc à micro-ondes mis en place dans une application en temps réel ressemblerait à ceci:

Maintenant, jetons un coup d'œil à la partie importante de ce banc à micro-ondes, la ligne à fentes.
Ligne fendue
Dans une ligne de transmission hyperfréquence ou un guide d'ondes, le champ électromagnétique est considéré comme la somme de l'onde incidente du générateur et de l'onde réfléchie vers le générateur. Les réflexions indiquent une discordance ou une discontinuité. L'amplitude et la phase de l'onde réfléchie dépendent de l'amplitude et de la phase de l'impédance réfléchissante.
Les ondes stationnaires obtenues sont mesurées pour connaître les imperfections de la ligne de transmission, ce qui est nécessaire pour avoir une connaissance de la discordance d'impédance pour une transmission efficace. Cette ligne à fentes aide à mesurer le rapport d'onde stationnaire d'un appareil à micro-ondes.
Construction
La ligne à fentes consiste en une section à fentes d'une ligne de transmission, où la mesure doit être effectuée. Il dispose d'un chariot de sonde mobile, pour permettre à la sonde de se connecter là où c'est nécessaire, et de la possibilité de fixer et de détecter l'instrument.
Dans un guide d'ondes, une fente est pratiquée au centre du grand côté, axialement. Une sonde mobile connectée à un détecteur de cristal est insérée dans la fente du guide d'ondes.
Opération
La sortie du détecteur à cristal est proportionnelle au carré de la tension d'entrée appliquée. La sonde mobile permet une mesure pratique et précise à sa position. Mais, lorsque la sonde est déplacée, sa sortie est proportionnelle au motif d'onde stationnaire, qui se forme à l'intérieur du guide d'ondes. Un atténuateur variable est utilisé ici pour obtenir des résultats précis.
Le VSWR de sortie peut être obtenu par
$$ VSWR = \ sqrt {\ frac {V_ {max}} {V_ {min}}} $$
Où, $ V $ est la tension de sortie.
La figure suivante montre les différentes parties d'une ligne à fentes étiquetées.

Les pièces étiquetées dans la figure ci-dessus indiquent ce qui suit.
- Lanceur - Invite le signal.
- Petite section du guide d'ondes.
- Isolateur - Empêche les réflexions sur la source.
- Atténuateur rotatif variable - Pour des réglages fins.
- Section fendue - Pour mesurer le signal.
- Réglage de la profondeur de la sonde.
- Réglages de réglage - Pour obtenir la précision.
- Détecteur de cristal - Détecte le signal.
- Charge adaptée - Absorbe la puissance produite.
- Court-circuit - Disposition pour être remplacé par une charge.
- Bouton rotatif - Pour régler pendant la mesure.
- Jauge à vernier - Pour des résultats précis.
Afin d'obtenir un signal modulé à basse fréquence sur un oscilloscope, une ligne à fente avec un détecteur accordable est utilisée. Un chariot à lignes à fentes avec un détecteur accordable peut être utilisé pour mesurer ce qui suit.
- VSWR (rapport d'onde stationnaire de tension)
- Modèle d'onde debout
- Impedance
- Coefficient de reflexion
- Perte de retour
- Fréquence du générateur utilisé
Détecteur accordable
Le détecteur accordable est un support de détecteur qui est utilisé pour détecter les signaux micro-ondes modulés en ondes carrées à basse fréquence. La figure suivante donne une idée d'un support de détecteur accordable.
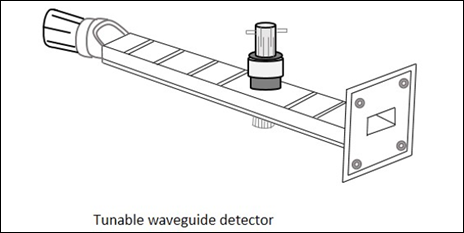
L'image suivante représente l'application pratique de cet appareil. Il est terminé à la fin et a une ouverture à l'autre extrémité tout comme celle ci-dessus.

Pour fournir une correspondance entre le système de transmission hyperfréquence et le support du détecteur, un tronçon réglable est souvent utilisé. Il existe trois types différents de stubs réglables.
- Détecteur de guide d'ondes accordable
- Détecteur coaxial accordable
- Détecteur de sonde réglable
En outre, il existe des stubs fixes comme -
- Sonde réglée à large bande fixe
- Support de détecteur adapté au guide d'ondes fixe
Le support du détecteur est la dernière étape sur un banc micro-ondes qui se termine à la fin.
Dans le domaine de l'ingénierie des micro-ondes, il existe de nombreuses applications, comme déjà indiqué dans le premier chapitre. Par conséquent, en utilisant différentes applications, nous rencontrons souvent le besoin de mesurer différentes valeurs telles que la puissance, l'atténuation, le déphasage, le VSWR, l'impédance, etc. pour une utilisation efficace.
Dans ce chapitre, examinons les différentes techniques de mesure.
Mesure de puissance
La puissance micro-ondes mesurée est la puissance moyenne à n'importe quelle position dans le guide d'ondes. La mesure de puissance peut être de trois types.
-
Mesure de faible puissance (0,01 mW à 10 mW)
Exemple - Technique bolométrique
-
Mesure de puissance moyenne (10 mW à 1 W)
Exemple - Technique du calorimètre
-
Mesure de haute puissance (> 10W)
Exemple - Wattmètre calorimétrique
Examinons-les en détail.
Mesure de faible puissance
La mesure de la puissance micro-ondes autour de 0,01 mW à 10 mW, peut être comprise comme la mesure de faible puissance.
Bolometerest un appareil utilisé pour les mesures de faible puissance micro-ondes. L'élément utilisé dans le bolomètre peut être de coefficient de température positif ou négatif. Par exemple, un barrater a un coefficient de température positif dont la résistance augmente avec l'augmentation de la température. La thermistance a un coefficient de température négatif dont la résistance diminue avec l'augmentation de la température.
N'importe lequel d'entre eux peut être utilisé dans le bolomètre, mais le changement de résistance est proportionnel à la puissance micro-ondes appliquée pour la mesure. Ce bolomètre est utilisé dans un pont des bras comme un seul afin que tout déséquilibre causé, affecte la sortie. Un exemple typique de circuit en pont utilisant un bolomètre est illustré dans la figure suivante.
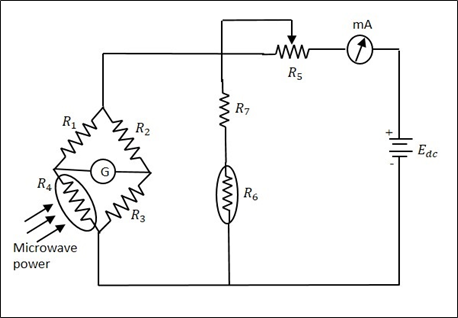
Le millimètre ici, donne la valeur du courant circulant. La batterie est variable, qui est variée pour obtenir l'équilibre, lorsqu'un déséquilibre est provoqué par le comportement du bolomètre. Cet ajustement qui est effectué en tension continue de la batterie est proportionnel à la puissance micro-ondes. La capacité de traitement de puissance de ce circuit est limitée.
Mesure de puissance moyenne
La mesure de la puissance micro-onde autour de 10mW à 1W, peut être comprise comme la mesure de puissance moyenne.
Une charge spéciale est utilisée, qui maintient généralement une certaine valeur de chaleur spécifique. La puissance à mesurer, est appliquée à son entrée qui change proportionnellement la température de sortie de la charge qu'elle maintient déjà. La différence d'élévation de température, spécifie la puissance micro-ondes d'entrée à la charge.
La technique d'équilibrage du pont est utilisée ici pour obtenir la sortie. La méthode de transfert de chaleur est utilisée pour la mesure de la puissance, qui est une technique calorimétrique.
Mesure de haute puissance
La mesure de la puissance micro-ondes autour de 10W à 50KW, peut être comprise comme la mesure d'une puissance élevée.
La puissance hyperfréquence élevée est normalement mesurée par des wattmètres calorimétriques, qui peuvent être de type sec et à débit. Le type sec est nommé ainsi car il utilise un câble coaxial qui est rempli de diélectrique à perte d'hystérésis élevée, tandis que le type d'écoulement est nommé ainsi car il utilise de l'eau ou de l'huile ou un liquide qui est un bon absorbeur de micro-ondes.
Le changement de température du liquide avant et après l'entrée de la charge, est pris pour l'étalonnage des valeurs. Les limites de cette méthode sont comme la détermination du débit, l'étalonnage et l'inertie thermique, etc.
Mesure de l'atténuation
En pratique, les composants et dispositifs hyperfréquences fournissent souvent une certaine atténuation. La quantité d'atténuation offerte peut être mesurée de deux manières. Ce sont: la méthode du rapport de puissance et la méthode de substitution RF.
L'atténuation est le rapport entre la puissance d'entrée et la puissance de sortie et est normalement exprimée en décibels.
$$ Atténuation \: in \: dBs = 10 \: log \ frac {P_ {in}} {P_ {out}} $$
Où $ P_ {in} $ = puissance d'entrée et $ P_ {out} $ = puissance de sortie
Méthode du rapport de puissance
Dans cette méthode, la mesure de l'atténuation se fait en deux étapes.
Step 1 - La puissance d'entrée et de sortie de l'ensemble du banc hyperfréquence se fait sans le dispositif dont l'atténuation doit être calculée.
Step 2 - La puissance d'entrée et de sortie de l'ensemble du banc hyperfréquence se fait avec l'appareil dont l'atténuation doit être calculée.
Le rapport de ces puissances, comparé, donne la valeur de l'atténuation.
Les figures suivantes sont les deux configurations qui expliquent cela.

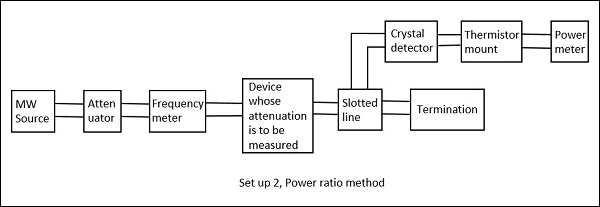
Drawback - Les mesures de puissance et d'atténuation peuvent ne pas être précises, lorsque la puissance d'entrée est faible et l'atténuation du réseau est importante.
Méthode de substitution RF
Dans cette méthode, la mesure de l'atténuation s'effectue en trois étapes.
Step 1 - La puissance de sortie de l'ensemble du banc hyperfréquence est mesurée avec le réseau dont l'atténuation doit être calculée.
Step 2 - La puissance de sortie de l'ensemble du banc hyperfréquence est mesurée en remplaçant le réseau par un atténuateur calibré de précision.
Step 3 - Maintenant, cet atténuateur est réglé pour obtenir la même puissance que celle mesurée avec le réseau.
Les figures suivantes sont les deux configurations qui expliquent cela.
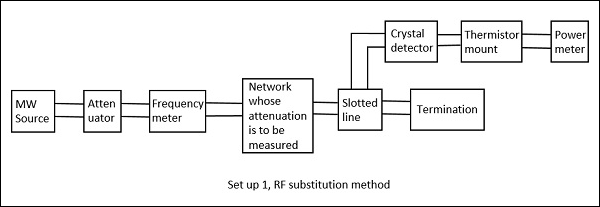
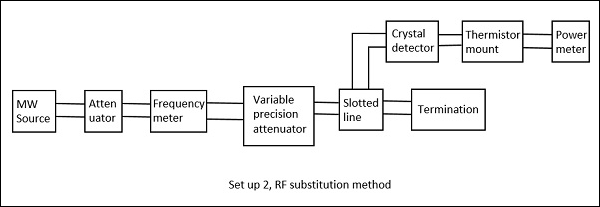
La valeur ajustée sur l'atténuateur donne directement l'atténuation du réseau. L'inconvénient de la méthode ci-dessus est évité ici et c'est donc une meilleure procédure pour mesurer l'atténuation.
Mesure du déphasage
Dans des conditions de travail pratiques, il peut se produire un changement de phase du signal à partir du signal réel. Pour mesurer un tel déphasage, nous utilisons une technique de comparaison, par laquelle nous pouvons calibrer le déphasage.
La configuration pour calculer le déphasage est illustrée dans la figure suivante.
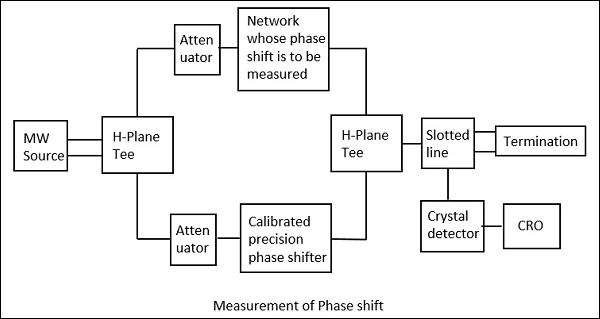
Ici, après que la source hyperfréquence a généré le signal, elle est passée à travers une jonction en T de plan H à partir de laquelle un port est connecté au réseau dont le déphasage doit être mesuré et l'autre port est connecté à un déphaseur de précision réglable.
La sortie démodulée est une onde sinusoïdale de 1 KHz, qui est observée dans le CRO connecté. Ce déphaseur est ajusté de sorte que sa sortie d'onde sinusoïdale de 1 KHz corresponde également à ce qui précède. Une fois l'appariement effectué par observation en CRO bimode, ce déphaseur de précision nous donne la lecture du déphasage. Ceci est clairement compris par la figure suivante.
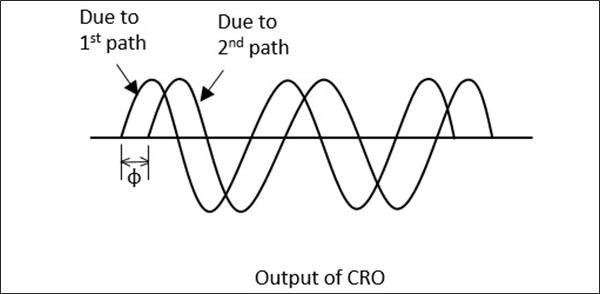
Cette procédure est la plus utilisée dans la mesure du déphasage. Voyons maintenant comment calculer le VSWR.
Mesure de VSWR
Dans toutes les applications pratiques des micro-ondes, tout type de non-correspondance d'impédance conduit à la formation d'ondes stationnaires. La force de ces ondes stationnaires est mesurée par le rapport d'onde stationnaire de tension ($ VSWR $). Le rapport entre la tension maximale et la tension minimale donne le $ VSWR $, qui est noté $ S $.
$$ S = \ frac {V_ {max}} {V_ {min}} = \ frac {1+ \ rho} {1- \ rho} $$
Où, $ \ rho = reflet \: co - efficient = \ frac {P_ {reflété}} {P_ {incident}} $
La mesure de $ VSWR $ peut être effectuée de deux manières, les mesures Low $ VSWR $ et High $ VSWR $.
Mesure d'un VSWR faible (S <10)
La mesure d'un faible $ VSWR $ peut être effectuée en ajustant l'atténuateur pour obtenir une lecture sur un millivoltmètre CC qui est un compteur VSWR. Les lectures peuvent être prises en ajustant la ligne à fente et l'atténuateur de telle sorte que le millivoltmètre CC affiche une lecture pleine échelle ainsi qu'une lecture minimale.
Maintenant, ces deux lectures sont calculées pour connaître le $ VSWR $ du réseau.
Mesure d'un VSWR élevé (S> 10)
La mesure d'un $ VSWR $ élevé dont la valeur est supérieure à 10 peut être mesurée par une méthode appelée double minimum method. Dans cette méthode, la lecture à la valeur minimale est prise, et les lectures au demi-point de la valeur minimale dans la crête avant et la crête après sont également prises. Cela peut être compris par la figure suivante.
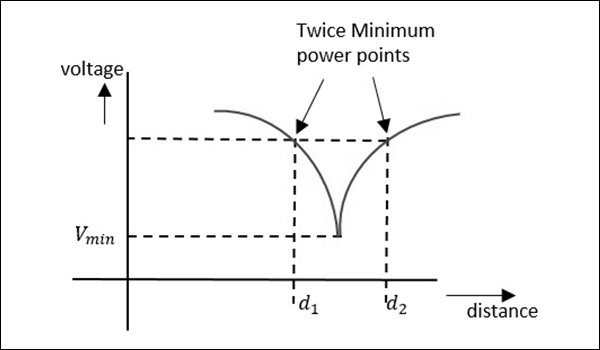
Maintenant, le $ VSWR $ peut être calculé par une relation, donnée comme -
$$ VSWR = \ frac {\ lambda_ {g}} {\ pi (d_2-d_1)} $$
Où, $ \ lambda_g \: est \: la \: guidée \: longueur d'onde $
$$ \ lambda_g = \ frac {\ lambda_0} {\ sqrt {1 - (\ frac {\ lambda_0} {\ lambda_c}) ^ 2}} \ quad où \: \ lambda_0 \: = {c} / {f} $$
Comme les deux points minimaux sont considérés ici, cela s'appelle la méthode du double minimum. Maintenant, apprenons la mesure de l'impédance.
Mesure d'impédance
En dehors de Magic Tee, nous avons deux méthodes différentes, l'une utilise la ligne à fente et l'autre utilise le réflectomètre.
Impédance en utilisant la ligne à fente
Dans cette méthode, l'impédance est mesurée en utilisant une ligne à fente et la charge $ Z_L $ et en utilisant cela, $ V_ {max} $ et $ V_ {min} $ peuvent être déterminés. Dans cette méthode, la mesure de l'impédance se fait en deux étapes.
Step 1 - Détermination de Vmin à l'aide de load $ Z_L $.
Step 2 - Détermination de Vmin en court-circuitant la charge.
Ceci est illustré dans les figures suivantes.
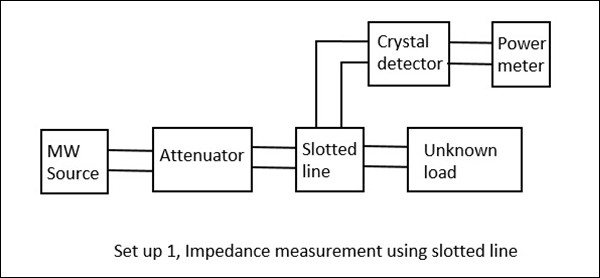
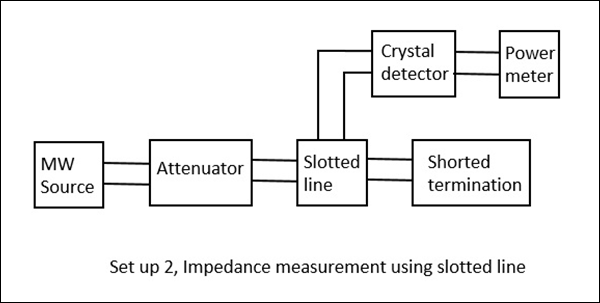
Lorsque nous essayons d'obtenir les valeurs de $ V_ {max} $ et $ V_ {min} $ en utilisant une charge, nous obtenons certaines valeurs. Cependant, si la même chose est faite en court-circuitant la charge, le minimum est décalé, soit vers la droite, soit vers la gauche. Si ce décalage est vers la gauche, cela signifie que la charge est inductive et si c'est le décalage vers la droite, cela signifie que la charge est de nature capacitive. La figure suivante explique cela.
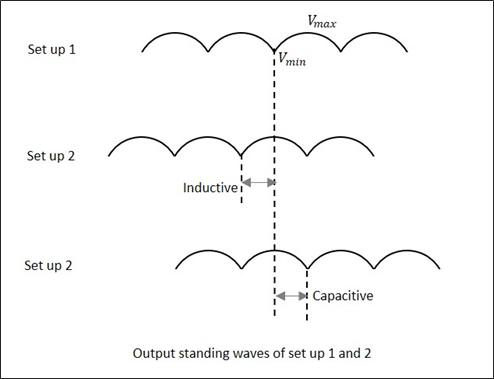
En enregistrant les données, une impédance inconnue est calculée. L'impédance et le coefficient de réflexion $ \ rho $ peuvent être obtenus à la fois en magnitude et en phase.
Impédance à l'aide du réflectomètre
Contrairement à la ligne à fentes, le réflectomètre aide à trouver uniquement l'amplitude de l'impédance et non l'angle de phase. Dans ce procédé, deux coupleurs directionnels identiques mais de direction différente sont pris.
Ces deux coupleurs sont utilisés pour échantillonner la puissance incidente $ P_i $ et la puissance réfléchie $ P_r $ de la charge. Le réflectomètre est connecté comme indiqué dans la figure suivante. Il est utilisé pour obtenir l'amplitude du coefficient de réflexion $ \ rho $, à partir duquel l'impédance peut être obtenue.

À partir de la lecture du réflectomètre, nous avons
$$ \ rho = \ sqrt {\ frac {P_r} {P_i}} $$
A partir de la valeur de $ \ rho $, le $ VSWR $, soit $ S $ et l'impédance peuvent être calculés par
$$ S = \ frac {1+ \ rho} {1- \ rho} \ quad et \ quad \ frac {z-z_g} {z + z_g} = \ rho $$
Où, $ z_g $ est l'impédance d'onde connue et $ z $ est l'impédance inconnue.
Bien que les paramètres d'onde directe et inverse soient observés ici, il n'y aura pas d'interférence due à la propriété directionnelle des coupleurs. L'atténuateur aide à maintenir une faible puissance d'entrée.
Mesure du Q du résonateur de cavité
Bien qu'il existe trois méthodes telles que la méthode de transmission, la méthode d'impédance et la méthode de décroissance ou de décrémentation transitoire pour mesurer Q d'un résonateur à cavité, la méthode la plus simple et la plus suivie est la Transmission Method. Jetons donc un œil à sa configuration de mesure.
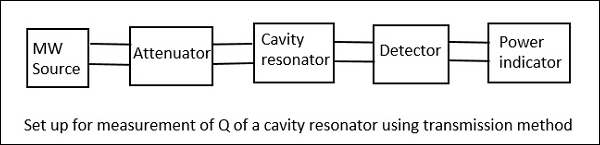
Dans cette méthode, le résonateur à cavité agit comme le dispositif qui transmet. Le signal de sortie est tracé en fonction de la fréquence, ce qui donne une courbe de résonance comme le montre la figure suivante.
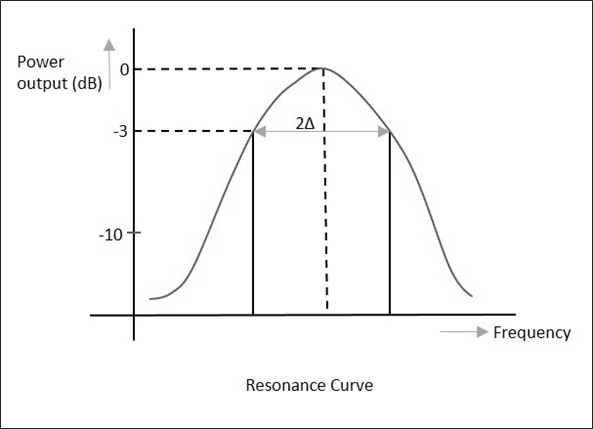
À partir de la configuration ci-dessus, la fréquence du signal de la source de micro-ondes est modifiée, en maintenant le niveau de signal constant, puis la puissance de sortie est mesurée. Le résonateur à cavité est accordé à cette fréquence, et le niveau du signal et la puissance de sortie sont à nouveau notés pour remarquer la différence.
Lorsque la sortie est tracée, la courbe de résonance est obtenue, à partir de laquelle nous pouvons remarquer les valeurs de Half Power Bandwidth (HPBW) $ (2 \ Delta) $.
$$ 2 \ Delta = \ pm \ frac {1} {Q_L} $$
Où, $ Q_L $ est la valeur chargée
$$ ou \ quad Q_L = \ pm \ frac {1} {2 \ Delta} = \ pm \ frac {w} {2 (w-w_0)} $$
Si le couplage entre la source hyperfréquence et la cavité, ainsi que le couplage entre le détecteur et la cavité sont négligés, alors
$$ Q_L = Q_0 \: (déchargé \: Q) $$
Inconvénient
Le principal inconvénient de ce système est que la précision est un peu médiocre dans les systèmes à Q très élevé en raison d'une bande de fonctionnement étroite.
Nous avons couvert de nombreux types de techniques de mesure de différents paramètres. Maintenant, essayons de résoudre quelques exemples de problèmes sur ces derniers.
Dans ce chapitre, amusons-nous en résolvant quelques problèmes numériques liés aux micro-ondes.
Problème 1
Un système de transmission utilisant un guide d'ondes en mode $ TE_ {10} $ de dimensions $ a = 5cm, b = 3cm $ fonctionne à 10GHz. La distance mesurée entre deux points de puissance minimum est1mm on a slotted line. Calculate the VSWR of the system.
Solution
Étant donné que $ f = 10 GHz; a = 5 cm; b = 3 cm $
Pour le guide d'ondes en mode $ TE_ {10} $,
$$ \ lambda_c = 2a = 2 \ fois 5 = 10 cm $$
$$ \ lambda_0 = \ frac {c} {f} = \ frac {3 \ times10 ^ {10}} {10 \ times10 ^ 9} = 3cm $$
$$ d_2-d_1 = 1 mm = 10 ^ {- 1} cm $$
Nous savons
$$ \ lambda_g = \ frac {\ lambda_0} {1 - ({\ lambda_0} / {\ lambda_c}) ^ 2} = \ frac {3} {\ sqrt {1 - ({3} / {10}) ^ 2}} = 3,144 cm $$
Pour la méthode du double minimum, VSWR est donné par
$$ VSWR = \ frac {\ lambda_g} {\ pi (d_2-d_1)} = \ frac {3.144} {\ pi (1 \ times10 ^ {- 1})} = 10.003 = 10 $$
Par conséquent, la valeur VSWR pour le système de transmission donné est de 10.
Problème 2
Dans une configuration pour mesurer l'impédance d'un réflectomètre, quel est le coefficient de réflexion lorsque les sorties de deux coupleurs sont 2mw et 0.5mw respectivement?
Solution
Étant donné que
$$ \ frac {P_i} {100} = 2 mw \ quad et \ quad \ frac {P_r} {100} = 0,5 mw $$
$$ P_i = 2 \ fois 100 mw = 200 mw $$
$$ P_r = 0,5 \ fois 100 mw = 50 mw $$
$$ \ rho = \ sqrt {\ frac {P_r} {P_i}} = \ sqrt {\ frac {50mw} {200mw}} = \ sqrt {0,25} = 0,5 $$
Par conséquent, le coefficient de réflexion $ \ rho $ de la configuration donnée est de 0,5.
Problème 3
Lorsque deux coupleurs identiques sont utilisés dans un guide d'ondes pour échantillonner la puissance incidente comme 3 mw et la puissance réfléchie comme 0.25mw, puis trouvez la valeur de $ VSWR $.
Solution
Nous savons que
$$ \ rho = \ sqrt {\ frac {P_r} {P_i}} = \ sqrt {\ frac {0,25} {3}} = \ sqrt {0,0833} = 0,288 $$
$$ VSWR = S = \ frac {1+ \ rho} {1- \ rho} = \ frac {1 + 0,288} {1-0,288} = \ frac {1,288} {0,712} = 1,80 $$
Par conséquent, la valeur $ VSWR $ pour le système ci-dessus est de 1,80
Problème 4
Deux identiques 30dBLes coupleurs directionnels sont utilisés pour échantillonner la puissance incidente et réfléchie dans un guide d'ondes. La valeur de VSWR est6 et la sortie de la puissance incidente d'échantillonnage du coupleur est 5mw. Quelle est la valeur de la puissance réfléchie?
Solution
Nous savons que
$$ VSWR = S = \ frac {1+ \ rho} {1- \ rho} = 6 $$
$$ (1+ \ rho) = 6 (1- \ rho) = 6 - 6 \ rho $$
$$ 7 \ rho = 5 $$
$$ \ rho = \ frac {5} {7} = 0,174 $$
Pour obtenir la valeur de la puissance réfléchie, nous avons
$$ \ rho = \ sqrt {\ frac {{P_r} / {10 ^ 3}} {{P_i} / {10 ^ 3}}} = \ sqrt {\ frac {P_r} {P_i}} $$
$$ ou \ quad \ rho ^ 2 = \ frac {P_r} {P_i} $$
$$ P_r = \ rho ^ 2.P_i = (0,714) ^ 2,5 = 0,510 \ fois 5 = 2,55 $$
Par conséquent, la puissance réfléchie dans ce guide d'ondes est de 2,55 mW.