Hauteur et distance - Exemples résolus
Q 1 - A partir d'un point situé à 375 mètres du pied d'une tour, le sommet de la tour est observé à un angle d'élévation de 45 °, puis la hauteur (en mètres) de la tour est?
A - 375
B - 450
C - 225
D - 250
Answer - A
Explanation

From the right angled triangle
Tan(45°)= X/375
=> X = 375 mQ 2 - L'angle d'élévation d'une tour en un point situé à 90 m de celle-ci est cot -1 (4/5). Ensuite, la hauteur de la tour est
A - 45
B - 90
C - 112,5
D - 150
Answer - C
Explanation

Let cot-1(4/5) = x
=> cotx = 4/5
=> tan(x) = 5/4
From the right angled triangle
Tan(x) = h/90
=> h = 5/4*90 =112.5 mQ 3 - Sur un terrain plat, l'angle d'élévation du sommet d'une tour est de 30 ° .En se déplaçant de 20 mètres plus près, l'angle d'élévation est de 45 ° .Ensuite, la hauteur de la tour est
A - 10
B - √3
C - 10√3
D - 20√3
Answer - C
Explanation

Let h be the height of tower
From figure.
20 =h ( cot30 - cot60)
20 =h (√3-1/√3)
=> 20√3 = h (3-1)
=> h=10√3.Q 4 - Les angles d'élévation des sommets de deux tours verticales vus du point médian des lignes joignant le pied des tours sont de 45 ° et 60 °. Le rapport de la hauteur des tours est
A - √3: 2
B - √3: 1
C - 2: √3
D - 2: 1
Answer - B
Explanation
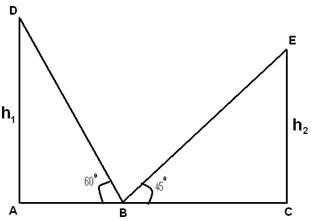
Tan(60)=h1/AB
=> h1=√3AB
Tan(45)=h1/BC
=> h2=BC
h1/ h2=√3/1
=> h1:h2=√3:1Q 5 - Les hauteurs de deux tours sont de 90 mètres et 45 mètres. La ligne joignant leurs sommets fait un angle de 450 avec l'horizontale puis la distance entre les deux tours est
A - 22,5 m
B - 45 m
C - 60 m
D - 30 m
Answer - B
Explanation

Let the distance between the towers be X
From the right angled triangle CFD
Tan(45)= (90-45)/X
=> x=45 metersQ 6 - A partir d'un point P sur un terrain plat, l'angle d'élévation de la tour supérieure est de 60 °. Si la tour mesure 180 m de haut, la distance entre le point P et le pied de la tour est
A - 60√3
B - 40√3
C - 30√3
D - 20√3
Answer - A
Explanation

From ∠APB = 60° and AB = 180 m.
AB/AP= tan 60° =√3
AP=AB/√3 =180/√3=60√3Q 7 - Le sommet d'une tour de 25 mètres de haut fait un angle d'élévation de 450 avec le bas d'un poteau électrique et un angle d'élévation de 30 degrés avec le sommet du poteau. Trouvez la hauteur du poteau électrique.
A - 25√3
B - 25 ((√3-1) / √3)
C - 25 / √3
D - 25 ((1-√3) / √3)
Answer - B
Explanation

Let AB be the tower and CD be the electric pole.
From the figure CA = DE
=> 25/(Tan(45))=(25-h)/(Tan(30))
=> 25 Tan(30) = 25-h
=> h=25-25Tan(30)
=25(1- Tan(30))
=25((√3-1)/√3)Q 8 - Un observateur de 1,4 m de haut est à 10√3 d'une tour. L'angle d'élévation de son oeil au sommet de la tour est de 60 °. Les hauteurs de la tour sont
A - 12,4 m
B - 6,2 m
C - 11,4 √3 m
D - 11,4 m
Answer - D
Explanation

Let AB be the observer and CD be the tower.
Then, CE = AB = 1.4 m,
BE = AC = 10v3 m.
DE/BE=Tan (30) =1/√3
DE=10√3/√3=10
CD=CE+DE=1.4+10=11.4 mQ 9 - Un homme regarde du haut de la tour un bateau s'éloignant de la tour. Le bateau fait l'angle de dépression de 60 ° avec l'œil de l'homme lorsqu'il est à une distance de 75 mètres de la tour. Après 10 secondes, l'angle de dépression devient 45 °. Quelle est la vitesse approximative du bateau, en supposant qu'il roule en eau calme?
A - 54 km / h
B - 64 km / h
C - 24 km / h
D - 19,8 km / h
Answer - D
Explanation

Let AB be the tower and C and D be the positions of the boat.
Distance travelled by boat = CD
From the figure 75tan(60)=(75+CD)tan(45)
=>75√3 = 75+CD
=>CD =55 m
Speed = distance/time=55/10
=5.5 m/sec=19.8 kmphQ 10 - La distance horizontale entre deux tours est de 90 m. La dépression angulaire du sommet du premier vu du haut du second qui mesure 180 m de haut est de 450, puis la hauteur du premier est
A - 90√3 m
B - 45 m
C - 90 m
D - 150 m
Answer - C
Explanation

=>(180-h)/90 = Tan(45)
=> h =90 m- Ajouter des notes
- Marquer cette page
- Signaler une erreur
- Suggestions
Enregistrer Fermer