Techniques d'échantillonnage des signaux
Il existe trois types de techniques d'échantillonnage:
Échantillonnage impulsionnel.
Échantillonnage naturel.
Échantillonnage Flat Top.
Échantillonnage impulsionnel
L'échantillonnage impulsionnel peut être effectué en multipliant le signal d'entrée x (t) par le train d'impulsions $ \ Sigma_ {n = - \ infty} ^ {\ infty} \ delta (t-nT) $ de la période 'T'. Ici, l'amplitude de l'impulsion change par rapport à l'amplitude du signal d'entrée x (t). La sortie de l'échantillonneur est donnée par
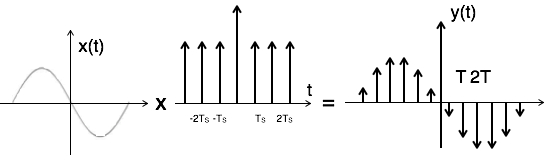
$ y (t) = x (t) × $ train d'impulsions
$ = x (t) × \ Sigma_ {n = - \ infty} ^ {\ infty} \ delta (t-nT) $
$ y (t) = y _ {\ delta} (t) = \ Sigma_ {n = - \ infty} ^ {\ infty} x (nt) \ delta (t-nT) \, ... \, ... 1 $
Pour obtenir le spectre du signal échantillonné, considérons la transformée de Fourier de l'équation 1 des deux côtés
$ Y (\ omega) = {1 \ sur T} \ Sigma_ {n = - \ infty} ^ {\ infty} X (\ omega - n \ omega_s) $
C'est ce qu'on appelle l'échantillonnage idéal ou l'échantillonnage impulsionnel. Vous ne pouvez pas l'utiliser en pratique car la largeur d'impulsion ne peut pas être nulle et la génération d'un train d'impulsions n'est pratiquement pas possible.
Échantillonnage naturel
L'échantillonnage naturel est similaire à l'échantillonnage impulsionnel, sauf que le train d'impulsions est remplacé par un train d'impulsions de période T. c.-à-d. Que vous multipliez le signal d'entrée x (t) en train d'impulsions $ \ Sigma_ {n = - \ infty} ^ {\ infty} P ( t-nT) $ comme indiqué ci-dessous

La sortie de l'échantillonneur est
$ y (t) = x (t) \ times \ text {train d'impulsions} $
$ = x (t) \ fois p (t) $
$ = x (t) \ times \ Sigma_ {n = - \ infty} ^ {\ infty} P (t-nT) \, ... \, ... (1) $
La représentation exponentielle de la série de Fourier de p (t) peut être donnée comme
$ p (t) = \ Sigma_ {n = - \ infty} ^ {\ infty} F_n e ^ {jn \ omega_s t} \, ... \, ... (2) $
$ = \ Sigma_ {n = - \ infty} ^ {\ infty} F_n e ^ {j 2 \ pi nf_s t} $
Où $ F_n = {1 \ over T} \ int _ {- T \ over 2} ^ {T \ over 2} p (t) e ^ {- jn \ omega_s t} dt $
$ = {1 \ sur TP} (n \ omega_s) $
Remplacer la valeur F n dans l'équation 2
$ \ donc p (t) = \ Sigma_ {n = - \ infty} ^ {\ infty} {1 \ over T} P (n \ omega_s) e ^ {jn \ omega_s t} $
$ = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) e ^ {jn \ omega_s t} $
Remplacez p (t) dans l'équation 1
$ y (t) = x (t) \ fois p (t) $
$ = x (t) \ times {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, e ^ {jn \ omega_s t} $
$ y (t) = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, x (t) \, e ^ {jn \ omega_s t} $
Pour obtenir le spectre du signal échantillonné, considérez la transformée de Fourier des deux côtés.
$ FT \, [y (t)] = FT [{1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, x (t) \, e ^ { jn \ omega_s t}] $
$ = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, FT \, [x (t) \, e ^ {jn \ omega_s t}] $
Selon la propriété de décalage de fréquence
$ FT \, [x (t) \, e ^ {jn \ omega_s t}] = X [\ omega-n \ omega_s] $
$ \ donc \, Y [\ omega] = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, X [\ omega-n \ omega_s] $
Échantillonnage à plat
Pendant la transmission, un bruit est introduit au sommet de l'impulsion de transmission qui peut être facilement supprimé si l'impulsion est sous la forme d'un sommet plat. Ici, le haut des échantillons est plat c'est-à-dire qu'ils ont une amplitude constante. Par conséquent, il est appelé échantillonnage à sommet plat ou échantillonnage pratique. L'échantillonnage à sommet plat utilise un circuit d'échantillonnage et de maintien.

Théoriquement, le signal échantillonné peut être obtenu par convolution de l'impulsion rectangulaire p (t) avec un signal idéalement échantillonné, disons y δ (t) comme indiqué sur le diagramme:
ie $ y (t) = p (t) \ times y_ \ delta (t) \, ... \, ... (1) $

Pour obtenir le spectre échantillonné, considérez la transformée de Fourier des deux côtés pour l'équation 1
$ Y [\ omega] = FT \, [P (t) \ fois y_ \ delta (t)] $
Par la connaissance de la propriété de convolution,
$ Y [\ omega] = P (\ omega) \, Y_ \ delta (\ omega) $
Ici $ P (\ omega) = T Sa ({\ omega T \ over 2}) = 2 \ sin \ omega T / \ omega $
Taux Nyquist
C'est la fréquence d'échantillonnage minimale à laquelle le signal peut être converti en échantillons et peut être récupéré sans distorsion.
Taux de Nyquist f N = 2f m hz
Intervalle de Nyquist = $ {1 \ over fN} $ = $ {1 \ over 2fm} $ secondes.
Échantillons de signaux Band Pass
Dans le cas de signaux passe-bande, le spectre du signal passe-bande X [ω] = 0 pour les fréquences en dehors de la plage f 1 ≤ f ≤ f 2 . La fréquence f 1 est toujours supérieure à zéro. De plus, il n'y a pas d'effet d'alias lorsque f s > 2f 2 . Mais cela présente deux inconvénients:
Le taux d'échantillonnage est grand proportionnellement à f 2 . Cela a des limites pratiques.
Le spectre du signal échantillonné présente des lacunes spectrales.
Pour surmonter cela, le théorème de la bande passante indique que le signal d'entrée x (t) peut être converti en ses échantillons et peut être récupéré sans distorsion lorsque la fréquence d'échantillonnage f s <2f 2 .
Également,
$$ f_s = {1 \ sur T} = {2f_2 \ sur m} $$
Où m est le plus grand entier <$ {f_2 \ sur B} $
et B est la bande passante du signal. Si f 2 = KB, alors
$$ f_s = {1 \ sur T} = {2 Ko \ sur m} $$
Pour les signaux passe-bande de largeur de bande 2f m et la fréquence d'échantillonnage minimale f s = 2 B = 4f m ,
le spectre du signal échantillonné est donné par $ Y [\ omega] = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} \, X [\ omega - 2nB] $