Propriétés des transformations en Z

Z-Transform a les propriétés suivantes:

Propriété de linéarité

Si $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

et $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $

Alors la propriété de linéarité indique que

$ a \, x (n) + b \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} a \, X (Z) + b \, Y (Z) $

Propriété de décalage temporel

Si $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Ensuite, la propriété Time shifting indique que

$ x (nm) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} z ^ {- m} X (Z) $

Multiplication par propriété de séquence exponentielle

Si $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Ensuite, la multiplication par une propriété de séquence exponentielle indique que

$ a ^ n \,. x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z / a) $

Propriété d'inversion de temps

Si $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Ensuite, la propriété d'inversion de temps indique que

$ x (-n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (1 / Z) $

Différenciation dans le domaine Z OU multiplication par n propriété

Si $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

Ensuite, la multiplication par n ou la différenciation dans la propriété du domaine z indique que

$ n ^ kx (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} [-1] ^ kz ^ k {d ^ k X (Z) \ over dZ ^ K} $

Propriété de convolution

Si $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

et $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $

Ensuite, la propriété de convolution indique que

$ x (n) * y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z) $

Propriété de corrélation

Si $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

et $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $

Ensuite, la propriété de corrélation indique que

$ x (n) \ otimes y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z ^ {- 1}) $

Théorèmes de la valeur initiale et de la valeur finale

Les théorèmes de valeur initiale et de valeur finale de la transformée en z sont définis pour le signal causal.

Théorème de la valeur initiale

Pour un signal causal x (n), le théorème de la valeur initiale indique que

$ x (0) = \ lim_ {z \ to \ infty} ⁡X (z) $

Ceci est utilisé pour trouver la valeur initiale du signal sans prendre de transformation en z inverse

Théorème de la valeur finale

Pour un signal causal x (n), le théorème de la valeur finale déclare que

$ x (\ infty) = \ lim_ {z \ à 1} [z-1] ⁡X (z) $

Ceci est utilisé pour trouver la valeur finale du signal sans prendre de transformation en z inverse.

Région de convergence (ROC) de Z-Transform

La plage de variation de z pour laquelle converge la transformée z est appelée région de convergence de la transformée z.

Propriétés du ROC des transformations en Z

Le ROC de la transformée z est indiqué par un cercle dans le plan z.
ROC ne contient aucun pôle.
Si x (n) est une séquence causale de durée finie ou une séquence du côté droit, alors le ROC est le plan z entier sauf à z = 0.
Si x (n) est une séquence anti-causale de durée finie ou une séquence du côté gauche, alors le ROC est le plan z entier sauf à z = ∞.
Si x (n) est une suite causale de durée infinie, ROC est extérieur au cercle de rayon aie | z | > a.
Si x (n) est une suite anti-causale de durée infinie, ROC est à l'intérieur du cercle de rayon aie | z | <a.
Si x (n) est une séquence à deux côtés de durée finie, alors le ROC est le plan z entier sauf à z = 0 & z = ∞.

Le concept de ROC peut être expliqué par l'exemple suivant:

Example 1: Trouver z-transform et ROC de $ a ^ nu [n] + a ^ {-} nu [-n-1] $

$ ZT [a ^ nu [n]] + ZT [a ^ {- n} u [-n-1]] = {Z \ sur Za} + {Z \ sur Z {-1 \ sur a}} $

$$ ROC: | z | \ gt a \ quad \ quad ROC: | z | \ lt {1 \ sur un} $$

Le tracé de ROC a deux conditions comme a> 1 et a <1, car vous ne connaissez pas a.

Dans ce cas, il n'y a pas de combinaison ROC.

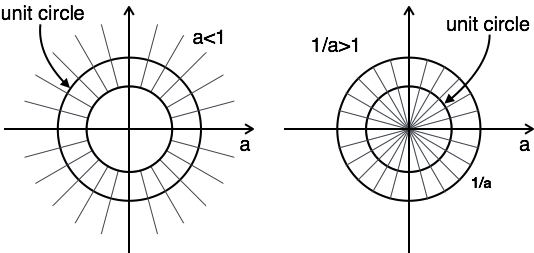
Ici, la combinaison de ROC est de $ a \ lt | z | \ lt {1 \ sur un} $

Par conséquent, pour ce problème, la transformée en z est possible lorsque a <1.

Causalité et stabilité

La condition de causalité pour les systèmes LTI à temps discret est la suivante:

Un système LTI à temps discret est causal lorsque

ROC est en dehors du pôle le plus extérieur.
Dans La fonction de transfert H [Z], l'ordre du numérateur ne peut pas être supérieur à l'ordre du dénominateur.

Condition de stabilité pour les systèmes LTI à temps discret

Un système LTI à temps discret est stable lorsque

sa fonction système H [Z] inclut le cercle unitaire | z | = 1.
tous les pôles de la fonction de transfert se trouvaient à l'intérieur du cercle unitaire | z | = 1.

Transformation en Z des signaux de base

x (t)	X [Z]
$ \ delta $	1
$ u (n) $	$ {Z \ sur Z-1} $
$ u (-n-1) $	$ - {Z \ sur Z-1} $
$ \ delta (nm) $	$ z ^ {- m} $
$ a ^ nu [n] $	$ {Z \ over Za} $
$ a ^ nu [-n-1] $	$ - {Z \ sur Za} $
$ n \, a ^ nu [n] $	$ {aZ \ over \| Za \| ^ 2} $
$ n \, a ^ nu [-n-1] $	$ - {aZ \ over \| Za \| ^ 2} $
$ a ^ n \ cos \ omega nu [n] $	$ {Z ^ 2-aZ \ cos \ omega \ over Z ^ 2-2aZ \ cos \ omega + a ^ 2} $
$ a ^ n \ sin \ omega nu [n] $	$ {aZ \ sin \ omega \ over Z ^ 2 -2aZ \ cos \ omega + a ^ 2} $