एक मिश्रित संख्या और एक छायांकित क्षेत्र के लिए एक अनुचित अंश लिखना
इस पाठ में, हम सर्कल, आयताकार स्ट्रिप्स आदि के आंकड़ों पर विचार करते हैं, जिनमें से कुछ को पूरे छायांकित किया जाता है और कुछ को आंशिक रूप से छायांकित किया जाता है। पूरे और आंशिक रूप से छायांकित क्षेत्रों के संयोजन के लिए, हम संबंधित मिश्रित संख्या और अनुचित अंश लिखते हैं जो उनका प्रतिनिधित्व करेंगे।
के लिये example, अगर दो पूरे छायांकित आंकड़े और एक तीन-पांचवें फ्रैक्शनल शेडेड आंकड़ा दिया जाता है, तो हम मिश्रित संख्या $ 2 \ frac {4} {5} $ और अनुचित अंश $ \ frac {14} {5} $ के साथ इस तरह के संयोजन का प्रतिनिधित्व करते हैं ।
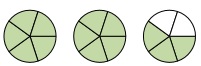
नीचे दिए गए छायांकित क्षेत्र के लिए एक मिश्रित संख्या लिखें
उपाय
Step 1:
दो छायांकित पूरे वृत्त और तीन-पांचवें छायांकित वृत्त हैं।
Step 2:
$ 1 + 1 + \ frac {3} {5} = 2 \ frac {3} {5} $
तो, आंकड़ों के इस संयोजन को मिश्रित संख्या $ 2 \ frac {3} {5} $ द्वारा दर्शाया गया है ।
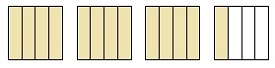
नीचे दिए गए छायांकित क्षेत्र के लिए एक अनुचित अंश लिखें
उपाय
Step 1:
तीन छायांकित पूरे आयताकार स्ट्रिप्स और एक-चौथाई छायांकित पट्टी हैं।
Step 2:
$ 1 + 1 + 1 + \ frac {1} {4} = 3 \ frac {1} {4} $
तो, आंकड़ों के इस संयोजन को मिश्रित संख्या $ 3 \ frac {1} {4} $ द्वारा दर्शाया गया है
Step 3:
$ 3 \ frac {1} {4} $ एक एल्गोरिथ्म का उपयोग करते हुए अनुचित अंश के रूप में निम्नानुसार लिखा जाता है।
$ 3 \ frac {1} {4} = \ frac {\ बाईं (3 \ 4 बार + 1 \ दाएँ)} {4} = \ frac {13} {4} $
तो, दिए गए छायांकित क्षेत्र का प्रतिनिधित्व करने वाला अनुचित अंश $ \ frac {13} {4} $ है ।