Panduan Cepat

Dalam dunia elektronik modern, istilahnya Digital umumnya dikaitkan dengan komputer karena istilah Digitalditurunkan dari cara komputer melakukan operasi, dengan menghitung angka. Selama bertahun-tahun, penerapan elektronik digital hanya ada di sistem komputer. Tapi sekarang-a-hari, elektronik digital digunakan di banyak aplikasi lain. Berikut adalah beberapa contoh di manaDigital electronics banyak digunakan.

• Pengendalian proses industri
• Sistem militer
• Television
• Sistem komunikasi
• Peralatan medis
• Radar
• Navigation

Sinyal

Signaldapat didefinisikan sebagai besaran fisik, yang berisi beberapa informasi. Ini adalah fungsi dari satu atau lebih dari satu variabel independen. Sinyal terdiri dari dua jenis.

• Sinyal analog
• Sinyal Digital

Sinyal analog

Sebuah analog signaldidefinisikan sebagai sinyal yang memiliki nilai kontinu. Sinyal analog dapat memiliki nilai berbeda dalam jumlah tak terbatas. Dalam skenario dunia nyata, sebagian besar hal yang diamati di alam adalah analog. Contoh sinyal analog berikut ini.

• Temperature
• Pressure
• Distance
• Sound
• Voltage
• Current
• Power

Representasi grafis dari Sinyal Analog (Suhu)

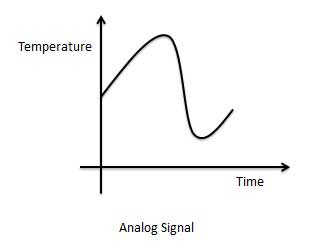
Sirkuit yang memproses sinyal analog disebut sebagai sirkuit atau sistem analog. Contoh sistem analog berikut ini.

• Filter
• Amplifiers
• Penerima televisi
• Pengontrol kecepatan motor

Kerugian Sistem Analog

• Akurasi kurang
• Fleksibilitas kurang
• Lebih banyak efek noise
• Lebih banyak distorsi
• Lebih banyak efek cuaca

Sinyal Digital

SEBUAH digital signaldidefinisikan sebagai sinyal yang hanya memiliki sejumlah nilai berbeda yang terbatas. Sinyal digital bukanlah sinyal kontinu. Dalam kalkulator elektronik digital, input diberikan dengan bantuan sakelar. Input ini diubah menjadi sinyal listrik yang memiliki dua nilai atau level diskrit. Salah satunya dapat disebut level rendah dan yang lainnya disebut level tinggi. Sinyal akan selalu menjadi salah satu dari dua level. Jenis sinyal ini disebut sinyal digital. Contoh sinyal digital berikut ini.

• Sinyal Biner
• Sinyal Oktal
• Sinyal Heksadesimal

Representasi grafis dari Sinyal Digital (Biner)

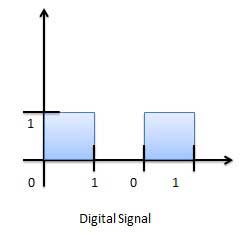
Sirkuit yang memproses sinyal digital disebut sistem digital atau sirkuit digital. Contoh dari sistem digital berikut ini.

• Registers
• Flip-flop
• Counters
• Microprocessors

Keuntungan Sistem Digital

• Lebih akurat
• Lebih banyak fleksibilitas
• Lebih sedikit distorsi
• Mudah berkomunikasi
• Kemungkinan penyimpanan informasi

Perbandingan Sinyal Analog dan Digital

SN	Sinyal analog	Sinyal Digital
1	Sinyal analog memiliki nilai yang tak terbatas.	Sinyal digital memiliki jumlah nilai yang terbatas.
2	Sinyal analog memiliki sifat kontinyu.	Sinyal digital memiliki sifat diskrit.
3	Sinyal analog dihasilkan oleh transduser dan generator sinyal.	Sinyal digital dihasilkan oleh konverter A ke D.
4	Contoh sinyal analog - gelombang sinus, gelombang segitiga.	Contoh sinyal digital - sinyal biner.

Sistem digital dapat memahami sistem bilangan posisional hanya di mana terdapat beberapa simbol yang disebut angka dan simbol-simbol ini mewakili nilai yang berbeda tergantung pada posisi yang mereka tempati dalam bilangan tersebut.

Nilai dari setiap digit angka dapat ditentukan menggunakan

• Angka

• Posisi digit dalam nomor tersebut

• Basis sistem bilangan (di mana basis didefinisikan sebagai jumlah total digit yang tersedia dalam sistem bilangan).

Sistem Angka Desimal

Sistem bilangan yang kita gunakan dalam kehidupan sehari-hari adalah sistem bilangan desimal. Sistem bilangan desimal berbasis 10 karena menggunakan 10 digit dari 0 sampai 9. Dalam sistem bilangan desimal, posisi berurutan di sebelah kiri koma desimal mewakili satuan, puluhan, ratusan, ribuan, dan seterusnya.

Setiap posisi mewakili kekuatan tertentu dari alas (10). Misalnya angka desimal 1234 terdiri dari angka 4 pada posisi satuan, 3 pada posisi puluhan, 2 pada posisi ratusan, dan 1 pada posisi ribuan, dan nilainya dapat dituliskan sebagai

(1&times1000) + (2&times100) + (3&times10) + (4&timesl)
(1&times103) + (2&times102) + (3&times101)  + (4&timesl00)
1000 + 200 + 30 + 1
1234

Sebagai pemrogram komputer atau profesional TI, Anda harus memahami sistem bilangan berikut yang sering digunakan di komputer.

SN	Sistem & Deskripsi Angka
1	Binary Number System Base 2. Digit yang digunakan: 0, 1
2	Octal Number System Base 8. Digit yang digunakan: 0 sampai 7
3	Hexa Decimal Number System Dasar 16. Digit yang digunakan: 0 sampai 9, Huruf yang digunakan: A- F

Sistem Bilangan Biner

Karakteristik

• Menggunakan dua digit, 0 dan 1.

• Juga disebut sistem bilangan basis 2

• Setiap posisi dalam bilangan biner mewakili pangkat 0 dari basis (2). Contoh: 2 ⁰

• Posisi terakhir dalam bilangan biner mewakili pangkat x dari alas (2). Contoh: 2 ^x dimana x mewakili posisi terakhir - 1.

Contoh

Bilangan Biner: 10101 ₂

Menghitung Setara Desimal -

Langkah	Bilangan Biner	Angka desimal
Langkah 1	10101 2	((1 × 2 4 ) + (0 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 )) 10
Langkah 2	10101 2	(16 + 0 + 4 + 0 + 1) 10
LANGKAH 3	10101 2	21 10

Note:10101 ₂ biasanya ditulis sebagai 10101.

Sistem Angka Oktal

Karakteristik

• Menggunakan delapan digit, 0,1,2,3,4,5,6,7.

• Juga disebut sistem bilangan basis 8

• Setiap posisi dalam bilangan oktal mewakili pangkat 0 dari basis (8). Contoh: 8 ⁰

• Posisi terakhir dalam bilangan oktal mewakili pangkat x dari alas (8). Contoh: 8 ^x dimana x mewakili posisi terakhir - 1.

Contoh

Nomor Oktal - 12570 ₈

Menghitung Setara Desimal -

Langkah	Nomor Oktal	Angka desimal
Langkah 1	12570 8	((1 × 8 4 ) + (2 × 8 3 ) + (5 × 8 2 ) + (7 × 8 1 ) + (0 × 8 0 )) 10
Langkah 2	12570 8	(4096 + 1024 + 320 + 56 + 0) 10
LANGKAH 3	12570 8	5496 10

Note:12570 ₈ biasanya ditulis sebagai 12570.

Sistem Angka Heksadesimal

Karakteristik

• Menggunakan 10 digit dan 6 huruf, 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F.

• Huruf mewakili angka mulai dari 10. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.

• Juga disebut sistem bilangan basis 16.

• Setiap posisi dalam bilangan heksadesimal mewakili pangkat 0 dari basis (16). Contoh 16 ⁰ .

• Posisi terakhir dalam bilangan heksadesimal mewakili pangkat x dari basis (16). Contoh 16 ^x dimana x mewakili posisi terakhir - 1.

Contoh -

Bilangan Heksadesimal: 19FDE ₁₆

Menghitung Setara Desimal -

Langkah	Bilangan Heksadesimal	Angka desimal
Langkah 1	19FDE 16	((1 × 16 4 ) + (9 × 16 3 ) + (F × 16 2 ) + (D × 16 1 ) + (E × 16 0 )) 10
Langkah 2	19FDE 16	((1 × 16 4 ) + (9 × 16 3 ) + (15 × 16 2 ) + (13 × 16 1 ) + (14 × 16 0 )) 10
LANGKAH 3	19FDE 16	(65536 + 36864 + 3840 + 208 + 14) 10
LANGKAH 4	19FDE 16	106462 10

Note −19FDE ₁₆ biasanya ditulis sebagai 19FDE.

Ada banyak metode atau teknik yang dapat digunakan untuk mengonversi bilangan dari satu basis ke basis lainnya. Kami akan menunjukkan di sini yang berikut -

• Desimal ke Sistem Basis Lain
• Sistem Basis Lain ke Desimal
• Sistem Basis Lainnya ke Non-Desimal
• Metode pintas - Biner ke Oktal
• Metode pintas - Oktal ke Biner
• Metode pintas - Biner ke Heksadesimal
• Metode pintas - Heksadesimal ke Biner

Desimal ke Sistem Basis Lain

Langkah

• Step 1 - Bagi angka desimal yang akan dikonversi dengan nilai basis baru.

• Step 2 - Dapatkan sisa dari Langkah 1 sebagai digit paling kanan (digit paling signifikan) dari bilangan dasar baru.

• Step 3 - Bagilah hasil bagi dari pembagian sebelumnya dengan basis baru.

• Step 4 - Catat sisa dari Langkah 3 sebagai digit berikutnya (ke kiri) dari bilangan pokok yang baru.

Ulangi Langkah 3 dan 4, dapatkan sisa dari kanan ke kiri, hingga hasil bagi menjadi nol pada Langkah 3.

Sisa terakhir yang diperoleh akan menjadi Digit Paling Signifikan (MSD) dari bilangan dasar baru.

Contoh -

Angka Desimal: 29 ₁₀

Menghitung Setara Biner -

Langkah	Operasi	Hasil	Sisa
Langkah 1	29/2	14	1
Langkah 2	14/2	7	0
LANGKAH 3	7/2	3	1
LANGKAH 4	3/2	1	1
LANGKAH 5	1/2	0	1

Sebagaimana disebutkan pada Langkah 2 dan 4, sisa harus disusun dalam urutan terbalik sehingga sisa pertama menjadi Angka Signifikan Terkecil (LSD) dan sisa terakhir menjadi Angka Paling Signifikan (MSD).

Bilangan Desimal - 29 ₁₀ = Bilangan Biner - 11101 ₂ .

Sistem Basis Lainnya ke Sistem Desimal

Langkah

• Step 1 - Tentukan nilai kolom (posisi) dari setiap digit (ini tergantung pada posisi digit dan basis sistem bilangan).

• Step 2 - Kalikan nilai kolom yang diperoleh (pada Langkah 1) dengan angka di kolom yang sesuai.

• Step 3 - Jumlahkan produk yang dihitung pada Langkah 2. Jumlahnya adalah nilai ekuivalen dalam desimal.

Contoh

Bilangan Biner - 11101 ₂

Menghitung Setara Desimal -

Langkah	Bilangan Biner	Angka desimal
Langkah 1	11101 2	((1 × 2 4 ) + (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 )) 10
Langkah 2	11101 2	(16 + 8 + 4 + 0 + 1) 10
LANGKAH 3	11101 2	29 10

Bilangan Biner - 11101 ₂ = Bilangan Desimal - 29 ₁₀

Sistem Basis Lainnya ke Sistem Non-Desimal

Langkah

• Step 1 - Ubah bilangan asli menjadi bilangan desimal (basis 10).

• Step 2 - Ubah angka desimal yang diperoleh menjadi angka basis baru.

Contoh

Nomor Oktal - 25 ₈

Menghitung Setara Biner -

Langkah 1 - Ubah ke Desimal

Langkah	Nomor Oktal	Angka desimal
Langkah 1	25 8	((2 × 8 1 ) + (5 × 8 0 )) 10
Langkah 2	25 8	(16 + 5) 10
LANGKAH 3	25 8	21 10

Angka Oktal - 25 ₈ = Angka Desimal - 21 ₁₀

Langkah 2 - Ubah Desimal ke Biner

Langkah	Operasi	Hasil	Sisa
Langkah 1	21/2	10	1
Langkah 2	10/2	5	0
LANGKAH 3	5/2	2	1
LANGKAH 4	2/2	1	0
LANGKAH 5	1/2	0	1

Bilangan Desimal - 21 ₁₀ = Bilangan Biner - 10101 ₂

Bilangan Oktal - 25 ₈ = Bilangan Biner - 10101 ₂

Metode pintas - Biner ke Oktal

Langkah

• Step 1 - Bagilah digit biner menjadi tiga kelompok (mulai dari kanan).

• Step 2 - Ubah setiap kelompok dari tiga digit biner menjadi satu digit oktal.

Contoh

Bilangan Biner - 10101 ₂

Menghitung Setara Oktal -

Langkah	Bilangan Biner	Nomor Oktal
Langkah 1	10101 2	010 101
Langkah 2	10101 2	2 8 5 8
LANGKAH 3	10101 2	25 8

Bilangan Biner - 10101 ₂ = Nomor Oktal - 25 ₈

Metode pintas - Oktal ke Biner

Langkah

• Step 1 - Ubah setiap digit oktal menjadi 3 digit angka biner (digit oktal dapat diperlakukan sebagai desimal untuk konversi ini).

• Step 2 - Gabungkan semua kelompok biner yang dihasilkan (masing-masing 3 digit) menjadi satu bilangan biner.

Contoh

Nomor Oktal - 25 ₈

Menghitung Setara Biner -

Langkah	Nomor Oktal	Bilangan Biner
Langkah 1	25 8	2 10 5 10
Langkah 2	25 8	010 2 101 2
LANGKAH 3	25 8	010101 2

Bilangan Oktal - 25 ₈ = Bilangan Biner - 10101 ₂

Metode pintas - Biner ke Heksadesimal

Langkah

• Step 1 - Bagilah digit biner menjadi empat kelompok (mulai dari kanan).

• Step 2 - Ubah setiap grup yang terdiri dari empat digit biner menjadi satu simbol heksadesimal.

Contoh

Bilangan Biner - 10101 ₂

Menghitung Setara heksadesimal -

Langkah	Bilangan Biner	Bilangan Heksadesimal
Langkah 1	10101 2	0001 0101
Langkah 2	10101 2	1 10 5 10
LANGKAH 3	10101 2	15 16

Bilangan Biner - 10101 ₂ = Bilangan Heksadesimal - 15 ₁₆

Metode pintas - Heksadesimal ke Biner

Langkah

• Step 1 - Ubah setiap digit heksadesimal menjadi 4 digit angka biner (digit heksadesimal dapat diperlakukan sebagai desimal untuk konversi ini).

• Step 2 - Gabungkan semua kelompok biner yang dihasilkan (masing-masing 4 digit) menjadi satu nomor biner.

Contoh

Bilangan Heksadesimal - 15 ₁₆

Menghitung Setara Biner -

Langkah	Bilangan Heksadesimal	Bilangan Biner
Langkah 1	15 16	1 10 5 10
Langkah 2	15 16	0001 2 0101 2
LANGKAH 3	15 16	00010101 2

Bilangan Heksadesimal - 15 ₁₆ = Bilangan Biner - 10101 ₂

Dalam pengkodean, ketika angka, huruf atau kata diwakili oleh sekelompok simbol tertentu, dikatakan bahwa angka, huruf atau kata sedang dikodekan. Kelompok simbol disebut sebagai kode. Data digital direpresentasikan, disimpan dan ditransmisikan sebagai kelompok bit biner. Grup ini juga disebut sebagaibinary code. Kode biner diwakili oleh angka serta huruf alfanumerik.

Keuntungan dari Kode Biner

Berikut adalah daftar keuntungan yang ditawarkan oleh kode biner.

• Kode biner cocok untuk aplikasi komputer.

• Kode biner cocok untuk komunikasi digital.

• Kode biner membuat analisis dan perancangan rangkaian digital jika kita menggunakan kode biner.

• Karena hanya 0 & 1 yang digunakan, implementasi menjadi mudah.

Klasifikasi kode biner

Kode-kode tersebut secara luas dikategorikan ke dalam empat kategori berikut.

• Kode Tertimbang
• Kode Tidak Berbobot
• Kode Desimal Berkode Biner
• Kode Alfanumerik
• Kesalahan Mendeteksi Kode
• Kesalahan Mengoreksi Kode

Kode Tertimbang

Kode biner tertimbang adalah kode biner yang mematuhi prinsip bobot posisi. Setiap posisi angka mewakili bobot tertentu. Beberapa sistem kode digunakan untuk menyatakan angka desimal 0 sampai 9. Dalam kode ini setiap angka desimal diwakili oleh sekelompok empat bit.

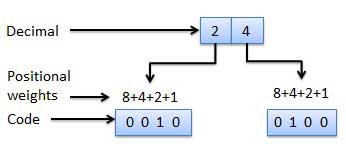
Kode Tidak Berbobot

Dalam jenis kode biner ini, bobot posisi tidak ditetapkan. Contoh kode tidak berbobot adalah kode Kelebihan-3 dan kode Gray.

Kelebihan-3 kode

Kode Kelebihan-3 juga disebut sebagai kode XS-3. Ini adalah kode tanpa bobot yang digunakan untuk menyatakan angka desimal. Kata kode Kelebihan-3 berasal dari 8421 kata kode BCD yang menambahkan (0011) ₂ atau (3) 10 ke setiap kata kode pada 8421. Kode kelebihan-3 diperoleh sebagai berikut -

Contoh

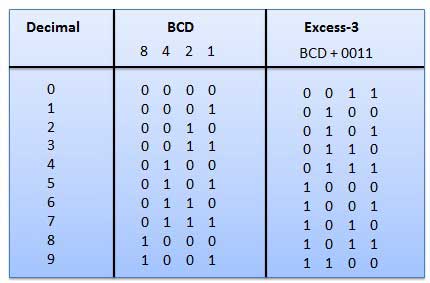
Kode Abu-abu

Ini adalah kode tidak berbobot dan itu bukan kode aritmatika. Itu berarti tidak ada bobot khusus yang ditetapkan ke posisi bit. Ini memiliki fitur yang sangat istimewa, hanya satu bit yang akan berubah setiap kali bilangan desimal bertambah seperti yang ditunjukkan pada gambar. Karena hanya satu bit yang berubah pada satu waktu, kode abu-abu disebut sebagai kode jarak satuan. Kode abu-abu adalah kode siklik. Kode abu-abu tidak dapat digunakan untuk operasi aritmatika.

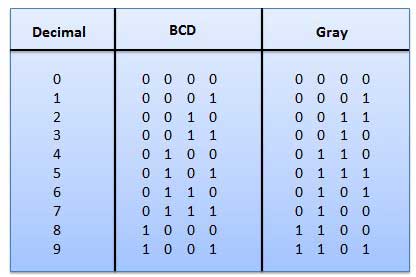
Penerapan kode Gray

• Kode abu-abu populer digunakan dalam encoder posisi poros.

• Encoder posisi poros menghasilkan kata kode yang mewakili posisi sudut poros.

Kode Binary Coded Decimal (BCD)

Dalam kode ini setiap digit desimal diwakili oleh bilangan biner 4-bit. BCD adalah cara untuk mengekspresikan setiap angka desimal dengan kode biner. Dalam BCD, dengan empat bit kita dapat merepresentasikan enam belas angka (0000 sampai 1111). Tetapi dalam kode BCD hanya sepuluh pertama yang digunakan (0000 hingga 1001). Enam kombinasi kode yang tersisa yaitu 1010 hingga 1111 tidak valid di BCD.

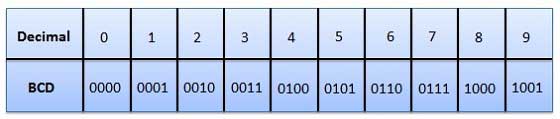
Keuntungan dari Kode BCD

• Ini sangat mirip dengan sistem desimal.
• Kita perlu mengingat angka desimal biner dari 0 sampai 9 saja.

Kerugian dari Kode BCD

• Penjumlahan dan pengurangan BCD memiliki aturan yang berbeda.

• Aritmatika BCD sedikit lebih rumit.

• BCD membutuhkan lebih banyak jumlah bit daripada biner untuk mewakili bilangan desimal. Jadi BCD kurang efisien dibandingkan biner.

Kode alfanumerik

Digit atau bit biner hanya dapat mewakili dua simbol karena hanya memiliki dua status '0' atau '1'. Tetapi ini tidak cukup untuk komunikasi antara dua komputer karena di sana kita membutuhkan lebih banyak simbol untuk komunikasi. Simbol-simbol ini diperlukan untuk mewakili 26 huruf besar dan kecil, angka dari 0 sampai 9, tanda baca dan simbol lainnya.

Kode alfanumerik adalah kode yang merepresentasikan angka dan karakter alfabet. Kebanyakan kode tersebut juga mewakili karakter lain seperti simbol dan berbagai instruksi yang diperlukan untuk menyampaikan informasi. Kode alfanumerik setidaknya harus mewakili 10 digit dan 26 huruf alfabet, artinya total 36 item. Tiga kode alfanumerik berikut ini sangat umum digunakan untuk representasi data.

• Kode Standar Amerika untuk Pertukaran Informasi (ASCII).
• Extended Binary Coded Decimal Interchange Code (EBCDIC).
• Lima bit Kode Baudot.

Kode ASCII adalah kode 7-bit sedangkan EBCDIC adalah kode 8-bit. Kode ASCII lebih umum digunakan di seluruh dunia sementara EBCDIC digunakan terutama di komputer IBM yang besar.

Kode Kesalahan

Ada teknik kode biner yang tersedia untuk mendeteksi dan mengoreksi data selama transmisi data.

Kode Kesalahan	Deskripsi
Deteksi dan Koreksi Kesalahan	Deteksi kesalahan dan teknik kode koreksi

Ada banyak metode atau teknik yang dapat digunakan untuk mengubah kode dari satu format ke format lainnya. Kami akan mendemonstrasikan di sini berikut ini

• Konversi Biner ke BCD
• BCD ke Konversi Biner
• BCD ke Excess-3
• Excess-3 ke BCD

Konversi Biner ke BCD

Langkah

• Step 1 - Ubah bilangan biner menjadi desimal.

• Step 2 - Ubah angka desimal menjadi BCD.

Contoh - ubah (11101) ₂ ke BCD.

Langkah 1 - Ubah ke Desimal

Bilangan Biner - 11101 ₂

Menghitung Setara Desimal -

Langkah	Bilangan Biner	Angka desimal
Langkah 1	11101 2	((1 × 2 4 ) + (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 )) 10
Langkah 2	11101 2	(16 + 8 + 4 + 0 + 1) 10
LANGKAH 3	11101 2	29 10

Bilangan Biner - 11101 ₂ = Bilangan Desimal - 29 ₁₀

Langkah 2 - Ubah ke BCD

Angka Desimal - 29 ₁₀

Menghitung Setara BCD. Ubah setiap digit menjadi kelompok yang setara dengan empat digit biner.

Langkah	Angka desimal	Konversi
Langkah 1	29 10	0010 2 1001 2
Langkah 2	29 10	00101001 BCD

Hasil

(11101)2 =  (00101001)BCD

BCD ke Konversi Biner

Langkah

• Step 1 - Ubah angka BCD menjadi desimal.

• Step 2 - Ubah desimal menjadi biner.

Contoh - ubah (00101001) _BCD ke Biner.

Langkah 1 - Ubah ke BCD

Nomor BCD - (00101001) _BCD

Menghitung Setara Desimal. Ubah setiap empat digit menjadi satu grup dan dapatkan desimal yang setara untuk setiap grup.

Langkah	Nomor BCD	Konversi
Langkah 1	(00101001) BCD	0010 2 1001 2
Langkah 2	(00101001) BCD	2 10 9 10
LANGKAH 3	(00101001) BCD	29 10

Nomor BCD - (00101001) _BCD = Nomor Desimal - 29 ₁₀

Langkah 2 - Ubah ke Biner

Menggunakan metode pembagian panjang untuk konversi desimal ke biner.

Angka Desimal - 29 ₁₀

Menghitung Setara Biner -

Langkah	Operasi	Hasil	Sisa
Langkah 1	29/2	14	1
Langkah 2	14/2	7	0
LANGKAH 3	7/2	3	1
LANGKAH 4	3/2	1	1
LANGKAH 5	1/2	0	1

Seperti yang disebutkan pada Langkah 2 dan 4, sisa harus disusun dalam urutan terbalik sehingga sisa pertama menjadi digit paling signifikan (LSD) dan sisa terakhir menjadi digit paling signifikan (MSD).

Bilangan Desimal - 29 ₁₀ = Bilangan Biner - 11101 ₂

Hasil

(00101001)BCD = (11101)2

BCD ke Excess-3

Langkah

• Step 1 - Ubah BCD menjadi desimal.

• Step 2- Tambahkan (3) ₁₀ ke angka desimal ini.

• Step 3 - Ubah menjadi biner untuk mendapatkan kelebihan kode-3.

Contoh - ubah (0110) _BCD ke Excess-3.

Langkah 1 - Ubah menjadi desimal

(0110) _BCD = 6 ₁₀

Langkah 2 - Tambahkan 3 ke desimal

(6) ₁₀ + (3) ₁₀ = (9) ₁₀

Langkah 3 - Ubah menjadi Kelebihan-3

(9) ₁₀ = (1001) ₂

Hasil

(0110)BCD = (1001)XS-3

Konversi Kelebihan-3 ke BCD

Langkah

• Step 1- Kurangi (0011) ₂ dari setiap 4 bit kelebihan-3 digit untuk mendapatkan kode BCD yang sesuai.

Contoh - ubah (10011010) _XS-3 ke BCD.

Given XS-3 number  = 1 0 0 1 1 0 1 0 
Subtract (0011)2   = 1 0 0 1 0 1 1 1
                    --------------------
               BCD = 0 1 1 0   0 1 1 1

Hasil

(10011010)XS-3 = (01100111)BCD

Pelengkap digunakan dalam komputer digital untuk menyederhanakan operasi pengurangan dan untuk manipulasi logika. Untuk setiap sistem radix-r (radix r mewakili basis sistem bilangan) ada dua jenis komplemen.

SN	Melengkapi	Deskripsi
1	Pelengkap Radix	Komplemen radix disebut sebagai komplemen r
2	Pelengkap Radix yang Dikurangi	Komplemen radix yang berkurang disebut sebagai komplemen (r-1)

Pelengkap sistem biner

Karena sistem biner memiliki basis r = 2. Jadi dua jenis komplemen untuk sistem biner adalah komplemen 2 dan komplemen 1.

Pelengkap 1

Komplemen 1 dari sebuah angka ditemukan dengan mengubah semua 1 menjadi 0 dan semua 0 menjadi 1. Ini disebut mengambil komplemen atau komplemen 1. Contoh Pelengkap 1 adalah sebagai berikut.

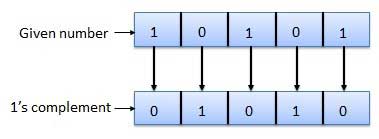
2 pelengkap

Komplemen bilangan biner 2 diperoleh dengan menambahkan 1 ke Least Significant Bit (LSB) dari 1 komplemen bilangan tersebut.

Komplemen 2 = komplemen 1 + 1

Contoh Pengimbang 2 adalah sebagai berikut.

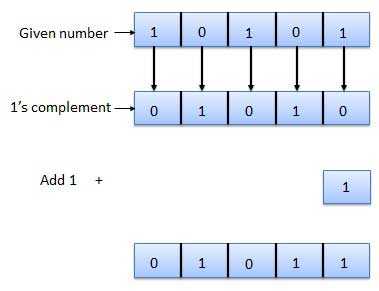
Aritmatika biner adalah bagian penting dari semua komputer digital dan banyak sistem digital lainnya.

Penambahan Biner

Ini adalah kunci untuk pengurangan biner, perkalian, pembagian. Ada empat aturan penjumlahan biner.

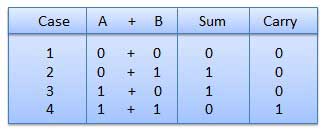
Dalam kasus keempat, penjumlahan biner menghasilkan jumlah (1 + 1 = 10) yaitu 0 ditulis di kolom yang ditentukan dan membawa 1 ke kolom berikutnya.

Contoh - Penambahan

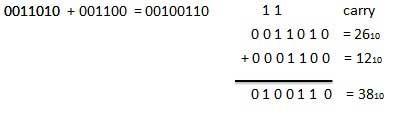
Pengurangan Biner

Subtraction and Borrow, kedua kata ini akan sangat sering digunakan untuk pengurangan biner. Ada empat aturan pengurangan biner.

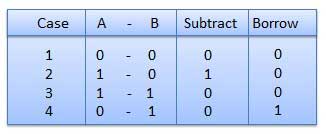
Contoh - Pengurangan

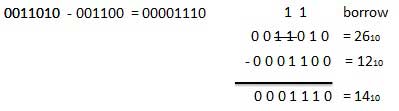
Perkalian Biner

Perkalian biner mirip dengan perkalian desimal. Ini lebih sederhana daripada perkalian desimal karena hanya 0 dan 1 yang terlibat. Ada empat aturan perkalian biner.

Contoh - Perkalian

Divisi Biner

Pembagian biner mirip dengan pembagian desimal. Ini disebut sebagai prosedur pembagian panjang.

Contoh - Divisi

Sistem Angka Oktal

Berikut adalah ciri-ciri sistem bilangan oktal.

• Menggunakan delapan digit, 0,1,2,3,4,5,6,7.

• Juga disebut sistem bilangan basis 8.

• Setiap posisi dalam bilangan oktal mewakili pangkat 0 dari basis (8). Contoh: 8 ⁰

• Posisi terakhir dalam bilangan oktal mewakili pangkat x dari alas (8). Contoh: 8 ^x dimana x mewakili posisi terakhir - 1.

Contoh

Nomor Oktal - 12570 ₈

Menghitung Setara Desimal -

Langkah	Nomor Oktal	Angka desimal
Langkah 1	12570 8	((1 × 8 4 ) + (2 × 8 3 ) + (5 × 8 2 ) + (7 × 8 1 ) + (0 × 8 0 )) 10
Langkah 2	12570 8	(4096 + 1024 + 320 + 56 + 0) 10
LANGKAH 3	12570 8	5496 10

Note −12570 ₈ biasanya ditulis sebagai 12570.

Penambahan Oktal

Tabel penjumlahan oktal berikut akan membantu Anda menangani penjumlahan oktal.

Untuk menggunakan tabel ini, cukup ikuti petunjuk yang digunakan dalam contoh ini: Tambahkan 6 ₈ dan 5 ₈ . Cari 6 di kolom A lalu cari 5 di kolom B. Titik di area 'jumlah' di mana kedua kolom ini berpotongan adalah 'jumlah' dari dua angka.

68 + 58 = 138.

Contoh - Penambahan

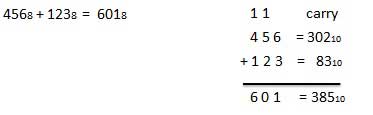
Pengurangan Oktal

Pengurangan bilangan oktal mengikuti aturan yang sama seperti pengurangan bilangan dalam sistem bilangan lainnya. Variasi satu-satunya adalah nomor pinjaman. Dalam sistem desimal, Anda meminjam sekelompok 10 ₁₀ . Dalam sistem biner, Anda meminjam sekelompok 2 ₁₀ . Dalam sistem oktal Anda meminjam sekelompok 8 ₁₀ .

Contoh - Pengurangan

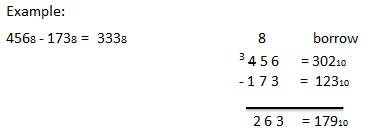
Sistem Angka Heksadesimal

Berikut adalah ciri-ciri sistem bilangan heksadesimal.

• Menggunakan 10 digit dan 6 huruf, 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F.

• Huruf mewakili angka mulai dari 10. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.

• Juga disebut sistem bilangan basis 16.

• Setiap posisi dalam bilangan heksadesimal mewakili pangkat 0 dari basis (16). Contoh - 16 ⁰

• Posisi terakhir dalam bilangan heksadesimal mewakili pangkat x dari basis (16). Contoh - 16 ^{x di} mana x mewakili posisi terakhir - 1.

Contoh

Bilangan Heksadesimal - 19FDE ₁₆

Menghitung Setara Desimal -

Langkah	Bilangan Heksadesimal	Angka desimal
Langkah 1	19FDE 16	((1 × 16 4 ) + (9 × 16 3 ) + (F × 16 2 ) + (D × 16 1 ) + (E × 16 0 )) 10
Langkah 2	19FDE 16	((1 × 16 4 ) + (9 × 16 3 ) + (15 × 16 2 ) + (13 × 16 1 ) + (14 × 16 0 )) 10
LANGKAH 3	19FDE 16	(65536 + 36864 + 3840 + 208 + 14) 10
LANGKAH 4	19FDE 16	106462 10

Note −19FDE ₁₆ biasanya ditulis sebagai 19FDE.

Penambahan Heksadesimal

Tabel penjumlahan heksadesimal berikut akan sangat membantu Anda menangani penjumlahan heksadesimal.

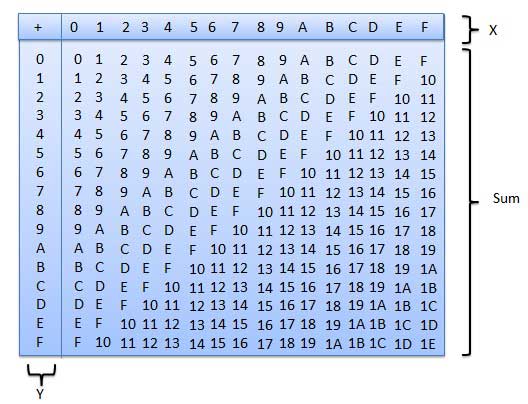
Untuk menggunakan tabel ini, cukup ikuti petunjuk yang digunakan dalam contoh ini - Tambahkan A ₁₆ dan 5 ₁₆ . Cari A di kolom X lalu cari angka 5 di kolom Y. Titik di area 'jumlah' tempat kedua kolom ini berpotongan adalah jumlah dari dua angka.

A16 + 516 = F16.

Contoh - Penambahan

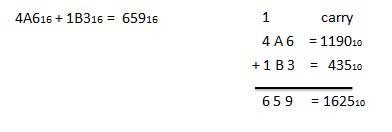
Pengurangan Heksadesimal

Pengurangan bilangan heksadesimal mengikuti aturan yang sama seperti pengurangan bilangan dalam sistem bilangan lainnya. Variasi satu-satunya adalah nomor pinjaman. Dalam sistem desimal, Anda meminjam sekelompok 10 ₁₀ . Dalam sistem biner, Anda meminjam sekelompok 2 ₁₀ . Dalam sistem heksadesimal Anda meminjam sekelompok 16 ₁₀ .

Contoh - Pengurangan

Aljabar Boolean digunakan untuk menganalisis dan menyederhanakan rangkaian digital (logika). Ia hanya menggunakan bilangan biner yaitu 0 dan 1. Disebut juga sebagaiBinary Algebra atau logical Algebra. Aljabar Boolean ditemukan olehGeorge Boole pada tahun 1854.

Aturan dalam Aljabar Boolean

Berikut adalah aturan penting yang digunakan dalam aljabar Boolean.

• Variabel yang digunakan hanya dapat memiliki dua nilai. Biner 1 untuk TINGGI dan Biner 0 untuk RENDAH.

• Komplemen variabel diwakili oleh sebuah overbar (-). Jadi, pelengkap variabel B direpresentasikan sebagai

  
  . Jadi jika B = 0 maka
  
  = 1 dan B = 1 maka
  
  = 0.

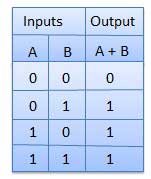
• ORing variabel diwakili oleh tanda plus (+) di antara mereka. Misalnya ORing dari A, B, C direpresentasikan sebagai A + B + C.

• ANDing logis dari dua atau lebih variabel diwakili dengan menulis titik di antara mereka seperti ABC Terkadang titik dapat dihilangkan seperti ABC.

Hukum Boolean

Ada enam jenis Hukum Boolean.

Hukum komutatif

Setiap operasi biner yang memenuhi ekspresi berikut ini disebut sebagai operasi komutatif.

Hukum komutatif menyatakan bahwa mengubah urutan variabel tidak berpengaruh pada keluaran rangkaian logika.

Hukum asosiatif

Hukum ini menyatakan bahwa urutan operasi logika dilakukan tidak relevan karena efeknya sama.

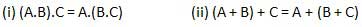
Hukum distributif

Hukum distributif menyatakan kondisi berikut.

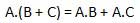
DAN hukum

Hukum ini menggunakan operasi AND. Oleh karena itu mereka disebut sebagaiAND hukum.

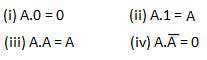
ATAU hukum

Hukum ini menggunakan operasi OR. Oleh karena itu mereka disebut sebagaiOR hukum.

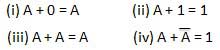
Hukum INVERSION

Hukum ini menggunakan operasi NOT. Hukum inversi menyatakan bahwa inversi ganda suatu variabel menghasilkan variabel asli itu sendiri.

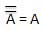
Teorema Boolean Penting

Berikut adalah beberapa Teorema Boolean yang penting.

Fungsi / teorema Boolean	Deskripsi
Fungsi Boolean	Fungsi dan Ekspresi Boolean, K-Map dan realisasi NAND Gates
Teorema De Morgan	Teorema 1 De Morgan dan Teorema 2

Gerbang logika adalah blok bangunan dasar dari sistem digital apa pun. Ini adalah rangkaian elektronik yang memiliki satu atau lebih dari satu masukan dan hanya satu keluaran. Hubungan antara input dan output didasarkan pada acertain logic. Berdasarkan ini, gerbang logika dinamai sebagai gerbang AND, gerbang OR, gerbang NOT dll.

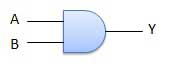
DAN Gerbang

Sirkuit yang melakukan operasi AND ditunjukkan pada gambar. Ini memiliki n masukan (n> = 2) dan satu keluaran.

Diagram logika

Meja kebenaran

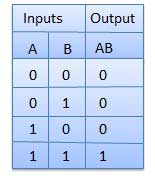
OR Gerbang

Sirkuit yang melakukan operasi OR ditunjukkan pada gambar. Ini memiliki n masukan (n> = 2) dan satu keluaran.

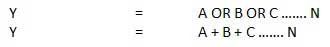
Diagram logika

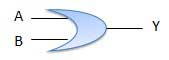
Meja kebenaran

BUKAN Gerbang

Gerbang NOT juga dikenal sebagai Inverter. Ini memiliki satu masukan A dan satu keluaran Y.

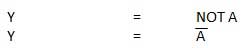
Diagram logika

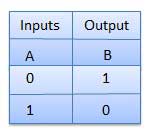
Meja kebenaran

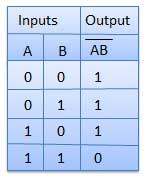
Gerbang NAND

Operasi NOT-AND dikenal sebagai operasi NAND. Ini memiliki n masukan (n> = 2) dan satu keluaran.

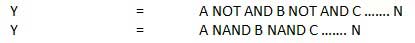
Diagram logika

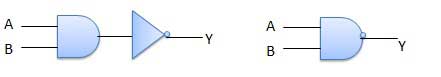
Meja kebenaran

Gerbang NOR

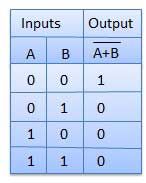
Operasi NOT-OR dikenal sebagai operasi NOR. Ini memiliki n masukan (n> = 2) dan satu keluaran.

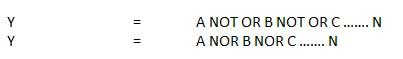
Diagram logika

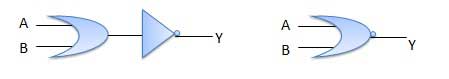
Meja kebenaran

Gerbang XOR

Gerbang XOR atau Ex-OR adalah jenis gerbang khusus. Ini dapat digunakan dalam penjumlahan setengah, penambah penuh dan pengurangan. Gerbang OR-eksklusif disingkat sebagai gerbang EX-OR atau kadang-kadang sebagai gerbang X-OR. Ini memiliki n masukan (n> = 2) dan satu keluaran.

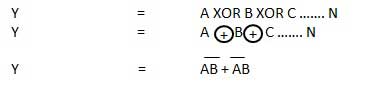
Diagram logika

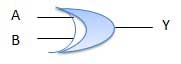
Meja kebenaran

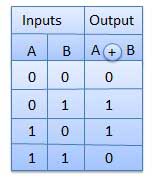
Gerbang XNOR

Gerbang XNOR adalah jenis gerbang khusus. Ini dapat digunakan dalam penjumlahan setengah, penambah penuh dan pengurangan. Gerbang eksklusif-NOR disingkat gerbang EX-NOR atau kadang-kadang sebagai gerbang X-NOR. Ini memiliki n masukan (n> = 2) dan satu keluaran.

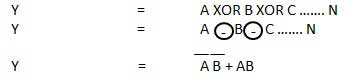
Diagram logika

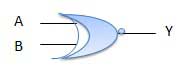
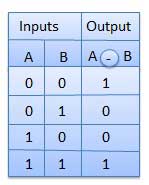
Meja kebenaran

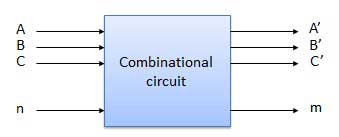
Rangkaian kombinasional adalah rangkaian yang di dalamnya kita menggabungkan gerbang-gerbang yang berbeda pada rangkaian tersebut, misalnya encoder, decoder, multiplexer dan demultiplexer. Beberapa karakteristik rangkaian kombinasional adalah sebagai berikut -

• Output dari rangkaian kombinasional setiap saat, hanya bergantung pada level yang ada di terminal input.

• Sirkuit kombinasional tidak menggunakan memori apa pun. Keadaan masukan sebelumnya tidak berpengaruh pada keadaan rangkaian saat ini.

• Sirkuit kombinasional dapat memiliki sejumlah n masukan dan m jumlah keluaran.

Diagram blok

Kami akan menguraikan beberapa sirkuit kombinasional penting sebagai berikut.

Half Adder

Half adder adalah rangkaian logika kombinasional dengan dua masukan dan dua keluaran. Sirkuit setengah penambah dirancang untuk menambahkan dua bit tunggal bilangan biner A dan B.Ini adalah blok bangunan dasar untuk penjumlahan dua bit tunggal.singlenomor bit. Sirkuit ini memiliki dua keluarancarry dan sum.

Diagram blok

Meja kebenaran

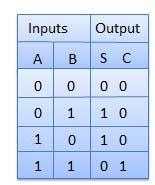
Diagram Sirkuit

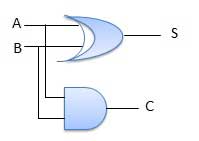
Adder penuh

Full adder dikembangkan untuk mengatasi kekurangan sirkuit Half Adder. Itu dapat menambahkan dua angka satu-bit A dan B, dan membawa c. Penambah penuh adalah rangkaian kombinasional tiga masukan dan dua keluaran.

Diagram blok

Meja kebenaran

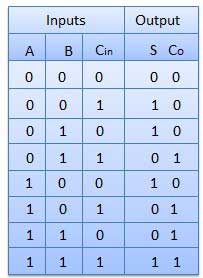
Diagram Sirkuit

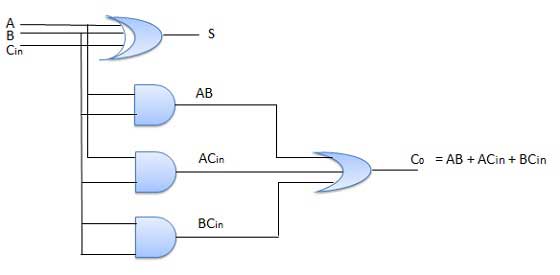
N-Bit Parallel Adder

Full Adder hanya mampu menambahkan dua digit angka biner bersama dengan input pembawa. Namun dalam prakteknya kita perlu menambahkan bilangan biner yang lebih panjang dari hanya satu bit. Untuk menambahkan dua bilangan biner n-bit kita perlu menggunakan penambah paralel n-bit. Ini menggunakan sejumlah penambah penuh di kaskade. Output carry dari penambah penuh sebelumnya terhubung untuk membawa masukan dari penambah penuh berikutnya.

4 Bit Parallel Adder

Dalam diagram blok, A ₀ dan B ₀ mewakili LSB dari empat bit word A dan B. Oleh karena itu, Full Adder-0 adalah tahap terendah. Oleh karena itu C _in-nya telah dibuat secara permanen 0. Sisa dari koneksi yang sama persis dengan n-bit parallel adder ditunjukkan pada gambar. Penambah paralel empat bit adalah rangkaian logika yang sangat umum.

Diagram blok

Pengurang Paralel N-Bit

Pengurangan dapat dilakukan dengan mengambil komplemen 1 atau 2 dari bilangan yang akan dikurangi. Misalnya kita bisa melakukan pengurangan (AB) dengan menambahkan komplemen 1 atau 2 dari B ke A. Itu berarti kita bisa menggunakan penjumlah biner untuk melakukan pengurangan biner.

Pengurang Paralel 4 Bit

Bilangan yang akan dikurangi (B) pertama-tama dilewatkan melalui inverter untuk mendapatkan komplemen 1-nya. Penambah 4-bit kemudian menambahkan komplemen A dan 2 dari B untuk menghasilkan pengurangan. S ₃ S ₂ S ₁ S ₀ merepresentasikan hasil pengurangan biner (AB) dan carry output C _out merepresentasikan polaritas hasil. Jika A> B maka Cout = 0 dan hasilnya berupa biner (AB) maka C _out = 1 dan hasilnya berupa komplemen 2.

Diagram blok

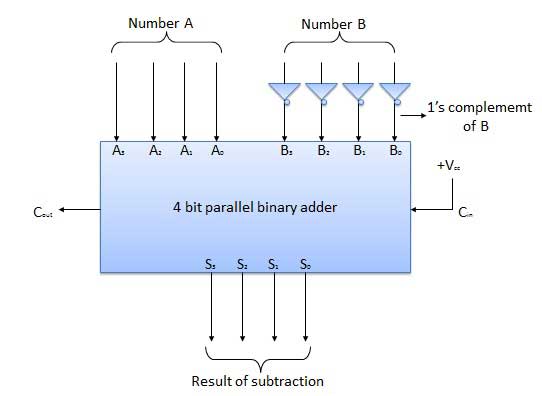
Pengurang Setengah

Half subtractor adalah rangkaian kombinasi dengan dua masukan dan dua keluaran (selisih dan pinjam). Ini menghasilkan perbedaan antara dua bit biner pada input dan juga menghasilkan output (Pinjam) untuk menunjukkan apakah 1 telah dipinjam. Dalam pengurangan (AB), A disebut sebagai bit Minuend dan B disebut sebagai bit Subtrahend.

Meja kebenaran

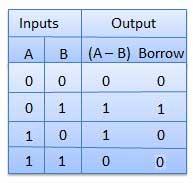
Diagram Sirkuit

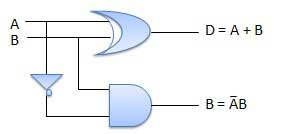
Pengurang Penuh

Kerugian dari pengurang setengah diatasi dengan pengurang penuh. Pengurang penuh adalah rangkaian kombinasional dengan tiga masukan A, B, C dan dua keluaran D dan C '. A adalah 'minuend', B adalah 'subtrahend', C adalah 'pinjaman' yang dihasilkan oleh tahap sebelumnya, D adalah keluaran selisih dan C 'adalah keluaran pinjaman.

Meja kebenaran

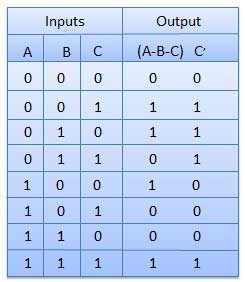
Diagram Sirkuit

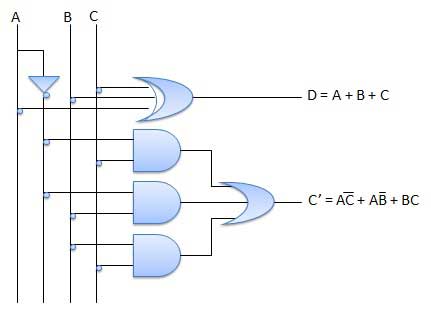
Multiplexer

Multiplexer adalah jenis sirkuit kombinasional khusus. Ada input n-data, satu output dan m pilih input dengan 2m = n. Ini adalah rangkaian digital yang memilih salah satu dari n masukan data dan mengarahkannya ke keluaran. Pemilihan salah satu input n dilakukan oleh input terpilih. Tergantung pada kode digital yang diterapkan pada input yang dipilih, satu dari n sumber data dipilih dan dikirimkan ke output tunggal Y. E disebut strobe atau mengaktifkan input yang berguna untuk cascading. Ini umumnya merupakan terminal rendah aktif yang berarti ia akan melakukan operasi yang diperlukan saat rendah.

Diagram blok

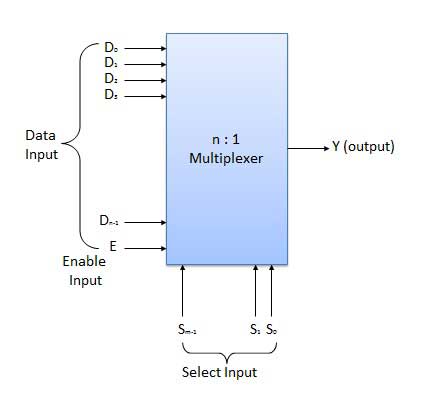
Multiplexer tersedia dalam berbagai variasi

• Multiplexer 2: 1
• Multiplexer 4: 1
• Multiplekser 16: 1
• 32: 1 multiplexer

Diagram Blok

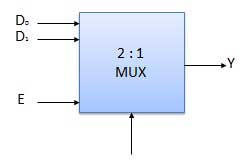
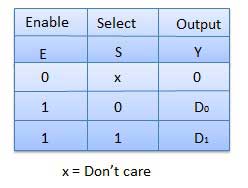
Meja kebenaran

Demultiplexer

Demultiplexer melakukan operasi kebalikan dari multiplexer yaitu menerima satu input dan mendistribusikannya ke beberapa output. Ini hanya memiliki satu masukan, n keluaran, m masukan pilih. Pada satu waktu, hanya satu jalur keluaran yang dipilih oleh jalur terpilih dan masukan ditransmisikan ke jalur keluaran yang dipilih. De-multiplexer setara dengan sakelar multi arah kutub tunggal seperti yang ditunjukkan pada gambar.

Demultiplexer hadir dalam berbagai variasi.

• Demultiplexer 1: 2
• Demultiplexer 1: 4
• 1: 16 demultiplexer
• 1: 32 demultiplexer

Diagram blok

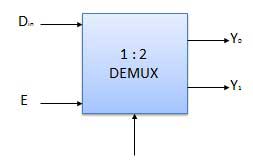
Meja kebenaran

Dekoder

Dekoder adalah sirkuit kombinasional. Ini memiliki n masukan dan maksimum m = 2n keluaran. Decoder identik dengan demultiplexer tanpa input data apa pun. Ini melakukan operasi yang berlawanan dengan encoder.

Diagram blok

Contoh Decoder berikut.

• Pengonversi kode
• Dekoder BCD ke tujuh segmen
• Dekoder tabung Nixie
• Aktuator relai

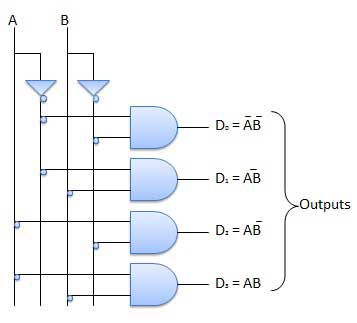
2 hingga 4 Baris Decoder

Diagram blok dari 2 hingga 4 baris decoder ditunjukkan pada gambar. A dan B adalah dua masukan di mana D hingga D adalah empat keluaran. Tabel kebenaran menjelaskan operasi decoder. Ini menunjukkan bahwa setiap output adalah 1 hanya untuk kombinasi input tertentu.

Diagram blok

Meja kebenaran

Sirkuit Logika

Pembuat enkode

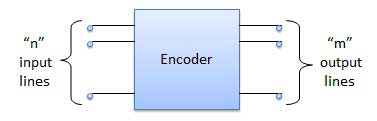
Encoder adalah rangkaian kombinasional yang dirancang untuk melakukan operasi kebalikan dari decoder. Encoder memiliki n jumlah baris input dan m jumlah baris output. Encoder menghasilkan kode biner m bit yang sesuai dengan nomor input digital. Encoder menerima input n kata digital dan mengubahnya menjadi m bit kata digital lain.

Diagram blok

Contoh Encoder berikut.

• Encoder prioritas
• Desimal ke encoder BCD
• Oktal ke encoder biner
• Heksadesimal ke pembuat enkode biner

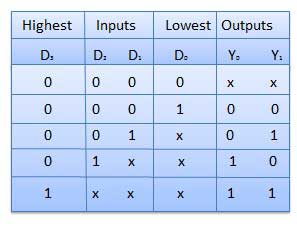
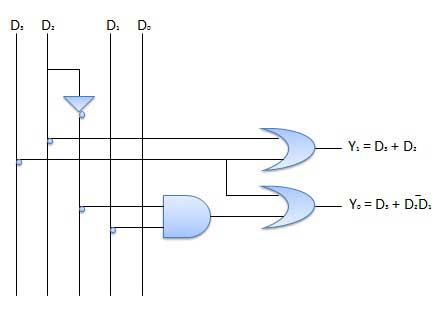
Encoder Prioritas

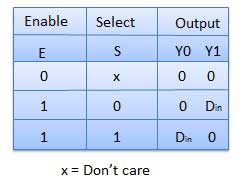
Ini adalah jenis encoder khusus. Prioritas diberikan ke jalur masukan. Jika dua atau lebih jalur input adalah 1 pada saat yang sama, maka jalur input dengan prioritas tertinggi akan dipertimbangkan. Ada empat input D ₀ , D ₁ , D ₂ , D ₃ dan dua output Y ₀ , Y ₁ . Dari keempat masukan D ₃ memiliki prioritas tertinggi dan D ₀ memiliki prioritas terendah. Itu berarti jika D ₃ = 1 maka Y ₁ Y ₁ = 11 terlepas dari input lainnya. Demikian pula jika D ₃ = 0 dan D ₂ = 1 maka Y ₁ Y ₀ = 10 terlepas dari input lainnya.

Diagram blok

Meja kebenaran

Sirkuit Logika

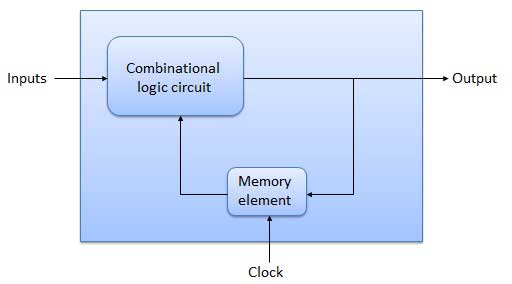
Sirkuit kombinasional tidak menggunakan memori apa pun. Oleh karena itu keadaan input sebelumnya tidak berpengaruh pada keadaan rangkaian saat ini. Tetapi rangkaian sekuensial memiliki memori sehingga keluaran dapat bervariasi berdasarkan masukan. Jenis sirkuit ini menggunakan input, output, clock, dan elemen memori sebelumnya.

Diagram blok

Flip Flop

Flip flop adalah rangkaian sekuensial yang umumnya mengambil sampel inputnya dan mengubah outputnya hanya pada waktu tertentu dan tidak terus menerus. Flip flop dikatakan sensitif tepi atau edge triggered daripada level trigger seperti kait.

SR Flip Flop

Ini pada dasarnya adalah kait SR menggunakan gerbang NAND dengan tambahan enablememasukkan. Ini juga disebut sebagai SR-FF yang dipicu level. Untuk ini, rangkaian keluaran akan berlangsung jika dan hanya jika masukan pengaktifan (E) diaktifkan. Singkatnya rangkaian ini akan beroperasi sebagai pengunci SR jika E = 1 tetapi tidak ada perubahan pada keluaran jika E = 0.

Diagram Blok

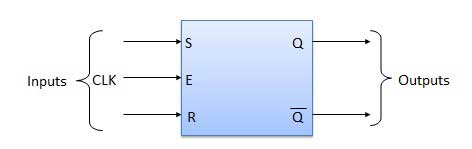
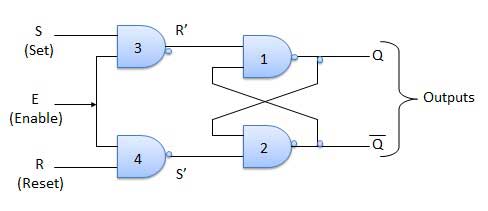
Diagram Sirkuit

Meja kebenaran

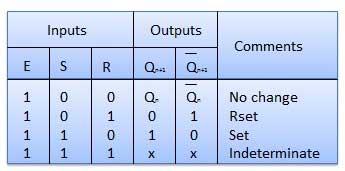
Operasi

SN	Kondisi	Operasi
1	S = R = 0 : No change	Jika S = R = 0 maka keluaran gerbang NAND 3 dan 4 dipaksa menjadi 1. Karenanya R 'dan S' keduanya akan sama dengan 1. Karena S 'dan R' adalah input dari kait SR dasar menggunakan gerbang NAND, tidak akan ada perubahan dalam status output.
2	S = 0, R = 1, E = 1	Karena S = 0, keluaran NAND-3 yaitu R '= 1 dan E = 1 keluaran NAND-4 yaitu S' = 0. Maka Q n + 1 = 0 dan Q n + 1 bar = 1. Ini adalah kondisi reset.
3	S = 1, R = 0, E = 1	Output dari NAND-3 yaitu R '= 0 dan output NAND-4 yaitu S' = 1. Oleh karena itu output dari kait SR NAND adalah Q n + 1 = 1 dan Q n + 1 bar = 0. Ini adalah kondisi reset.
4	S = 1, R = 1, E = 1	Karena S = 1, R = 1 dan E = 1, output dari gerbang NAND 3 dan 4 keduanya adalah 0 yaitu S '= R' = 0. Oleh karena itu Race kondisi akan terjadi di kait NAND dasar.

Master Slave JK Flip Flop

Master slave JK FF adalah kaskade dua SR FF dengan umpan balik dari keluaran kedua ke masukan pertama. Guru adalah tingkat positif yang dipicu. Tetapi karena kehadiran inverter di garis jam, budak akan merespons level negatif. Karenanya ketika jam = 1 (level positif) master aktif dan budak tidak aktif. Sedangkan saat clock = 0 (level rendah) slave aktif dan master tidak aktif.

Diagram Sirkuit

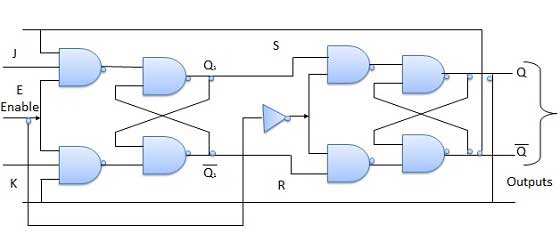
Meja kebenaran

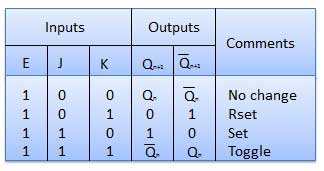
Operasi

SN	Kondisi	Operasi
1	J = K = 0 (No change)	Ketika clock = 0, budak menjadi aktif dan master tidak aktif. Tetapi karena input S dan R tidak berubah, output slave juga tidak akan berubah. Oleh karena itu, keluaran tidak akan berubah jika J = K = 0.
2	J = 0 and K = 1 (Reset)	Jam = 1 - Master aktif, budak tidak aktif. Oleh karena itu keluaran dari master menjadi Q 1 = 0 dan Q 1 bar = 1. Artinya S = 0 dan R = 1. Jam = 0 - Budak aktif, master tidak aktif. Oleh karena itu, keluaran dari slave menjadi Q = 0 dan Q bar = 1. Lagi jam = 1 - Master aktif, budak tidak aktif. Oleh karena itu, meskipun dengan perubahan keluaran Q = 0 dan Q bar = 1 diumpankan kembali ke master, keluarannya akan menjadi Q1 = 0 dan Q1 bar = 1. Itu berarti S = 0 dan R = 1. Oleh karena itu dengan clock = 0 dan slave menjadi aktif, output slave akan tetap Q = 0 dan Q bar = 1. Jadi kita mendapatkan output yang stabil dari Master slave.
3	J = 1 and K = 0 (Set)	Jam = 1 - Master aktif, budak tidak aktif. Oleh karena itu keluaran dari master menjadi Q 1 = 1 dan Q 1 bar = 0. Artinya S = 1 dan R = 0. Jam = 0 - Budak aktif, master tidak aktif. Oleh karena itu, keluaran dari slave menjadi Q = 1 dan Q bar = 0. Sekali lagi clock = 1 - maka dapat ditunjukkan bahwa output slave distabilkan ke Q = 1 dan Q bar = 0.
4	J = K = 1 (Toggle)	Jam = 1 - Master aktif, budak tidak aktif. Keluaran master akan diubah. Jadi S dan R juga akan dibalik. Jam = 0 - Budak aktif, master tidak aktif. Keluaran budak akan berubah. Output yang diubah ini dikembalikan ke input master. Tetapi karena clock = 0, master masih tidak aktif. Jadi itu tidak menanggapi keluaran yang diubah ini. Ini untuk menghindari beberapa toggling yang mengarah pada kondisi balapan di sekitar. Master slave flip flop akan menghindari kondisi balapan di sekitar.

Penundaan Flip Flop / D Flip Flop

Delay Flip Flop atau D Flip Flop adalah kait SR berpagar sederhana dengan inverter NAND terhubung antara input S dan R. Ini hanya memiliki satu masukan. Data masukan muncul pada keluaran setelah beberapa waktu. Karena adanya delay data antara i / p dan o / p ini disebut delay flip flop. S dan R akan menjadi pelengkap satu sama lain karena inverter NAND. Maka S = R = 0 atau S = R = 1, kondisi input ini tidak akan pernah muncul. Masalah ini dicegah dengan kondisi SR = 00 dan SR = 1.

Diagram Blok

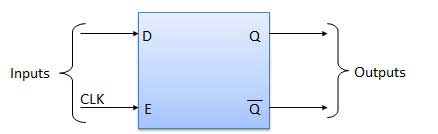
Diagram Sirkuit

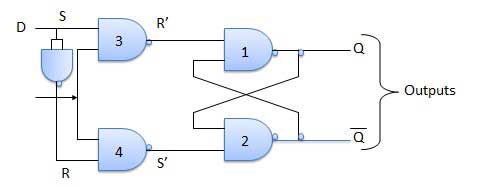
Meja kebenaran

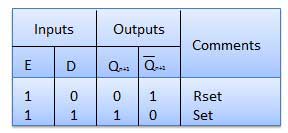
Operasi

SN	Kondisi	Operasi
1	E = 0	Latch dinonaktifkan. Karenanya tidak ada perubahan output.
2	E = 1 and D = 0	Jika E = 1 dan D = 0 maka S = 0 dan R = 1. Oleh karena itu, terlepas dari keadaan sekarang, keadaan selanjutnya adalah Q n + 1 = 0 dan Q n + 1 bar = 1. Ini adalah kondisi reset.
3	E = 1 and D = 1	Jika E = 1 dan D = 1, maka S = 1 dan R = 0. Ini akan mengatur latch dan Q n + 1 = 1 dan Q n + 1 bar = 0 terlepas dari keadaan saat ini.

Toggle Flip Flop / T Flip Flop

Toggle flip flop pada dasarnya adalah JK flip flop dengan terminal J dan K yang terhubung secara permanen. Ini hanya memiliki masukan yang dilambangkan denganTseperti yang ditunjukkan pada Diagram Simbol. Simbol untuk T flip flop yang dipicu oleh tepi positif ditunjukkan pada Diagram Blok.

Diagram Simbol

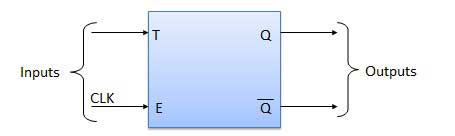
Diagram Blok

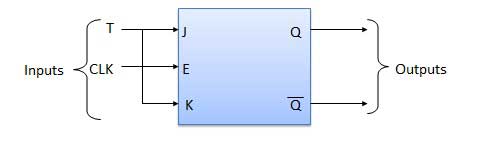
Meja kebenaran

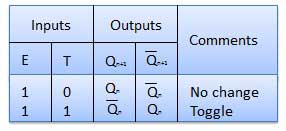
Operasi

SN	Kondisi	Operasi
1	T = 0, J = K = 0	Output Q dan Q bar tidak akan berubah
2	T = 1, J = K = 1	Output akan beralih sesuai dengan setiap tepi depan sinyal clock.

Flip-flop adalah sel memori 1 bit yang dapat digunakan untuk menyimpan data digital. Untuk meningkatkan kapasitas penyimpanan dalam hal jumlah bit, kita harus menggunakan kelompok flip-flop. Kelompok flip-flop seperti itu dikenal sebagai aRegister. Itun-bit register akan terdiri dari n jumlah flip-flop dan mampu menyimpan file n-bit kata.

Data biner dalam register dapat dipindahkan dalam register dari satu flip-flop ke flip-flop lainnya. Register yang memungkinkan transfer data tersebut disebut sebagaishift registers. Ada empat mode operasi register geser.

• Input Serial Output Serial
• Input Serial Output Paralel
• Output Serial Input Paralel
• Input Paralel Output Paralel

Input Serial Output Serial

Biarkan semua flip-flop awalnya dalam kondisi reset yaitu Q ₃ = Q ₂ = Q ₁ = Q ₀ = 0. Jika entri nomor biner empat bit 1 1 1 1 dibuat ke dalam register, nomor ini harus diaplikasikan keD_inbit dengan bit LSB diterapkan terlebih dahulu. Input D FF-3 yaitu D ₃ terhubung ke input data serialD_in. Output FF-3 yaitu Q ₃ dihubungkan ke input flip-flop berikutnya yaitu D ₂ dan seterusnya.

Diagram Blok

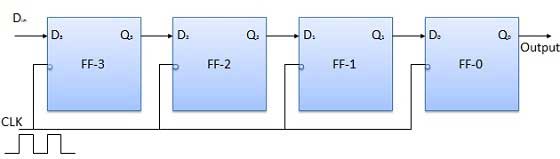
Operasi

Sebelum penerapan sinyal clock, biarkan Q ₃ Q ₂ Q ₁ Q ₀ = 0000 dan terapkan bit LSB dari nomor yang akan dimasukkan ke D _in . Jadi D _in = D ₃ = 1. Terapkan jam. Pada tepi jam jatuh pertama, FF-3 diatur, dan kata yang disimpan dalam register adalah Q ₃ Q ₂ Q ₁ Q ₀ = 1000.

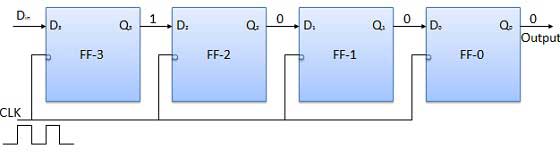
Terapkan bit berikutnya ke D _in . Jadi D _in = 1. Segera setelah tepi negatif jam berikutnya mengenai, FF-2 akan diatur dan kata yang disimpan berubah menjadi Q ₃ Q ₂ Q ₁ Q ₀ = 1100.

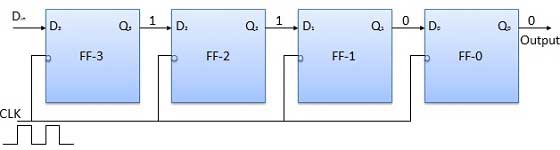
Terapkan bit berikutnya yang akan disimpan yaitu 1 ke D _in . Terapkan detak jam. Segera setelah clock edge negatif ketiga mengenai, FF-1 akan diatur dan output akan diubah ke Q ₃ Q ₂ Q ₁ Q ₀ = 1110.

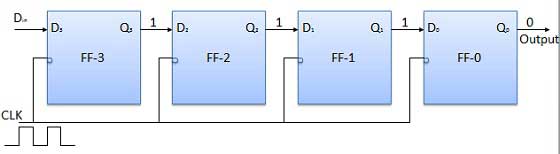
Demikian pula dengan D _in = 1 dan dengan clock edge negatif keempat tiba, kata yang disimpan dalam register adalah Q ₃ Q ₂ Q ₁ Q ₀ = 1111.

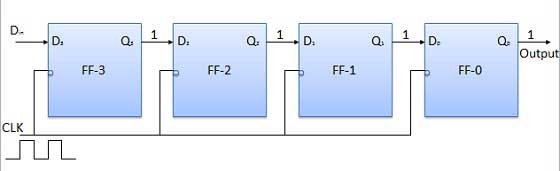
Meja kebenaran

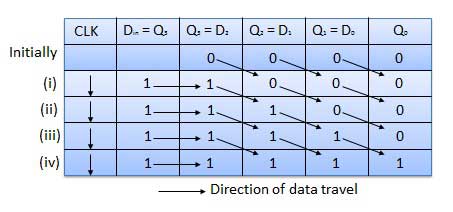
Bentuk gelombang

Input Serial Output Paralel

• Dalam jenis operasi seperti itu, data dimasukkan secara serial dan diambil secara paralel.

• Data dimuat sedikit demi sedikit. Keluaran dinonaktifkan selama data sedang dimuat.

• Segera setelah pemuatan data selesai, semua flip-flop berisi data yang diperlukan, keluaran diaktifkan sehingga semua data yang dimuat tersedia di semua jalur keluaran pada saat yang bersamaan.

• 4 siklus clock diperlukan untuk memuat kata empat bit. Oleh karena itu kecepatan pengoperasian mode SIPO sama dengan mode SISO.

Diagram Blok

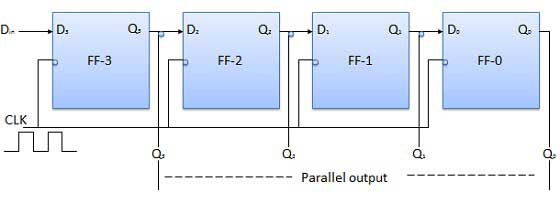
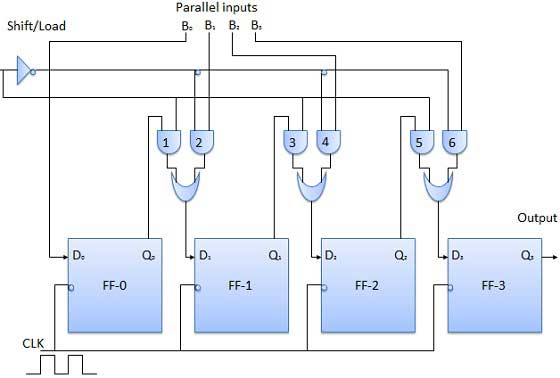
Output Serial Input Paralel (PISO)

• Bit data dimasukkan secara paralel.

• Sirkuit yang ditunjukkan di bawah ini adalah register output serial input paralel empat bit.

• Output dari Flip Flop sebelumnya dihubungkan dengan input berikutnya melalui rangkaian kombinasional.

• Kata masukan biner B ₀ , B ₁ , B ₂ , B ₃ diterapkan melalui rangkaian kombinasional yang sama.

• Ada dua mode di mana rangkaian ini dapat bekerja yaitu - mode shift atau mode beban.

Mode beban

Ketika garis shift / load bar rendah (0), gerbang AND 2, 4 dan 6 menjadi aktif mereka akan melewatkan bit B ₁ , B ₂ , B ₃ ke flip-flop yang sesuai. Di tepi jam yang rendah, input biner B ₀ , B ₁ , B ₂ , B ₃ akan dimuat ke dalam sandal jepit yang sesuai. Dengan demikian pembebanan paralel terjadi.

Mode shift

Ketika garis shift / load bar rendah (1), gerbang AND 2, 4 dan 6 menjadi tidak aktif. Oleh karena itu, pemuatan data secara paralel menjadi tidak mungkin. Tapi gerbang AND 1,3 dan 5 menjadi aktif. Oleh karena itu pergeseran data dari kiri ke kanan sedikit demi sedikit pada penerapan pulsa clock. Dengan demikian operasi paralel dalam serial keluar terjadi.

Diagram Blok

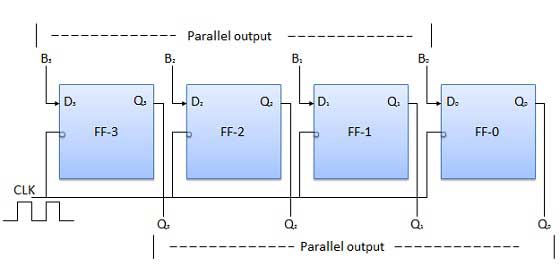
Parallel Input Parallel Output (PIPO)

Dalam mode ini, input biner 4 bit B ₀ , B ₁ , B ₂ , B ₃ diterapkan ke input data D ₀ , D ₁ , D ₂ , D ₃ masing-masing dari empat flip-flop. Segera setelah clock edge negatif diterapkan, bit biner input akan dimuat ke dalam flip-flop secara bersamaan. Bit yang dimuat akan muncul secara bersamaan ke sisi keluaran. Hanya pulsa clock yang penting untuk memuat semua bit.

Diagram Blok

Register Geser Dua Arah

• Jika bilangan biner digeser ke kiri dengan satu posisi maka itu setara dengan mengalikan bilangan asli dengan 2. Demikian pula jika bilangan biner digeser ke kanan dengan satu posisi maka itu setara dengan membagi bilangan asli dengan 2.

• Oleh karena itu, jika kita ingin menggunakan register geser untuk mengalikan dan membagi bilangan biner yang diberikan, maka kita harus dapat memindahkan data ke arah kiri atau kanan.

• Register seperti itu disebut register dua arah. Register geser dua arah empat bit ditunjukkan pada gambar.

• Ada dua input serial yaitu input data geser kanan serial DR, dan input data geser kiri serial bersama dengan input mode pilih (M).

Diagram Blok

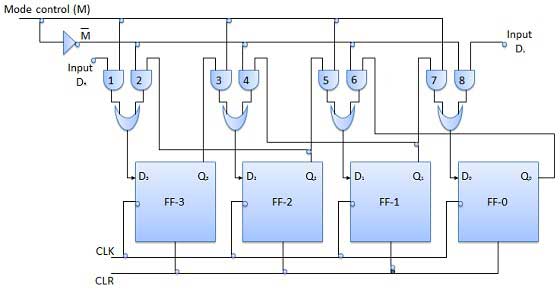
Operasi

SN	Kondisi	Operasi
1	With M = 1 − Shift right operation	Jika M = 1, maka gerbang AND 1, 3, 5 dan 7 diaktifkan sedangkan gerbang AND 2, 4, 6 dan 8 yang tersisa akan dinonaktifkan. Data di D R digeser ke kanan sedikit demi sedikit dari FF-3 ke FF-0 pada penerapan pulsa clock. Jadi dengan M = 1 kita mendapatkan operasi pergeseran kanan serial.
2	With M = 0 − Shift left operation	Ketika kontrol mode M terhubung ke 0 maka gerbang AND 2, 4, 6 dan 8 diaktifkan sementara 1, 3, 5 dan 7 dinonaktifkan. Data di DL bergeser ke kiri sedikit demi sedikit dari FF-0 ke FF-3 pada penerapan pulsa clock. Jadi dengan M = 0 kita mendapatkan operasi pergeseran kanan serial.

Register Geser Universal

Register geser yang dapat menggeser data hanya dalam satu arah disebut register geser uni-directional. Register geser yang dapat menggeser data ke dua arah disebut register geser dua arah. Menerapkan logika yang sama, register geser yang dapat menggeser data ke dua arah serta memuatnya secara paralel, dikenal sebagai register geser universal. Register geser mampu melakukan operasi berikut -

• Pembebanan paralel
• Pergeseran Kiri
• Pergeseran kanan

Input kontrol mode dihubungkan ke logika 1 untuk operasi pembebanan paralel sedangkan itu terhubung ke 0 untuk perpindahan serial. Dengan pin kontrol mode yang terhubung ke ground, register geser universal bertindak sebagai register dua arah. Untuk operasi kiri serial, input diterapkan ke input serial yang menuju ke gerbang AND-1 yang ditunjukkan pada gambar. Sedangkan untuk operasi shift kanan, input serial diterapkan ke input D.

Diagram Blok

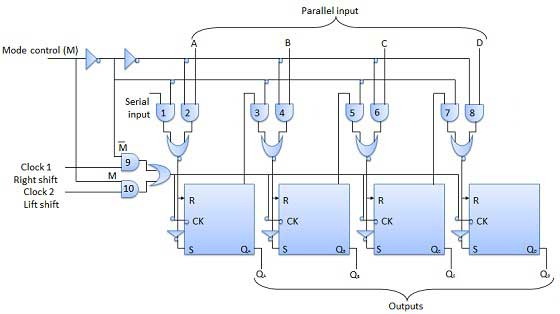
Penghitung adalah rangkaian sekuensial. Sirkuit digital yang digunakan untuk menghitung pulsa dikenal sebagai pencacah. Counter adalah aplikasi sandal jepit terluas. Ini adalah sekelompok sandal jepit dengan sinyal jam yang diterapkan. Penghitung terdiri dari dua jenis.

• Penghitung asinkron atau riak.
• Penghitung sinkron.

Penghitung asinkron atau riak

Diagram logika penghitung riak 2-bit ditunjukkan pada gambar. Tombol toggle (T) flip-flop sedang digunakan. Tetapi kita dapat menggunakan JK flip-flop juga dengan J dan K terhubung secara permanen ke logika 1. Clock eksternal diterapkan ke input clock dari flip-flop A dan output Q _A diterapkan ke input clock dari flip-flop berikutnya yaitu FF-B.

Diagram Logis

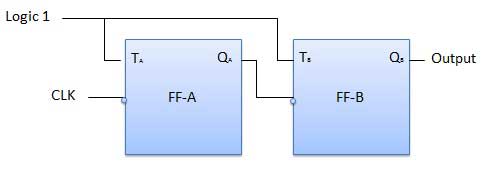
Operasi

SN	Kondisi	Operasi
1	Initially let both the FFs be in the reset state	Q B Q A = 00 awalnya
2	After 1st negative clock edge	Segera setelah tepi jam negatif pertama diterapkan, FF-A akan beralih dan Q A akan sama dengan 1. Q A terhubung ke input clock FF-B. Sejak Q A telah berubah dari 0 ke 1, itu diperlakukan sebagai clock edge positif oleh FF-B. Tidak ada perubahan di Q B karena FF-B adalah tepi negatif yang dipicu FF. Q B Q A = 01 setelah pulsa clock pertama.
3	After 2nd negative clock edge	Pada kedatangan tepi jam negatif kedua, FF-A beralih lagi dan Q A = 0. Perubahan Q A bertindak sebagai clock edge negatif untuk FF-B. Jadi itu juga akan beralih, dan Q B akan menjadi 1. Q B Q A = 10 setelah pulsa clock kedua.
4	After 3rd negative clock edge	Pada kedatangan tepi jam negatif ke-3, FF-A beralih lagi dan Q A menjadi 1 dari 0. Karena ini adalah perubahan positif yang sedang berlangsung, FF-B tidak meresponsnya dan tetap tidak aktif. Jadi Q B tidak berubah dan terus sama dengan 1. Q B Q A = 11 setelah pulsa clock ketiga.
5	After 4th negative clock edge	Pada kedatangan tepi jam negatif ke-4, FF-A beralih lagi dan Q A menjadi 1 dari 0. Perubahan negatif pada Q A ini bertindak sebagai pulsa clock untuk FF-B. Karenanya ia beralih untuk mengubah Q B dari 1 ke 0. Q B Q A = 00 setelah pulsa clock keempat.

Meja kebenaran

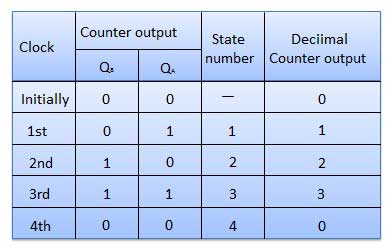
Penghitung sinkron

Jika pulsa "jam" diterapkan ke semua sandal jepit di penghitung secara bersamaan, maka penghitung seperti itu disebut pencacah sinkron.

Penghitung up sinkron 2-bit

Input J _A dan K _A dari FF-A terikat ke logika 1. Jadi FF-A akan bekerja sebagai toggle flip-flop. J _B dan K _B input yang terhubung ke Q _A .

Diagram Logis

Operasi

SN	Kondisi	Operasi
1	Initially let both the FFs be in the reset state	Q B Q A = 00 awalnya.
2	After 1st negative clock edge	Segera setelah tepi jam negatif pertama diterapkan, FF-A akan beralih dan Q A akan berubah dari 0 ke 1. Tetapi pada saat penerapan clock edge negatif, Q A , J B = K B = 0. Karenanya FF-B tidak akan berubah statusnya. Jadi Q B akan tetap 0. Q B Q A = 01 setelah pulsa clock pertama.
3	After 2nd negative clock edge	Pada kedatangan tepi jam negatif kedua, FF-A beralih lagi dan Q A berubah dari 1 menjadi 0. Tapi saat ini Q A adalah 1. Jadi J B = K B = 1 dan FF-B akan toggle. Karenanya Q B berubah dari 0 ke 1. Q B Q A = 10 setelah pulsa clock kedua.
4	After 3rd negative clock edge	Pada penerapan tepi jam jatuh ketiga, FF-A akan beralih dari 0 ke 1 tetapi tidak ada perubahan status untuk FF-B. Q B Q A = 11 setelah pulsa clock ketiga.
5	After 4th negative clock edge	Pada penerapan pulsa jam berikutnya, Q A akan berubah dari 1 menjadi 0 karena Q B juga akan berubah dari 1 ke 0. Q B Q A = 00 setelah pulsa clock keempat.

Klasifikasi penghitung

Bergantung pada cara penghitungan berlangsung, penghitung sinkron atau asinkron diklasifikasikan sebagai berikut -

• Penghitung naik
• Penghitung mundur
• Penghitung Atas / Bawah

Penghitung ATAS / BAWAH

Penghitung atas dan bawah digabungkan untuk mendapatkan penghitung ATAS / BAWAH. Input kontrol mode (M) juga disediakan untuk memilih mode naik atau turun. Sirkuit kombinasional harus dirancang dan digunakan di antara setiap pasang flip-flop untuk mencapai operasi naik / turun.

• Jenis penghitung naik / turun
• Penghitung riak ATAS / BAWAH
• Penghitung sinkron NAIK / TURUN

Penghitung Riak ATAS / BAWAH

Di penghitung riak ATAS / BAWAH semua FF beroperasi dalam mode sakelar. Jadi, baik sandal jepit T atau sandal jepit JK harus digunakan. Flip-flop LSB menerima jam secara langsung. Tetapi clock untuk setiap FF lainnya diperoleh dari (Q = Q bar) output dari FF sebelumnya.

• UP counting mode (M=0)- Output Q dari FF sebelumnya dihubungkan ke clock tahap berikutnya jika ingin menghitung naik. Untuk mode ini, input pemilihan mode M berada pada logika 0 (M = 0).

• DOWN counting mode (M=1)- Jika M = 1, maka output Q bar dari FF sebelumnya terhubung ke FF berikutnya. Ini akan mengoperasikan penghitung dalam mode penghitungan.

Contoh

Penghitung riak atas / bawah biner 3-bit.

• 3-bit - maka diperlukan tiga FF.

• ATAS / BAWAH - Jadi input kontrol mode sangat penting.

• Untuk penghitung riak, output Q dari FF sebelumnya dihubungkan ke input clock dari yang berikutnya.

• Untuk penghitung riak, output Q dari FF sebelumnya dihubungkan ke input clock dari yang berikutnya.

• Untuk penghitung riak ke bawah, output bilah Q dari FF sebelumnya terhubung ke input jam dari yang berikutnya.

• Biarkan pemilihan output batang Q dan Q dari FF sebelumnya dikontrol oleh input kontrol mode M sehingga, Jika M = 0, penghitungan UP. Jadi hubungkan Q ke CLK. Jika M = 1, Hitung TURUN. Jadi hubungkan Q bar ke CLK.

Diagram Blok

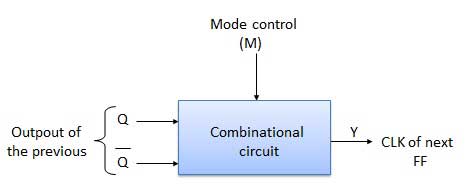
Meja kebenaran

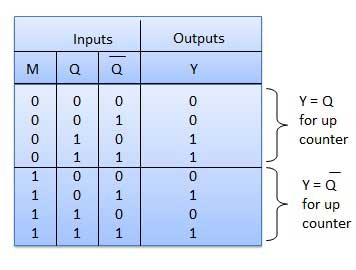
Operasi

SN	Kondisi	Operasi
1	Case 1 − With M = 0 (Up counting mode)	Jika M = 0 dan M bar = 1, maka AND gerbang 1 dan 3 dalam gbr. akan diaktifkan sedangkan gerbang AND 2 dan 4 akan dinonaktifkan. Oleh karena itu Q A akan terhubung ke input clock FF-B dan Q B terhubung ke input clock FF-C. Koneksi ini sama dengan koneksi untuk up counter normal. Jadi dengan M = 0 sirkuit bekerja sebagai penghitung naik.
2	Case 2: With M = 1 (Down counting mode)	Jika M = 1, maka AND gerbang 2 dan 4 dalam gbr. diaktifkan sedangkan gerbang AND 1 dan 3 dinonaktifkan. Karenanya batang Q A terhubung ke input clock FF-B dan batang Q B terhubung ke input clock FF-C. Koneksi ini akan menghasilkan penghitung turun. Jadi dengan M = 1 rangkaian bekerja sebagai penghitung turun.

Penghitung Modulus (Penghitung MOD-N)

Penghitung riak 2-bit disebut sebagai penghitung MOD-4 dan pencacah riak 3-bit disebut sebagai penghitung MOD-8. Jadi secara umum, pencacah riak n-bit disebut pencacah modulo-N. Dimana, nomor MOD = 2 ⁿ .

Jenis modulus

• 2-bit naik atau turun (MOD-4)
• 3-bit naik atau turun (MOD-8)
• 4-bit naik atau turun (MOD-16)

Penerapan penghitung

• Penghitung frekuensi
• Jam digital
• Pengukuran waktu
• Konverter A ke D.
• Sirkuit pembagi frekuensi
• Generator gelombang segitiga digital.

Ingatan sama seperti otak manusia. Digunakan untuk menyimpan data dan instruksi. Memori komputer adalah ruang penyimpanan di komputer tempat data akan diproses dan instruksi yang diperlukan untuk pemrosesan disimpan.

Memori dibagi menjadi beberapa bagian kecil. Setiap bagian disebut sel. Setiap lokasi atau sel memiliki alamat unik yang bervariasi dari nol hingga ukuran memori minus satu.

Misalnya jika komputer memiliki 64k kata, maka unit memori ini memiliki lokasi memori 64 * 1024 = 65536. Alamat lokasi ini bervariasi dari 0 hingga 65535.

Memori terutama terdiri dari dua jenis

• Internal Memory - memori cache dan memori utama / utama

• External Memory - disk magnetik / disk optik dll.

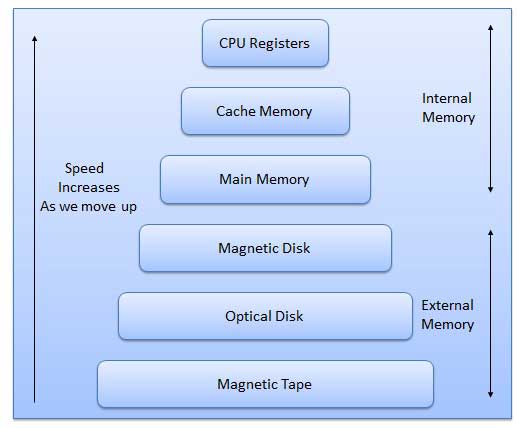
Karakteristik Hirarki Memori mengikuti ketika kita pergi dari atas ke bawah.

• Kapasitas dalam hal penyimpanan meningkat.
• Biaya per bit penyimpanan menurun.
• Frekuensi akses memori oleh CPU menurun.
• Waktu akses oleh CPU meningkat.

RAM

RAM merupakan memori internal CPU untuk menyimpan data, program dan hasil program. Ini adalah memori baca / tulis. Ini disebut memori akses acak (RAM).

Karena waktu akses dalam RAM tidak bergantung pada alamat kata, setiap lokasi penyimpanan di dalam memori mudah dijangkau seperti lokasi lain & membutuhkan waktu yang sama. Kami dapat menjangkau memori secara acak & sangat cepat tetapi juga bisa sangat mahal.

RAM bersifat volatile, yaitu data yang tersimpan di dalamnya hilang saat komputer kita matikan atau jika ada listrik mati. Oleh karena itu, cadangan sistem daya tak terputus (UPS) sering digunakan dengan komputer. RAM itu kecil, baik dari segi ukuran fisiknya maupun dalam jumlah data yang dapat disimpannya.

RAM terdiri dari dua jenis

• RAM Statis (SRAM)
• RAM Dinamis (DRAM)

RAM Statis (SRAM)

Kata staticmenunjukkan bahwa memori mempertahankan isinya selama daya tetap diterapkan. Namun, data akan hilang ketika listrik turun karena sifatnya yang mudah berubah. Chip SRAM menggunakan matriks 6-transistor dan tanpa kapasitor. Transistor tidak memerlukan daya untuk mencegah kebocoran, jadi SRAM tidak perlu disegarkan secara teratur.

Karena ruang ekstra dalam matriks, SRAM menggunakan lebih banyak chip daripada DRAM untuk jumlah ruang penyimpanan yang sama, sehingga membuat biaya produksi lebih tinggi.

RAM statis digunakan karena memori cache harus sangat cepat dan kecil.

RAM Dinamis (DRAM)

DRAM, tidak seperti SRAM, harus terus menerus refreshedagar dapat menjaga data. Ini dilakukan dengan menempatkan memori pada sirkuit penyegaran yang menulis ulang data beberapa ratus kali per detik. DRAM digunakan untuk sebagian besar memori sistem karena murah dan kecil. Semua DRAM terdiri dari sel memori. Sel-sel ini terdiri dari satu kapasitor dan satu transistor.

ROM

ROM adalah singkatan dari Read Only Memory. Memori yang darinya kita hanya bisa membaca tapi tidak bisa menulis padanya. Jenis memori ini tidak mudah menguap. Informasi tersebut disimpan secara permanen dalam memori tersebut selama pembuatan.

ROM, menyimpan instruksi seperti yang diperlukan untuk menyalakan komputer saat listrik pertama kali dihidupkan, operasi ini disebut sebagai bootstrap. Chip ROM tidak hanya digunakan di komputer tetapi juga di barang elektronik lainnya seperti mesin cuci dan oven microwave.

Berikut adalah berbagai jenis ROM -

MROM (ROM bertopeng)

ROM pertama adalah perangkat terprogram yang berisi kumpulan data atau instruksi yang telah diprogram sebelumnya. ROM semacam ini dikenal sebagai ROM bertopeng. Ini adalah ROM yang tidak mahal.

PROM (Memori Hanya Baca yang Dapat Diprogram)

PROM adalah memori hanya-baca yang dapat dimodifikasi hanya sekali oleh pengguna. Pengguna membeli PROM kosong dan memasukkan konten yang diinginkan menggunakan programmer PROM. Di dalam chip PROM ada sekring kecil yang terbakar selama pemrograman. Itu hanya bisa diprogram sekali dan tidak bisa dihapus.

EPROM (Memori Hanya Baca yang Dapat Dihapus dan Dapat Diprogram)

EPROM dapat dihapus dengan memaparkannya ke sinar ultra-violet selama hingga 40 menit. Biasanya, penghapus EPROM mencapai fungsi ini. Selama pemrograman, muatan listrik terjebak di daerah gerbang yang terisolasi. Pungutan tersebut ditahan selama lebih dari sepuluh tahun karena muatan tersebut tidak memiliki jalur kebocoran. Untuk menghapus muatan ini, sinar ultra violet dilewatkan melalui jendela kristal kuarsa (tutup). Paparan sinar ultra-violet ini menghilangkan muatannya. Selama penggunaan normal, tutup kuarsa ditutup dengan stiker.

EEPROM (Memori Hanya Baca yang Dapat Dihapus Secara Elektrik dan Dapat Diprogram)

EEPROM diprogram dan dihapus secara elektrik. Itu dapat dihapus dan diprogram ulang sekitar sepuluh ribu kali. Baik penghapusan maupun pemrograman membutuhkan waktu sekitar 4 hingga 10 ms (milidetik). Di EEPROM, lokasi mana pun dapat dihapus dan diprogram secara selektif. EEPROM dapat dihapus satu byte pada satu waktu, daripada menghapus seluruh chip. Oleh karena itu, proses pemrograman ulang bersifat fleksibel tetapi lambat.

Memori Akses Serial

Akses sekuensial berarti sistem harus mencari perangkat penyimpanan dari awal alamat memori hingga menemukan bagian data yang diperlukan. Perangkat memori yang mendukung akses tersebut dinamakan Sequential Access Memory atau Serial Access Memory. Pita magnetik adalah contoh memori akses serial.

Memori Akses Langsung

Memori akses langsung atau Random Access Memory, mengacu pada kondisi di mana sistem dapat langsung menuju informasi yang diinginkan pengguna. Perangkat memori yang mendukung akses tersebut disebut Memori Akses Langsung. Disk magnetik, disk optik adalah contoh memori akses langsung.

Memori Cache

Memori cache adalah memori semikonduktor berkecepatan sangat tinggi yang dapat mempercepat CPU. Ini bertindak sebagai penyangga antara CPU dan memori utama. Ini digunakan untuk menampung bagian-bagian data dan program yang paling sering digunakan oleh CPU. Bagian-bagian data dan program, ditransfer dari disk ke memori cache oleh sistem operasi, dari mana CPU dapat mengaksesnya.

Keuntungan

• Memori cache lebih cepat dari memori utama.
• Ini mengkonsumsi lebih sedikit waktu akses dibandingkan dengan memori utama.
• Ini menyimpan program yang dapat dijalankan dalam waktu singkat.
• Ini menyimpan data untuk penggunaan sementara.

Kekurangan

• Memori cache memiliki kapasitas terbatas.
• Itu sangat mahal.

Memori virtual adalah teknik yang memungkinkan eksekusi proses yang tidak sepenuhnya tersedia di memori. Keuntungan utama yang terlihat dari skema ini adalah bahwa program dapat lebih besar dari memori fisik. Memori virtual adalah pemisahan memori logis pengguna dari memori fisik.

Pemisahan ini memungkinkan memori virtual yang sangat besar disediakan untuk pemrogram jika hanya tersedia memori fisik yang lebih kecil. Berikut adalah situasinya, ketika seluruh program tidak perlu dimuat sepenuhnya di memori utama.

• Rutinitas penanganan kesalahan tertulis pengguna hanya digunakan ketika terjadi kesalahan dalam data atau komputasi.

• Opsi dan fitur tertentu dari suatu program mungkin jarang digunakan.

• Banyak tabel diberi jumlah ruang alamat tetap meskipun hanya sejumlah kecil tabel yang benar-benar digunakan.

• Kemampuan untuk mengeksekusi program yang hanya sebagian di memori akan memberikan banyak keuntungan.

• Lebih sedikit jumlah I / O yang dibutuhkan untuk memuat atau menukar setiap program pengguna ke dalam memori.

• Program tidak lagi dibatasi oleh jumlah memori fisik yang tersedia.

• Setiap program pengguna dapat menggunakan lebih sedikit memori fisik, lebih banyak program dapat dijalankan pada waktu yang sama, dengan peningkatan yang sesuai dalam pemanfaatan dan throughput CPU.

Memori Bantu

Memori tambahan jauh lebih besar ukurannya daripada memori utama tetapi lebih lambat. Biasanya menyimpan program sistem, instruksi dan file data. Ini juga dikenal sebagai memori sekunder. Ini juga dapat digunakan sebagai memori tambahan / virtual jika kapasitas memori utama telah terlampaui. Memori sekunder tidak dapat diakses secara langsung oleh prosesor. Pertama data / informasi dari auxiliary memory dipindahkan ke memori utama dan selanjutnya informasi tersebut dapat diakses oleh CPU. Karakteristik Auxiliary Memory adalah sebagai berikut -

• Non-volatile memory - Data tidak hilang saat listrik dimatikan.

• Reusable - Data tetap berada di penyimpanan sekunder secara permanen sampai tidak ditimpa atau dihapus oleh pengguna.

• Reliable - Data dalam penyimpanan sekunder aman karena stabilitas fisik yang tinggi dari perangkat penyimpanan sekunder.

• Convenience - Dengan bantuan perangkat lunak komputer, orang yang berwenang dapat mencari dan mengakses data dengan cepat.

• Capacity - Penyimpanan sekunder dapat menyimpan data dalam jumlah besar dalam kumpulan beberapa disk.

• Cost - Jauh lebih murah untuk menyimpan data pada tape atau disk daripada memori primer.

Unit pemrosesan mikro identik dengan unit pemrosesan pusat, CPU yang digunakan di komputer tradisional. Mikroprosesor (MPU) bertindak sebagai perangkat atau sekelompok perangkat yang melakukan tugas berikut.

• berkomunikasi dengan perangkat periferal
• berikan sinyal waktu
• aliran data langsung
• melakukan tugas komputer seperti yang ditentukan oleh instruksi di memori

8085 Mikroprosesor

Mikroprosesor 8085 adalah mikroprosesor serba guna 8-bit yang mampu menangani memori 64k. Prosesor ini memiliki empat puluh pin, membutuhkan catu daya tunggal +5 V dan clock fase tunggal 3 MHz.

Diagram Blok

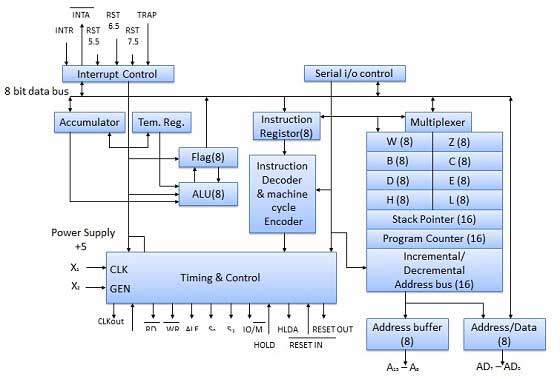
ALU

ALU melakukan fungsi komputasi mikroprosesor. Ini termasuk akumulator, register sementara, rangkaian aritmatika & logika & dan lima bendera. Hasil disimpan di akumulator & bendera.

Diagram Blok

Aki

Ini adalah register 8-bit yang merupakan bagian dari ALU. Register ini digunakan untuk menyimpan data 8-bit & dalam melakukan operasi aritmatika & logika. Hasil operasi disimpan dalam akumulator.

Diagram

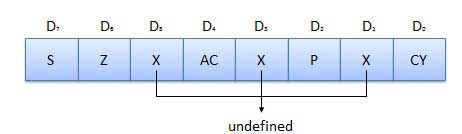
Bendera

Bendera dapat diprogram. Mereka dapat digunakan untuk menyimpan dan mentransfer data dari register dengan menggunakan instruksi. ALU mencakup lima flip-flop yang disetel dan disetel ulang sesuai dengan kondisi data di akumulator dan register lainnya.

• S (Sign) flag- Setelah eksekusi operasi aritmatika, jika bit D ₇ hasilnya adalah 1, tanda flag diset. Ini digunakan untuk nomor yang ditandatangani. Dalam satu byte, jika D ₇ adalah 1 berarti angka negatif. Jika nol berarti bilangan positif.

• Z (Zero) flag - Bendera nol disetel jika hasil operasi ALU adalah 0.

• AC (Auxiliary Carry) flag- Dalam operasi aritmatika, saat carry dihasilkan oleh digit D3 dan diteruskan ke digit D ₄ , bendera AC disetel. Bendera ini hanya digunakan untuk operasi BCD internal.

• P (Parity) flag- Setelah operasi aritmatika atau logika, jika hasil memiliki bilangan genap 1, bendera ditetapkan. Jika memiliki angka ganjil 1s, flag direset.

• C (Carry) flag - Jika hasil operasi aritmatika adalah carry, flag carry akan disetel, jika tidak maka reset.

Bagian daftar

Ini pada dasarnya adalah perangkat penyimpanan dan mentransfer data dari register dengan menggunakan instruksi.

• Stack Pointer (SP)- Penunjuk tumpukan juga merupakan register 16-bit yang digunakan sebagai penunjuk memori. Ini menunjuk ke lokasi memori di memori Baca / Tulis yang dikenal sebagai tumpukan. Di sela-sela pelaksanaan program, terkadang data disimpan di stack. Awal tumpukan ditentukan dengan memuat alamat 16-bit di penunjuk tumpukan.

• Program Counter (PC)- Register 16-bit ini berhubungan dengan operasi keempat untuk mengurutkan eksekusi instruksi. Register ini juga merupakan penunjuk memori. Lokasi memori memiliki alamat 16-bit. Ini digunakan untuk menyimpan alamat eksekusi. Fungsi pencacah program adalah untuk menunjuk ke alamat memori dari mana byte berikutnya akan diambil.

• Storage registers- Register ini menyimpan data 8-bit selama eksekusi program. Register ini diidentifikasi sebagai B, C, D, E, H, L. Mereka dapat digabungkan sebagai pasangan register BC, DE dan HL untuk melakukan beberapa operasi 16 bit.

Bagian Waktu dan Kontrol

Unit ini bertanggung jawab untuk menyinkronkan operasi Mikroprosesor sesuai dengan pulsa clock dan untuk menghasilkan sinyal kontrol yang diperlukan untuk kelancaran komunikasi antara Mikroprosesor dan perangkat periferal. Sinyal bar RD dan WR bar adalah pulsa sinkron yang menunjukkan apakah data tersedia pada bus data atau tidak. Unit kontrol bertanggung jawab untuk mengontrol aliran data antara mikroprosesor, memori, dan perangkat periferal.

Diagram PIN

Semua sinyal dapat diklasifikasikan menjadi enam kelompok

SN	Kelompok	Deskripsi
1	Address bus	Mikroprosesor 8085 memiliki 8 jalur sinyal, A 15 - A 8 yang searah dan digunakan sebagai bus alamat tingkat tinggi.
2	Data bus	Garis sinyal AD7 - AD0 adalah dua arah untuk tujuan ganda. Mereka digunakan sebagai bus alamat tingkat rendah serta bus data.
3	Control signal and Status signal	Sinyal Kontrol RD bar- Ini adalah sinyal kontrol baca (aktif rendah). Jika aktif maka memori membaca datanya. WR bar- Ini adalah sinyal kontrol tulis (aktif rendah). Ini aktif ketika ditulis ke dalam memori yang dipilih. Sinyal status ALU (Address Latch Enable)- Saat ALU tinggi. 8085 mikroprosesor menggunakan bus alamat. Saat ALU rendah. Mikroprosesor 8085 menggunakan bus data. IO/M bar- Ini adalah sinyal status yang digunakan untuk membedakan antara operasi i / o dan memori. Ketika tinggi, ini menunjukkan operasi i / o dan ketika rendah, ini menunjukkan operasi memori. S1 and S0 - Sinyal status ini, mirip dengan i / o dan bilah memori, dapat mengidentifikasi berbagai operasi, tetapi jarang digunakan dalam sistem kecil.
4	Power supply and frequency signal	Vcc - Catu daya + 5v. Vss - referensi dasar. X, X- Kristal dihubungkan pada dua pin ini. Frekuensi internal dibagi oleh dua sistem operasi pada 3-MHz, kristal harus memiliki frekuensi 6-MHz. CLK out - Sinyal ini dapat digunakan sebagai jam sistem untuk perangkat lain.
5	Externally initiated signal	INTR (i/p) - Ganggu permintaan. INTA bar (o/p) - Ini digunakan sebagai pengakuan interupsi. TRAP (i/p) - Ini adalah interupsi non-maskable dan memiliki prioritas tertinggi. HOLD (i/p) - Digunakan untuk mengadakan program pelaksana. HLDA (o/p) - Tahan akui. READY (i/p) - Sinyal ini digunakan untuk menunda siklus baca atau tulis mikroprosesor hingga periferal yang merespons lambat siap menerima atau mengirim data. RESET IN bar - Ketika sinyal pada pin ini melemah, penghitung program disetel ke nol, bus dinyatakan tiga, & MPU disetel ulang. RESET OUT- Sinyal ini menunjukkan bahwa MPU sedang disetel ulang. Sinyal tersebut dapat digunakan untuk mengatur ulang perangkat lain. RST 7.5, RST 6.5, RST 5.5 (Request interrupt)- Ini digunakan untuk mentransfer kontrol program ke lokasi memori tertentu. Mereka memiliki prioritas lebih tinggi daripada interupsi INTR.
6	Serial I/O ports	Mikroprosesor 8085 memiliki dua sinyal untuk mengimplementasikan transmisi serial data input serial dan data output serial.

Format Instruksi

Setiap instruksi diwakili oleh urutan bit di dalam komputer. Instruksi dibagi menjadi kelompok bit yang disebut field. Cara instruksi diekspresikan dikenal sebagai format instruksi. Biasanya direpresentasikan dalam bentuk kotak persegi panjang. Format instruksi mungkin dari jenis berikut.

Format Instruksi Variabel

Ini adalah format instruksi di mana panjang instruksi bervariasi berdasarkan opcode & penentu alamat. Sebagai Contoh, instruksi VAX bervariasi antara 1 dan 53 byte sementara instruksi X86 bervariasi antara 1 dan 17 byte.

Format

Keuntungan

Format ini memiliki kepadatan kode yang baik.

Kekurangan

Format instruksi ini sangat sulit untuk didekode dan disalurkan.

Format Instruksi Tetap

Dalam format instruksi jenis ini, semua instruksi memiliki ukuran yang sama. Misalnya, MIPS, Power PC, Alpha, ARM.

Format

Keuntungan

Mereka mudah didekode & disalurkan.

Kekurangan

Mereka tidak memiliki kepadatan kode yang baik.

Format Instruksi Hibrid

Dalam jenis format instruksi ini, kami memiliki beberapa panjang format yang ditentukan oleh opcode. Misalnya, IBM 360/70, MIPS 16, Thumb.

Format

Keuntungan

Kompromi antara kepadatan kode & instruksi jenis ini sangat mudah untuk diuraikan.

Mengatasi Mode

Mode pengalamatan menyediakan berbagai cara untuk mengakses alamat ke data yang diberikan ke prosesor. Data yang dioperasikan disimpan di lokasi memori, setiap instruksi membutuhkan data tertentu yang harus dioperasikan. Ada berbagai teknik untuk menentukan alamat data. Teknik ini disebut Mode Pengalamatan.

• Direct addressing mode- Dalam mode pengalamatan langsung, alamat operan diberikan dalam instruksi dan data tersedia di lokasi memori yang disediakan dalam instruksi. Kami akan memindahkan data ini di lokasi yang diinginkan.

• Indirect addressing mode- Dalam mode pengalamatan tidak langsung, instruksi menentukan register yang berisi alamat operan. Baik RAM internal maupun RAM eksternal dapat diakses melalui mode pengalamatan tidak langsung.

• Immediate addressing mode- Dalam mode pengalamatan langsung, data langsung diberikan di operan yang memindahkan data di akumulator. Ini sangat cepat.

• Relative addressing mode- Dalam mode alamat relatif, alamat efektif ditentukan oleh mode indeks dengan menggunakan penghitung program sebagai pengganti register prosesor tujuan umum. Mode ini disebut mode alamat relatif.

• Index addressing mode- Dalam mode alamat indeks, alamat efektif dari operan dihasilkan dengan menambahkan nilai konten ke konten register. Mode ini disebut mode alamat indeks.