Konsep Konvolusi
Tutorial ini adalah tentang salah satu konsep sinyal dan sistem yang sangat penting. Kami sepenuhnya akan membahas konvolusi. Apa itu? Kenapa sih? Apa yang bisa kita capai dengan itu?
Kami akan mulai membahas konvolusi dari dasar-dasar pemrosesan gambar.
Apa itu pemrosesan gambar
Seperti yang telah kita bahas dalam pengantar tutorial pemrosesan gambar dan dalam sinyal dan sistem bahwa pemrosesan gambar kurang lebih merupakan studi tentang sinyal dan sistem karena gambar tidak lain adalah sinyal dua dimensi.
Juga telah kita bahas, bahwa dalam pengolahan citra, kita sedang mengembangkan sistem yang masukannya berupa citra dan keluarannya berupa citra. Ini secara bergambar direpresentasikan sebagai.
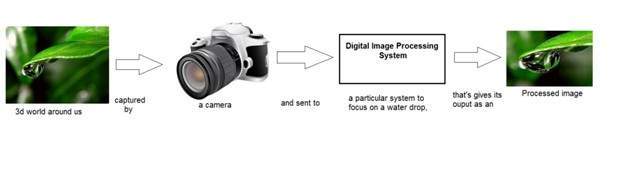
Kotak yang ditunjukkan pada gambar di atas berlabel "Sistem Pengolahan Citra Digital" dapat dianggap sebagai kotak hitam
Itu bisa lebih baik direpresentasikan sebagai:

Kemana kita sampai sekarang
Sampai saat ini kita telah membahas dua metode penting untuk memanipulasi gambar. Atau dengan kata lain kita dapat mengatakan bahwa kotak hitam kita bekerja dengan dua cara yang berbeda sampai saat ini.
Dua cara berbeda untuk memanipulasi gambar adalah
Grafik (Histogram)

Metode ini dikenal dengan pemrosesan histogram. Kami telah membahasnya secara rinci di tutorial sebelumnya untuk meningkatkan kontras, peningkatan gambar, kecerahan, dll
Fungsi transformasi
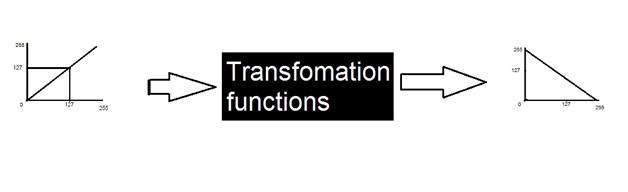
Metode ini dikenal sebagai transformasi, di mana kita membahas berbagai jenis transformasi dan beberapa transformasi tingkat abu-abu
Cara lain untuk menangani gambar
Di sini kita akan membahas metode lain untuk menangani gambar. Metode lain ini dikenal sebagai konvolusi. Biasanya black box (sistem) yang digunakan untuk pengolahan citra adalah sistem LTI atau sistem invarian waktu linier. Yang kami maksud dengan linier adalah sistem yang keluarannya selalu linier, baik log maupun eksponen atau lainnya. Dan dengan time invariant yang kami maksud adalah sebuah sistem yang tetap sama selama waktu.
Jadi sekarang kita akan menggunakan metode ketiga ini. Itu dapat direpresentasikan sebagai.

Ini dapat direpresentasikan secara matematis sebagai dua cara
g(x,y) = h(x,y) * f(x,y)
Ini dapat dijelaskan sebagai "topeng yang berbelit-belit dengan gambar".
Atau
g(x,y) = f(x,y) * h(x,y)
Ini dapat dijelaskan sebagai "gambar yang dibelit topeng".
Ada dua cara untuk merepresentasikan ini karena operator konvolusi (*) bersifat komutatif. H (x, y) adalah mask atau filter.
Apa itu topeng?
Masker juga merupakan sinyal. Itu dapat diwakili oleh matriks dua dimensi. Topeng biasanya dari urutan 1x1, 3x3, 5x5, 7x7. Sebuah topeng harus selalu berjumlah ganjil, karena jika tidak, Anda tidak dapat menemukan bagian tengah topeng. Mengapa kita perlu menemukan bagian tengah topeng. Jawabannya ada di bawah ini, dalam topik, bagaimana melakukan konvolusi?
Bagaimana cara melakukan konvolusi?
Untuk melakukan konvolusi pada gambar, langkah-langkah berikut harus diambil.
- Balikkan topeng (secara horizontal dan vertikal) hanya sekali
- Geser topeng ke atas gambar.
- Kalikan elemen yang sesuai lalu tambahkan
- Ulangi prosedur ini sampai semua nilai gambar telah dihitung.
Contoh konvolusi
Mari kita lakukan konvolusi. Langkah 1 adalah membalik topeng.
Topeng
Mari kita ambil topeng kita menjadi ini.
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
Balik topeng secara horizontal
| 3 | 2 | 1 |
| 6 | 5 | 4 |
| 9 | 8 | 7 |
Balik topeng secara vertikal
| 9 | 8 | 7 |
| 6 | 5 | 4 |
| 3 | 2 | 1 |
Gambar
Mari kita pertimbangkan sebuah gambar menjadi seperti ini
| 2 | 4 | 6 |
| 8 | 10 | 12 |
| 14 | 16 | 18 |
Lilitan
Konvolusi topeng di atas gambar. Itu dilakukan dengan cara ini. Tempatkan bagian tengah topeng di setiap elemen gambar. Kalikan elemen yang sesuai lalu tambahkan, dan tempelkan hasilnya ke elemen gambar tempat Anda menempatkan pusat mask.
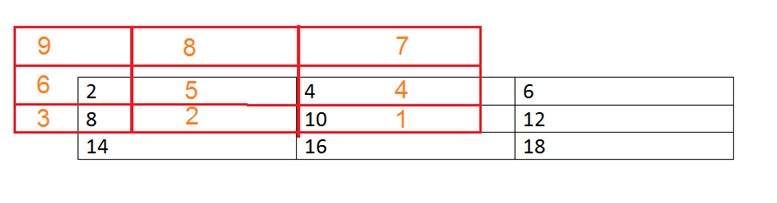
Kotak dengan warna merah adalah topeng, dan nilai oranye adalah nilai topeng. Kotak dan nilai warna hitam adalah milik gambar. Sekarang untuk piksel pertama gambar, nilainya akan dihitung sebagai
Pixel pertama = (5 * 2) + (4 * 4) + (2 * 8) + (1 * 10)
= 10 + 16 + 16 + 10
= 52
Tempatkan 52 pada gambar asli pada indeks pertama dan ulangi prosedur ini untuk setiap piksel gambar.
Mengapa Konvolusi
Konvolusi dapat mencapai sesuatu, yang tidak dapat dicapai oleh dua metode manipulasi gambar sebelumnya. Itu termasuk pengaburan, penajaman, deteksi tepi, pengurangan kebisingan dll