Teori Grafik - Penutup

Grafik penutup adalah subgraf yang berisi semua simpul atau semua sisi yang berhubungan dengan graf lainnya. Sebuah subgrafik yang berisi semua simpul disebut aline/edge covering. Sebuah subgrafik yang berisi semua tepi disebut avertex covering.

Penutup Garis

Misalkan G = (V, E) adalah grafik. Himpunan bagian C (E) disebut garis yang menutupi G jika setiap simpul dari G bersisian dengan setidaknya satu sisi di C, yaitu,

derajat (V) ≥ 1 ∀ V ∈ G

karena setiap simpul terhubung dengan simpul lain oleh sebuah sisi. Karenanya ia memiliki derajat minimal 1.

Example

Perhatikan grafik berikut -

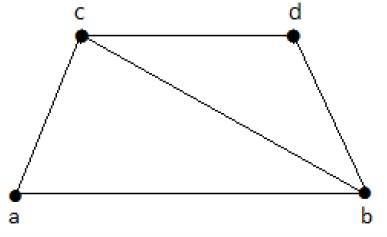
Subgrafinya yang memiliki penutup garis adalah sebagai berikut -

C ₁ = {{a, b}, {c, d}}

C ₂ = {{a, d}, {b, c}}

C ₃ = {{a, b}, {b, c}, {b, d}}

C ₄ = {{a, b}, {b, c}, {c, d}}

Penutupan garis 'G' tidak ada jika dan hanya jika 'G' memiliki simpul terisolasi. Penutupan garis dari grafik dengan simpul 'n' memiliki setidaknya [n / 2] sisi.

Minimal Line Covering

Sebuah garis yang menutupi C dari grafik G dikatakan minimal if no edge can be deleted from C.

Example

Pada grafik di atas, subgraf yang memiliki penutup garis adalah sebagai berikut:

C ₁ = {{a, b}, {c, d}}

C ₂ = {{a, d}, {b, c}}

C ₃ = {{a, b}, {b, c}, {b, d}}

C ₄ = {{a, b}, {b, c}, {c, d}}

Di sini C ₁ , C ₂ , C ₃ adalah penutup garis minimal, sedangkan C ₄ bukan karena kita bisa menghapus {b, c}.

Penutupan Garis Minimum

Itu juga dikenal sebagai Smallest Minimal Line Covering. Penutupan garis minimal dengan jumlah tepi minimum disebut penutup garis minimum 'G'. Jumlah tepi dalam garis minimum yang menutupi di 'G' disebutline covering numberdari 'G' (α ₁ ).

Example

Dalam contoh di atas, C ₁ dan C ₂ adalah garis penutup minimum dari G dan α ₁ = 2.

Setiap penutup garis mengandung penutup garis minimal.
Setiap penutup garis tidak mengandung penutup garis minimum (C ₃ tidak mengandung penutup garis minimum.
Tidak ada penutup garis minimal yang mengandung siklus.
Jika suatu garis yang menutupi 'C' tidak memiliki jalur dengan panjang 3 atau lebih, maka 'C' adalah garis penutup minimal karena semua komponen 'C' adalah grafik bintang dan dari grafik bintang, tidak ada tepi yang dapat dihapus.

Vertex Covering

Misalkan 'G' = (V, E) menjadi grafik. Himpunan bagian K dari V disebut puncak yang menutupi 'G', jika setiap tepi 'G' bersisian dengan atau ditutupi oleh simpul di 'K'.

Example

Perhatikan grafik berikut -

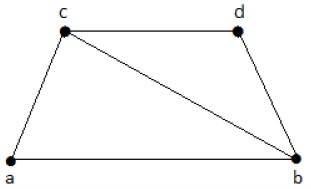
Subgrafik yang dapat diturunkan dari grafik di atas adalah sebagai berikut -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

K ₄ = {a, d}

Di sini, K ₁ , K ₂ , dan K ₃ memiliki simpul yang menutupi, sedangkan K ₄ tidak memiliki simpul yang menutupi karena tidak menutupi tepi {bc}.

Minimal Vertex Covering

Sebuah simpul 'K' dari graf 'G' dikatakan sebagai simpul minimal yang menutupi jika tidak ada simpul yang dapat dihapus dari 'K'.

Example

Pada grafik di atas, subgrafik yang memiliki penutup puncak adalah sebagai berikut -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

Di sini, K ₁ dan K ₂ adalah penutup simpul minimal, sedangkan di K ₃ , simpul 'd' bisa dihapus.

Penutupan Vertex Minimum

Ia juga dikenal sebagai penutup simpul minimal terkecil. Sebuah simpul minimal yang menutupi graf 'G' dengan jumlah simpul minimal disebut penutup simpul minimum.

Jumlah simpul pada simpul minimal yang menutupi 'G' disebut simpul yang menutupi bilangan G (α ₂ ).

Example

Pada grafik berikut, subgrafik yang memiliki penutup puncak adalah sebagai berikut -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}