Teori Grafik - Set Independen

Set independen diwakili dalam set, di mana

• seharusnya tidak ada any edges adjacent to each other. Seharusnya tidak ada simpul yang sama antara dua sisi.

• seharusnya tidak ada any vertices adjacent to each other. Seharusnya tidak ada tepi yang sama antara dua simpul mana pun.

Set Jalur Independen

Misalkan 'G' = (V, E) menjadi grafik. Himpunan bagian L dari E disebut himpunan garis independen 'G' jika tidak ada dua sisi di L yang berdekatan. Himpunan seperti itu disebut himpunan garis independen.

Example

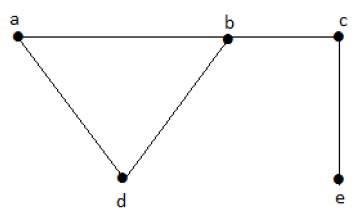
Mari kita pertimbangkan subset berikut -

L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}

Dalam contoh ini, himpunan bagian L2 dan L3 jelas bukan tepian yang berdekatan dalam grafik yang diberikan. Mereka adalah kumpulan garis independen. Namun L1 bukanlah himpunan garis independen, karena untuk membuat himpunan garis independen, harus ada setidaknya dua tepi.

Set Garis Independen Maksimal

Himpunan garis independen dikatakan himpunan garis independen maksimal dari grafik 'G' jika tidak ada tepi lain dari 'G' yang dapat ditambahkan ke 'L'.

Example

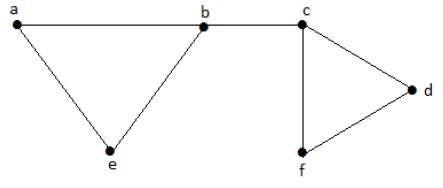
Mari kita pertimbangkan subset berikut -

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L ₂ dan L ₃ adalah kumpulan baris independen maksimal / pencocokan maksimal. Adapun hanya untuk dua himpunan bagian ini, tidak ada kemungkinan untuk menambahkan tepi lain yang tidak berdekatan. Oleh karena itu, kedua himpunan bagian ini dianggap sebagai himpunan garis independen maksimal.

Set Garis Independen Maksimum

Himpunan garis independen maksimum 'G' dengan jumlah tepi maksimum disebut himpunan garis independen maksimum 'G'.

Number of edges in a maximum independent line set of G (β1)
   = Line independent number of G
   = Matching number of G

Example

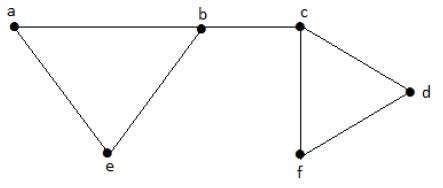
Mari kita pertimbangkan subset berikut -

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L ₃ adalah himpunan garis bebas maksimum G dengan tepi maksimum yang bukan merupakan tepi yang berdekatan dalam grafik dan dilambangkan dengan β1 = 3.

Note - Untuk semua graf G tanpa simpul terisolasi,

α1 + β1 = jumlah simpul dalam sebuah grafik = | V |

Example

Nomor penutup garis K _n / C _n / w _n ,

$$ \ alpha 1 = \ lceil \ frac {n} {2} \ rceil \ begin {cases} \ frac {n} {2} \: if \: n \: is \: even \\\ frac {n + 1} {2} \: jika \: n \: adalah \: ganjil \ end {kasus} $$

Bilangan bebas garis (Nomor yang cocok) = β ₁ = [n / 2] α ₁ + β ₁ = n.

Set Vertex Independen

Misalkan 'G' = (V, E) menjadi grafik. Himpunan bagian dari 'V' disebut himpunan independen dari 'G' jika tidak ada dua simpul di 'S' yang berdekatan.

Example

Pertimbangkan subset berikut dari grafik di atas -

S1 = {e}

S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Jelas S ₁ bukan himpunan simpul independen, karena untuk mendapatkan himpunan simpul independen, setidaknya harus ada dua simpul dalam dari sebuah graf. Tapi di sini bukan itu masalahnya. Himpunan bagian S ₂ , S ₃ , dan S ₄ adalah himpunan simpul independen karena tidak ada simpul yang berdekatan dengan satu simpul manapun dari himpunan bagian tersebut.

Set Vertex Independen Maksimal

Misalkan 'G' adalah sebuah graf, maka himpunan simpul independen dari 'G' dikatakan maksimal jika tidak ada simpul lain dari 'G' yang dapat ditambahkan ke 'S'.

Example

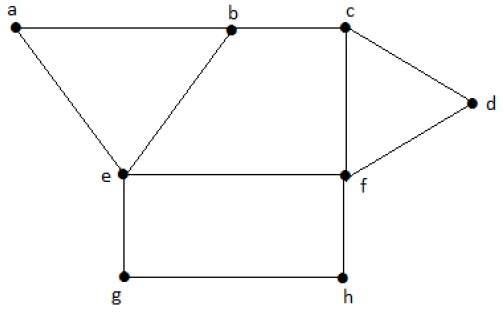
Perhatikan subset berikut dari grafik di atas.

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

S ₂ dan S ₃ adalah himpunan puncak independen maksimal dari 'G'. Di S ₁ dan S ₄ , kita bisa menambahkan simpul lain; tetapi di S ₂ dan S ₃ , kita tidak bisa menambahkan simpul lain.

Set Vertex Independen Maksimum

Himpunan simpul independen maksimal 'G' dengan jumlah simpul maksimal disebut sebagai himpunan simpul bebas maksimum.

Example

Pertimbangkan subset berikut dari grafik di atas -

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Hanya S ₃ adalah himpunan simpul independen maksimum, karena mencakup jumlah simpul tertinggi. Jumlah simpul dalam himpunan simpul bebas maksimum 'G' disebut bilangan simpul bebas G (β ₂ ).

Example

Untuk grafik lengkap K _n ,

Simpul yang menutupi nomor = α ₂ = n − 1

Bilangan bebas simpul = β ₂ = 1

Anda memiliki α ₂ + β ₂ = n

Dalam graf lengkap, setiap simpul berdekatan dengan simpul yang tersisa (n - 1). Oleh karena itu, himpunan independen maksimum K _n hanya berisi satu simpul.

Oleh karena itu, β ₂ = 1

dan α ₂ = | v | - β ₂ = n-1

Note - Untuk semua grafik 'G' = (V, E)

• α ₂ + β ₂ = | v |
• Jika 'S' adalah himpunan puncak independen dari 'G', maka (V - S) adalah penutup puncak dari G.