Teori Grafik - Contoh
Dalam bab ini, kita akan membahas beberapa contoh standar untuk mendemonstrasikan konsep yang telah kita bahas di bab sebelumnya.
Contoh 1
Find the number of spanning trees in the following graph.
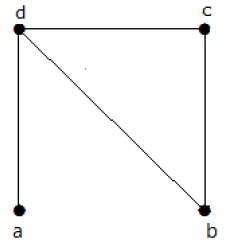
Larutan
Jumlah pohon merentang yang diperoleh dari grafik di atas adalah 3. Mereka adalah sebagai berikut -
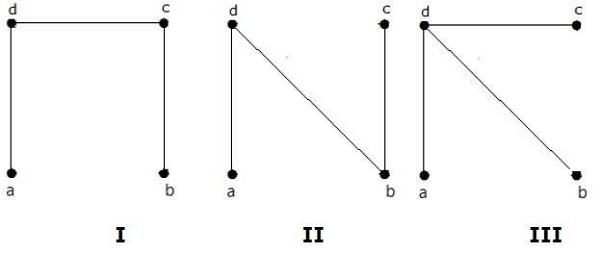
Ketiganya adalah pohon rentang untuk grafik yang diberikan. Di sini grafik I dan II isomorfik satu sama lain. Jelasnya, jumlah pohon rentang non-isomorfik adalah dua.
Contoh 2
How many simple non-isomorphic graphs are possible with 3 vertices?
Larutan
Ada 4 grafik non-isomorfik yang dimungkinkan dengan 3 simpul. Mereka ditunjukkan di bawah ini.
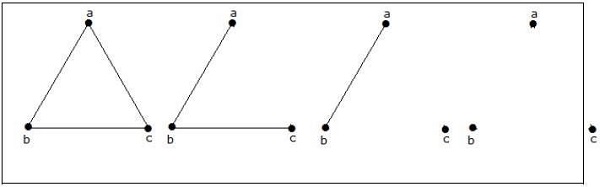
Contoh 3
Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.
Larutan
Dengan jumlah teorema derajat,
20 Σ i = 1 derajat (Vi) = 2 | E |
20 (3) = 2 | E |
| E | = 30
Dengan rumus Euler,
| V | + | R | = | E | + 2
20+ | R | = 30 + 2
| R | = 12
Sehingga jumlah wilayahnya ada 12.
Contoh 4
What is the chromatic number of complete graph Kn?
Larutan
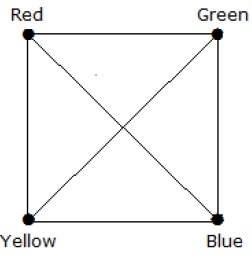
Dalam graf lengkap, setiap simpul bersebelahan adalah sisa (n – 1) simpul. Karenanya, setiap simpul membutuhkan warna baru. Karenanya bilangan kromatik K n = n.
Contoh 5
What is the matching number for the following graph?
Larutan
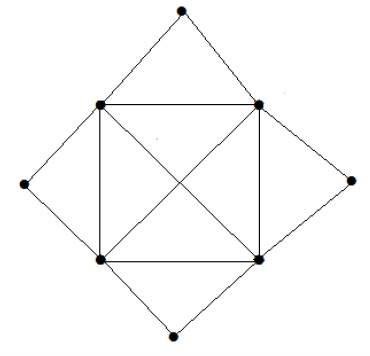
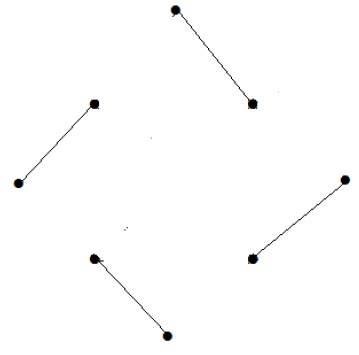
Jumlah simpul = 9
Kita hanya bisa mencocokkan 8 simpul.
Nomor yang cocok adalah 4.
Contoh 6
What is the line covering number of for the following graph?
Larutan
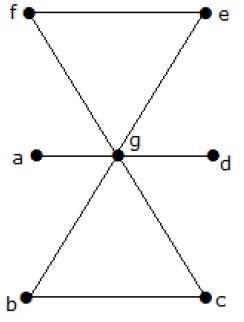
Jumlah simpul = | V | = n = 7
Nomor penutup garis = (α 1 ) ≥ [n / 2] = 3
α 1 ≥ 3
Dengan menggunakan 3 sisi, kita bisa menutupi semua simpul.
Oleh karena itu, nomor penutup garis adalah 3.