Teori Grafik - Panduan Cepat
Dalam ranah matematika dan ilmu komputer, teori graf adalah ilmu yang mempelajari graf yang berkenaan dengan hubungan antara tepi dan simpul . Ini adalah mata pelajaran yang populer memiliki aplikasinya dalam ilmu komputer, teknologi informasi, biosains, matematika, dan linguistik untuk beberapa nama. Tanpa basa-basi lagi, mari kita mulai dengan mendefinisikan grafik.
Apa itu Grafik?
Grafik adalah representasi bergambar dari sekumpulan objek di mana beberapa pasang objek dihubungkan oleh tautan. Objek yang saling berhubungan diwakili oleh poin yang disebut sebagaivertices, dan tautan yang menghubungkan simpul disebut edges.
Secara formal, grafik adalah sepasang himpunan (V, E), dimana Vadalah himpunan simpul dan E adalah himpunan tepi, menghubungkan pasangan simpul. Perhatikan grafik berikut -
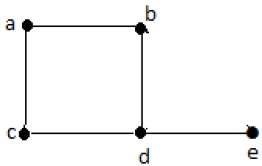
Pada grafik di atas,
V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de}
Aplikasi Teori Grafik
Teori graf memiliki aplikasinya dalam berbagai bidang teknik -
Electrical Engineering- Konsep teori grafik digunakan secara luas dalam merancang koneksi rangkaian. Jenis atau organisasi koneksi dinamai topologi. Beberapa contoh topologi adalah topologi star, bridge, series, dan parallel.
Computer Science- Teori grafik digunakan untuk mempelajari algoritma. Sebagai contoh,
- Algoritma Kruskal
- Algoritma Prim
- Algoritma Dijkstra
Computer Network - Hubungan antar komputer yang saling berhubungan dalam jaringan mengikuti prinsip teori grafik.
Science - Struktur molekul dan struktur kimia suatu zat, struktur DNA suatu organisme, dll., Diwakili oleh grafik.
Linguistics - Pohon parsing suatu bahasa dan tata bahasa menggunakan grafik.
General- Rute antar kota dapat direpresentasikan menggunakan grafik. Menggambarkan informasi terurut hierarkis seperti pohon keluarga dapat digunakan sebagai jenis grafik khusus yang disebut pohon.
Grafik adalah diagram titik dan garis yang terhubung ke titik. Ini memiliki setidaknya satu garis yang menghubungkan satu set dua simpul tanpa simpul yang menghubungkan dirinya sendiri. Konsep graf dalam teori graf berdiri pada beberapa istilah dasar seperti titik, garis, simpul, tepi, derajat simpul, sifat dari graf, dll. Di sini, pada bab ini, kita akan membahas dasar-dasar teori graf tersebut.
Titik
A pointadalah posisi tertentu dalam ruang satu dimensi, dua dimensi, atau tiga dimensi. Untuk pemahaman yang lebih baik, sebuah poin dapat dilambangkan dengan alfabet. Itu dapat diwakili dengan titik.
Contoh

Di sini, titik adalah titik bernama 'a'.
Garis
SEBUAH Lineadalah hubungan antara dua titik. Itu dapat diwakili dengan garis padat.
Example

Di sini, 'a' dan 'b' adalah poinnya. Hubungan antara dua titik ini disebut garis.
Puncak
Titik puncak adalah titik di mana banyak garis bertemu. Ini juga disebut anode. Mirip dengan titik, simpul juga dilambangkan dengan alfabet.
Example

Di sini, simpul diberi nama dengan alfabet 'a'.
Tepi
Sisi adalah istilah matematika untuk garis yang menghubungkan dua simpul. Banyak tepi dapat dibentuk dari satu simpul. Tanpa titik sudut, tepi tidak dapat dibentuk. Harus ada simpul awal dan simpul akhir untuk sebuah sisi.
Example

Di sini, 'a' dan 'b' adalah dua simpul dan hubungan di antara keduanya disebut tepi.
Grafik
Grafik 'G' didefinisikan sebagai G = (V, E) Dimana V adalah himpunan dari semua simpul dan E adalah himpunan dari semua sisi pada grafik.
Example 1

Dalam contoh di atas, ab, ac, cd, dan bd adalah tepi grafik. Demikian pula, a, b, c, dan d adalah simpul pada grafik.
Example 2
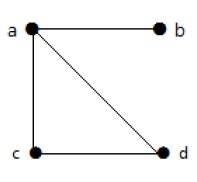
Pada graf ini terdapat empat buah simpul a, b, c, dan d, dan empat buah sisi berujung ab, ac, ad, dan cd.
Loop
Dalam grafik, jika suatu sisi ditarik dari puncak ke titik itu sendiri, itu disebut putaran.
Example 1

Pada grafik di atas, V adalah puncak yang memiliki tepi (V, V) yang membentuk lingkaran.
Example 2

Pada graf ini terdapat dua simpul yang terbentuk pada simpul a dan simpul b.
Derajat Vertex
Ini adalah jumlah simpul yang berdekatan dengan simpul V.
Notation - derajat (V).
Dalam grafik sederhana dengan n jumlah simpul, derajat dari sembarang simpul adalah -
derajat (v) ≤ n - 1 ∀ v ∈ G
Sebuah simpul dapat membentuk sebuah sisi dengan semua simpul lainnya kecuali dengan sendirinya. Jadi derajat dari sebuah simpul akan naik kenumber of vertices in the graph minus 1. 1 ini untuk self-vertex karena tidak dapat membentuk lingkaran dengan sendirinya. Jika ada loop di salah satu simpul, maka itu bukan Grafik Sederhana.
Derajat simpul dapat dianggap dalam dua kasus grafik -
Grafik Tidak Berarah
Grafik Berarah
Derajat Simpul dalam Graf Tak Berarah
Grafik yang tidak berarah tidak memiliki tepi berarah. Perhatikan contoh berikut.
Example 1
Perhatikan grafik berikut -

Dalam Grafik Tidak Terarah di atas,
derajat (a) = 2, karena ada 2 sisi yang bertemu di simpul 'a'.
derajat (b) = 3, karena ada 3 sisi yang bertemu di simpul 'b'.
derajat (c) = 1, karena ada 1 sisi yang terbentuk di puncak 'c'
Jadi 'c' adalah a pendent vertex.
derajat (d) = 2, karena ada 2 sisi yang bertemu di simpul 'd'.
derajat (e) = 0, karena ada 0 sisi yang terbentuk pada simpul 'e'.
Jadi 'e' adalah isolated vertex.
Example 2
Perhatikan grafik berikut -

Pada grafik di atas,
derajat (a) = 2, derajat (b) = 2, derajat (c) = 2, derajat (d) = 2, dan derajat (e) = 0.
Titik puncak 'e' adalah simpul terisolasi. Grafik tidak memiliki simpul independen.
Derajat Vertex dalam Graf Berarah
Dalam graf berarah, setiap simpul memiliki indegree dan sebuah outdegree.
Indegree dari sebuah Grafik
Indegree dari simpul V adalah banyaknya sisi yang masuk ke simpul V.
Notation - derajat (V).
Outdegree dari sebuah Graph
Derajat keluar dari simpul V adalah banyaknya sisi yang keluar dari simpul V.
Notation - derajat + (V).
Perhatikan contoh berikut.
Example 1
Perhatikan grafik berarah berikut. Vertex 'a' memiliki dua sisi, 'ad' dan 'ab', yang mengarah ke luar. Oleh karena itu outdegree-nya adalah 2. Demikian pula, ada sisi 'ga', menuju simpul 'a'. Karenanya indegree dari 'a' adalah 1.

Indegree dan outdegree dari simpul lain ditunjukkan pada tabel berikut -
| Puncak | Indegree | Derajat lebih tinggi |
|---|---|---|
| Sebuah | 1 | 2 |
| b | 2 | 0 |
| c | 2 | 1 |
| d | 1 | 1 |
| e | 1 | 1 |
| f | 1 | 1 |
| g | 0 | 2 |
Example 2
Perhatikan grafik berarah berikut. Simpul 'a' memiliki tepi 'ae' keluar dari simpul 'a'. Karenanya outdegree-nya adalah 1. Demikian pula, graf tersebut memiliki tepi 'ba' yang mengarah ke simpul 'a'. Karenanya indegree dari 'a' adalah 1.

Indegree dan outdegree dari simpul lain ditunjukkan pada tabel berikut -
| Puncak | Indegree | Derajat lebih tinggi |
|---|---|---|
| Sebuah | 1 | 1 |
| b | 0 | 2 |
| c | 2 | 0 |
| d | 1 | 1 |
| e | 1 | 1 |
Vertex Independen
Dengan menggunakan derajat dari sebuah simpul, kita memiliki dua tipe simpul khusus. Sebuah simpul dengan derajat satu disebut simpul independen.
Example

Di sini, dalam contoh ini, simpul 'a' dan simpul 'b' memiliki tepi yang terhubung 'ab'. Jadi sehubungan dengan simpul 'a', hanya ada satu sisi menuju simpul 'b' dan demikian pula dengan simpul 'b', hanya ada satu sisi menuju simpul 'a'. Akhirnya, simpul 'a' dan simpul 'b' memiliki derajat sebagai satu yang disebut juga sebagai simpul independen.
Vertex Terisolasi
Sebuah simpul dengan derajat nol disebut simpul terisolasi.
Example

Di sini, simpul 'a' dan simpul 'b' tidak memiliki hubungan satu sama lain dan juga ke simpul lainnya. Jadi derajat kedua simpul 'a' dan 'b' adalah nol. Ini juga disebut sebagai simpul terisolasi.
Kedekatan
Berikut adalah norma kedekatan -
Dalam sebuah graf, dikatakan dua simpul adjacent, jika ada tepi di antara dua simpul. Di sini, ketetanggaan simpul dipertahankan oleh satu sisi yang menghubungkan kedua simpul tersebut.
Dalam sebuah graf, dua sisi dikatakan bersebelahan, jika terdapat titik sudut yang sama di antara kedua sisi tersebut. Di sini, ketetanggaan tepi dipertahankan oleh simpul tunggal yang menghubungkan dua sisi.
Example 1
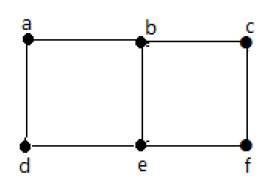
Pada grafik di atas -
'a' dan 'b' adalah simpul yang berdekatan, karena ada tepi yang sama 'ab' di antara keduanya.
'a' dan 'd' adalah simpul yang berdekatan, karena ada tepi yang sama 'ad' di antara keduanya.
ab 'dan' be 'adalah tepi yang berdekatan, karena ada titik sudut' b 'yang sama di antara keduanya.
be 'dan' de 'adalah tepi yang berdekatan, karena ada titik sudut' e 'yang sama di antara keduanya.
Example 2
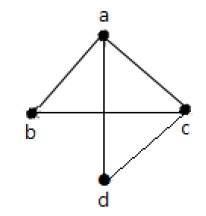
Pada grafik di atas -
'a' dan 'd' adalah simpul yang berdekatan, karena ada tepi yang sama 'ad' di antara keduanya.
'c' dan 'b' adalah simpul yang berdekatan, karena ada tepi yang sama 'cb' di antara keduanya.
'ad' dan 'cd' adalah tepi yang berdekatan, karena ada titik 'd' yang sama di antara keduanya.
'ac' dan 'cd' adalah tepi yang berdekatan, karena ada titik 'c' yang sama di antara keduanya.
Tepi Paralel
Dalam sebuah graf, jika sepasang simpul dihubungkan oleh lebih dari satu sisi, maka sisi-sisi tersebut disebut sisi-sisi paralel.
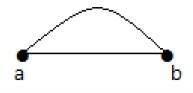
Pada grafik di atas, 'a' dan 'b' adalah dua buah simpul yang dihubungkan oleh dua sisi 'ab' dan 'ab' di antara keduanya. Jadi itu disebut sebagai tepi paralel.
Multi Grafik
Grafik yang memiliki tepi paralel disebut Multigraf.
Example 1

Pada grafik di atas, ada lima sisi 'ab', 'ac', 'cd', 'cd', dan 'bd'. Karena 'c' dan 'd' memiliki dua tepi paralel di antara mereka, itu Multigraph.
Example 2
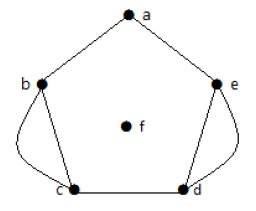
Pada grafik di atas, simpul 'b' dan 'c' memiliki dua sisi. Simpul 'e' dan 'd' juga memiliki dua sisi di antara keduanya. Oleh karena itu, ini adalah Multigraf.
Derajat Urutan Grafik
Jika derajat dari semua simpul pada suatu graf disusun dalam urutan turun atau naik, maka urutan yang diperoleh dikenal sebagai urutan derajat grafik.
Example 1

| Puncak | SEBUAH | b | c | d | e |
|---|---|---|---|---|---|
| Menghubungkan ke | b, c | iklan | iklan | c, b, e | d |
| Gelar | 2 | 2 | 2 | 3 | 1 |
Pada grafik di atas, untuk simpul {d, a, b, c, e}, deret derajatnya adalah {3, 2, 2, 2, 1}.
Example 2

| Puncak | SEBUAH | b | c | d | e | f |
|---|---|---|---|---|---|---|
| Menghubungkan ke | menjadi | a, c | b, d | c, e | iklan | - |
| Gelar | 2 | 2 | 2 | 2 | 2 | 0 |
Pada grafik di atas, untuk simpul {a, b, c, d, e, f}, deret derajatnya adalah {2, 2, 2, 2, 2, 0}.
Grafik dilengkapi dengan berbagai properti yang digunakan untuk karakterisasi grafik tergantung pada strukturnya. Properti ini didefinisikan dalam istilah khusus yang berkaitan dengan domain teori grafik. Pada bab ini, kita akan membahas beberapa properti dasar yang umum pada semua grafik.
Jarak antara Dua Simpul
Ini adalah jumlah sisi pada jalur terpendek antara Simpul U dan Simpul V. Jika ada banyak jalur yang menghubungkan dua simpul, maka jalur terpendek dianggap sebagai jarak antara dua simpul.
Notasi - d (U, V)
Ada sejumlah jalur yang ada dari satu simpul ke simpul lainnya. Di antara itu, Anda hanya perlu memilih yang terpendek.
Example
Perhatikan grafik berikut -

Di sini, jarak dari simpul 'd' ke simpul 'e' atau sederhananya 'de' adalah 1 karena ada satu sisi di antara keduanya. Ada banyak jalur dari simpul 'd' ke simpul 'e' -
- da, ab, be
- df, fg, ge
- de (Ini dianggap untuk jarak antara simpul)
- df, fc, ca, ab, be
- da, ac, cf, fg, ge
Eksentrisitas sebuah Vertex
Jarak maksimum antara simpul ke semua simpul lainnya dianggap sebagai eksentrisitas simpul.
Notasi - e (V)
Jarak dari simpul tertentu ke semua simpul lain dalam grafik diambil dan di antara jarak tersebut, eksentrisitas adalah jarak tertinggi.
Example
Pada grafik di atas, eksentrisitas 'a' adalah 3.
Jarak dari 'a' ke 'b' adalah 1 ('ab'),
dari 'a' ke 'c' adalah 1 ('ac'),
dari 'a' menjadi 'd' adalah 1 ('ad'),
dari 'a' menjadi 'e' adalah 2 ('ab' - 'be') atau ('ad' - 'de'),
dari 'a' ke 'f' adalah 2 ('ac' - 'cf') atau ('ad' - 'df'),
dari 'a' hingga 'g' adalah 3 ('ac' - 'cf' - 'fg') atau ('ad' - 'df' - 'fg').
Jadi eksentrisitasnya adalah 3 yaitu maksimal dari simpul 'a' dari jarak antara 'ag' yang maksimal.
Dengan kata lain,
e (b) = 3
e (c) = 3
e (d) = 2
e (e) = 3
e (f) = 3
e (g) = 3
Radius Grafik Terhubung
Eksentrisitas minimum dari semua simpul dianggap sebagai jari-jari Grafik G.Minimum di antara semua jarak maksimum antara simpul ke semua simpul lainnya dianggap sebagai jari-jari dari Grafik G.
Notasi - r (G)
Dari semua eksentrisitas simpul dalam grafik, jari-jari grafik terhubung adalah minimum dari semua eksentrisitas tersebut.
Example
Pada grafik di atas r (G) = 2, yang merupakan eksentrisitas minimum untuk 'd'.
Diameter Grafik
Eksentrisitas maksimum dari semua simpul dianggap sebagai diameter Grafik G.Maksimum di antara semua jarak antara simpul ke semua simpul lainnya dianggap sebagai diameter Grafik G.
Notation − d(G) - Dari semua eksentrisitas simpul dalam grafik, diameter grafik terhubung adalah maksimum dari semua eksentrisitas tersebut.
Example
Pada grafik di atas, d (G) = 3; yang merupakan eksentrisitas maksimum.
Titik tengah
Jika eksentrisitas grafik sama dengan jari-jarinya, maka grafik tersebut disebut sebagai titik pusat grafik. Jika
e (V) = r (V),
maka 'V' adalah titik pusat dari Grafik 'G'.
Example
Pada grafik contoh, 'd' adalah titik pusat grafik.
e (d) = r (d) = 2
Pusat
Himpunan semua titik pusat 'G' disebut pusat Grafik.
Example
Dalam grafik contoh, {'d'} adalah pusat Grafik.
Lingkar
Itu number of edges in the longest cycle of ‘G’ disebut sebagai keliling 'G'.
Example
Pada grafik contoh, kelilingnya adalah 6, yang kita peroleh dari siklus terpanjang acfgeba atau acfdeba.
Ketebalan
Jumlah edge pada siklus terpendek dari 'G' disebut Girth nya.
Notation: g (G).
Example - Pada graf contoh, lingkar graf adalah 4, yang kita peroleh dari siklus terpendek acfda atau dfged atau abeda.
Jumlah Teorema Derajat Simpul
Jika G = (V, E) adalah graf tidak berarah dengan simpul V = {V 1 , V 2 ,… V n } maka
Corollary 1
Jika G = (V, E) adalah graf berarah dengan simpul V = {V 1 , V 2 ,… V n }, maka
Corollary 2
Dalam graf tidak berarah mana pun, jumlah simpul dengan derajat Ganjil adalah Genap.
Corollary 3
Dalam graf tak berarah, jika derajat tiap simpul adalah k, maka
Corollary 4
Dalam graf tak berarah, jika derajat setiap simpul paling sedikit k, maka
| Corollary 5
Dalam graf tak berarah, jika derajat setiap simpul paling banyak k, maka
Ada berbagai jenis grafik tergantung pada jumlah simpul, jumlah tepi, interkonektivitas, dan struktur keseluruhannya. Kami hanya akan membahas beberapa jenis grafik penting dalam bab ini.
Grafik Null
A graph having no edges disebut Grafik Null.
Contoh

Pada graf di atas, ada tiga simpul bernama 'a', 'b', dan 'c', tetapi tidak ada sisi di antaranya. Oleh karena itu, ini adalah Grafik Null.
Grafik Sepele
SEBUAH graph with only one vertex disebut Grafik Trivial.
Contoh

Pada grafik yang ditunjukkan di atas, hanya ada satu simpul 'a' tanpa tepi lainnya. Oleh karena itu, ini adalah grafik Trivial.
Grafik Tidak Berarah
Grafik tidak berarah mengandung tepi tetapi tepi tidak berarah.
Contoh
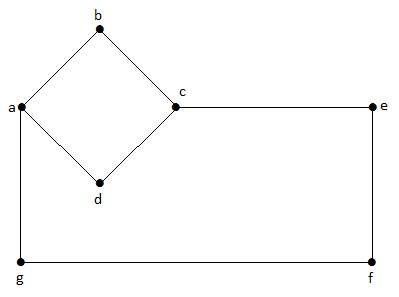
Dalam grafik ini, 'a', 'b', 'c', 'd', 'e', 'f', 'g' adalah simpul, dan 'ab', 'bc', 'cd', 'da ',' ag ',' gf ',' ef 'adalah tepi grafik. Karena ini adalah grafik tidak berarah, tepi 'ab' dan 'ba' sama. Demikian pula tepi lainnya juga dipertimbangkan dengan cara yang sama.
Grafik Berarah
Dalam graf berarah, setiap sisi memiliki arah.
Contoh

Pada grafik di atas, kita memiliki tujuh simpul 'a', 'b', 'c', 'd', 'e', 'f', dan 'g', dan delapan sisi 'ab', 'cb', ' dc ',' ad ',' ec ',' fe ',' gf ', dan' ga '. Karena ini adalah grafik berarah, setiap tepi memiliki tanda panah yang menunjukkan arahnya. Perhatikan bahwa dalam grafik berarah, 'ab' berbeda dari 'ba'.
Grafik Sederhana
Sebuah grafik with no loops dan tidak parallel edges disebut grafik sederhana.
Jumlah maksimum sisi yang mungkin dalam satu graf dengan simpul 'n' adalah n C 2 di mana n C 2 = n (n - 1) / 2.
Banyaknya graf sederhana yang dimungkinkan dengan simpul 'n' = 2 n c 2 = 2 n (n-1) / 2 .
Contoh
Pada graf berikut, terdapat 3 buah simpul dengan 3 buah sisi yang paling banyak tidak termasuk tepi dan simpul paralel. Ini dapat dibuktikan dengan menggunakan rumus di atas.
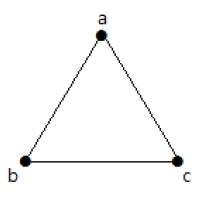
Jumlah maksimum sisi dengan n = 3 simpul -
Jumlah maksimum grafik sederhana dengan n = 3 simpul -
8 grafik ini seperti yang ditunjukkan di bawah ini -
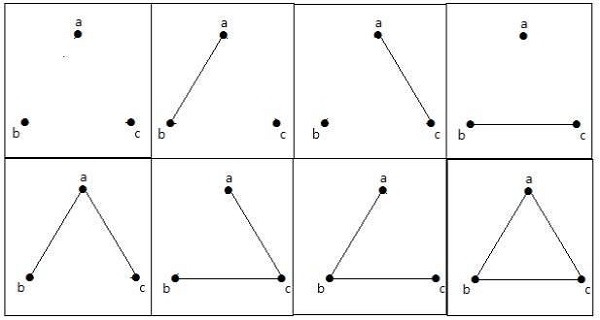
Grafik Terhubung
Grafik G dikatakan terhubung if there exists a path between every pair of vertices. Harus ada setidaknya satu sisi untuk setiap simpul di grafik. Sehingga kita dapat mengatakan bahwa itu terhubung ke beberapa simpul lain di sisi lain tepi.
Contoh
Pada graf berikut, setiap simpul memiliki sisi yang terhubung ke sisi lainnya. Karenanya ini adalah grafik yang terhubung.

Grafik Terputus
Grafik G terputus, jika tidak mengandung setidaknya dua simpul yang terhubung.
Contoh 1
Grafik berikut adalah contoh Graph Terputus, dimana terdapat dua komponen, satu dengan 'a', 'b', 'c', 'd' vertices dan lainnya dengan 'e', 'f', 'g', simpul 'h'.
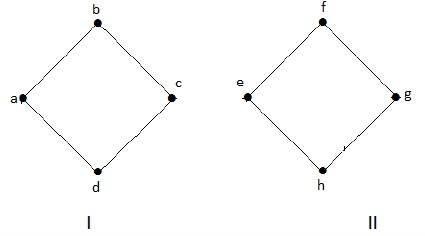
Kedua komponen tersebut berdiri sendiri dan tidak terhubung satu sama lain. Karenanya ini disebut grafik terputus.
Contoh 2

Dalam contoh ini, terdapat dua komponen independen, abfe dan cd, yang tidak terhubung satu sama lain. Karenanya ini adalah grafik terputus.
Grafik Reguler
Grafik G dikatakan teratur, if all its vertices have the same degree. Dalam suatu graf, jika derajat setiap simpul adalah 'k', maka graf tersebut disebut dengan 'graf beraturan k'.
Contoh
Pada grafik berikut, semua simpul memiliki derajat yang sama. Jadi grafik ini disebut grafik biasa.
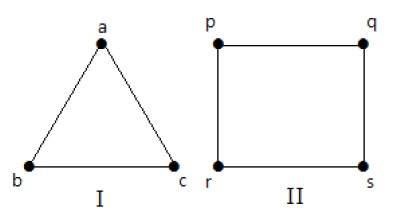
Pada kedua grafik, semua simpul memiliki derajat 2. Mereka disebut Graf 2-Reguler.
Grafik Lengkap
Grafik sederhana dengan simpul bersama 'n' disebut grafik lengkap dan memang demikian denoted by ‘Kn’. Dalam grafik,a vertex should have edges with all other vertices, lalu disebut grafik lengkap.
Dengan kata lain, jika satu simpul terhubung ke semua simpul lain dalam sebuah graf, maka itu disebut graf lengkap.
Contoh
Pada grafik berikut, setiap simpul dalam grafik terhubung dengan semua simpul yang tersisa dalam grafik kecuali dengan simpul itu sendiri.
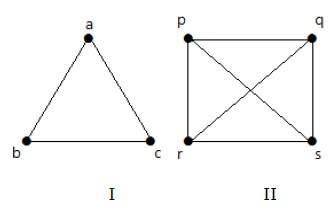
Dalam grafik I,
| Sebuah | b | c | |
|---|---|---|---|
| Sebuah | Tidak terhubung | Terhubung | Terhubung |
| b | Terhubung | Tidak terhubung | Terhubung |
| c | Terhubung | Terhubung | Tidak terhubung |
Pada grafik II,
| p | q | r | s | |
|---|---|---|---|---|
| p | Tidak terhubung | Terhubung | Terhubung | Terhubung |
| q | Terhubung | Tidak terhubung | Terhubung | Terhubung |
| r | Terhubung | Terhubung | Tidak terhubung | Terhubung |
| s | Terhubung | Terhubung | Terhubung | Tidak terhubung |
Grafik Siklus
Graf sederhana dengan simpul 'n' (n> = 3) dan sisi 'n' disebut graf siklus jika semua sisinya membentuk siklus dengan panjang 'n'.
Jika derajat setiap simpul pada graf tersebut adalah dua, maka graf tersebut disebut Graf Siklus.
Notation- C n
Contoh
Perhatikan grafik berikut -
Grafik I memiliki 3 buah simpul dengan 3 buah sisi yang membentuk siklus 'ab-bc-ca'.
Grafik II memiliki 4 buah simpul dengan 4 buah sisi yang membentuk sebuah lingkaran 'pq-qs-sr-rp'.
Grafik III memiliki 5 buah simpul dengan 5 sisi yang membentuk sebuah lingkaran 'ik-km-ml-lj-ji'.

Oleh karena itu semua grafik yang diberikan adalah grafik siklus.
Grafik Roda
Grafik roda diperoleh dari grafik siklus C n-1 dengan menambahkan simpul baru. Simpul baru itu disebut aHubyang terhubung ke semua simpul dari C n .
Notasi - W n
Jumlah tepi di W n = Jumlah tepi dari hub ke semua simpul lainnya +
Jumlah tepi dari semua node lain dalam grafik siklus tanpa hub.
= (n – 1) + (n – 1)
= 2 (n – 1)
Contoh
Perhatikan grafik berikut. Semuanya adalah grafik roda.
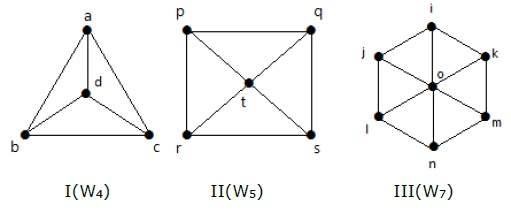
Dalam grafik I, ini diperoleh dari C 3 dengan menambahkan titik di tengah yang dinamai 'd'. Ini dilambangkan sebagai W 4 .
Jumlah tepi di W4 = 2 (n-1) = 2 (3) = 6
Dalam grafik II, diperoleh dari C4 dengan menambahkan titik di tengah yang dinamai 't'. Ini dilambangkan sebagai W 5 .
Jumlah sisi di W5 = 2 (n-1) = 2 (4) = 8
Dalam grafik III, diperoleh dari C 6 dengan menambahkan titik di tengah yang disebut 'o'. Ini dilambangkan sebagai W 7 .
Jumlah tepi di W4 = 2 (n-1) = 2 (6) = 12
Grafik Siklik
Sebuah grafik with at least one siklus ini disebut grafik siklik.
Contoh
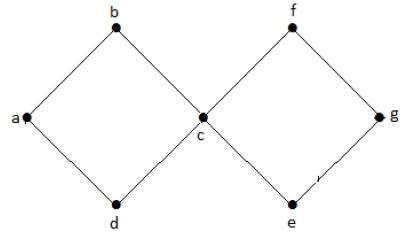
Pada grafik contoh di atas, kami memiliki dua siklus abcda dan cfgec. Karenanya ini disebut grafik siklik.
Grafik Asiklik
Sebuah grafik with no cycles disebut grafik asiklik.
Contoh
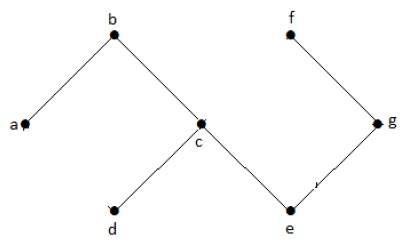
Dalam grafik contoh di atas, kami tidak memiliki siklus apa pun. Karenanya ini adalah grafik non-siklik.
Graf Bipartit
Graf sederhana G = (V, E) dengan sekat simpul V = {V 1 , V 2 } disebut graf bipartitif every edge of E joins a vertex in V1 to a vertex in V2.
Secara umum, graf bipertit memiliki dua himpunan simpul, katakanlah, V1 dan V2, dan jika sebuah sisi digambar, ia harus menghubungkan sembarang simpul di himpunan V 1 ke sembarang simpul di himpunan V 2 .
Contoh
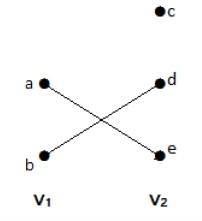
Dalam grafik ini, Anda dapat mengamati dua set simpul - V 1 dan V 2 . Di sini, dua sisi bernama 'ae' dan 'bd' menghubungkan simpul dari dua himpunan V 1 dan V 2 .
Grafik Bipartit Lengkap
Graf bipartit 'G', G = (V, E) dengan partisi V = {V 1 , V 2 } dikatakan graf bipartit lengkap jika setiap simpul di V 1 terhubung ke setiap simpul dari V 2 .
Secara umum, graf bipartit lengkap menghubungkan setiap simpul dari himpunan V 1 ke tiap simpul dari himpunan V 2 .
Contoh
Graf berikut merupakan graf bipartit lengkap karena memiliki tepi yang menghubungkan setiap simpul dari himpunan V 1 ke setiap simpul dari himpunan V 2 .
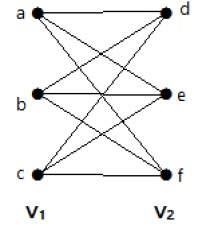
Jika | V 1 | = m dan | V 2 | = n, maka graf bipartit lengkap dilambangkan dengan K m, n .
- K m, n memiliki (m + n) simpul dan (mn) sisi.
- K m, n adalah graf beraturan jika m = n.
Secara umum, a complete bipartite graph is not a complete graph.
K m, n adalah graf lengkap jika m = n = 1.
Jumlah maksimum sisi dalam graf bipartit dengan n simpul adalah -
[n 2 /4] Dunia
Jika n = 10, k5, 5 = [n2 / 4] = [10 2 /4] = 25.
Begitu pula dengan K6, 4 = 24
K7, 3 = 21
K8, 2 = 16
K9, 1 = 9
Jika n = 9, k5, 4 = [n2 / 4] = [92/4] = 20
Begitu pula dengan K6, 3 = 18
K7, 2 = 14
K8, 1 = 8
'G' adalah graf bipartit jika 'G' tidak memiliki siklus dengan panjang ganjil. Kasus khusus dari grafik bipartit adalah grafik bintang.
Grafik Bintang
Graf bipartit lengkap berbentuk K1, n-1 adalah graf bintang dengan n-simpul. Grafik bintang adalah grafik bipartit lengkap jika satu simpul milik satu himpunan dan semua simpul yang tersisa milik himpunan lainnya.
Contoh
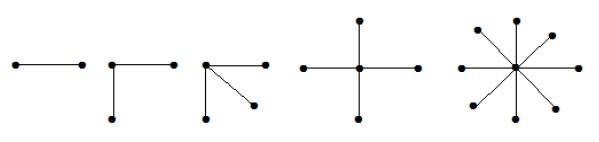
Pada grafik di atas, dari simpul 'n', semua simpul 'n – 1' terhubung ke sebuah simpul tunggal. Oleh karena itu dalam bentuk K 1 , n-1 yang star grafik.
Pelengkap Grafik
Misalkan 'G−' adalah graf sederhana dengan beberapa simpul seperti pada 'G' dan sebuah sisi {U, V} hadir dalam 'G−', jika sisi tersebut tidak ada di G. Artinya, dua simpul bersebelahan di 'G−' jika dua simpul tidak berdekatan di G.
Jika tepi-tepi yang ada pada graf I tidak ada pada graf II yang lain, dan jika graf I dan graf II digabungkan menjadi satu membentuk graf utuh, maka graf I dan graf II disebut saling melengkapi.
Contoh
Dalam contoh berikut, grafik-I memiliki dua sisi 'cd' dan 'bd'. Grafik komplemen-II memiliki empat sisi.
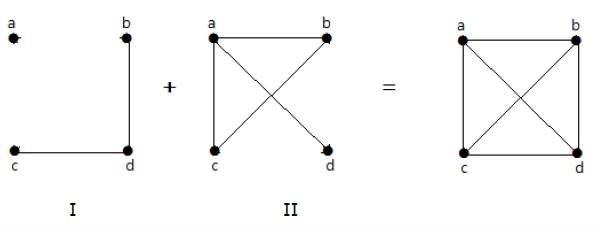
Perhatikan bahwa tepi pada grafik-I tidak ada pada grafik-II dan sebaliknya. Oleh karena itu, kombinasi dari kedua grafik tersebut menghasilkan grafik simpul 'n' yang lengkap.
Note - Kombinasi dua grafik pelengkap menghasilkan grafik yang lengkap.
Jika 'G' adalah grafik sederhana, maka
| E (G) | + | E ('G -') | = | E (Kn) |, di mana n = jumlah simpul pada grafik.
Contoh
Misalkan 'G' menjadi grafik sederhana dengan sembilan simpul dan dua belas sisi, temukan jumlah sisi di 'G-'.
Anda memiliki, | E (G) | + | E ('G -') | = | E (Kn) |
12 + | E ('G -') | =
9 (9-1) / 2 = 9 C 2
12 + | E ('G -') | = 36
| E ('G -') | = 24
'G' adalah grafik sederhana dengan 40 sisi dan komplemennya 'G−' memiliki 38 sisi. Temukan jumlah simpul pada grafik G atau 'G−'.
Misalkan jumlah simpul pada grafik menjadi 'n'.
Kami memiliki, | E (G) | + | E ('G -') | = | E (Kn) |
40 + 38 = n (n-1) / 2
156 = n (n-1)
13 (12) = n (n-1)
n = 13
Pohon adalah grafik yang tidak mengandung satu siklus pun. Mereka mewakili struktur hierarki dalam bentuk grafik. Pohon termasuk dalam kelas grafik yang paling sederhana. Terlepas dari kesederhanaannya, mereka memiliki struktur yang kaya.
Pohon menyediakan berbagai aplikasi berguna, mulai dari pohon keluarga hingga serumit pohon dalam struktur data ilmu komputer.
Pohon
SEBUAH connected acyclic graphdisebut pohon. Dengan kata lain, graf terhubung tanpa siklus disebut pohon.
Tepi pohon dikenal sebagai branches. Elemen pohon disebut simpul mereka. Node tanpa node turunan disebutleaf nodes.
Sebuah pohon dengan simpul 'n' memiliki tepi 'n-1'. Jika ia memiliki satu tepi lebih banyak dari 'n-1', maka tepi ekstra tersebut jelas harus berpasangan dengan dua simpul yang mengarah untuk membentuk sebuah siklus. Kemudian menjadi grafik siklik yang merupakan pelanggaran bagi grafik pohon.
Example 1
Grafik yang ditampilkan di sini adalah pohon karena tidak memiliki siklus dan terhubung. Ia memiliki empat simpul dan tiga sisi, yaitu, untuk tepi 'n' simpul 'n-1' seperti yang disebutkan dalam definisi.
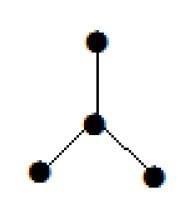
Note - Setiap pohon memiliki setidaknya dua simpul berderajat satu.
Example 2
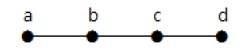
Dalam contoh di atas, simpul 'a' dan 'd' memiliki derajat satu. Dan dua simpul lainnya 'b' dan 'c' memiliki derajat dua. Ini dimungkinkan karena untuk tidak membentuk siklus, harus ada setidaknya dua sisi tunggal di manapun dalam grafik. Itu tidak lain adalah dua sisi dengan derajat satu.
Hutan
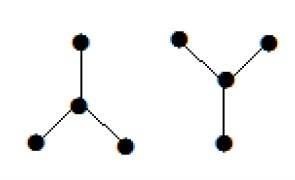
SEBUAH disconnected acyclic graphdisebut hutan. Dengan kata lain, kumpulan pohon yang terputus-putus disebut hutan.
Example
Grafik berikut terlihat seperti dua sub-grafik; tetapi ini adalah grafik tunggal yang tidak terhubung. Tidak ada siklus dalam grafik ini. Oleh karena itu, jelas itu adalah hutan.
Merentang Pohon
Misalkan G adalah graf terhubung, maka sub-graf H dari G disebut pohon rentang dari G jika -
- H adalah pohon
- H berisi semua simpul G.
Pohon rentang T dari graf tak berarah G adalah subgrafik yang mencakup semua simpul G.
Example

Dalam contoh di atas, G adalah graf terhubung dan H adalah sub-graf dari G.
Jelasnya, graf H tidak memiliki siklus, ini adalah sebuah pohon dengan enam sisi yang kurang satu dari jumlah total simpul. Oleh karena itu H adalah pohon Rentang dari G.
Peringkat Sirkuit
Misalkan 'G' adalah grafik yang terhubung dengan 'n' simpul dan tepi 'm'. Pohon rentang 'T' dari G berisi (n-1) tepi.
Oleh karena itu, jumlah tepi yang perlu Anda hapus dari 'G' untuk mendapatkan pohon rentang = m- (n-1), yang disebut peringkat sirkuit G.
Rumus ini benar, karena dalam pohon bentang Anda harus memiliki tepi 'n-1'. Dari tepi 'm', Anda perlu mempertahankan tepi 'n – 1' dalam grafik.
Oleh karena itu, menghapus tepi 'n – 1' dari 'm' memberikan tepi yang akan dihilangkan dari grafik untuk mendapatkan pohon rentang, yang seharusnya tidak membentuk siklus.
Example
Perhatikan grafik berikut -
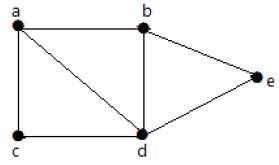
Untuk grafik yang diberikan pada contoh di atas, Anda memiliki m = 7 sisi dan n = 5 simpul.
Maka peringkat sirkuitnya adalah -
Example
Misalkan 'G' adalah graf terhubung dengan enam simpul dan derajat dari setiap simpul adalah tiga. Temukan peringkat sirkuit 'G'.
Dengan jumlah teorema derajat simpul,
Teorema Kirchoff
Teorema Kirchoff berguna untuk mencari jumlah pohon merentang yang dapat dibentuk dari graf terhubung.
Example
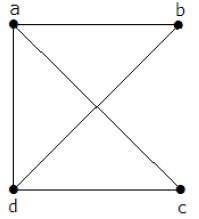
Matriks 'A' diisi seperti, jika ada tepi di antara dua simpul, maka harus diberikan sebagai '1', jika tidak '0'.
$$A=\begin{vmatrix}0 & a & b & c & d\\a & 0 & 1 & 1 & 1 \\b & 1 & 0 & 0 & 1\\c & 1 & 0 & 0 & 1\\d & 1 & 1 & 1 & 0 \end{vmatrix} = \begin{vmatrix} 0 & 1 & 1 & 1\\1 & 0 & 0 & 1\\1 & 0 & 0 & 1\\1 & 1 & 1 & 0\end{vmatrix}$$Dengan menggunakan teorema kirchoff, itu harus diubah dengan mengganti nilai diagonal prinsip dengan derajat simpul dan semua elemen lainnya dengan -1.
$$=\begin{vmatrix} 3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix}=M$$ $$M=\begin{vmatrix}3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix} =8$$ $$Co\:\:factor\:\:of\:\:m1\:\:= \begin{vmatrix} 2 & 0 & -1\\0 & 2 & -1\\-1 & -1 & 3\end{vmatrix}$$Jadi, jumlah pohon merentang = 8.
Apakah mungkin untuk melintasi suatu graf dari satu simpul ke simpul lainnya ditentukan oleh bagaimana sebuah graf terhubung. Konektivitas adalah konsep dasar dalam Teori Graf. Konektivitas menentukan apakah grafik terhubung atau terputus. Ini memiliki subtopik berdasarkan edge dan vertex, yang dikenal sebagai konektivitas tepi dan konektivitas vertex. Mari kita bahas secara detail.
Konektivitas
Sebuah grafik dikatakan connected if there is a path between every pair of vertex. Dari setiap simpul ke simpul lain, harus ada beberapa jalur untuk dilintasi. Itu disebut konektivitas grafik. Sebuah grafik dengan beberapa simpul dan tepi terputus dikatakan terputus.
Example 1
Pada grafik berikut, dimungkinkan untuk melakukan perjalanan dari satu simpul ke simpul lainnya. Misalnya, seseorang dapat melintasi dari simpul 'a' ke simpul 'e' menggunakan jalur 'ab-e'.
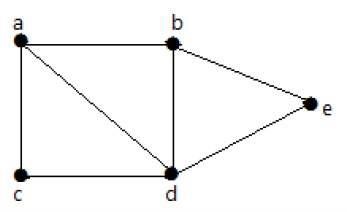
Example 2
Dalam contoh berikut, berpindah dari simpul 'a' ke simpul 'f' tidak dimungkinkan karena tidak ada jalur di antara keduanya secara langsung atau tidak langsung. Karenanya ini adalah grafik yang terputus.
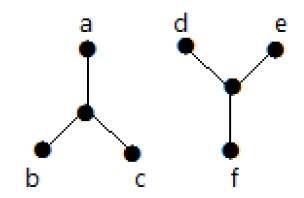
Potong Vertex
Misalkan 'G' adalah grafik yang terhubung. Sebuah simpul V ∈ G disebut simpul potong dari 'G', jika 'G-V' (Hapus 'V' dari 'G') menghasilkan graf yang terputus. Menghapus titik potong dari grafik akan memecahnya menjadi dua grafik atau lebih.
Note - Menghapus titik potong dapat membuat grafik terputus.
Sebuah graf terhubung 'G' mungkin memiliki paling banyak (n – 2) simpul yang dipotong.
Example
Pada grafik berikut, simpul 'e' dan 'c' adalah simpul yang dipotong.

Dengan menghilangkan 'e' atau 'c', grafik akan menjadi grafik yang terputus.

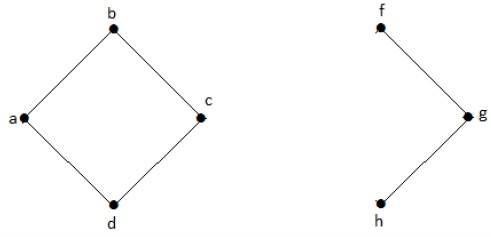
Tanpa 'g', tidak ada jalur antara simpul 'c' dan simpul 'h' dan banyak lainnya. Oleh karena itu, ini adalah grafik yang terputus dengan simpul potong sebagai 'e'. Demikian pula, 'c' juga merupakan titik potong untuk graf di atas.
Cut Edge (Bridge)
Misalkan 'G' adalah grafik yang terhubung. Sisi 'e' ∈ G disebut sebagai tepi potong jika 'G-e' menghasilkan grafik yang tidak terhubung.
Jika menghilangkan tepi dalam grafik menghasilkan dua atau lebih grafik, maka tepi itu disebut Tepi Potong.
Example
Pada grafik berikut, tepi potongnya adalah [(c, e)].

Dengan menghilangkan tepi (c, e) dari grafik, itu menjadi grafik yang terputus.


Pada grafik di atas, menghilangkan sisi (c, e) memecah grafik menjadi dua yang tidak lain adalah grafik yang terputus. Oleh karena itu, tepi (c, e) adalah tepi potong pada grafik.
Note - Misalkan 'G' adalah graf terhubung dengan simpul 'n', lalu
tepi potong e ∈ G jika dan hanya jika tepi 'e' bukan bagian dari siklus apa pun di G.
jumlah maksimum tepi potong yang memungkinkan adalah 'n-1'.
setiap kali ada tepi potong, simpul potong juga ada karena setidaknya satu simpul dari sisi potong adalah simpul potong.
jika ada titik potong, maka ujung potong mungkin ada atau tidak.
Potong Set Grafik
Misalkan 'G' = (V, E) adalah grafik yang terhubung. Himpunan bagian E 'dari E disebut himpunan potongan G jika penghapusan semua tepi E' dari G membuat G terputus.
Jika menghapus sejumlah tepi tertentu dari grafik membuatnya terputus, maka tepi yang dihapus tersebut disebut set potong grafik.
Example
Perhatikan grafik berikut. Set potongannya adalah E1 = {e1, e3, e5, e8}.
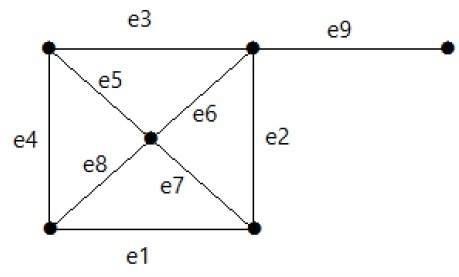
Setelah menghapus set cut E1 dari grafik, akan muncul sebagai berikut -
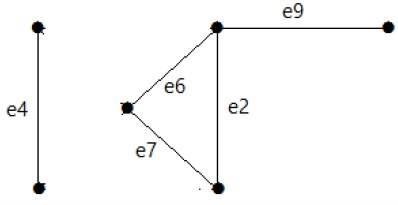
Demikian pula, ada set potongan lain yang dapat memutuskan grafik -
E3 = {e9} - Kumpulan grafik terkecil.
E4 = {e3, e4, e5}
Konektivitas Tepi
Misalkan 'G' adalah grafik yang terhubung. Jumlah minimum tepi yang pemindahannya membuat 'G' terputus disebut konektivitas tepi G.
Notation - λ (G)
Dengan kata lain, file number of edges in a smallest cut set of G disebut konektivitas tepi G.
Jika 'G' memiliki cut edge, maka λ (G) adalah 1. (konektivitas edge G.)
Example
Perhatikan grafik berikut. Dengan menghilangkan dua tepi minimum, grafik yang terhubung menjadi terputus. Sehingga konektivitas edge-nya (λ (G)) adalah 2.
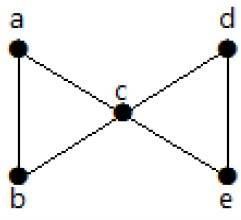
Berikut adalah empat cara untuk memutuskan grafik dengan menghilangkan dua sisi -

Konektivitas Vertex
Misalkan 'G' adalah grafik yang terhubung. Jumlah minimum simpul yang penghapusannya membuat 'G' terputus atau mengurangi 'G' menjadi grafik trivial disebut konektivitas simpulnya.
Notation - K (G)
Example
Pada grafik di atas, menghilangkan simpul 'e' dan 'i' membuat grafik terputus.

Jika G memiliki titik potong, maka K (G) = 1.
Notation - Untuk setiap grafik G yang terhubung,
K (G) ≤ λ (G) ≤ δ (G)
Konektivitas simpul (K (G)), konektivitas tepi (λ (G)), jumlah minimum derajat G (δ (G)).
Example
Hitung λ (G) dan K (G) untuk grafik berikut -
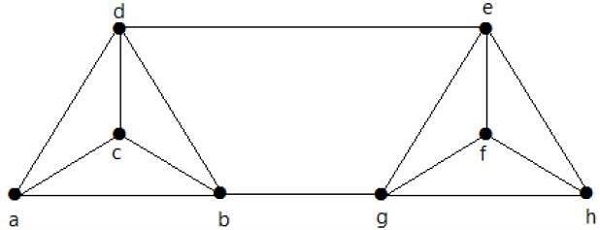
Solution
Dari grafik,
δ (G) = 3
K (G) ≤ λ (G) ≤ δ (G) = 3 (1)
K (G) ≥ 2 (2)
Menghapus tepi {d, e} dan {b, h}, kita dapat memutuskan G.
Karena itu,
λ (G) = 2
2 ≤ λ (G) ≤ δ (G) = 2 (3)
Dari (2) dan (3), konektivitas simpul K (G) = 2
Grafik penutup adalah subgraf yang berisi semua simpul atau semua sisi yang berhubungan dengan graf lain. Sebuah subgrafik yang berisi semua simpul disebut aline/edge covering. Sebuah subgrafik yang berisi semua tepi disebut avertex covering.
Penutup Garis
Misalkan G = (V, E) adalah grafik. Himpunan bagian C (E) disebut garis yang menutupi G jika setiap simpul dari G bersisian dengan setidaknya satu sisi di C, yaitu,
derajat (V) ≥ 1 ∀ V ∈ G
karena setiap simpul terhubung dengan simpul lain oleh sebuah sisi. Oleh karena itu memiliki derajat minimal 1.
Example
Perhatikan grafik berikut -
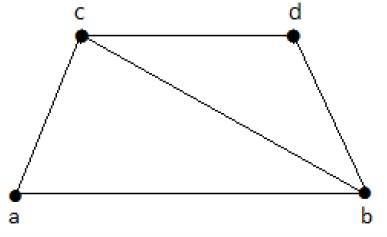
Subgrafinya yang memiliki penutup garis adalah sebagai berikut -
C 1 = {{a, b}, {c, d}}
C 2 = {{a, d}, {b, c}}
C 3 = {{a, b}, {b, c}, {b, d}}
C 4 = {{a, b}, {b, c}, {c, d}}
Penutupan garis 'G' tidak ada jika dan hanya jika 'G' memiliki simpul terisolasi. Penutupan garis dari grafik dengan simpul 'n' memiliki setidaknya [n / 2] sisi.
Minimal Line Covering
Sebuah garis yang menutupi C dari grafik G dikatakan minimal if no edge can be deleted from C.
Example
Pada grafik di atas, subgraf yang memiliki penutup garis adalah sebagai berikut:
C 1 = {{a, b}, {c, d}}
C 2 = {{a, d}, {b, c}}
C 3 = {{a, b}, {b, c}, {b, d}}
C 4 = {{a, b}, {b, c}, {c, d}}
Di sini C 1 , C 2 , C 3 adalah penutup garis minimal, sedangkan C 4 bukan karena kita bisa menghapus {b, c}.
Penutupan Garis Minimum
Itu juga dikenal sebagai Smallest Minimal Line Covering. Penutupan garis minimal dengan jumlah tepi minimum disebut penutup garis minimum 'G'. Jumlah tepi dalam garis minimum yang menutupi di 'G' disebutline covering numberdari 'G' (α 1 ).
Example
Dalam contoh di atas, C 1 dan C 2 adalah garis penutup minimum dari G dan α 1 = 2.
Setiap penutup garis mengandung penutup garis minimal.
Setiap penutup garis tidak mengandung penutup garis minimum (C 3 tidak mengandung penutup garis minimum.
Tidak ada penutup garis minimal yang mengandung siklus.
Jika suatu garis yang menutupi 'C' tidak memiliki jalur dengan panjang 3 atau lebih, maka 'C' adalah garis penutup minimal karena semua komponen 'C' adalah grafik bintang dan dari grafik bintang, tidak ada tepi yang dapat dihapus.
Vertex Covering
Misalkan 'G' = (V, E) menjadi grafik. Himpunan bagian K dari V disebut simpul yang menutupi 'G', jika setiap tepi 'G' bersisian dengan atau ditutupi oleh simpul di 'K'.
Example
Perhatikan grafik berikut -
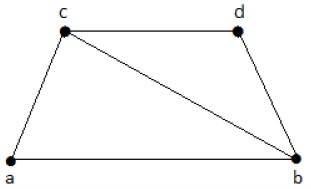
Subgrafik yang dapat diturunkan dari grafik di atas adalah sebagai berikut -
K 1 = {b, c}
K 2 = {a, b, c}
K 3 = {b, c, d}
K 4 = {a, d}
Di sini, K 1 , K 2 , dan K 3 memiliki simpul yang menutupi, sedangkan K 4 tidak memiliki simpul yang menutupi karena tidak menutupi tepi {bc}.
Minimal Vertex Covering
Sebuah simpul 'K' dari graf 'G' dikatakan sebagai simpul minimal yang menutupi jika tidak ada simpul yang dapat dihapus dari 'K'.
Example
Pada grafik di atas, subgrafik yang memiliki penutup puncak adalah sebagai berikut -
K 1 = {b, c}
K 2 = {a, b, c}
K 3 = {b, c, d}
Di sini, K 1 dan K 2 adalah penutup simpul minimal, sedangkan pada K 3 , simpul 'd' bisa dihapus.
Penutupan Vertex Minimum
Ia juga dikenal sebagai penutup simpul minimal terkecil. Sebuah simpul minimal yang menutupi graf 'G' dengan jumlah simpul minimal disebut penutup simpul minimum.
Jumlah simpul pada simpul minimal yang menutupi 'G' disebut simpul yang menutupi bilangan G (α 2 ).
Example
In the following graph, the subgraphs having vertex covering are as follows −
K1 = {b, c}
K2 = {a, b, c}
K3 = {b, c, d}

Here, K1 is a minimum vertex cover of G, as it has only two vertices. α2 = 2.
A matching graph is a subgraph of a graph where there are no edges adjacent to each other. Simply, there should not be any common vertex between any two edges.
Matching
Let ‘G’ = (V, E) be a graph. A subgraph is called a matching M(G), if each vertex of G is incident with at most one edge in M, i.e.,
deg(V) ≤ 1 ∀ V ∈ G
which means in the matching graph M(G), the vertices should have a degree of 1 or 0, where the edges should be incident from the graph G.
Notation − M(G)
Example
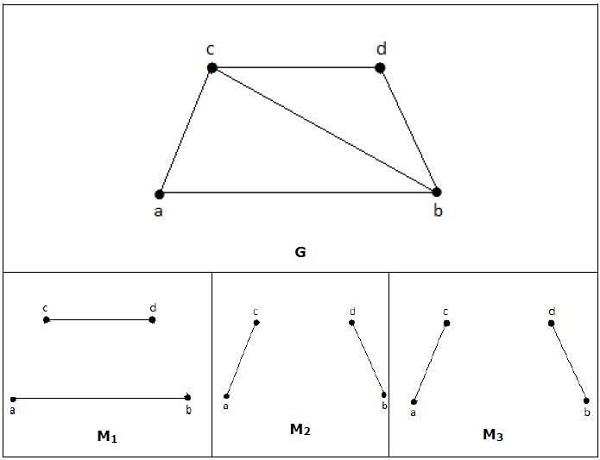

In a matching,
if deg(V) = 1, then (V) is said to be matched
if deg(V) = 0, then (V) is not matched.
In a matching, no two edges are adjacent. It is because if any two edges are adjacent, then the degree of the vertex which is joining those two edges will have a degree of 2 which violates the matching rule.
Maximal Matching
A matching M of graph ‘G’ is said to maximal if no other edges of ‘G’ can be added to M.
Example

M1, M2, M3 from the above graph are the maximal matching of G.
Maximum Matching
It is also known as largest maximal matching. Maximum matching is defined as the maximal matching with maximum number of edges.
The number of edges in the maximum matching of ‘G’ is called its matching number.
Example
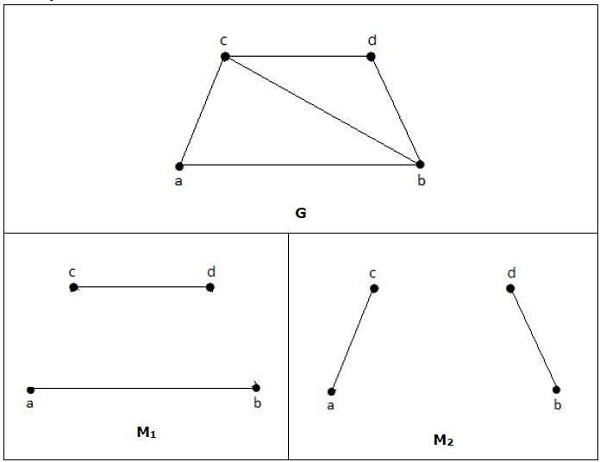
For a graph given in the above example, M1 and M2 are the maximum matching of ‘G’ and its matching number is 2. Hence by using the graph G, we can form only the subgraphs with only 2 edges maximum. Hence we have the matching number as two.
Perfect Matching
A matching (M) of graph (G) is said to be a perfect match, if every vertex of graph g (G) is incident to exactly one edge of the matching (M), i.e.,
deg(V) = 1 ∀ V
The degree of each and every vertex in the subgraph should have a degree of 1.
Example
In the following graphs, M1 and M2 are examples of perfect matching of G.
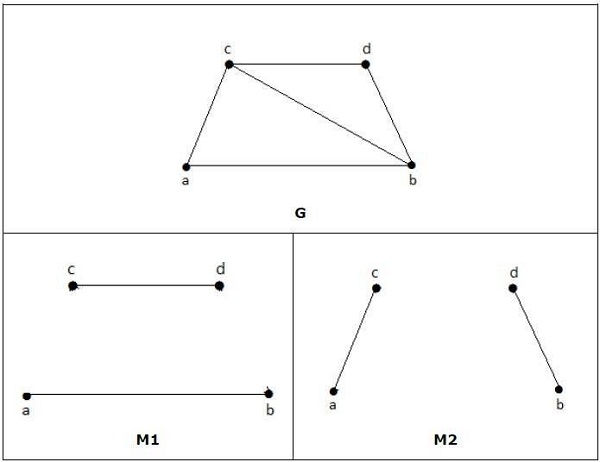
Note − Every perfect matching of graph is also a maximum matching of graph, because there is no chance of adding one more edge in a perfect matching graph.
A maximum matching of graph need not be perfect. If a graph ‘G’ has a perfect match, then the number of vertices |V(G)| is even. If it is odd, then the last vertex pairs with the other vertex, and finally there remains a single vertex which cannot be paired with any other vertex for which the degree is zero. It clearly violates the perfect matching principle.
Example
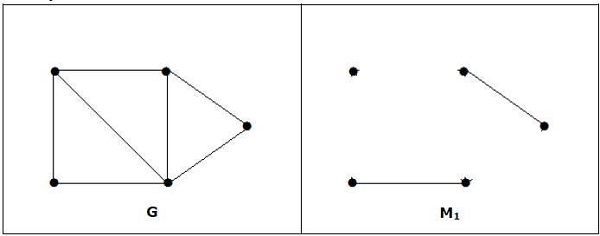
Note − The converse of the above statement need not be true. If G has even number of vertices, then M1 need not be perfect.
Example
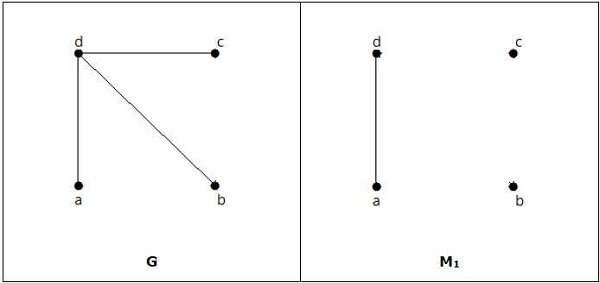
It is matching, but it is not a perfect match, even though it has even number of vertices.
Independent sets are represented in sets, in which
there should not be any edges adjacent to each other. There should not be any common vertex between any two edges.
there should not be any vertices adjacent to each other. There should not be any common edge between any two vertices.
Independent Line Set
Let ‘G’ = (V, E) be a graph. A subset L of E is called an independent line set of ‘G’ if no two edges in L are adjacent. Such a set is called an independent line set.
Example
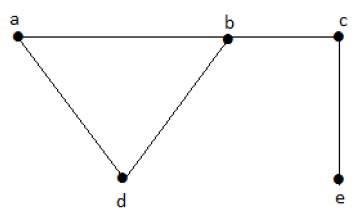
Let us consider the following subsets −
L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}In this example, the subsets L2 and L3 are clearly not the adjacent edges in the given graph. They are independent line sets. However L1 is not an independent line set, as for making an independent line set, there should be at least two edges.
Maximal Independent Line Set
An independent line set is said to be the maximal independent line set of a graph ‘G’ if no other edge of ‘G’ can be added to ‘L’.
Example
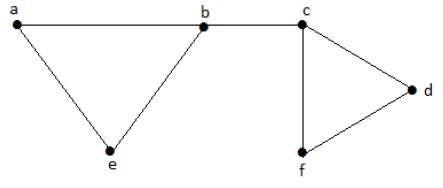
Let us consider the following subsets −
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}L2 and L3 are maximal independent line sets/maximal matching. As for only these two subsets, there is no chance of adding any other edge which is not an adjacent. Hence these two subsets are considered as the maximal independent line sets.
Maximum Independent Line Set
A maximum independent line set of ‘G’ with maximum number of edges is called a maximum independent line set of ‘G’.
Number of edges in a maximum independent line set of G (β1)
= Line independent number of G
= Matching number of GExample
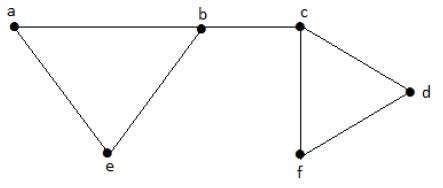
Let us consider the following subsets −
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}L3 is the maximum independent line set of G with maximum edges which are not the adjacent edges in graph and is denoted by β1 = 3.
Note − For any graph G with no isolated vertex,
α1 + β1 = number of vertices in a graph = |V|
Example
Line covering number of Kn/Cn/wn,
$$\alpha 1 = \lceil\frac{n}{2}\rceil\begin{cases}\frac{n}{2}\:if\:n\:is\:even \\\frac{n+1}{2}\:if\:n\:is\:odd\end{cases}$$Line independent number (Matching number) = β1 = [n/2] α1 + β1 = n.
Independent Vertex Set
Let ‘G’ = (V, E) be a graph. A subset of ‘V’ is called an independent set of ‘G’ if no two vertices in ‘S’ are adjacent.
Example

Consider the following subsets from the above graphs −
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}Clearly S1 is not an independent vertex set, because for getting an independent vertex set, there should be at least two vertices in the from a graph. But here it is not that case. The subsets S2, S3, and S4 are the independent vertex sets because there is no vertex that is adjacent to any one vertex from the subsets.
Set Vertex Independen Maksimal
Misalkan 'G' adalah sebuah graf, maka himpunan simpul independen dari 'G' dikatakan maksimal jika tidak ada simpul lain dari 'G' yang dapat ditambahkan ke 'S'.
Example
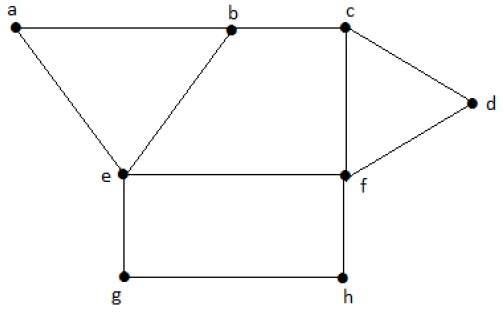
Perhatikan subset berikut dari grafik di atas.
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}S 2 dan S 3 adalah himpunan puncak independen maksimal dari 'G'. Di S 1 dan S 4 , kita bisa menambahkan simpul lain; tetapi di S 2 dan S 3 , kita tidak bisa menambahkan simpul lain.
Set Vertex Independen Maksimum
Himpunan simpul independen maksimal dari 'G' dengan jumlah simpul maksimum disebut sebagai himpunan simpul bebas maksimum.
Example

Pertimbangkan subset berikut dari grafik di atas -
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}Hanya S 3 adalah himpunan puncak independen maksimum, karena mencakup jumlah puncak tertinggi. Jumlah simpul dalam himpunan simpul bebas maksimum 'G' disebut bilangan simpul bebas G (β 2 ).
Example
Untuk grafik lengkap K n ,
Simpul yang menutupi nomor = α 2 = n − 1
Bilangan bebas simpul = β 2 = 1
Anda memiliki α 2 + β 2 = n
Dalam graf lengkap, setiap simpul bersebelahan dengan simpul yang tersisa (n - 1). Oleh karena itu, himpunan independen maksimum K n hanya berisi satu simpul.
Oleh karena itu, β 2 = 1
dan α 2 = | v | - β 2 = n-1
Note - Untuk semua grafik 'G' = (V, E)
- α 2 + β 2 = | v |
- Jika 'S' adalah himpunan puncak independen dari 'G', maka (V - S) adalah penutup puncak dari G.
Pewarnaan graf tidak lain adalah cara sederhana untuk memberi label pada komponen grafik seperti simpul, tepi, dan daerah di bawah beberapa batasan. Dalam grafik, tidak ada dua simpul yang berdekatan, tepi yang berdekatan, atau daerah yang berdekatan yang diwarnai dengan jumlah warna minimum. Nomor ini disebutchromatic number dan grafik tersebut disebut a properly colored graph.
Sedangkan pewarnaan graf, batasan yang ditetapkan pada graf adalah warna, urutan pewarnaan, cara pemberian warna, dll. Pewarnaan diberikan pada suatu simpul atau daerah tertentu. Jadi, simpul atau daerah yang memiliki warna yang sama membentuk himpunan independen.
Pewarnaan Vertex
Pewarnaan simpul adalah pemberian warna pada simpul pada graf 'G' sehingga tidak ada dua simpul yang berdekatan memiliki warna yang sama. Sederhananya, tidak ada dua simpul dari sebuah sisi harus memiliki warna yang sama.
Nomor Chromatic
Jumlah warna minimum yang diperlukan untuk pewarnaan puncak pada graf 'G' disebut bilangan kromatik G, dilambangkan dengan X (G).
χ (G) = 1 jika dan hanya jika 'G' adalah grafik nol. Jika 'G' bukan graf nol, maka χ (G) ≥ 2.
Example
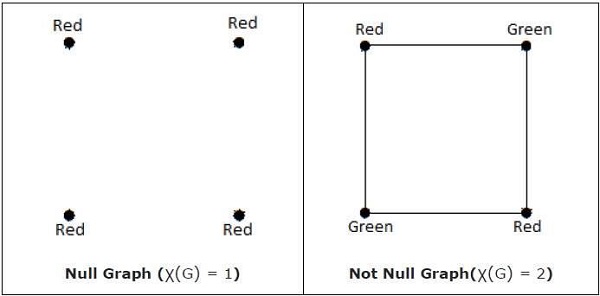
Note - Graf 'G' dikatakan n-coverable jika terdapat pewarnaan simpul yang paling banyak menggunakan n warna, yaitu X (G) ≤ n.
Pewarnaan Wilayah
Pewarnaan wilayah adalah penetapan warna ke wilayah grafik planar sehingga tidak ada dua wilayah yang berdekatan memiliki warna yang sama. Dua daerah dikatakan berdekatan jika mereka memiliki tepi yang sama.
Example
Perhatikan grafik berikut. Wilayah 'aeb' dan 'befc' berdekatan, karena ada tepi yang sama 'menjadi' di antara kedua wilayah tersebut.
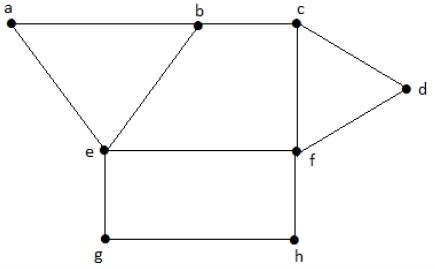
Begitu pula dengan daerah lain yang juga diwarnai berdasarkan kedekatannya. Grafik ini diwarnai sebagai berikut -
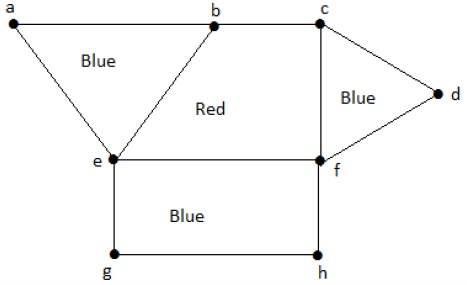
Example
Bilangan kromatik Kn adalah
- n
- n–1
- [n/2]
- [n/2]
Pertimbangkan contoh ini dengan K 4 .

Pada graf lengkap, setiap simpul berbatasan dengan simpul yang tersisa (n - 1). Karenanya, setiap simpul membutuhkan warna baru. Karenanya bilangan kromatik K n = n.
Aplikasi Pewarnaan Grafik
Pewarnaan graf merupakan salah satu konsep terpenting dalam teori graf. Ini digunakan dalam banyak aplikasi ilmu komputer real-time seperti -
- Clustering
- Penambangan data
- Pengambilan gambar
- Segmentasi gambar
- Networking
- Alokasi sumber daya
- Memproses penjadwalan
Sebuah grafik bisa ada dalam berbagai bentuk yang memiliki jumlah simpul, tepi, dan juga konektivitas tepi yang sama. Grafik semacam itu disebut grafik isomorfik. Perhatikan bahwa kami memberi label pada grafik dalam bab ini terutama untuk tujuan merujuk dan mengenalinya satu sama lain.
Grafik Isomorfik
Dua graf G 1 dan G 2 dikatakan isomorfik jika -
Jumlah komponennya (simpul dan tepi) sama.
Konektivitas edge mereka dipertahankan.
Note- Singkatnya, dari dua grafik isomorfik, yang satu adalah versi tweak dari yang lain. Grafik yang tidak berlabel juga dapat dianggap sebagai grafik isomorfik.
There exists a function ‘f’ from vertices of G1 to vertices of G2
[f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.Note
Jika G 1 ≡ G 2 maka -
| V (G 1 ) | = | V (G 2 ) |
| E (G 1 ) | = | E (G 2 ) |
Urutan derajat G 1 dan G 2 sama.
Jika simpul {V 1 , V 2 , .. Vk} membentuk siklus dengan panjang K dalam G 1 , maka simpul {f (V 1 ), f (V 2 ),… f (Vk)} harus membentuk sebuah siklus panjang K di G 2 .
Semua kondisi di atas diperlukan agar grafik G 1 dan G 2 menjadi isomorfik, tetapi tidak cukup untuk membuktikan bahwa grafik tersebut isomorfik.
(G 1 ≡ G 2 ) jika dan hanya jika (G 1 - ≡ G 2 -) dimana G 1 dan G 2 adalah grafik sederhana.
(G 1 ≡ G 2 ) jika matriks ketetanggaan G 1 dan G 2 sama.
(G 1 ≡ G 2 ) jika dan hanya jika subgrafik yang sesuai dari G 1 dan G 2 (diperoleh dengan menghapus beberapa simpul di G1 dan citranya di grafik G 2 ) isomorfik.
Example
Manakah dari grafik berikut yang isomorfik?
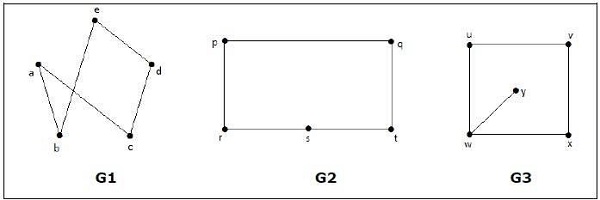
Pada graf G 3 , simpul 'w' hanya berderajat 3, sedangkan semua simpul graf yang lain berderajat 2. Jadi G3 tidak isomorfik terhadap G 1 atau G 2 .
Mengambil pelengkap G 1 dan G 2 , Anda memiliki -
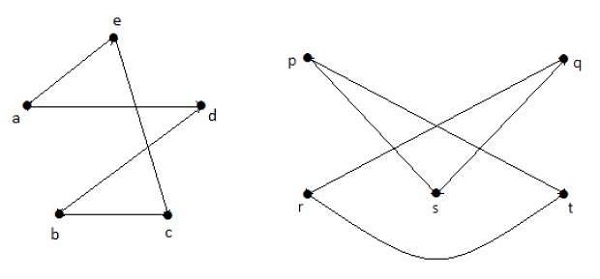
Di sini, (G 1 - ≡ G 2 -), maka (G 1 ≡ G 2 ).
Grafik Planar
Graf 'G' dikatakan planar jika dapat digambar pada bidang atau bola sehingga tidak ada dua sisi yang saling bersilangan pada titik non-simpul.
Example
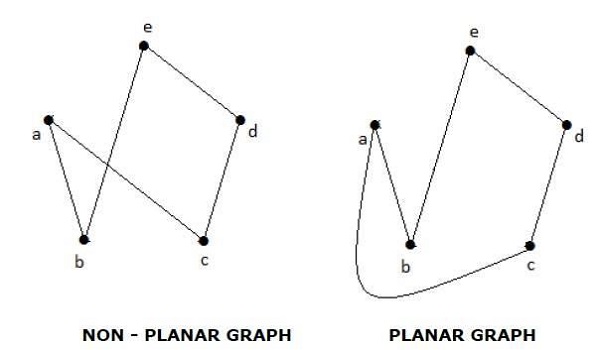
Wilayah
Setiap grafik planar membagi bidang menjadi area terhubung yang disebut region.
Example
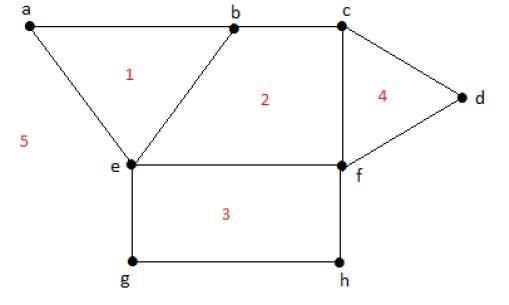
Derajat wilayah yang dibatasi r = deg(r) = Jumlah tepi yang menutupi daerah r.
deg(1) = 3
deg(2) = 4
deg(3) = 4
deg(4) = 3
deg(5) = 8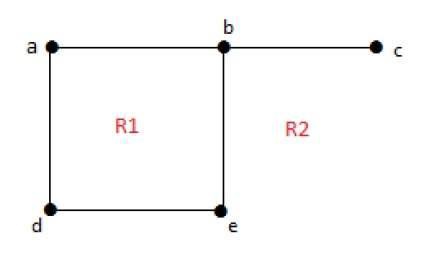
Derajat wilayah tak terbatas r = deg(r) = Jumlah tepi yang menutupi daerah r.
deg(R1) = 4
deg(R2) = 6Dalam grafik planar, properti berikut berlaku -
Dalam grafik planar dengan simpul 'n', jumlah derajat dari semua simpul adalah -
Berdasarkan Sum of Degrees of Regions/ Teorema, dalam grafik planar dengan daerah 'n', Jumlah derajat daerah adalah -
Berdasarkan teorema di atas, Anda dapat menarik kesimpulan berikut -
Dalam grafik planar,
Jika derajat tiap daerah adalah K, maka jumlah derajat daerah adalah -
Jika derajat tiap daerah minimal K (≥ K), maka
Jika derajat tiap daerah paling banyak K (≤ K), maka
Note - Diasumsikan bahwa semua daerah memiliki derajat yang sama.
Berdasarkan Euler’s Formulae pada grafik planar,
Jika graf 'G' adalah planar yang terhubung, maka
Jika grafik planar dengan komponen 'K', maka
Dimana, | V | adalah jumlah simpul, | E | adalah jumlah sisi, dan | R | adalah jumlah wilayah.
Ketimpangan Edge Vertex
Jika 'G' adalah grafik planar yang terhubung dengan derajat setiap daerah minimal 'K' maka,
| E | ≤ k / (k-2) {| v | - 2}
Anda tahu, | V | + | R | = | E | + 2
K. | R | ≤ 2 | E |
K (| E | - | V | + 2) ≤ 2 | E |
(K - 2) | E | ≤ K (| V | - 2)
| E | ≤ k / (k-2) {| v | - 2}
Jika 'G' adalah grafik planar terhubung sederhana, maka
|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4Ada setidaknya satu simpul V • ∈ G, sehingga derajat (V) ≤ 5.
Jika 'G' adalah grafik planar terhubung sederhana (dengan setidaknya 2 sisi) dan tanpa segitiga, maka
|E| ≤ {2|V| – 4}Teorema Kuratowski
Grafik 'G' adalah non-planar jika dan hanya jika 'G' memiliki subgraf yang bersifat homeomorfik terhadap K 5 atau K 3,3 .
Homomorfisme
Dua graf G 1 dan G 2 dikatakan homomorfik, jika masing-masing graf tersebut dapat diperoleh dari graf yang sama 'G' dengan membagi beberapa sisi G dengan lebih banyak simpul. Lihat contoh berikut -

Bagilah tepi 'rs' menjadi dua sisi dengan menambahkan satu simpul.
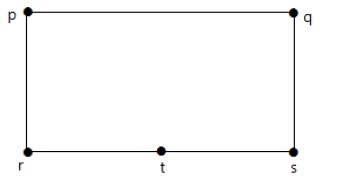
Grafik yang ditunjukkan di bawah ini homomorfik dengan grafik pertama.
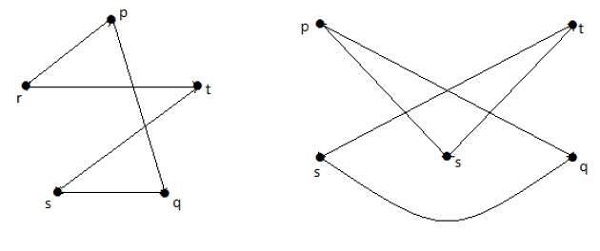
Jika G 1 isomorfik terhadap G 2 , maka G bersifat homeomorfik bagi G2 tetapi kebalikannya tidak harus benar.
Grafik apa pun dengan 4 simpul atau kurang adalah planar.
Grafik apa pun dengan 8 tepi atau kurang adalah planar.
Grafik lengkap K n adalah planar jika dan hanya jika n ≤ 4.
Graf bipartit lengkap K m, n adalah planar jika dan hanya jika m ≤ 2 atau n ≤ 2.
Grafik non-planar sederhana dengan jumlah simpul minimum adalah graf lengkap K 5 .
Grafik non-planar sederhana dengan jumlah sisi minimum adalah K 3, 3 .
Grafik polihedral
Graf planar terhubung sederhana disebut graf polihedral jika derajat tiap simpul ≥ 3, yaitu derajat (V) ≥ 3 ∀ V ∈ G.
3 | V | ≤ 2 | E |
3 | R | ≤ 2 | E |
Grafik dapat dilalui jika Anda dapat menggambar jalur di antara semua simpul tanpa menelusuri kembali jalur yang sama. Berdasarkan jalur ini, ada beberapa kategori seperti jalur Euler dan sirkuit Euler yang dijelaskan dalam bab ini.
Jalan Euler
Lintasan Euler berisi setiap tepi 'G' tepat satu kali dan setiap simpul 'G' setidaknya sekali. Grafik terhubung G dikatakan dapat dilalui jika mengandung jalur Euler.
Example
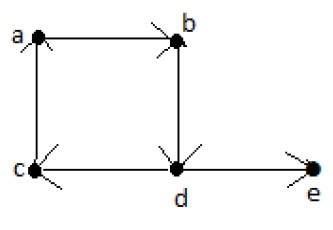
Jalan Euler = dcabde.
Sirkuit Euler
Dalam lintasan Euler, jika simpul awal sama dengan simpul akhir, maka itu disebut rangkaian Euler.
Example
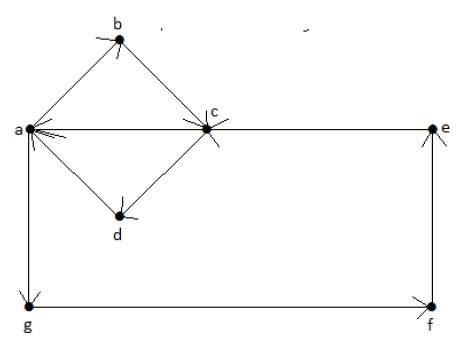
Euler’s Path = abcdagfeca.
Teorema Sirkuit Euler
Sebuah graf terhubung 'G' dapat dilintasi jika dan hanya jika jumlah simpul dengan derajat ganjil di G tepat 2 atau 0. Sebuah graf terhubung G dapat berisi lintasan Euler, tetapi bukan rangkaian Euler, jika ia memiliki tepat dua simpul dengan derajat yang aneh.
Note - Jalur Euler ini dimulai dengan simpul berderajat ganjil dan diakhiri dengan simpul berderajat ganjil lainnya.
Example
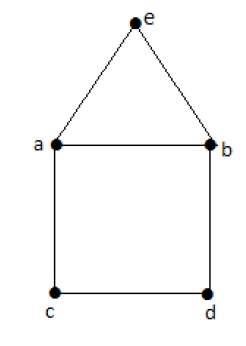
Euler’s Path- beabdca bukanlah sirkuit Euler, tetapi jalur Euler. Jelas itu memiliki tepat 2 simpul derajat ganjil.
Note - Pada graf terhubung G, jika banyaknya simpul dengan derajat ganjil = 0, maka rangkaian Euler ada.
Grafik Hamiltonian
Graf terhubung G dikatakan graf Hamilton, jika terdapat siklus yang memuat semua simpul G.
Setiap siklus adalah rangkaian tetapi rangkaian dapat berisi banyak siklus. Siklus seperti itu disebut aHamiltonian cycle dari G.
Jalan Hamilton
Sebuah graf terhubung dikatakan Hamiltonian jika graf tersebut mengandung setiap simpul G tepat satu kali. Jalan seperti itu disebut aHamiltonian path.
Example
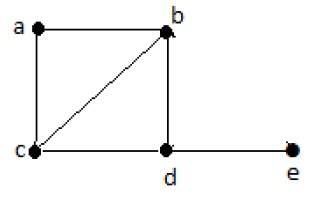
Hamiltonian Path- edbac.
Note
Sirkuit Euler berisi setiap tepi grafik tepat satu kali.
Dalam siklus Hamiltonian, beberapa tepi grafik dapat dilewati.
Example
Perhatikan grafik berikut -
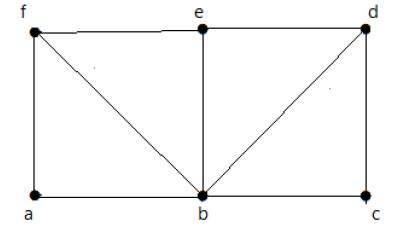
Untuk grafik yang ditunjukkan di atas -
Jalur Euler ada - salah
Sirkuit Euler ada - salah
Siklus Hamiltonian ada - benar
Jalan Hamiltonian ada - benar
G memiliki empat simpul dengan derajat ganjil, sehingga tidak dapat dilalui. Dengan melewatkan tepi internal, grafik memiliki siklus Hamiltonian yang melewati semua simpul.
Dalam bab ini, kita akan membahas beberapa contoh standar untuk mendemonstrasikan konsep yang telah kita bahas di bab sebelumnya.
Contoh 1
Find the number of spanning trees in the following graph.
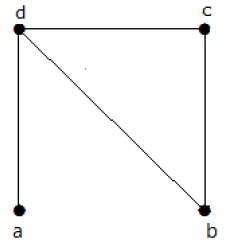
Larutan
Jumlah pohon merentang yang diperoleh dari grafik di atas adalah 3. Mereka adalah sebagai berikut -
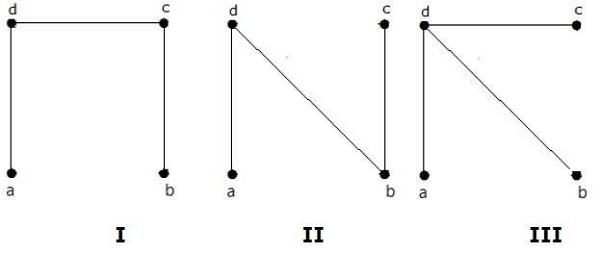
Ketiganya adalah pohon rentang untuk grafik yang diberikan. Di sini grafik I dan II bersifat isomorfik satu sama lain. Jelasnya, jumlah pohon rentang non-isomorfik adalah dua.
Contoh 2
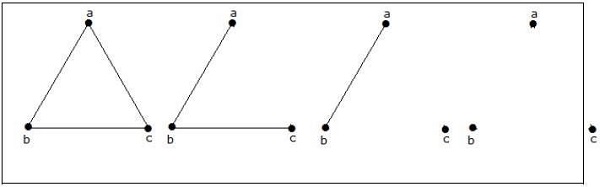
How many simple non-isomorphic graphs are possible with 3 vertices?
Larutan
Ada 4 grafik non-isomorfik yang dimungkinkan dengan 3 simpul. Mereka ditunjukkan di bawah ini.
Contoh 3
Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.
Larutan
Dengan jumlah teorema derajat,
20 Σ i = 1 derajat (Vi) = 2 | E |
20 (3) = 2 | E |
| E | = 30
Dengan rumus Euler,
| V | + | R | = | E | + 2
20+ | R | = 30 + 2
| R | = 12
Sehingga jumlah wilayahnya ada 12.
Contoh 4
What is the chromatic number of complete graph Kn?
Larutan
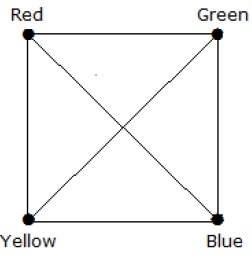
Dalam graf lengkap, setiap simpul bersebelahan dengan simpul yang tersisa (n – 1). Karenanya, setiap simpul membutuhkan warna baru. Karenanya bilangan kromatik K n = n.
Contoh 5
What is the matching number for the following graph?
Larutan
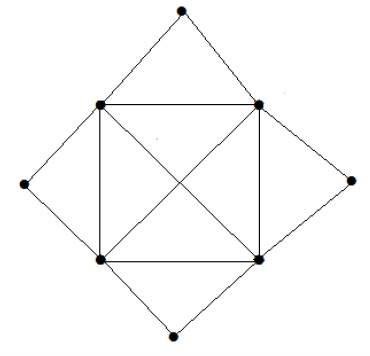
Jumlah simpul = 9
Kita hanya bisa mencocokkan 8 simpul.
Nomor yang cocok adalah 4.
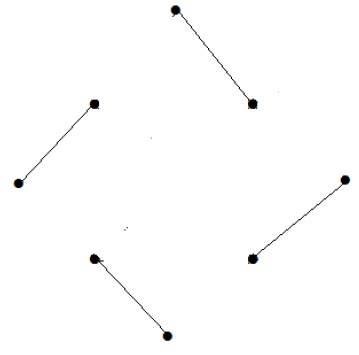
Contoh 6
What is the line covering number of for the following graph?
Larutan
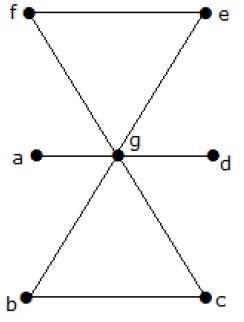
Jumlah simpul = | V | = n = 7
Nomor penutup garis = (α 1 ) ≥ [n / 2] = 3
α 1 ≥ 3
Dengan menggunakan 3 sisi, kita bisa menutupi semua simpul.
Oleh karena itu, nomor penutup garis adalah 3.