Teori Grafik - Pencocokan
Grafik yang cocok adalah subgraf dari grafik yang tidak memiliki tepi yang berdekatan satu sama lain. Sederhananya, seharusnya tidak ada simpul yang sama di antara dua sisi mana pun.
Sesuai
Misalkan 'G' = (V, E) menjadi grafik. Sebuah subgraf disebut pencocokan M (G),if each vertex of G is incident with at most one edge in M, yaitu,
derajat (V) ≤ 1 ∀ V ∈ G
yang berarti dalam pencocokan graf M (G), simpul harus memiliki derajat 1 atau 0, di mana tepi harus bersisian dengan graf G.
Notation - M (G)
Example
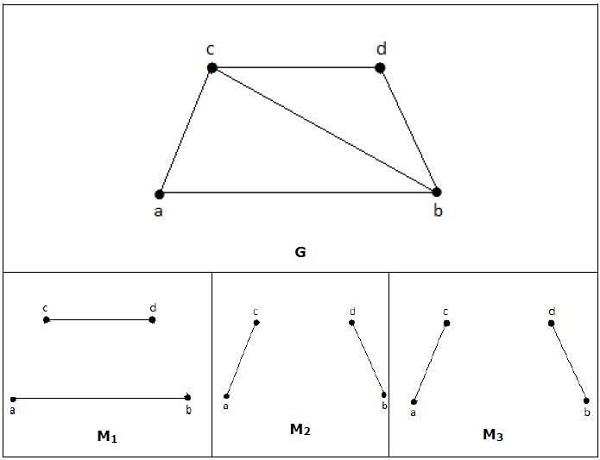

Dalam pencocokan,
jika derajat (V) = 1, maka (V) dikatakan cocok
jika derajat (V) = 0, maka (V) tidak cocok.
Dalam pencocokan, tidak ada dua sisi yang berdekatan. Karena jika ada dua sisi yang berdekatan, maka derajat dari titik sudut yang menghubungkan kedua sisi tersebut akan memiliki derajat 2 yang melanggar aturan pencocokan.
Pencocokan Maksimal
M yang cocok dari grafik 'G' dikatakan maksimal if no other edges of ‘G’ can be added to M.
Example

M1, M2, M3 dari grafik di atas adalah pencocokan maksimal G.
Pencocokan Maksimum
Ini juga dikenal sebagai pencocokan maksimal terbesar. Pencocokan maksimum didefinisikan sebagai pencocokan maksimal dengan jumlah tepi maksimum.
Jumlah tepi dalam pencocokan maksimum 'G' disebut nya matching number.
Example
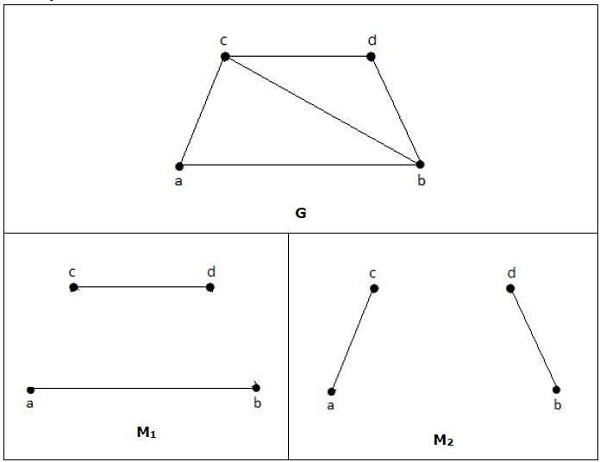
Untuk graf yang diberikan pada contoh di atas, M1 dan M2 adalah kecocokan maksimum dari 'G' dan angka kecocokannya adalah 2. Oleh karena itu dengan menggunakan graf G, kita hanya dapat membentuk subgrafik dengan maksimal hanya 2 sisi. Karenanya kami memiliki nomor yang cocok sebagai dua.
Pencocokan Sempurna
Pencocokan (M) pada graf (G) dikatakan sama sempurna, jika setiap simpul pada graf g (G) bersisian dengan tepat satu tepi yang cocok (M), yaitu,
derajat (V) = 1 ∀ V
Derajat setiap simpul di subgraf harus memiliki derajat 1.
Example
Pada grafik berikut, M1 dan M2 adalah contoh pencocokan sempurna dari G.
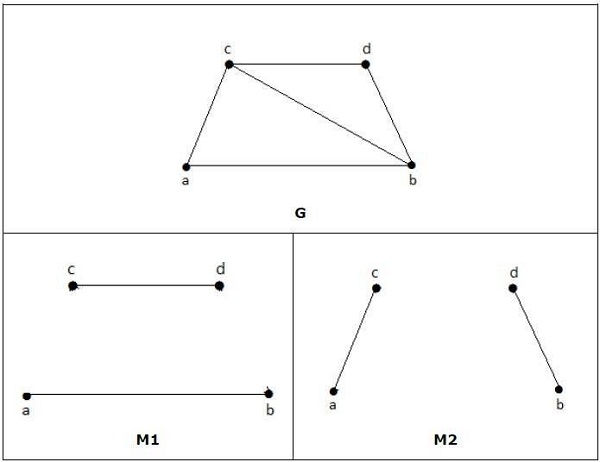
Note - Setiap pencocokan sempurna dari grafik juga merupakan pencocokan maksimum grafik, karena tidak ada peluang untuk menambahkan satu tepi lagi dalam grafik yang cocok sempurna.
Pencocokan grafik yang maksimal tidak harus sempurna. Jika graf 'G' memiliki kecocokan sempurna, maka jumlah simpul | V (G) | genap. Jika ganjil, maka simpul terakhir berpasangan dengan simpul lainnya, dan akhirnya tersisa satu simpul tunggal yang tidak dapat dipasangkan dengan simpul lain yang derajatnya nol. Ini jelas melanggar prinsip pencocokan sempurna.
Example
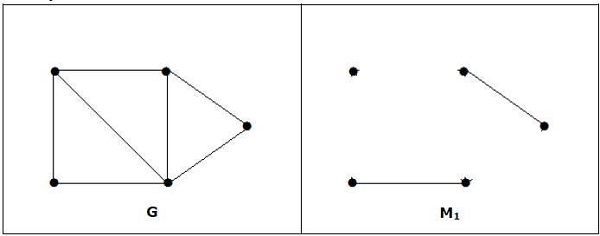
Note- Kebalikan dari pernyataan di atas tidak harus benar. Jika G memiliki jumlah simpul genap, maka M1 tidak perlu sempurna.
Example
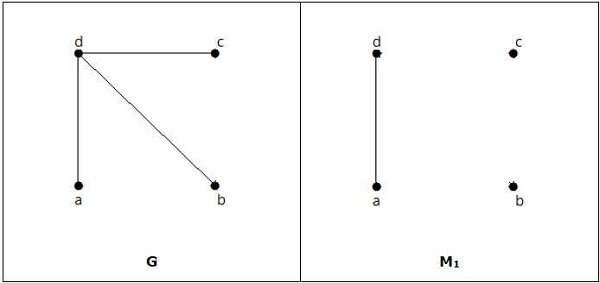
Ini cocok, tetapi bukan pasangan yang sempurna, meskipun jumlah simpulnya genap.