MATLAB - Operator

Operator adalah simbol yang memberi tahu kompiler untuk melakukan manipulasi matematika atau logika tertentu. MATLAB dirancang untuk beroperasi terutama pada seluruh matriks dan array. Oleh karena itu, operator di MATLAB bekerja pada data skalar dan non-skalar. MATLAB memungkinkan jenis operasi dasar berikut -

Operator Aritmatika
Operator Relasional
Operator Logis
Operasi Bitwise
Atur Operasi

Operator Aritmatika

MATLAB memungkinkan dua jenis operasi aritmatika -

Operasi aritmatika matriks
Operasi aritmatika array

Operasi aritmatika matriks sama seperti yang didefinisikan dalam aljabar linier. Operasi array dijalankan elemen demi elemen, baik pada array satu dimensi maupun multidimensi.

Operator matriks dan operator array dibedakan oleh simbol titik (.). Namun, karena operasi penjumlahan dan pengurangan sama untuk matriks dan array, operatornya sama untuk kedua kasus. Tabel berikut memberikan penjelasan singkat tentang operator -

Tunjukkan Contoh

Sr.No.	Operator & Deskripsi
1	+ Penambahan atau plus unary. A + B menambahkan nilai yang disimpan dalam variabel A dan B. A dan B harus memiliki ukuran yang sama, kecuali salah satunya adalah skalar. Skalar dapat ditambahkan ke matriks dengan ukuran berapa pun.
2	- Pengurangan atau minus unary. AB mengurangi nilai B dari A. A dan B harus memiliki ukuran yang sama, kecuali salah satunya adalah skalar. Skalar dapat dikurangi dari matriks dengan ukuran berapa pun.
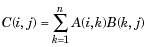
3	* Perkalian matriks. C = A * B adalah produk aljabar linier dari matriks A dan B. Lebih tepatnya, Untuk non-skalar A dan B, jumlah kolom A harus sama dengan jumlah baris B. Skalar dapat mengalikan matriks dengan ukuran berapa pun.
4	.* Perkalian array. A. * B adalah produk elemen demi elemen dari array A dan B. A dan B harus memiliki ukuran yang sama, kecuali salah satunya adalah skalar.
5	/ Pembagian kanan garis miring atau matriks. B / A kira-kira sama dengan B * inv (A). Lebih tepatnya, B / A = (A '\ B') '.
6	./ Pembagian kanan array. A./B adalah matriks dengan elemen A (i, j) / B (i, j). A dan B harus memiliki ukuran yang sama, kecuali salah satunya adalah skalar.
7	\ Garis miring terbalik atau pembagian kiri matriks. Jika A adalah matriks persegi, A \ B kira-kira sama dengan inv (A) * B, kecuali jika dihitung dengan cara yang berbeda. Jika A adalah n-by-n matriks dan B adalah vektor kolom dengan komponen n, atau matriks dengan beberapa kolom tersebut, maka X = A \ B adalah solusi untuk persamaan AX = B . Pesan peringatan ditampilkan jika skala A buruk atau hampir tunggal.
8	.\ Divisi kiri array. A. \ B adalah matriks dengan elemen B (i, j) / A (i, j). A dan B harus memiliki ukuran yang sama, kecuali salah satunya adalah skalar.
9	^ Kekuatan matriks. X ^ p adalah X pangkat p, jika p adalah skalar. Jika p adalah bilangan bulat, daya dihitung dengan kuadrat berulang. Jika bilangan bulatnya negatif, X dibalik terlebih dahulu. Untuk nilai p lainnya, perhitungannya melibatkan nilai eigen dan vektor eigen, sehingga jika [V, D] = eig (X), maka X ^ p = V * D. ^ p / V.
10	.^ Kekuatan array. A. ^ B adalah matriks dengan elemen A (i, j) pangkat B (i, j). A dan B harus memiliki ukuran yang sama, kecuali salah satunya adalah skalar.
11	' Transpos matriks. A 'adalah transposisi aljabar linier dari A. Untuk matriks kompleks, ini adalah transpos konjugat kompleks.
12	.' Transpose array. SEBUAH.' adalah transpos array dari A. Untuk matriks kompleks, ini tidak melibatkan konjugasi.

Operator Relasional

Operator relasional juga dapat bekerja pada data skalar dan non-skalar. Operator relasional untuk array melakukan perbandingan elemen-demi-elemen antara dua array dan mengembalikan array logis dengan ukuran yang sama, dengan elemen yang disetel ke logika 1 (benar) di mana relasinya benar dan elemen disetel ke logika 0 (salah) di mana itu berada tidak.

Tabel berikut menunjukkan operator relasional yang tersedia di MATLAB -

Tunjukkan Contoh

Sr.No.	Operator & Deskripsi
1	< Kurang dari
2	<= Kurang dari atau sama dengan
3	> Lebih besar dari
4	>= Lebih dari atau sama dengan
5	== Sama dengan
6	~= Tidak sebanding dengan

Operator Logis

MATLAB menawarkan dua jenis operator dan fungsi logika -

Elemen-bijaksana - Operator ini beroperasi pada elemen yang sesuai dari array logis.
Hubungan pendek - Operator ini beroperasi pada skalar dan, ekspresi logis.

Operator logika berdasarkan elemen mengoperasikan elemen demi elemen pada array logis. Simbol &, |, dan ~ adalah operator larik logika AND, OR, dan NOT.

Operator logika sirkuit pendek memungkinkan hubungan pendek pada operasi logis. Simbol && dan || adalah operator hubung singkat logis AND dan OR.

Tunjukkan Contoh

Operasi Bitwise

Operator bitwise bekerja pada bit dan melakukan operasi bit demi bit. Tabel kebenaran untuk &, |, dan ^ adalah sebagai berikut -

p	q	p & q	p \| q	p ^ q
0	0	0	0	0
0	1	0	1	1
1	1	1	1	0
1	0	0	1	1

Asumsikan jika A = 60; dan B = 13; Sekarang dalam format biner akan menjadi sebagai berikut -

A = 0011 1100

B = 0000 1101

-----------------

A&B = 0000 1100

A | B = 0011 1101

A ^ B = 0011 0001

~ A = 1100 0011

MATLAB menyediakan berbagai fungsi untuk operasi bit-bijaksana seperti operasi 'bitwise dan', 'bitwise atau' dan 'bitwise not', operasi shift, dll.

Tabel berikut menunjukkan operasi bitwise yang umum digunakan -

Tunjukkan Contoh

Fungsi	Tujuan
bitand (a, b)	Sedikit demi sedikit AND dari bilangan bulat a dan b
bitcmp (a)	Pelengkap yang bijak dari a
bitget (a, pos)	Mendapatkan sedikit pada posisi yang ditentukan pos , dalam array integer a
bitor (a, b)	Bit-bijaksana OR dari bilangan bulat a dan b
bitset (a, pos)	Set bit pada lokasi tertentu pos dari sebuah
bitshift (a, k)	Mengembalikan a yang digeser ke kiri dengan k bit, setara dengan mengalikan dengan 2 ^k . Nilai negatif k sesuai dengan menggeser bit ke kanan atau membagi dengan 2 ^{\| k \|}dan pembulatan ke bilangan bulat terdekat menuju tak terbatas negatif. Setiap bit luapan terpotong.
bitxor (a, b)	XOR bit-bit dari bilangan bulat a dan b
swapbytes	Tukar urutan byte

Atur Operasi

MATLAB menyediakan berbagai fungsi untuk operasi set, seperti penyatuan, persimpangan dan pengujian untuk keanggotaan set, dll.

Tabel berikut menunjukkan beberapa operasi set yang umum digunakan -

Tunjukkan Contoh

Sr.No.	Deskripsi fungsi
1	intersect(A,B) Set persimpangan dua larik; mengembalikan nilai yang sama untuk A dan B. Nilai yang dikembalikan berada dalam urutan yang diurutkan.
2	intersect(A,B,'rows') Memperlakukan setiap baris A dan setiap baris B sebagai entitas tunggal dan mengembalikan baris yang sama untuk A dan B. Baris dari matriks yang dikembalikan berada dalam urutan yang diurutkan.
3	ismember(A,B) Mengembalikan larik berukuran sama dengan A, berisi 1 (benar) di mana elemen A ditemukan di B. Di tempat lain, mengembalikan 0 (salah).
4	ismember(A,B,'rows') Memperlakukan setiap baris A dan setiap baris B sebagai entitas tunggal dan mengembalikan vektor yang berisi 1 (benar) di mana baris matriks A juga baris B. Di tempat lain, ia mengembalikan 0 (salah).
5	issorted(A) Mengembalikan logika 1 (benar) jika elemen A dalam urutan yang diurutkan dan logika 0 (salah) sebaliknya. Input A bisa berupa vektor atau larik sel string N-by-1 atau 1-by-N.A is considered to be sorted if A dan keluaran dari sort (A) adalah sama.
6	issorted(A, 'rows') Mengembalikan logika 1 (benar) jika baris dari matriks dua dimensi A dalam urutan yang diurutkan, dan logika 0 (salah) sebaliknya. Matrix A is considered to be sorted if A dan keluaran dari pengurutan (A) sama.
7	setdiff(A,B) Menetapkan perbedaan dua larik; mengembalikan nilai di A yang tidak ada di B. Nilai dalam larik yang dikembalikan berada dalam urutan yang diurutkan.
8	setdiff(A,B,'rows') Memperlakukan setiap baris A dan setiap baris B sebagai entitas tunggal dan mengembalikan baris dari A yang tidak ada di B. Baris dari matriks yang dikembalikan berada dalam urutan yang diurutkan. Opsi 'baris' tidak mendukung larik sel.
9	setxor Menetapkan OR eksklusif dari dua larik
10	union Menetapkan gabungan dua larik
11	unique Nilai unik dalam array