MATLAB - Panduan Cepat
MATLAB (laboratorium matriks) adalah bahasa pemrograman tingkat tinggi generasi keempat dan lingkungan interaktif untuk komputasi numerik, visualisasi, dan pemrograman.
MATLAB dikembangkan oleh MathWorks.
Ini memungkinkan manipulasi matriks; merencanakan fungsi dan data; implementasi algoritma; pembuatan antarmuka pengguna; berinteraksi dengan program yang ditulis dalam bahasa lain, termasuk C, C ++, Java, dan FORTRAN; menganalisis data; mengembangkan algoritma; dan membuat model dan aplikasi.
Ini memiliki banyak perintah bawaan dan fungsi matematika yang membantu Anda dalam perhitungan matematika, menghasilkan plot, dan melakukan metode numerik.
Kekuatan Matematika Komputasi MATLAB
MATLAB digunakan dalam setiap aspek matematika komputasi. Berikut adalah beberapa perhitungan matematis yang umum digunakan yang paling sering digunakan -
- Berurusan dengan Matriks dan Array
- 2-D dan 3-D Plotting dan grafik
- Aljabar linier
- Persamaan Aljabar
- Fungsi Non-linier
- Statistics
- Analisis data
- Kalkulus dan Persamaan Diferensial
- Perhitungan Numerik
- Integration
- Transforms
- Pemasangan Kurva
- Berbagai fungsi khusus lainnya
Fitur MATLAB
Berikut adalah fitur dasar MATLAB -
Ini adalah bahasa tingkat tinggi untuk komputasi numerik, visualisasi, dan pengembangan aplikasi.
Ini juga menyediakan lingkungan interaktif untuk eksplorasi berulang, desain dan pemecahan masalah.
Ini menyediakan perpustakaan yang luas dari fungsi matematika untuk aljabar linier, statistik, analisis Fourier, pemfilteran, pengoptimalan, integrasi numerik dan penyelesaian persamaan diferensial biasa.
Ini menyediakan grafik built-in untuk memvisualisasikan data dan alat untuk membuat plot kustom.
Antarmuka pemrograman MATLAB memberikan alat pengembangan untuk meningkatkan pemeliharaan kualitas kode dan memaksimalkan kinerja.
Ini menyediakan alat untuk membangun aplikasi dengan antarmuka grafis khusus.
Ini menyediakan fungsi untuk mengintegrasikan algoritma berbasis MATLAB dengan aplikasi eksternal dan bahasa seperti C, Java, .NET dan Microsoft Excel.
Kegunaan MATLAB
MATLAB banyak digunakan sebagai alat komputasi dalam sains dan teknik yang mencakup bidang fisika, kimia, matematika, dan semua aliran teknik. Ini digunakan dalam berbagai aplikasi termasuk -
- Pemrosesan Sinyal dan Komunikasi
- Pemrosesan Gambar dan Video
- Sistem kontrol
- Tes dan Pengukuran
- Keuangan Komputasi
- Biologi Komputasi
Pengaturan Lingkungan Lokal
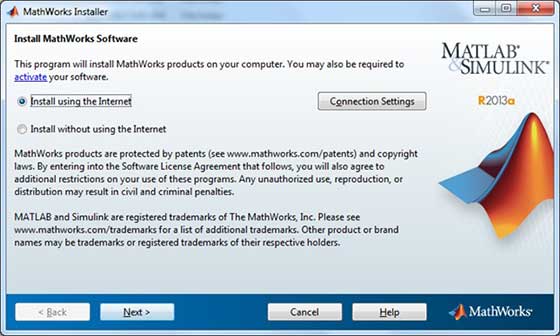
Menyiapkan lingkungan MATLAB hanya dengan beberapa klik. Penginstal dapat diunduh dari sini .
MathWorks menyediakan produk berlisensi, versi uji coba, dan versi siswa juga. Anda perlu masuk ke situs dan menunggu sedikit untuk persetujuan mereka.
Setelah mengunduh penginstal, perangkat lunak dapat diinstal melalui beberapa klik.
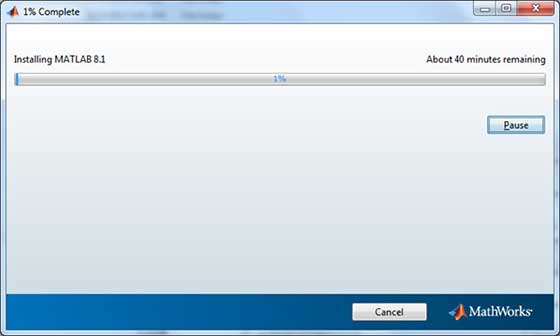
Memahami Lingkungan MATLAB
IDE pengembangan MATLAB dapat diluncurkan dari ikon yang dibuat di desktop. Jendela kerja utama di MATLAB disebut desktop. Saat MATLAB dimulai, desktop muncul dalam tata letak default -
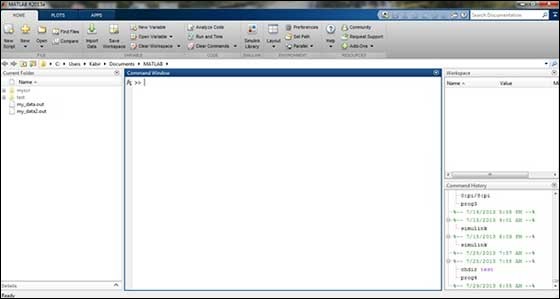
Desktop memiliki panel berikut -
Current Folder - Panel ini memungkinkan Anda mengakses folder dan file proyek.
Command Window- Ini adalah area utama di mana perintah dapat dimasukkan pada baris perintah. Ini ditunjukkan oleh prompt perintah (>>).
Workspace - Ruang kerja menampilkan semua variabel yang dibuat dan / atau diimpor dari file.
Command History - Panel ini menampilkan atau mengembalikan perintah yang dimasukkan pada baris perintah.


Siapkan GNU Octave
Jika Anda ingin menggunakan Octave di mesin Anda (Linux, BSD, OS X atau Windows), silakan unduh versi terbaru dari Download GNU Octave . Anda dapat memeriksa instruksi instalasi yang diberikan untuk mesin Anda.
Lingkungan MATLAB berperilaku seperti kalkulator super kompleks. Anda dapat memasukkan perintah di >> command prompt.
MATLAB adalah lingkungan yang ditafsirkan. Dengan kata lain, Anda memberikan perintah dan MATLAB langsung menjalankannya.
Praktik Langsung
Ketikkan ekspresi yang valid, misalnya,
5 + 5Dan tekan ENTER
Ketika Anda mengklik tombol Execute, atau mengetik Ctrl + E, MATLAB segera menjalankannya dan hasil yang dikembalikan adalah -
ans = 10Mari kita ambil beberapa contoh lagi -
3 ^ 2 % 3 raised to the power of 2Ketika Anda mengklik tombol Execute, atau mengetik Ctrl + E, MATLAB segera menjalankannya dan hasil yang dikembalikan adalah -
ans = 9Contoh lain,
sin(pi /2) % sine of angle 90oKetika Anda mengklik tombol Execute, atau mengetik Ctrl + E, MATLAB segera menjalankannya dan hasil yang dikembalikan adalah -
ans = 1Contoh lain,
7/0 % Divide by zeroKetika Anda mengklik tombol Execute, atau mengetik Ctrl + E, MATLAB segera menjalankannya dan hasil yang dikembalikan adalah -
ans = Inf
warning: division by zeroContoh lain,
732 * 20.3Ketika Anda mengklik tombol Execute, atau mengetik Ctrl + E, MATLAB segera menjalankannya dan hasil yang dikembalikan adalah -
ans = 1.4860e+04MATLAB menyediakan beberapa ekspresi khusus untuk beberapa simbol matematika, seperti pi untuk π, Inf untuk ∞, i (dan j) untuk √-1 dll. Nan singkatan dari 'bukan angka'.
Penggunaan Titik Koma (;) di MATLAB
Titik koma (;) menunjukkan akhir pernyataan. Namun, jika Anda ingin menyembunyikan dan menyembunyikan output MATLAB untuk ekspresi, tambahkan titik koma setelah ekspresi.
Sebagai contoh,
x = 3;
y = x + 5Ketika Anda mengklik tombol Execute, atau mengetik Ctrl + E, MATLAB segera menjalankannya dan hasil yang dikembalikan adalah -
y = 8Menambahkan Komentar
Simbol persen (%) digunakan untuk menunjukkan baris komentar. Sebagai contoh,
x = 9 % assign the value 9 to xAnda juga dapat menulis blok komentar menggunakan operator blokir komentar% {dan%}.
Editor MATLAB menyertakan alat dan item menu konteks untuk membantu Anda menambah, menghapus, atau mengubah format komentar.
Operator yang umum digunakan dan Karakter Khusus
MATLAB mendukung operator yang umum digunakan dan karakter khusus berikut -
| Operator | Tujuan |
|---|---|
| + | Plus; operator tambahan. |
| - | Minus; operator pengurangan. |
| * | Operator perkalian skalar dan matriks. |
| .* | Operator perkalian array. |
| ^ | Operator eksponensial skalar dan matriks. |
| .^ | Operator eksponen array. |
| \ | Operator divisi kiri. |
| / | Operator divisi kanan. |
| .\ | Larik operator divisi kiri. |
| ./ | Larik operator divisi kanan. |
| : | Usus besar; menghasilkan elemen dengan jarak teratur dan mewakili seluruh baris atau kolom. |
| ( ) | Tanda kurung; menyertakan argumen fungsi dan indeks larik; mengesampingkan prioritas. |
| [ ] | Tanda kurung; mengurung elemen array. |
| . | Titik desimal. |
| … | Elipsis; operator kelanjutan jalur |
| , | Koma; memisahkan pernyataan dan elemen dalam satu baris |
| ; | Titik koma; memisahkan kolom dan menyembunyikan tampilan. |
| % | Tanda persen; menunjuk komentar dan menentukan pemformatan. |
| _ | Tanda kutip dan operator transpos. |
| ._ | Operator transpos tidak terkonjugasi. |
| = | Operator penugasan. |
Variabel dan Konstanta Khusus
MATLAB mendukung variabel dan konstanta khusus berikut -
| Nama | Berarti |
|---|---|
| ans | Jawaban terbaru. |
| eps | Akurasi presisi floating-point. |
| i,j | Satuan imajiner √-1. |
| Inf | Infinity. |
| NaN | Hasil numerik tidak ditentukan (bukan angka). |
| pi | Angka π |
Variabel Penamaan
Nama variabel terdiri dari huruf yang diikuti dengan sejumlah huruf, angka, atau garis bawah.
MATLAB adalah case-sensitive.
Nama variabel bisa berapa pun panjangnya, namun MATLAB hanya menggunakan karakter N pertama, di mana N diberikan oleh fungsinya namelengthmax.
Menyimpan Pekerjaan Anda
Itu save perintah digunakan untuk menyimpan semua variabel di ruang kerja, sebagai file dengan ekstensi .mat, di direktori saat ini.
Sebagai contoh,
save myfileAnda dapat memuat ulang file kapan saja nanti menggunakan load perintah.
load myfileDalam lingkungan MATLAB, setiap variabel adalah array atau matriks.
Anda dapat menetapkan variabel dengan cara yang sederhana. Sebagai contoh,
x = 3 % defining x and initializing it with a valueMATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
x = 3Ini membuat matriks 1-oleh-1 bernama x dan menyimpan nilai 3 dalam elemennya. Mari kita periksa contoh lainnya,
x = sqrt(16) % defining x and initializing it with an expressionMATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
x = 4Harap dicatat bahwa -
Setelah variabel dimasukkan ke dalam sistem, Anda dapat merujuknya nanti.
Variabel harus memiliki nilai sebelum digunakan.
Ketika ekspresi mengembalikan hasil yang tidak ditetapkan ke variabel apa pun, sistem menetapkannya ke variabel bernama ans, yang dapat digunakan nanti.
Sebagai contoh,
sqrt(78)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans = 8.8318Anda dapat menggunakan variabel ini ans -
sqrt(78);
9876/ansMATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans = 1118.2Mari kita lihat contoh lain -
x = 7 * 8;
y = x * 7.89MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
y = 441.84Tugas Ganda
Anda dapat memiliki banyak tugas di baris yang sama. Sebagai contoh,
a = 2; b = 7; c = a * bMATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
c = 14Saya telah melupakan Variabel!
Itu who perintah menampilkan semua nama variabel yang telah Anda gunakan.
whoMATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
Your variables are:
a ans b cItu whos perintah menampilkan lebih banyak tentang variabel -
- Variabel saat ini dalam memori
- Jenis setiap variabel
- Memori dialokasikan untuk setiap variabel
- Apakah itu variabel kompleks atau bukan
whosMATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
Attr Name Size Bytes Class
==== ==== ==== ==== =====
a 1x1 8 double
ans 1x70 757 cell
b 1x1 8 double
c 1x1 8 double
Total is 73 elements using 781 bytesItu clear perintah menghapus semua (atau variabel tertentu) dari memori.
clear x % it will delete x, won't display anything
clear % it will delete all variables in the workspace
% peacefully and unobtrusivelyTugas Panjang
Penugasan yang panjang dapat diperpanjang ke baris lain dengan menggunakan elipsis (...). Sebagai contoh,
initial_velocity = 0;
acceleration = 9.8;
time = 20;
final_velocity = initial_velocity + acceleration * timeMATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
final_velocity = 196Perintah format
Secara default, MATLAB menampilkan angka dengan empat nilai tempat desimal. Ini dikenal sebagaishort format.
Namun, jika Anda ingin lebih presisi, Anda perlu menggunakan file format perintah.
Itu format long Perintah menampilkan 16 digit setelah desimal.
Misalnya -
format long
x = 7 + 10/3 + 5 ^ 1.2MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil berikut-
x = 17.2319816406394Contoh lain,
format short
x = 7 + 10/3 + 5 ^ 1.2MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
x = 17.232Itu format bankperintah membulatkan angka ke dua tempat desimal. Sebagai contoh,
format bank
daily_wage = 177.45;
weekly_wage = daily_wage * 6MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
weekly_wage = 1064.70MATLAB menampilkan angka besar menggunakan notasi eksponensial.
Itu format short e perintah memungkinkan menampilkan dalam bentuk eksponensial dengan empat tempat desimal ditambah eksponen.
Sebagai contoh,
format short e
4.678 * 4.9MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans = 2.2922e+01Itu format long eperintah memungkinkan menampilkan dalam bentuk eksponensial dengan empat tempat desimal ditambah eksponen. Sebagai contoh,
format long e
x = piMATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
x = 3.141592653589793e+00Itu format ratperintah memberikan ekspresi rasional terdekat yang dihasilkan dari perhitungan. Sebagai contoh,
format rat
4.678 * 4.9MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans = 34177/1491Membuat Vektor
Vektor adalah deretan angka satu dimensi. MATLAB memungkinkan pembuatan dua jenis vektor -
- Vektor baris
- Vektor kolom
Row vectors dibuat dengan mengapit kumpulan elemen dalam tanda kurung siku, menggunakan spasi atau koma untuk membatasi elemen.
Sebagai contoh,
r = [7 8 9 10 11]MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
r =
7 8 9 10 11Contoh lain,
r = [7 8 9 10 11];
t = [2, 3, 4, 5, 6];
res = r + tMATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
res =
9 11 13 15 17Column vectors dibuat dengan mengapit kumpulan elemen dalam tanda kurung siku, menggunakan titik koma (;) untuk membatasi elemen.
c = [7; 8; 9; 10; 11]MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
c =
7
8
9
10
11Membuat Matriks
Matriks adalah deretan angka dua dimensi.
Di MATLAB, matriks dibuat dengan memasukkan setiap baris sebagai urutan elemen yang dipisahkan oleh spasi atau koma, dan ujung baris dibatasi oleh titik koma. Misalnya, mari kita buat matriks 3-kali-3 sebagai -
m = [1 2 3; 4 5 6; 7 8 9]MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
m =
1 2 3
4 5 6
7 8 9MATLAB adalah program interaktif untuk komputasi numerik dan visualisasi data. Anda dapat memasukkan perintah dengan mengetiknya di MATLAB prompt '>>' diCommand Window.
Di bagian ini, kami akan memberikan daftar perintah MATLAB umum yang umum digunakan.
Perintah untuk Mengelola Sesi
MATLAB menyediakan berbagai perintah untuk mengelola sesi. Tabel berikut menyediakan semua perintah seperti itu -
| Perintah | Tujuan |
|---|---|
| clc | Menghapus jendela perintah. |
| bersih | Menghapus variabel dari memori. |
| ada | Memeriksa keberadaan file atau variabel. |
| global | Menyatakan variabel menjadi global. |
| Tolong | Mencari topik bantuan. |
| mencari | Mencari entri bantuan untuk kata kunci. |
| berhenti | Menghentikan MATLAB. |
| WHO | Daftar variabel saat ini. |
| siapa | Daftar variabel saat ini (tampilan panjang). |
Perintah untuk Bekerja dengan Sistem
MATLAB menyediakan berbagai perintah yang berguna untuk bekerja dengan sistem, seperti menyimpan pekerjaan saat ini di ruang kerja sebagai file dan memuat file nanti.
Ini juga menyediakan berbagai perintah untuk aktivitas terkait sistem lainnya seperti, menampilkan tanggal, membuat daftar file di direktori, menampilkan direktori saat ini, dll.
Tabel berikut menampilkan beberapa perintah terkait sistem yang umum digunakan -
| Perintah | Tujuan |
|---|---|
| CD | Mengubah direktori saat ini. |
| tanggal | Menampilkan tanggal sekarang. |
| menghapus | Menghapus file. |
| buku harian | Mengaktifkan / menonaktifkan perekaman file buku harian. |
| dir | Mencantumkan semua file di direktori saat ini. |
| beban | Memuat variabel ruang kerja dari file. |
| jalan | Menampilkan jalur pencarian. |
| pwd | Menampilkan direktori saat ini. |
| menyimpan | Menyimpan variabel ruang kerja dalam sebuah file. |
| Tipe | Menampilkan konten file. |
| apa | Daftar semua file MATLAB dalam direktori saat ini. |
| wklread.dll | Membaca file spreadsheet .wk1. |
Perintah Input dan Output
MATLAB menyediakan perintah terkait input dan output berikut -
| Perintah | Tujuan |
|---|---|
| disp | Menampilkan konten larik atau string. |
| fscanf.dll | Membaca data yang diformat dari file. |
| format | Mengontrol format tampilan layar. |
| fprintf | Melakukan penulisan yang diformat ke layar atau file. |
| memasukkan | Menampilkan prompt dan menunggu input. |
| ; | Menekan pencetakan layar. |
Itu fscanf dan fprintfperintah berperilaku seperti C scanf dan fungsi printf. Mereka mendukung kode format berikut -
| Kode Format | Tujuan |
|---|---|
| %s | Format sebagai string. |
| %d | Format sebagai bilangan bulat. |
| %f | Format sebagai nilai titik mengambang. |
| %e | Format sebagai nilai floating point dalam notasi ilmiah. |
| %g | Format dalam bentuk paling ringkas:% f atau% e. |
| \n | Sisipkan baris baru di string keluaran. |
| \t | Sisipkan tab di string keluaran. |
Fungsi format memiliki bentuk berikut yang digunakan untuk tampilan numerik -
| Fungsi Format | Tampilkan hingga |
|---|---|
| format pendek | Empat digit desimal (default). |
| format panjang | 16 digit desimal. |
| format pendek e | Lima digit ditambah eksponen. |
| format panjang e | 16 digit ditambah eksponen. |
| format bank | Dua digit desimal. |
| format + | Positif, negatif, atau nol. |
| format tikus | Pendekatan rasional. |
| format kompak | Menekan beberapa baris feed. |
| format longgar | Mengatur ulang ke mode tampilan yang kurang ringkas. |
Perintah Vektor, Matriks dan Array
Tabel berikut menunjukkan berbagai perintah yang digunakan untuk bekerja dengan array, matriks, dan vektor -
| Perintah | Tujuan |
|---|---|
| kucing | Menggabungkan array. |
| Temukan | Menemukan indeks elemen bukan nol. |
| panjangnya | Menghitung jumlah elemen. |
| linspace | Membuat vektor dengan jarak teratur. |
| logspace | Membuat vektor dengan spasi logaritmik. |
| maks | Mengembalikan elemen terbesar. |
| min | Mengembalikan elemen terkecil. |
| melecut | Produk dari setiap kolom. |
| membentuk kembali | Ubah ukuran. |
| ukuran | Menghitung ukuran array. |
| menyortir | Mengurutkan setiap kolom. |
| jumlah | Menjumlahkan setiap kolom. |
| mata | Membuat matriks identitas. |
| satu | Membuat array. |
| nol | Membuat larik nol. |
| menyeberang | Menghitung produk persilangan matriks. |
| dot | Menghitung produk titik matriks. |
| det | Menghitung determinan dari sebuah larik. |
| inv | Menghitung invers dari sebuah matriks. |
| pinv | Menghitung pseudoinverse dari sebuah matriks. |
| pangkat | Menghitung peringkat matriks. |
| rref | Menghitung bentuk eselon baris tereduksi. |
| sel | Membuat array sel. |
| celldisp | Menampilkan array sel. |
| plot sel | Menampilkan representasi grafis dari larik sel. |
| num2cell | Mengonversi larik numerik menjadi larik sel. |
| Sepakat | Cocok dengan daftar masukan dan keluaran. |
| iscell | Mengidentifikasi array sel. |
Perintah Plotting
MATLAB menyediakan banyak perintah untuk merencanakan grafik. Tabel berikut menunjukkan beberapa perintah yang umum digunakan untuk plotting -
| Perintah | Tujuan |
|---|---|
| sumbu | Tetapkan batas sumbu. |
| fplot.dll | Plot fungsi yang cerdas. |
| jaringan | Menampilkan garis kisi. |
| merencanakan | Menghasilkan plot xy. |
| mencetak | Mencetak plot atau menyimpan plot ke file. |
| judul | Menempatkan teks di atas plot. |
| xlabel | Menambahkan label teks ke sumbu x. |
| ylabel | Menambahkan label teks ke sumbu y. |
| sumbu | Membuat objek sumbu. |
| Menutup | Menutup plot saat ini. |
| tutup semua | Menutup semua plot. |
| angka | Membuka jendela gambar baru. |
| gtext | Memungkinkan penempatan label dengan mouse. |
| memegang | Membekukan plot saat ini. |
| legenda | Penempatan legenda dengan mouse. |
| menyegarkan | Menggambar ulang jendela gambar saat ini. |
| set | Menentukan properti objek seperti sumbu. |
| subplot | Membuat plot di subwindows. |
| teks | Menempatkan string dalam gambar. |
| batang | Membuat diagram batang. |
| loglog | Membuat plot log-log. |
| kutub | Membuat plot kutub. |
| semilogx | Membuat plot semilog. (absis logaritmik). |
| semilogi | Membuat plot semilog. (ordinat logaritmik). |
| tangga | Membuat plot tangga. |
| batang | Membuat plot batang. |
Sejauh ini, kami telah menggunakan lingkungan MATLAB sebagai kalkulator. Namun, MATLAB juga merupakan bahasa pemrograman yang kuat, serta lingkungan komputasi yang interaktif.
Pada bab sebelumnya, Anda telah mempelajari cara memasukkan perintah dari command prompt MATLAB. MATLAB juga memungkinkan Anda untuk menulis serangkaian perintah ke dalam file dan mengeksekusi file sebagai unit lengkap, seperti menulis fungsi dan memanggilnya.
File M
MATLAB memungkinkan penulisan dua jenis file program -
Scripts - file script adalah file program dengan .m extension. Dalam file ini, Anda menulis serangkaian perintah, yang ingin Anda jalankan bersama. Skrip tidak menerima masukan dan tidak mengembalikan keluaran apa pun. Mereka mengoperasikan data di ruang kerja.
Functions - file fungsi juga file program dengan .m extension. Fungsi dapat menerima masukan dan mengembalikan keluaran. Variabel internal bersifat lokal ke fungsi.
Anda dapat menggunakan editor MATLAB atau editor teks lainnya untuk membuat file .mfile. Pada bagian ini, kita akan membahas file script. File skrip berisi beberapa baris berurutan dari perintah MATLAB dan pemanggilan fungsi. Anda dapat menjalankan skrip dengan mengetikkan namanya di baris perintah.
Membuat dan Menjalankan File Script
Untuk membuat file skrip, Anda perlu menggunakan editor teks. Anda dapat membuka editor MATLAB dengan dua cara -
- Menggunakan command prompt
- Menggunakan IDE
Jika Anda menggunakan prompt perintah, ketik editdi prompt perintah. Ini akan membuka editor. Anda bisa langsung mengetikedit dan kemudian nama file (dengan ekstensi .m)
edit
Or
edit <filename>Perintah di atas akan membuat file dalam direktori MATLAB default. Jika Anda ingin menyimpan semua file program dalam folder tertentu, maka Anda harus menyediakan seluruh jalur.
Mari kita buat folder bernama progs. Ketik perintah berikut di prompt perintah (>>) -
mkdir progs % create directory progs under default directory
chdir progs % changing the current directory to progs
edit prog1.m % creating an m file named prog1.mJika Anda membuat file untuk pertama kalinya, MATLAB meminta Anda untuk mengkonfirmasinya. Klik Yes.
Alternatifnya, jika Anda menggunakan IDE, pilih NEW -> Script. Ini juga membuka editor dan membuat file bernama Untitled. Anda dapat memberi nama dan menyimpan file setelah mengetik kode.
Ketik kode berikut di editor -
NoOfStudents = 6000;
TeachingStaff = 150;
NonTeachingStaff = 20;
Total = NoOfStudents + TeachingStaff ...
+ NonTeachingStaff;
disp(Total);Setelah membuat dan menyimpan file, Anda dapat menjalankannya dengan dua cara -
Mengklik Run pada jendela editor atau
Cukup ketikkan nama file (tanpa ekstensi) di command prompt: >> prog1
Prompt jendela perintah menampilkan hasilnya -
6170Contoh
Buat file script, dan ketik kode berikut -
a = 5; b = 7;
c = a + b
d = c + sin(b)
e = 5 * d
f = exp(-d)Ketika kode di atas dikompilasi dan dijalankan, itu menghasilkan hasil sebagai berikut -
c = 12
d = 12.657
e = 63.285
f = 3.1852e-06MATLAB tidak memerlukan deklarasi tipe atau pernyataan dimensi apa pun. Setiap kali MATLAB menemukan nama variabel baru, itu membuat variabel dan mengalokasikan ruang memori yang sesuai.
Jika variabel sudah ada, MATLAB mengganti konten asli dengan konten baru dan mengalokasikan ruang penyimpanan baru, jika perlu.
Sebagai contoh,
Total = 42Pernyataan di atas membuat matriks 1-oleh-1 bernama 'Total' dan menyimpan nilai 42 di dalamnya.
Jenis Data Tersedia di MATLAB
MATLAB menyediakan 15 tipe data fundamental. Setiap tipe data menyimpan data yang berbentuk matriks atau larik. Ukuran matriks atau larik ini minimal 0-kali-0 dan dapat berkembang menjadi matriks atau larik dengan ukuran berapa pun.
Tabel berikut menunjukkan tipe data yang paling umum digunakan di MATLAB -
| Sr.No. | Tipe & Deskripsi Data |
|---|---|
| 1 | int8 Integer bertanda 8-bit |
| 2 | uint8 Integer 8-bit unsigned |
| 3 | int16 Integer bertanda tangan 16-bit |
| 4 | uint16 Integer 16-bit unsigned |
| 5 | int32 Integer bertanda tangan 32-bit |
| 6 | uint32 Integer 32-bit unsigned |
| 7 | int64 Integer 64-bit |
| 8 | uint64 Integer 64-bit unsigned |
| 9 | single data numerik presisi tunggal |
| 10 | double data numerik presisi ganda |
| 11 | logical nilai logika 1 atau 0, masing-masing mewakili benar dan salah |
| 12 | char data karakter (string disimpan sebagai vektor karakter) |
| 13 | cell array larik sel yang diindeks, masing-masing mampu menyimpan larik dengan dimensi dan tipe data yang berbeda |
| 14 | structure Struktur mirip C, setiap struktur memiliki bidang bernama yang mampu menyimpan larik dengan dimensi dan tipe data yang berbeda |
| 15 | function handle penunjuk ke suatu fungsi |
| 16 | user classes objek yang dibangun dari kelas yang ditentukan pengguna |
| 17 | java classes objek yang dibangun dari kelas Java |
Contoh
Buat file skrip dengan kode berikut -
str = 'Hello World!'
n = 2345
d = double(n)
un = uint32(789.50)
rn = 5678.92347
c = int32(rn)Ketika kode di atas dikompilasi dan dijalankan, itu menghasilkan hasil sebagai berikut -
str = Hello World!
n = 2345
d = 2345
un = 790
rn = 5678.9
c = 5679Konversi Jenis Data
MATLAB menyediakan berbagai fungsi untuk mengkonversi, nilai dari satu tipe data ke tipe lainnya. Tabel berikut menunjukkan fungsi konversi tipe data -
| Fungsi | Tujuan |
|---|---|
| arang | Ubah ke array karakter (string) |
| int2str | Ubah data integer menjadi string |
| mat2str | Ubah matriks menjadi string |
| num2str | Ubah angka menjadi string |
| str2double | Ubah string menjadi nilai presisi ganda |
| str2num | Ubah string menjadi angka |
| native2unicode.dll | Ubah byte numerik menjadi karakter Unicode |
| unicode2native | Ubah karakter Unicode menjadi byte numerik |
| base2dec | Ubah string angka dasar N menjadi angka desimal |
| bin2dec | Ubah string angka biner menjadi angka desimal |
| dec2base | Ubah desimal menjadi bilangan basis N dalam string |
| dec2bin | Ubah desimal menjadi bilangan biner dalam string |
| dec2hex | Ubah desimal menjadi bilangan heksadesimal dalam string |
| hex2dec | Ubah string angka heksadesimal menjadi angka desimal |
| hex2num | Ubah string angka heksadesimal menjadi angka presisi ganda |
| num2hex | Ubah single dan double menjadi string heksadesimal IEEE |
| cell2mat | Ubah larik sel menjadi larik numerik |
| cell2struct | Ubah larik sel menjadi larik struktur |
| cellstr | Buat array sel string dari array karakter |
| mat2cell | Mengonversi larik menjadi larik sel dengan ukuran sel yang berpotensi berbeda |
| num2cell | Mengonversi larik menjadi larik sel dengan sel berukuran konsisten |
| struct2cell | Ubah struktur menjadi larik sel |
Penentuan Jenis Data
MATLAB menyediakan berbagai fungsi untuk mengidentifikasi tipe data variabel.
Tabel berikut menyediakan fungsi untuk menentukan tipe data variabel -
| Fungsi | Tujuan |
|---|---|
| adalah | Deteksi status |
| adalah | Tentukan apakah input adalah objek dari kelas yang ditentukan |
| iscell | Tentukan apakah masukan adalah larik sel |
| iscellstr | Tentukan apakah masukan adalah larik sel string |
| ischar | Tentukan apakah item adalah array karakter |
| isfield | Tentukan apakah masukan adalah bidang larik struktur |
| terapung | Tentukan apakah input berupa array floating-point |
| ishghandle | Benar untuk menangani objek Menangani Grafik |
| isinteger | Tentukan apakah input adalah array integer |
| isjava | Tentukan apakah masukan adalah objek Java |
| islogical | Tentukan apakah masukan adalah larik logis |
| isnumerik | Tentukan apakah masukan berupa larik numerik |
| isobject | Tentukan apakah input adalah objek MATLAB |
| adalah nyata | Periksa apakah masukan adalah larik nyata |
| isscalar.dll | Tentukan apakah masukan adalah skalar |
| isstr | Tentukan apakah masukan berupa larik karakter |
| isstruct | Tentukan apakah masukan adalah larik struktur |
| isvector | Tentukan apakah masukan adalah vektor |
| kelas | Tentukan kelas objek |
| validateattributes | Periksa validitas array |
| siapa | Buat daftar variabel di ruang kerja, dengan ukuran dan jenis |
Contoh
Buat file skrip dengan kode berikut -
x = 3
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
x = 23.54
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
x = [1 2 3]
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
x = 'Hello'
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)Saat Anda menjalankan file, ini menghasilkan hasil sebagai berikut -
x = 3
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x = 23.540
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x =
1 2 3
ans = 0
ans = 1
ans = 1
ans = 0
x = Hello
ans = 0
ans = 0
ans = 1
ans = 0
ans = 0Operator adalah simbol yang memberi tahu kompiler untuk melakukan manipulasi matematika atau logika tertentu. MATLAB dirancang untuk beroperasi terutama pada seluruh matriks dan array. Oleh karena itu, operator di MATLAB bekerja pada data skalar dan non-skalar. MATLAB memungkinkan jenis operasi dasar berikut -
- Operator Aritmatika
- Operator Relasional
- Operator Logis
- Operasi Bitwise
- Atur Operasi
Operator Aritmatika
MATLAB memungkinkan dua jenis operasi aritmatika -
- Operasi aritmatika matriks
- Operasi aritmatika array
Operasi aritmatika matriks sama seperti yang didefinisikan dalam aljabar linier. Operasi array dijalankan elemen demi elemen, baik pada array satu dimensi maupun multidimensi.
Operator matriks dan operator array dibedakan oleh simbol titik (.). Namun, karena operasi penjumlahan dan pengurangan sama untuk matriks dan array, operatornya sama untuk kedua kasus. Tabel berikut memberikan penjelasan singkat tentang operator -
Tunjukkan Contoh
| Sr.No. | Operator & Deskripsi |
|---|---|
| 1 | + Penambahan atau plus unary. A + B menambahkan nilai yang disimpan dalam variabel A dan B. A dan B harus memiliki ukuran yang sama, kecuali salah satunya adalah skalar. Skalar dapat ditambahkan ke matriks dengan ukuran berapa pun. |
| 2 | - Pengurangan atau minus unary. AB mengurangi nilai B dari A. A dan B harus memiliki ukuran yang sama, kecuali salah satunya adalah skalar. Skalar dapat dikurangi dari matriks dengan ukuran berapa pun. |
| 3 | * Perkalian matriks. C = A * B adalah produk aljabar linier dari matriks A dan B. Lebih tepatnya,
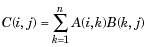
Untuk non-skalar A dan B, jumlah kolom A harus sama dengan jumlah baris B. Skalar dapat mengalikan matriks dengan ukuran berapa pun. |
| 4 | .* Perkalian array. A. * B adalah produk elemen demi elemen dari array A dan B. A dan B harus memiliki ukuran yang sama, kecuali salah satunya adalah skalar. |
| 5 | / Pembagian kanan garis miring atau matriks. B / A kira-kira sama dengan B * inv (A). Lebih tepatnya, B / A = (A '\ B') '. |
| 6 | ./ Pembagian kanan array. A./B adalah matriks dengan elemen A (i, j) / B (i, j). A dan B harus memiliki ukuran yang sama, kecuali salah satunya adalah skalar. |
| 7 | \ Garis miring terbalik atau pembagian kiri matriks. Jika A adalah matriks persegi, A \ B kira-kira sama dengan inv (A) * B, kecuali jika dihitung dengan cara yang berbeda. Jika A adalah n-by-n matriks dan B adalah vektor kolom dengan komponen n, atau matriks dengan beberapa kolom tersebut, maka X = A \ B adalah solusi untuk persamaan AX = B . Pesan peringatan ditampilkan jika skala A buruk atau hampir tunggal. |
| 8 | .\ Divisi kiri array. A. \ B adalah matriks dengan elemen B (i, j) / A (i, j). A dan B harus memiliki ukuran yang sama, kecuali salah satunya adalah skalar. |
| 9 | ^ Kekuatan matriks. X ^ p adalah X pangkat p, jika p adalah skalar. Jika p adalah bilangan bulat, daya dihitung dengan kuadrat berulang. Jika bilangan bulatnya negatif, X dibalik terlebih dahulu. Untuk nilai p lain, perhitungannya melibatkan nilai eigen dan vektor eigen, sehingga jika [V, D] = eig (X), maka X ^ p = V * D. ^ p / V. |
| 10 | .^ Kekuatan array. A. ^ B adalah matriks dengan elemen A (i, j) pangkat B (i, j). A dan B harus memiliki ukuran yang sama, kecuali salah satunya adalah skalar. |
| 11 | ' Transpos matriks. A 'adalah transpos aljabar linier dari A. Untuk matriks kompleks, ini adalah transpos konjugat kompleks. |
| 12 | .' Transpose array. SEBUAH.' adalah transpos array dari A. Untuk matriks kompleks, ini tidak melibatkan konjugasi. |
Operator Relasional
Operator relasional juga dapat bekerja pada data skalar dan non-skalar. Operator relasional untuk array melakukan perbandingan elemen-demi-elemen antara dua array dan mengembalikan array logis dengan ukuran yang sama, dengan elemen yang disetel ke logika 1 (true) di mana relasinya benar dan elemen disetel ke logika 0 (salah) di mana itu berada tidak.
Tabel berikut menunjukkan operator relasional yang tersedia di MATLAB -
Tunjukkan Contoh
| Sr.No. | Operator & Deskripsi |
|---|---|
| 1 | < Kurang dari |
| 2 | <= Kurang dari atau sama dengan |
| 3 | > Lebih besar dari |
| 4 | >= Lebih dari atau sama dengan |
| 5 | == Sama dengan |
| 6 | ~= Tidak sebanding dengan |
Operator Logis
MATLAB menawarkan dua jenis operator dan fungsi logika -
Elemen-bijaksana - Operator ini beroperasi pada elemen yang sesuai dari array logis.
Sirkuit pendek - Operator ini beroperasi pada skalar dan, ekspresi logis.
Operator logika berdasarkan elemen mengoperasikan elemen demi elemen pada array logis. Simbol &, |, dan ~ adalah operator larik logika AND, OR, dan NOT.
Operator logika sirkuit pendek memungkinkan hubungan pendek pada operasi logis. Simbol && dan || adalah operator hubung singkat logis AND dan OR.
Tunjukkan Contoh
Operasi Bitwise
Operator bitwise bekerja pada bit dan melakukan operasi bit demi bit. Tabel kebenaran untuk &, |, dan ^ adalah sebagai berikut -
| p | q | p & q | p | q | p ^ q |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
Asumsikan jika A = 60; dan B = 13; Sekarang dalam format biner akan menjadi sebagai berikut -
A = 0011 1100
B = 0000 1101
-----------------
A&B = 0000 1100
A | B = 0011 1101
A ^ B = 0011 0001
~ A = 1100 0011
MATLAB menyediakan berbagai fungsi untuk operasi bit-bijaksana seperti operasi 'bitwise dan', 'bitwise atau' dan 'bitwise not', operasi shift, dll.
Tabel berikut menunjukkan operasi bitwise yang umum digunakan -
Tunjukkan Contoh
| Fungsi | Tujuan |
|---|---|
| bitand (a, b) | Sedikit demi sedikit AND dari bilangan bulat a dan b |
| bitcmp (a) | Pelengkap yang bijak dari a |
| bitget (a, pos) | Dapatkan bit pada pos posisi yang ditentukan , dalam array integer a |
| bitor (a, b) | Bit-bijaksana OR dari bilangan bulat a dan b |
| bitset (a, pos) | Setel bit pada pos lokasi tertentu dari a |
| bitshift (a, k) | Mengembalikan a yang digeser ke kiri dengan k bit, setara dengan mengalikan dengan 2 k . Nilai negatif k sesuai dengan menggeser bit ke kanan atau membagi dengan 2 | k | dan pembulatan ke bilangan bulat terdekat menuju tak terbatas negatif. Setiap bit luapan terpotong. |
| bitxor (a, b) | XOR bit-bit dari bilangan bulat a dan b |
| swapbytes | Tukar urutan byte |
Atur Operasi
MATLAB menyediakan berbagai fungsi untuk operasi himpunan, seperti penyatuan, persimpangan dan pengujian untuk keanggotaan set, dll.
Tabel berikut menunjukkan beberapa operasi set yang umum digunakan -
Tunjukkan Contoh
| Sr.No. | Deskripsi fungsi |
|---|---|
| 1 | intersect(A,B) Set persimpangan dua larik; mengembalikan nilai yang sama untuk A dan B. Nilai yang dikembalikan berada dalam urutan yang diurutkan. |
| 2 | intersect(A,B,'rows') Memperlakukan setiap baris A dan setiap baris B sebagai entitas tunggal dan mengembalikan baris yang sama untuk A dan B. Baris dari matriks yang dikembalikan berada dalam urutan yang diurutkan. |
| 3 | ismember(A,B) Mengembalikan larik berukuran sama dengan A, berisi 1 (benar) di mana elemen A ditemukan di B. Di tempat lain, mengembalikan 0 (salah). |
| 4 | ismember(A,B,'rows') Memperlakukan setiap baris A dan setiap baris B sebagai entitas tunggal dan mengembalikan vektor yang berisi 1 (benar) di mana baris matriks A juga baris B. Di tempat lain, ia mengembalikan 0 (salah). |
| 5 | issorted(A) Mengembalikan logika 1 (benar) jika elemen A dalam urutan yang diurutkan dan logika 0 (salah) sebaliknya. Input A bisa berupa vektor atau larik sel string N-by-1 atau 1-by-N.A is considered to be sorted if A dan keluaran dari sort (A) adalah sama. |
| 6 | issorted(A, 'rows') Mengembalikan logika 1 (benar) jika baris dari matriks dua dimensi A dalam urutan yang diurutkan, dan logika 0 (salah) sebaliknya. Matrix A is considered to be sorted if A dan keluaran dari pengurutan (A) sama. |
| 7 | setdiff(A,B) Menetapkan perbedaan dua larik; mengembalikan nilai di A yang bukan di B. Nilai dalam larik yang dikembalikan berada dalam urutan yang diurutkan. |
| 8 | setdiff(A,B,'rows') Memperlakukan setiap baris A dan setiap baris B sebagai entitas tunggal dan mengembalikan baris dari A yang tidak ada di B. Baris dari matriks yang dikembalikan berada dalam urutan yang diurutkan. Opsi 'baris' tidak mendukung larik sel. |
| 9 | setxor Menetapkan OR eksklusif dari dua larik |
| 10 | union Menetapkan gabungan dua larik |
| 11 | unique Nilai unik dalam array |
Struktur pengambilan keputusan mensyaratkan bahwa programmer harus menentukan satu atau lebih kondisi untuk dievaluasi atau diuji oleh program, bersama dengan pernyataan atau pernyataan yang akan dieksekusi jika kondisi ditentukan benar, dan secara opsional, pernyataan lain yang akan dieksekusi jika kondisi ditentukan sebagai salah.
Berikut ini adalah bentuk umum dari struktur pengambilan keputusan khas yang ditemukan di sebagian besar bahasa pemrograman -
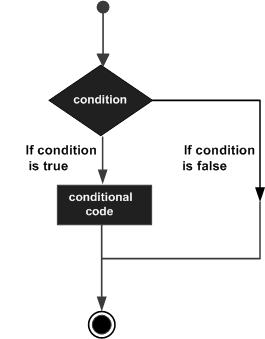
MATLAB memberikan jenis pernyataan pengambilan keputusan berikut. Klik tautan berikut untuk memeriksa detailnya -
| Sr.No. | Pernyataan & Deskripsi |
|---|---|
| 1 | jika ... pernyataan akhir Sebuah if ... end statement terdiri dari ekspresi boolean yang diikuti oleh satu atau beberapa pernyataan. |
| 2 | jika ... lain ... pernyataan akhir Sebuah if statement bisa diikuti dengan opsional else statement, yang dijalankan jika ekspresi boolean salah. |
| 3 | Jika ... elseif ... elseif ... lain ... pernyataan akhir Sebuah if Pernyataan dapat diikuti oleh satu (atau lebih) pilihan elseif... dan sebuah else pernyataan, yang sangat berguna untuk menguji berbagai kondisi. |
| 4 | pernyataan if bersarang Anda bisa menggunakannya if atau elseif pernyataan di dalam yang lain if atau elseif pernyataan. |
| 5 | pernyataan switch SEBUAH switch pernyataan memungkinkan variabel untuk diuji kesetaraan terhadap daftar nilai. |
| 6 | pernyataan saklar bersarang Anda bisa menggunakannya switch pernyataan di dalam yang lain switch pernyataan. |
Mungkin ada situasi ketika Anda perlu mengeksekusi blok kode beberapa kali. Secara umum, pernyataan dieksekusi secara berurutan. Pernyataan pertama dalam suatu fungsi dijalankan pertama, diikuti oleh yang kedua, dan seterusnya.
Bahasa pemrograman menyediakan berbagai struktur kontrol yang memungkinkan jalur eksekusi yang lebih rumit.
Pernyataan loop memungkinkan kita untuk mengeksekusi pernyataan atau sekelompok pernyataan beberapa kali dan berikut adalah bentuk umum dari pernyataan loop di sebagian besar bahasa pemrograman -
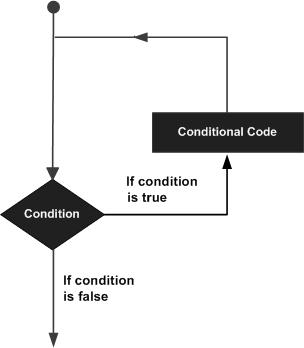
MATLAB menyediakan jenis loop berikut untuk menangani persyaratan perulangan. Klik tautan berikut untuk memeriksa detailnya -
| Sr.No. | Jenis & Deskripsi Loop |
|---|---|
| 1 | while loop Mengulangi pernyataan atau sekelompok pernyataan saat kondisi tertentu benar. Ini menguji kondisi sebelum menjalankan badan perulangan. |
| 2 | untuk loop Menjalankan urutan pernyataan beberapa kali dan menyingkat kode yang mengelola variabel loop. |
| 3 | loop bersarang Anda dapat menggunakan satu atau lebih loop di dalam loop lain. |
Pernyataan Kontrol Loop
Pernyataan kontrol loop mengubah eksekusi dari urutan normalnya. Saat eksekusi meninggalkan ruang lingkup, semua objek otomatis yang dibuat dalam lingkup itu dimusnahkan.
MATLAB mendukung pernyataan kontrol berikut. Klik tautan berikut untuk memeriksa detailnya.
| Sr.No. | Pernyataan & Deskripsi Kontrol |
|---|---|
| 1 | pernyataan istirahat Menghentikan loop pernyataan dan transfer eksekusi ke pernyataan segera setelah loop. |
| 2 | lanjutkan pernyataan Menyebabkan loop melewatkan sisa tubuhnya dan segera menguji ulang kondisinya sebelum mengulangi. |
Vektor adalah deretan angka satu dimensi. MATLAB memungkinkan pembuatan dua jenis vektor -
- Vektor baris
- Vektor kolom
Vektor Baris
Row vectors dibuat dengan mengapit kumpulan elemen dalam tanda kurung siku, menggunakan spasi atau koma untuk membatasi elemen.
r = [7 8 9 10 11]MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
r =
7 8 9 10 11Vektor Kolom
Column vectors dibuat dengan mengapit kumpulan elemen dalam tanda kurung siku, menggunakan titik koma untuk membatasi elemen.
c = [7; 8; 9; 10; 11]MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
c =
7
8
9
10
11Mereferensikan Elemen Vektor
Anda dapat mereferensikan satu atau lebih elemen vektor dengan beberapa cara. Komponen ke- i dari vektor v disebut sebagai v (i). Misalnya -
v = [ 1; 2; 3; 4; 5; 6]; % creating a column vector of 6 elements
v(3)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans = 3Saat Anda mereferensikan vektor dengan titik dua, seperti v (:), semua komponen vektor dicantumkan.
v = [ 1; 2; 3; 4; 5; 6]; % creating a column vector of 6 elements
v(:)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
1
2
3
4
5
6MATLAB memungkinkan Anda memilih berbagai elemen dari vektor.
Sebagai contoh, mari kita buat vektor baris rv dari 9 elemen, kemudian kita akan mereferensikan elemen 3 sampai 7 dengan menulisrv(3:7)dan buat vektor baru bernama sub_rv .
rv = [1 2 3 4 5 6 7 8 9];
sub_rv = rv(3:7)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
sub_rv =
3 4 5 6 7Operasi Vektor
Pada bagian ini, mari kita bahas operasi vektor berikut -
Penjumlahan dan Pengurangan Vektor
Perkalian Skalar Vektor
Mengubah urutan Vektor
Menambahkan Vektor
Besaran Vektor
Produk Vektor Dot
Vektor dengan Elemen Spasi Seragam
Matriks adalah deretan angka dua dimensi.
Di MATLAB, Anda membuat matriks dengan memasukkan elemen di setiap baris sebagai angka yang dipisahkan koma atau spasi dan menggunakan titik koma untuk menandai akhir setiap baris.
Misalnya, mari kita buat matriks 4 kali 5 a -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
a =
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8Mereferensikan Elemen Matriks
Untuk mereferensikan elemen di baris ke- m dan kolom ke- n , dari matriks mx , kita tulis -
mx(m, n);Misalnya, untuk merujuk ke elemen dalam 2 nd baris dan 5 th kolom, matriks yang , seperti yang dibuat dalam bagian terakhir, kita ketikkan -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(2,5)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans = 6Untuk referensi semua elemen dalam m th kolom kita tipe A (:, m).
Mari kita buat vektor kolom v, dari elemen-elemen baris ke- 4 dari matriks a -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
v = a(:,4)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
v =
4
5
6
7Anda juga dapat memilih elemen dalam m th melalui n th kolom, karena kita menulis ini -
a(:,m:n)Mari kita buat matriks yang lebih kecil dengan mengambil elemen dari kolom kedua dan ketiga -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
2 3
3 4
4 5
5 6Dengan cara yang sama, Anda bisa membuat sub-matriks yang mengambil sub-bagian dari matriks.
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
2 3
3 4
4 5
5 6Dengan cara yang sama, Anda bisa membuat sub-matriks yang mengambil sub-bagian dari matriks.
Sebagai contoh, mari kita buat sub-matriks sa yang mengambil bagian dalam dari a -
3 4 5
4 5 6Untuk melakukan ini, tulis -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
sa = a(2:3,2:4)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
sa =
3 4 5
4 5 6Menghapus Baris atau Kolom dalam Matriks
Anda dapat menghapus seluruh baris atau kolom dari sebuah matriks dengan menetapkan kumpulan tanda kurung siku [] kosong ke baris atau kolom tersebut. Pada dasarnya, [] menunjukkan larik kosong.
Misalnya, mari kita hapus baris keempat dari a -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a( 4 , : ) = []MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
a =
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7Selanjutnya, mari kita hapus kolom kelima dari a -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(: , 5)=[]MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
a =
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7Contoh
Dalam contoh ini, mari kita buat matriks 3-kali-3 m, lalu kita akan menyalin baris kedua dan ketiga dari matriks ini dua kali untuk membuat matriks 4-kali-3.
Buat file skrip dengan kode berikut -
a = [ 1 2 3 ; 4 5 6; 7 8 9];
new_mat = a([2,3,2,3],:)Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
new_mat =
4 5 6
7 8 9
4 5 6
7 8 9Operasi Matriks
Pada bagian ini, mari kita bahas operasi matriks dasar dan umum berikut ini -
Penjumlahan dan Pengurangan Matriks
Divisi Matriks
Operasi Skalar Matriks
Mengubah urutan Matriks
Matriks Penggabungan
Perkalian Matriks
Determinan Matriks
Pembalikan Matriks
Semua variabel dari semua tipe data di MATLAB adalah array multidimensi. Vektor adalah larik satu dimensi dan matriks adalah larik dua dimensi.
Kita telah membahas vektor dan matriks. Pada bab ini, kita akan membahas array multidimensi. Namun, sebelumnya, mari kita bahas beberapa jenis array khusus.
Array Khusus di MATLAB
Pada bagian ini, kita akan membahas beberapa fungsi yang membuat beberapa array khusus. Untuk semua fungsi ini, satu argumen membuat array persegi, argumen ganda membuat array persegi panjang.
Itu zeros() fungsi membuat array dari semua nol -
Misalnya -
zeros(5)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0Itu ones() fungsi membuat array dari semua yang -
Misalnya -
ones(4,3)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
1 1 1
1 1 1
1 1 1
1 1 1Itu eye() fungsi membuat matriks identitas.
Misalnya -
eye(4)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1Itu rand() fungsi membuat larik bilangan acak terdistribusi seragam di (0,1) -
Misalnya -
rand(3, 5)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
0.8147 0.9134 0.2785 0.9649 0.9572
0.9058 0.6324 0.5469 0.1576 0.4854
0.1270 0.0975 0.9575 0.9706 0.8003Kotak Ajaib
SEBUAH magic square adalah bujur sangkar yang menghasilkan jumlah yang sama, jika elemen-elemennya ditambahkan secara baris, kolom, atau diagonal.
Itu magic()fungsi membuat array persegi ajaib. Dibutuhkan argumen tunggal yang memberikan ukuran persegi. Argumennya harus skalar lebih besar dari atau sama dengan 3.
magic(4)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1Array Multidimensi
Array yang memiliki lebih dari dua dimensi disebut array multidimensi di MATLAB. Array multidimensi dalam MATLAB merupakan perpanjangan dari matriks dua dimensi normal.
Umumnya untuk menghasilkan array multidimensi, pertama kita membuat array dua dimensi dan memperluasnya.
Sebagai contoh, mari buat array dua dimensi a.
a = [7 9 5; 6 1 9; 4 3 2]MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
a =
7 9 5
6 1 9
4 3 2Larik a adalah larik 3-kali-3; kita dapat menambahkan dimensi ketiga ke a , dengan memberikan nilai seperti -
a(:, :, 2)= [ 1 2 3; 4 5 6; 7 8 9]MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
a =
ans(:,:,1) =
0 0 0
0 0 0
0 0 0
ans(:,:,2) =
1 2 3
4 5 6
7 8 9Kita juga bisa membuat array multidimensi menggunakan fungsi ones (), zeros () atau rand ().
Sebagai contoh,
b = rand(4,3,2)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
b(:,:,1) =
0.0344 0.7952 0.6463
0.4387 0.1869 0.7094
0.3816 0.4898 0.7547
0.7655 0.4456 0.2760
b(:,:,2) =
0.6797 0.4984 0.2238
0.6551 0.9597 0.7513
0.1626 0.3404 0.2551
0.1190 0.5853 0.5060Kita juga bisa menggunakan cat()berfungsi untuk membangun array multidimensi. Ini menggabungkan daftar array di sepanjang dimensi yang ditentukan -
Sintaks untuk fungsi cat () adalah -
B = cat(dim, A1, A2...)Dimana,
B adalah larik baru yang dibuat
A1 , A2 , ... adalah array yang akan digabungkan
redup adalah dimensi yang digunakan untuk menggabungkan array
Contoh
Buat file skrip dan ketikkan kode berikut ke dalamnya -
a = [9 8 7; 6 5 4; 3 2 1];
b = [1 2 3; 4 5 6; 7 8 9];
c = cat(3, a, b, [ 2 3 1; 4 7 8; 3 9 0])Saat Anda menjalankan file, ini akan menampilkan -
c(:,:,1) =
9 8 7
6 5 4
3 2 1
c(:,:,2) =
1 2 3
4 5 6
7 8 9
c(:,:,3) =
2 3 1
4 7 8
3 9 0Fungsi Array
MATLAB menyediakan fungsi berikut untuk mengurutkan, memutar, mengubah, membentuk kembali, atau menggeser konten array.
| Fungsi | Tujuan |
|---|---|
| panjangnya | Panjang vektor atau dimensi larik terbesar |
| ndims | Jumlah dimensi array |
| numel | Jumlah elemen array |
| ukuran | Dimensi array |
| iscolumn | Menentukan apakah masukan adalah vektor kolom |
| kosong | Menentukan apakah array kosong |
| ismatriks | Menentukan apakah masukan adalah matriks |
| isrow | Menentukan apakah masukan adalah vektor baris |
| isscalar.dll | Menentukan apakah masukan adalah skalar |
| isvector | Menentukan apakah masukan adalah vektor |
| blkdiag.dll | Membangun matriks blok diagonal dari argumen masukan |
| perpindahan tempat | Menggeser array secara melingkar |
| ctranspose | Transpos konjugat kompleks |
| diag | Matriks diagonal dan diagonal matriks |
| flipdim | Membalik array sepanjang dimensi yang ditentukan |
| fliplr | Membalik matriks dari kiri ke kanan |
| flipud | Membalik matriks ke atas ke bawah |
| ipermute | Membalikkan dimensi permute dari array ND |
| menukar urutan | Mengatur ulang dimensi larik ND |
| repmat | Replikasi dan susunan petak |
| membentuk kembali | Membentuk ulang larik |
| membusuk90 | Memutar matriks 90 derajat |
| shiftdim.dll | Menggeser dimensi |
| disortir | Menentukan apakah elemen set dalam urutan yang diurutkan |
| menyortir | Mengurutkan elemen array dalam urutan naik atau turun |
| sortrows | Mengurutkan baris dalam urutan menaik |
| meremas | Menghapus dimensi tunggal |
| mengubah urutan | Mengubah urutan |
| vektorisasi | Vektorisasi ekspresi |
Contoh
Contoh berikut menggambarkan beberapa fungsi yang disebutkan di atas.
Length, Dimension and Number of elements −
Buat file skrip dan ketikkan kode berikut ke dalamnya -
x = [7.1, 3.4, 7.2, 28/4, 3.6, 17, 9.4, 8.9];
length(x) % length of x vector
y = rand(3, 4, 5, 2);
ndims(y) % no of dimensions in array y
s = ['Zara', 'Nuha', 'Shamim', 'Riz', 'Shadab'];
numel(s) % no of elements in sSaat Anda menjalankan file, ini akan menampilkan hasil berikut -
ans = 8
ans = 4
ans = 23Circular Shifting of the Array Elements −
Buat file skrip dan ketikkan kode berikut ke dalamnya -
a = [1 2 3; 4 5 6; 7 8 9] % the original array a
b = circshift(a,1) % circular shift first dimension values down by 1.
c = circshift(a,[1 -1]) % circular shift first dimension values % down by 1
% and second dimension values to the left % by 1.Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
a =
1 2 3
4 5 6
7 8 9
b =
7 8 9
1 2 3
4 5 6
c =
8 9 7
2 3 1
5 6 4Menyortir Array
Buat file skrip dan ketikkan kode berikut ke dalamnya -
v = [ 23 45 12 9 5 0 19 17] % horizontal vector
sort(v) % sorting v
m = [2 6 4; 5 3 9; 2 0 1] % two dimensional array
sort(m, 1) % sorting m along the row
sort(m, 2) % sorting m along the columnSaat Anda menjalankan file, ini akan menampilkan hasil berikut -
v =
23 45 12 9 5 0 19 17
ans =
0 5 9 12 17 19 23 45
m =
2 6 4
5 3 9
2 0 1
ans =
2 0 1
2 3 4
5 6 9
ans =
2 4 6
3 5 9
0 1 2Array Sel
Larik sel adalah larik sel yang diindeks di mana setiap sel dapat menyimpan larik dengan dimensi dan tipe data yang berbeda.
Itu cellfungsi digunakan untuk membuat array sel. Sintaks untuk fungsi sel adalah -
C = cell(dim)
C = cell(dim1,...,dimN)
D = cell(obj)Dimana,
C adalah larik sel;
dim adalah bilangan bulat skalar atau vektor bilangan bulat yang menentukan dimensi larik sel C;
dim1, ..., dimN adalah bilangan bulat skalar yang menentukan dimensi C;
obj adalah Salah satu dari berikut -
- Array atau objek Java
- Array .NET berjenis System.String atau System.Object
Contoh
Buat file skrip dan ketikkan kode berikut ke dalamnya -
c = cell(2, 5);
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5}Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
c =
{
[1,1] = Red
[2,1] = 1
[1,2] = Blue
[2,2] = 2
[1,3] = Green
[2,3] = 3
[1,4] = Yellow
[2,4] = 4
[1,5] = White
[2,5] = 5
}Mengakses Data dalam Array Sel
Ada dua cara untuk merujuk ke elemen array sel -
- Mengapit indeks dalam tanda kurung pertama (), untuk merujuk ke kumpulan sel
- Mengapit indeks dalam tanda kurung kurawal {}, untuk merujuk ke data di dalam sel individu
Saat Anda mengapit indeks dalam tanda kurung pertama, ini merujuk ke kumpulan sel.
Indeks larik sel dalam tanda kurung mulus mengacu pada kumpulan sel.
Misalnya -
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c(1:2,1:2)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
{
[1,1] = Red
[2,1] = 1
[1,2] = Blue
[2,2] = 2
}Anda juga dapat mengakses konten sel dengan mengindeks dengan tanda kurung kurawal.
Misalnya -
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c{1, 2:4}MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans = Blue
ans = Green
ans = YellowItu colon(:)adalah salah satu operator paling berguna di MATLAB. Ini digunakan untuk membuat vektor, array subskrip, danspecify for iterations.
Jika Anda ingin membuat vektor baris, yang berisi bilangan bulat dari 1 hingga 10, Anda menulis -
1:10MATLAB mengeksekusi pernyataan dan mengembalikan vektor baris yang berisi bilangan bulat dari 1 hingga 10 -
ans =
1 2 3 4 5 6 7 8 9 10Jika Anda ingin menentukan nilai kenaikan selain dari satu, misalnya -
100: -5: 50MATLAB menjalankan pernyataan dan mengembalikan hasil berikut -
ans =
100 95 90 85 80 75 70 65 60 55 50Mari kita ambil contoh lain -
0:pi/8:piMATLAB menjalankan pernyataan dan mengembalikan hasil berikut -
ans =
Columns 1 through 7
0 0.3927 0.7854 1.1781 1.5708 1.9635 2.3562
Columns 8 through 9
2.7489 3.1416Anda dapat menggunakan operator titik dua untuk membuat vektor indeks untuk memilih baris, kolom, atau elemen array.
Tabel berikut menjelaskan penggunaannya untuk tujuan ini (mari kita memiliki matriks A) -
| Format | Tujuan |
|---|---|
| A(:,j) | adalah kolom ke-j dari A. |
| A(i,:) | adalah baris ke-i dari A. |
| A(:,:) | adalah larik dua dimensi yang setara. Untuk matriks, nilainya sama dengan A. |
| A(j:k) | adalah A (j), A (j + 1), ..., A (k). |
| A(:,j:k) | adalah A (:, j), A (:, j + 1), ..., A (:, k). |
| A(:,:,k) | adalah halaman ke- k dari larik tiga dimensi A. |
| A(i,j,k,:) | adalah vektor dalam larik empat dimensi A. Vektor tersebut meliputi A (i, j, k, 1), A (i, j, k, 2), A (i, j, k, 3), dan seterusnya. |
| A(:) | adalah semua elemen A, dianggap sebagai satu kolom. Di sisi kiri pernyataan tugas, A (:) mengisi A, mempertahankan bentuknya dari sebelumnya. Dalam hal ini, sisi kanan harus mengandung jumlah elemen yang sama dengan A. |
Contoh
Buat file skrip dan ketik kode berikut di dalamnya -
A = [1 2 3 4; 4 5 6 7; 7 8 9 10]
A(:,2) % second column of A
A(:,2:3) % second and third column of A
A(2:3,2:3) % second and third rows and second and third columnsSaat Anda menjalankan file, ini akan menampilkan hasil berikut -
A =
1 2 3 4
4 5 6 7
7 8 9 10
ans =
2
5
8
ans =
2 3
5 6
8 9
ans =
5 6
8 9MATLAB mendukung berbagai kelas numerik yang mencakup bilangan bulat bertanda dan tidak bertanda tangan serta nomor floating-point presisi tunggal dan ganda. Secara default, MATLAB menyimpan semua nilai numerik sebagai angka floating point presisi ganda.
Anda dapat memilih untuk menyimpan angka atau deretan angka apa pun sebagai bilangan bulat atau sebagai angka presisi tunggal.
Semua tipe numerik mendukung operasi array dasar dan operasi matematika.
Konversi ke Berbagai Jenis Data Numerik
MATLAB menyediakan fungsi berikut untuk mengkonversi ke berbagai tipe data numerik -
| Fungsi | Tujuan |
|---|---|
| dua kali lipat | Mengonversi ke angka presisi ganda |
| tunggal | Mengonversi ke angka presisi tunggal |
| int8 | Mengonversi menjadi bilangan bulat bertanda 8-bit |
| int16 | Mengonversi menjadi bilangan bulat bertanda 16-bit |
| int32 | Mengonversi menjadi bilangan bulat bertanda 32-bit |
| int64 | Mengonversi menjadi bilangan bulat bertanda 64-bit |
| uint8 | Mengonversi menjadi integer tanpa tanda tangan 8-bit |
| uint16 | Mengonversi menjadi integer 16-bit unsigned |
| uint32 | Mengonversi menjadi integer 32-bit unsigned |
| uint64 | Mengonversi menjadi 64-bit unsigned integer |
Contoh
Buat file script dan ketik kode berikut -
x = single([5.32 3.47 6.28]) .* 7.5
x = double([5.32 3.47 6.28]) .* 7.5
x = int8([5.32 3.47 6.28]) .* 7.5
x = int16([5.32 3.47 6.28]) .* 7.5
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5Saat Anda menjalankan file, ini menunjukkan hasil sebagai berikut -
x =
39.900 26.025 47.100
x =
39.900 26.025 47.100
x =
38 23 45
x =
38 23 45
x =
38 23 45
x =
38 23 45Contoh
Mari kita kembangkan contoh sebelumnya sedikit lagi. Buat file script dan ketik kode berikut -
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5
x = num2cell(x)Saat Anda menjalankan file, ini menunjukkan hasil sebagai berikut -
x =
38 23 45
x =
38 23 45
x =
{
[1,1] = 38
[1,2] = 23
[1,3] = 45
}Integer Terkecil dan Terbesar
Fungsinya intmax() dan intmin() mengembalikan nilai maksimum dan minimum yang dapat direpresentasikan dengan semua jenis bilangan bulat.
Kedua fungsi tersebut menggunakan tipe data integer sebagai argumennya, misalnya, intmax (int8) atau intmin (int64) dan mengembalikan nilai maksimum dan minimum yang dapat Anda wakili dengan tipe data integer.
Contoh
Contoh berikut menggambarkan cara mendapatkan nilai bilangan bulat terkecil dan terbesar. Buat file skrip dan tulis kode berikut di dalamnya -
% displaying the smallest and largest signed integer data
str = 'The range for int8 is:\n\t%d to %d ';
sprintf(str, intmin('int8'), intmax('int8'))
str = 'The range for int16 is:\n\t%d to %d ';
sprintf(str, intmin('int16'), intmax('int16'))
str = 'The range for int32 is:\n\t%d to %d ';
sprintf(str, intmin('int32'), intmax('int32'))
str = 'The range for int64 is:\n\t%d to %d ';
sprintf(str, intmin('int64'), intmax('int64'))
% displaying the smallest and largest unsigned integer data
str = 'The range for uint8 is:\n\t%d to %d ';
sprintf(str, intmin('uint8'), intmax('uint8'))
str = 'The range for uint16 is:\n\t%d to %d ';
sprintf(str, intmin('uint16'), intmax('uint16'))
str = 'The range for uint32 is:\n\t%d to %d ';
sprintf(str, intmin('uint32'), intmax('uint32'))
str = 'The range for uint64 is:\n\t%d to %d ';
sprintf(str, intmin('uint64'), intmax('uint64'))Saat Anda menjalankan file, ini menunjukkan hasil sebagai berikut -
ans = The range for int8 is:
-128 to 127
ans = The range for int16 is:
-32768 to 32767
ans = The range for int32 is:
-2147483648 to 2147483647
ans = The range for int64 is:
0 to 0
ans = The range for uint8 is:
0 to 255
ans = The range for uint16 is:
0 to 65535
ans = The range for uint32 is:
0 to -1
ans = The range for uint64 is:
0 to 18446744073709551616Angka Floating Point Terkecil dan Terbesar
Fungsinya realmax() dan realmin() mengembalikan nilai maksimum dan minimum yang dapat direpresentasikan dengan angka floating point.
Kedua fungsi tersebut saat dipanggil dengan argumen 'single', mengembalikan nilai maksimum dan minimum yang dapat Anda wakili dengan tipe data presisi tunggal dan saat dipanggil dengan argumen 'double', kembalikan nilai maksimum dan minimum yang dapat Anda wakili tipe data presisi ganda.
Contoh
Contoh berikut mengilustrasikan cara mendapatkan bilangan floating point terkecil dan terbesar. Buat file skrip dan tulis kode berikut di dalamnya -
% displaying the smallest and largest single-precision
% floating point number
str = 'The range for single is:\n\t%g to %g and\n\t %g to %g';
sprintf(str, -realmax('single'), -realmin('single'), ...
realmin('single'), realmax('single'))
% displaying the smallest and largest double-precision
% floating point number
str = 'The range for double is:\n\t%g to %g and\n\t %g to %g';
sprintf(str, -realmax('double'), -realmin('double'), ...
realmin('double'), realmax('double'))Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
ans = The range for single is:
-3.40282e+38 to -1.17549e-38 and
1.17549e-38 to 3.40282e+38
ans = The range for double is:
-1.79769e+308 to -2.22507e-308 and
2.22507e-308 to 1.79769e+308Membuat string karakter cukup sederhana di MATLAB. Faktanya, kami telah menggunakannya berkali-kali. Misalnya, Anda mengetik berikut ini di prompt perintah -
my_string = 'Tutorials Point'MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
my_string = Tutorials PointMATLAB menganggap semua variabel sebagai array, dan string dianggap sebagai array karakter. Mari kita gunakanwhos perintah untuk memeriksa variabel yang dibuat di atas -
whosMATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
Name Size Bytes Class Attributes
my_string 1x16 32 charMenariknya, Anda dapat menggunakan fungsi konversi numerik seperti uint8 atau uint16untuk mengubah karakter dalam string menjadi kode numeriknya. Ituchar fungsi mengubah vektor integer kembali ke karakter -
Contoh
Buat file skrip dan ketikkan kode berikut ke dalamnya -
my_string = 'Tutorial''s Point';
str_ascii = uint8(my_string) % 8-bit ascii values
str_back_to_char= char(str_ascii)
str_16bit = uint16(my_string) % 16-bit ascii values
str_back_to_char = char(str_16bit)Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
str_ascii =
84 117 116 111 114 105 97 108 39 115 32 80 111 105 110 116
str_back_to_char = Tutorial's Point
str_16bit =
84 117 116 111 114 105 97 108 39 115 32 80 111 105 110 116
str_back_to_char = Tutorial's PointArray Karakter Persegi Panjang
String yang telah kita diskusikan sejauh ini adalah array karakter satu dimensi; Namun, kita perlu menyimpan lebih dari itu. Kita perlu menyimpan lebih banyak data tekstual dalam program kita. Ini dicapai dengan membuat array karakter persegi panjang.
Cara termudah untuk membuat larik karakter persegi panjang adalah dengan menggabungkan dua atau lebih larik karakter satu dimensi, baik secara vertikal maupun horizontal sesuai kebutuhan.
Anda dapat menggabungkan string secara vertikal dengan salah satu cara berikut -
Menggunakan operator penggabungan MATLAB []dan memisahkan setiap baris dengan titik koma (;). Harap diperhatikan bahwa dalam metode ini setiap baris harus mengandung jumlah karakter yang sama. Untuk string dengan panjang berbeda, Anda harus mengisi karakter spasi sesuai kebutuhan.
Menggunakan charfungsi. Jika string memiliki panjang yang berbeda, karakter mengisi string yang lebih pendek dengan trailing blank sehingga setiap baris memiliki jumlah karakter yang sama.
Contoh
Buat file skrip dan ketikkan kode berikut ke dalamnya -
doc_profile = ['Zara Ali '; ...
'Sr. Surgeon '; ...
'R N Tagore Cardiology Research Center']
doc_profile = char('Zara Ali', 'Sr. Surgeon', ...
'RN Tagore Cardiology Research Center')Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
doc_profile =
Zara Ali
Sr. Surgeon
R N Tagore Cardiology Research Center
doc_profile =
Zara Ali
Sr. Surgeon
RN Tagore Cardiology Research CenterAnda dapat menggabungkan string secara horizontal dengan salah satu cara berikut -
Menggunakan operator penggabungan MATLAB, []dan memisahkan string input dengan koma atau spasi. Metode ini mempertahankan spasi tambahan dalam larik input.
Menggunakan fungsi penggabungan string, strcat. Metode ini menghapus spasi tambahan di input.
Contoh
Buat file skrip dan ketikkan kode berikut ke dalamnya -
name = 'Zara Ali ';
position = 'Sr. Surgeon ';
worksAt = 'R N Tagore Cardiology Research Center';
profile = [name ', ' position ', ' worksAt]
profile = strcat(name, ', ', position, ', ', worksAt)Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
profile = Zara Ali , Sr. Surgeon , R N Tagore Cardiology Research Center
profile = Zara Ali,Sr. Surgeon,R N Tagore Cardiology Research CenterMenggabungkan String menjadi Array Sel
Dari diskusi kita sebelumnya, jelas bahwa menggabungkan string dengan panjang yang berbeda bisa jadi merepotkan karena semua string dalam array harus memiliki panjang yang sama. Kami telah menggunakan spasi kosong di akhir string untuk menyamakan panjangnya.
Namun, cara yang lebih efisien untuk menggabungkan string adalah dengan mengubah larik yang dihasilkan menjadi larik sel.
Larik sel MATLAB dapat menampung berbagai ukuran dan jenis data dalam larik. Array sel menyediakan cara yang lebih fleksibel untuk menyimpan string dengan panjang yang bervariasi.
Itu cellstr fungsi mengubah larik karakter menjadi larik sel string.
Contoh
Buat file skrip dan ketikkan kode berikut ke dalamnya -
name = 'Zara Ali ';
position = 'Sr. Surgeon ';
worksAt = 'R N Tagore Cardiology Research Center';
profile = char(name, position, worksAt);
profile = cellstr(profile);
disp(profile)Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
{
[1,1] = Zara Ali
[2,1] = Sr. Surgeon
[3,1] = R N Tagore Cardiology Research Center
}Fungsi String di MATLAB
MATLAB menyediakan banyak fungsi string yang membuat, menggabungkan, mengurai, membandingkan, dan memanipulasi string.
Tabel berikut memberikan penjelasan singkat tentang fungsi string di MATLAB -
| Fungsi | Tujuan |
|---|---|
| Fungsi untuk menyimpan teks dalam larik karakter, menggabungkan larik karakter, dll. | |
| kosong | Buat string karakter kosong |
| cellstr | Buat array sel string dari array karakter |
| arang | Ubah ke array karakter (string) |
| iscellstr | Tentukan apakah masukan adalah larik sel string |
| ischar | Tentukan apakah item adalah array karakter |
| sprintf | Format data menjadi string |
| strcat | Gabungkan string secara horizontal |
| strjoin | Gabungkan string dalam array sel menjadi string tunggal |
| Berfungsi untuk mengidentifikasi bagian string, mencari dan mengganti substring | |
| ischar | Tentukan apakah item adalah array karakter |
| isletter | Elemen larik yang merupakan huruf abjad |
| isspace | Elemen larik yang merupakan karakter spasi |
| isstrprop | Tentukan apakah string termasuk dalam kategori tertentu |
| sscanf | Membaca data yang diformat dari string |
| strfind | Temukan satu string di dalam string lainnya |
| strrep | Temukan dan ganti substring |
| strsplit.dll | Pisahkan string pada pembatas yang ditentukan |
| strtok | Bagian string yang dipilih |
| validatestring | Periksa validitas string teks |
| symvar | Tentukan variabel simbolik dalam ekspresi |
| regexp | Match regular expression (case sensitive) |
| regexpi | Match regular expression (case insensitive) |
| regexprep | Replace string using regular expression |
| regexptranslate | Translate string into regular expression |
| Functions for string comparison | |
| strcmp | Compare strings (case sensitive) |
| strcmpi | Compare strings (case insensitive) |
| strncmp | Compare first n characters of strings (case sensitive) |
| strncmpi | Compare first n characters of strings (case insensitive) |
| Functions for changing string to upper- or lowercase, creating or removing white space | |
| deblank | Strip trailing blanks from end of string |
| strtrim | Remove leading and trailing white space from string |
| lower | Convert string to lowercase |
| upper | Convert string to uppercase |
| strjust | Justify character array |
Examples
The following examples illustrate some of the above-mentioned string functions −
Formatting Strings
Create a script file and type the following code into it −
A = pi*1000*ones(1,5);
sprintf(' %f \n %.2f \n %+.2f \n %12.2f \n %012.2f \n', A)When you run the file, it displays the following result −
ans = 3141.592654
3141.59
+3141.59
3141.59
000003141.59Joining Strings
Create a script file and type the following code into it −
%cell array of strings
str_array = {'red','blue','green', 'yellow', 'orange'};
% Join strings in cell array into single string
str1 = strjoin(str_array, "-")
str2 = strjoin(str_array, ",")When you run the file, it displays the following result −
str1 = red-blue-green-yellow-orange
str2 = red,blue,green,yellow,orangeFinding and Replacing Strings
Create a script file and type the following code into it −
students = {'Zara Ali', 'Neha Bhatnagar', ...
'Monica Malik', 'Madhu Gautam', ...
'Madhu Sharma', 'Bhawna Sharma',...
'Nuha Ali', 'Reva Dutta', ...
'Sunaina Ali', 'Sofia Kabir'};
% The strrep function searches and replaces sub-string.
new_student = strrep(students(8), 'Reva', 'Poulomi')
% Display first names
first_names = strtok(students)When you run the file, it displays the following result −
new_student =
{
[1,1] = Poulomi Dutta
}
first_names =
{
[1,1] = Zara
[1,2] = Neha
[1,3] = Monica
[1,4] = Madhu
[1,5] = Madhu
[1,6] = Bhawna
[1,7] = Nuha
[1,8] = Reva
[1,9] = Sunaina
[1,10] = Sofia
}Comparing Strings
Create a script file and type the following code into it −
str1 = 'This is test'
str2 = 'This is text'
if (strcmp(str1, str2))
sprintf('%s and %s are equal', str1, str2)
else
sprintf('%s and %s are not equal', str1, str2)
endWhen you run the file, it displays the following result −
str1 = This is test
str2 = This is text
ans = This is test and This is text are not equalA function is a group of statements that together perform a task. In MATLAB, functions are defined in separate files. The name of the file and of the function should be the same.
Functions operate on variables within their own workspace, which is also called the local workspace, separate from the workspace you access at the MATLAB command prompt which is called the base workspace.
Functions can accept more than one input arguments and may return more than one output arguments.
Syntax of a function statement is −
function [out1,out2, ..., outN] = myfun(in1,in2,in3, ..., inN)Example
The following function named mymax should be written in a file named mymax.m. It takes five numbers as argument and returns the maximum of the numbers.
Create a function file, named mymax.m and type the following code in it −
function max = mymax(n1, n2, n3, n4, n5)
%This function calculates the maximum of the
% five numbers given as input
max = n1;
if(n2 > max)
max = n2;
end
if(n3 > max)
max = n3;
end
if(n4 > max)
max = n4;
end
if(n5 > max)
max = n5;
endThe first line of a function starts with the keyword function. It gives the name of the function and order of arguments. In our example, the mymax function has five input arguments and one output argument.
The comment lines that come right after the function statement provide the help text. These lines are printed when you type −
help mymaxMATLAB will execute the above statement and return the following result −
This function calculates the maximum of the
five numbers given as inputYou can call the function as −
mymax(34, 78, 89, 23, 11)MATLAB will execute the above statement and return the following result −
ans = 89Anonymous Functions
An anonymous function is like an inline function in traditional programming languages, defined within a single MATLAB statement. It consists of a single MATLAB expression and any number of input and output arguments.
You can define an anonymous function right at the MATLAB command line or within a function or script.
This way you can create simple functions without having to create a file for them.
The syntax for creating an anonymous function from an expression is
f = @(arglist)expressionExample
In this example, we will write an anonymous function named power, which will take two numbers as input and return first number raised to the power of the second number.
Create a script file and type the following code in it −
power = @(x, n) x.^n;
result1 = power(7, 3)
result2 = power(49, 0.5)
result3 = power(10, -10)
result4 = power (4.5, 1.5)When you run the file, it displays −
result1 = 343
result2 = 7
result3 = 1.0000e-10
result4 = 9.5459Primary and Sub-Functions
Any function other than an anonymous function must be defined within a file. Each function file contains a required primary function that appears first and any number of optional sub-functions that comes after the primary function and used by it.
Primary functions can be called from outside of the file that defines them, either from command line or from other functions, but sub-functions cannot be called from command line or other functions, outside the function file.
Sub-functions are visible only to the primary function and other sub-functions within the function file that defines them.
Example
Let us write a function named quadratic that would calculate the roots of a quadratic equation. The function would take three inputs, the quadratic co-efficient, the linear co-efficient and the constant term. It would return the roots.
The function file quadratic.m will contain the primary function quadratic and the sub-function disc, which calculates the discriminant.
Create a function file quadratic.m and type the following code in it −
function [x1,x2] = quadratic(a,b,c)
%this function returns the roots of
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficients of x2, x and the
%constant term
% It returns the roots
d = disc(a,b,c);
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of quadratic
function dis = disc(a,b,c)
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end % end of sub-functionYou can call the above function from command prompt as −
quadratic(2,4,-4)MATLAB will execute the above statement and return the following result −
ans = 0.7321Nested Functions
You can define functions within the body of another function. These are called nested functions. A nested function contains any or all of the components of any other function.
Nested functions are defined within the scope of another function and they share access to the containing function's workspace.
A nested function follows the following syntax −
function x = A(p1, p2)
...
B(p2)
function y = B(p3)
...
end
...
endExample
Let us rewrite the function quadratic, from previous example, however, this time the disc function will be a nested function.
Create a function file quadratic2.m and type the following code in it −
function [x1,x2] = quadratic2(a,b,c)
function disc % nested function
d = sqrt(b^2 - 4*a*c);
end % end of function disc
disc;
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of function quadratic2You can call the above function from command prompt as −
quadratic2(2,4,-4)MATLAB will execute the above statement and return the following result −
ans = 0.73205Private Functions
A private function is a primary function that is visible only to a limited group of other functions. If you do not want to expose the implementation of a function(s), you can create them as private functions.
Private functions reside in subfolders with the special name private.
They are visible only to functions in the parent folder.
Example
Let us rewrite the quadratic function. This time, however, the disc function calculating the discriminant, will be a private function.
Create a subfolder named private in working directory. Store the following function file disc.m in it −
function dis = disc(a,b,c)
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end % end of sub-functionCreate a function quadratic3.m in your working directory and type the following code in it −
function [x1,x2] = quadratic3(a,b,c)
%this function returns the roots of
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficient of x2, x and the
%constant term
% It returns the roots
d = disc(a,b,c);
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end % end of quadratic3You can call the above function from command prompt as −
quadratic3(2,4,-4)MATLAB will execute the above statement and return the following result −
ans = 0.73205Global Variables
Global variables can be shared by more than one function. For this, you need to declare the variable as global in all the functions.
If you want to access that variable from the base workspace, then declare the variable at the command line.
The global declaration must occur before the variable is actually used in a function. It is a good practice to use capital letters for the names of global variables to distinguish them from other variables.
Example
Let us create a function file named average.m and type the following code in it −
function avg = average(nums)
global TOTAL
avg = sum(nums)/TOTAL;
endCreate a script file and type the following code in it −
global TOTAL;
TOTAL = 10;
n = [34, 45, 25, 45, 33, 19, 40, 34, 38, 42];
av = average(n)When you run the file, it will display the following result −
av = 35.500Importing data in MATLAB means loading data from an external file. The importdata function allows loading various data files of different formats. It has the following five forms −
| Sr.No. | Function & Description |
|---|---|
| 1 | A = importdata(filename) Loads data into array A from the file denoted by filename. |
| 2 | A = importdata('-pastespecial') Loads data from the system clipboard rather than from a file. |
| 3 | A = importdata(___, delimiterIn) Interprets delimiterIn as the column separator in ASCII file, filename, or the clipboard data. You can use delimiterIn with any of the input arguments in the above syntaxes. |
| 4 | A = importdata(___, delimiterIn, headerlinesIn) Loads data from ASCII file, filename, or the clipboard, reading numeric data starting from line headerlinesIn+1. |
| 5 | [A, delimiterOut, headerlinesOut] = importdata(___) Returns the detected delimiter character for the input ASCII file in delimiterOut and the detected number of header lines in headerlinesOut, using any of the input arguments in the previous syntaxes. |
By default, Octave does not have support for importdata() function, so you will have to search and install this package to make following examples work with your Octave installation.
Example 1
Let us load and display an image file. Create a script file and type the following code in it −
filename = 'smile.jpg';
A = importdata(filename);
image(A);When you run the file, MATLAB displays the image file. However, you must store it in the current directory.

Example 2
In this example, we import a text file and specify Delimiter and Column Header. Let us create a space-delimited ASCII file with column headers, named weeklydata.txt.
Our text file weeklydata.txt looks like this −
SunDay MonDay TuesDay WednesDay ThursDay FriDay SaturDay
95.01 76.21 61.54 40.57 55.79 70.28 81.53
73.11 45.65 79.19 93.55 75.29 69.87 74.68
60.68 41.85 92.18 91.69 81.32 90.38 74.51
48.60 82.14 73.82 41.03 0.99 67.22 93.18
89.13 44.47 57.63 89.36 13.89 19.88 46.60Create a script file and type the following code in it −
filename = 'weeklydata.txt';
delimiterIn = ' ';
headerlinesIn = 1;
A = importdata(filename,delimiterIn,headerlinesIn);
% View data
for k = [1:7]
disp(A.colheaders{1, k})
disp(A.data(:, k))
disp(' ')
endWhen you run the file, it displays the following result −
SunDay
95.0100
73.1100
60.6800
48.6000
89.1300
MonDay
76.2100
45.6500
41.8500
82.1400
44.4700
TuesDay
61.5400
79.1900
92.1800
73.8200
57.6300
WednesDay
40.5700
93.5500
91.6900
41.0300
89.3600
ThursDay
55.7900
75.2900
81.3200
0.9900
13.8900
FriDay
70.2800
69.8700
90.3800
67.2200
19.8800
SaturDay
81.5300
74.6800
74.5100
93.1800
46.6000Contoh 3
Dalam contoh ini, mari kita mengimpor data dari clipboard.
Salin baris berikut ke clipboard -
Mathematics is simple
Buat file script dan ketik kode berikut -
A = importdata('-pastespecial')Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
A =
'Mathematics is simple'I / O File Tingkat Rendah
Fungsi importdata adalah fungsi tingkat tinggi. Fungsi I / O file tingkat rendah di MATLAB memungkinkan kontrol paling besar atas membaca atau menulis data ke file. Namun, fungsi ini memerlukan informasi yang lebih detail tentang file Anda agar berfungsi secara efisien.
MATLAB menyediakan fungsi berikut untuk operasi baca dan tulis pada tingkat byte atau karakter -
| Fungsi | Deskripsi |
|---|---|
| fclose | Tutup satu atau semua file yang terbuka |
| feof | Uji akhir file |
| ferror | Informasi tentang kesalahan I / O file |
| fgetl | Baca baris dari file, hapus karakter baris baru |
| gadget | Baca baris dari file, pertahankan karakter baris baru |
| pesolek | Buka file, atau dapatkan informasi tentang file yang terbuka |
| fprintf | Tulis data ke file teks |
| ketakutan | Membaca data dari file biner |
| frewind | Pindahkan indikator posisi file ke awal file yang terbuka |
| fscanf.dll | Membaca data dari file teks |
| fseek | Pindah ke posisi yang ditentukan dalam file |
| ftell | Posisi dalam file terbuka |
| fwrite | Tulis data ke file biner |
Impor File Data Teks dengan I / O Tingkat Rendah
MATLAB menyediakan fungsi berikut untuk impor file data teks tingkat rendah -
Itu fscanf fungsi membaca data yang diformat dalam teks atau file ASCII.
Itu fgetl dan fgets fungsi membaca satu baris file pada satu waktu, di mana karakter baris baru memisahkan setiap baris.
Itu fread fungsi membaca aliran data pada tingkat byte atau bit.
Contoh
Kami memiliki file data teks 'myfile.txt' yang disimpan di direktori kerja kami. File tersebut menyimpan data curah hujan selama tiga bulan; Juni, Juli dan Agustus untuk tahun 2012.
Data di myfile.txt berisi rangkaian pengukuran waktu, bulan, dan curah hujan yang berulang di lima tempat. Data header menyimpan jumlah bulan M; jadi kami memiliki M set pengukuran.
File tersebut terlihat seperti ini -
Rainfall Data
Months: June, July, August
M = 3
12:00:00
June-2012
17.21 28.52 39.78 16.55 23.67
19.15 0.35 17.57 NaN 12.01
17.92 28.49 17.40 17.06 11.09
9.59 9.33 NaN 0.31 0.23
10.46 13.17 NaN 14.89 19.33
20.97 19.50 17.65 14.45 14.00
18.23 10.34 17.95 16.46 19.34
09:10:02
July-2012
12.76 16.94 14.38 11.86 16.89
20.46 23.17 NaN 24.89 19.33
30.97 49.50 47.65 24.45 34.00
18.23 30.34 27.95 16.46 19.34
30.46 33.17 NaN 34.89 29.33
30.97 49.50 47.65 24.45 34.00
28.67 30.34 27.95 36.46 29.34
15:03:40
August-2012
17.09 16.55 19.59 17.25 19.22
17.54 11.45 13.48 22.55 24.01
NaN 21.19 25.85 25.05 27.21
26.79 24.98 12.23 16.99 18.67
17.54 11.45 13.48 22.55 24.01
NaN 21.19 25.85 25.05 27.21
26.79 24.98 12.23 16.99 18.67Kami akan mengimpor data dari file ini dan menampilkan data ini. Lakukan langkah-langkah berikut -
Buka file dengan fopen berfungsi dan mendapatkan pengenal file.
Jelaskan data dalam file dengan format specifiers, seperti '%s'untuk sebuah string,'%d'untuk integer, atau'%f'untuk bilangan floating-point.
Untuk melewati karakter literal dalam file, sertakan dalam deskripsi format. Untuk melewati bidang data, gunakan tanda bintang ('*') di penentu.
Misalnya, untuk membaca header dan mengembalikan nilai tunggal M, kita menulis -
M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);Secara default, fscanfmembaca data sesuai dengan deskripsi format kami hingga tidak menemukan kecocokan data, atau mencapai akhir file. Di sini kita akan menggunakan for loop untuk membaca 3 set data dan setiap kali akan membaca 7 baris dan 5 kolom.
Kami akan membuat struktur bernama mydata di ruang kerja untuk menyimpan data yang dibaca dari file. Struktur ini memiliki tiga bidang - waktu , bulan , dan susunan data hujan .
Buat file skrip dan ketik kode berikut di dalamnya -
filename = '/data/myfile.txt';
rows = 7;
cols = 5;
% open the file
fid = fopen(filename);
% read the file headers, find M (number of months)
M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);
% read each set of measurements
for n = 1:M
mydata(n).time = fscanf(fid, '%s', 1);
mydata(n).month = fscanf(fid, '%s', 1);
% fscanf fills the array in column order,
% so transpose the results
mydata(n).raindata = ...
fscanf(fid, '%f', [rows, cols]);
end
for n = 1:M
disp(mydata(n).time), disp(mydata(n).month)
disp(mydata(n).raindata)
end
% close the file
fclose(fid);Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
12:00:00
June-2012
17.2100 17.5700 11.0900 13.1700 14.4500
28.5200 NaN 9.5900 NaN 14.0000
39.7800 12.0100 9.3300 14.8900 18.2300
16.5500 17.9200 NaN 19.3300 10.3400
23.6700 28.4900 0.3100 20.9700 17.9500
19.1500 17.4000 0.2300 19.5000 16.4600
0.3500 17.0600 10.4600 17.6500 19.3400
09:10:02
July-2012
12.7600 NaN 34.0000 33.1700 24.4500
16.9400 24.8900 18.2300 NaN 34.0000
14.3800 19.3300 30.3400 34.8900 28.6700
11.8600 30.9700 27.9500 29.3300 30.3400
16.8900 49.5000 16.4600 30.9700 27.9500
20.4600 47.6500 19.3400 49.5000 36.4600
23.1700 24.4500 30.4600 47.6500 29.3400
15:03:40
August-2012
17.0900 13.4800 27.2100 11.4500 25.0500
16.5500 22.5500 26.7900 13.4800 27.2100
19.5900 24.0100 24.9800 22.5500 26.7900
17.2500 NaN 12.2300 24.0100 24.9800
19.2200 21.1900 16.9900 NaN 12.2300
17.5400 25.8500 18.6700 21.1900 16.9900
11.4500 25.0500 17.5400 25.8500 18.6700Ekspor data (atau keluaran) dalam MATLAB berarti menulis ke dalam file. MATLAB memungkinkan Anda untuk menggunakan data Anda di aplikasi lain yang membaca file ASCII. Untuk ini, MATLAB menyediakan beberapa opsi ekspor data.
Anda dapat membuat jenis file berikut -
File data ASCII berbentuk persegi dan dipisahkan dari larik.
File buku harian (atau log) penekanan tombol dan output teks yang dihasilkan.
File ASCII khusus yang menggunakan fungsi level rendah seperti fprintf.
MEX-file untuk mengakses rutinitas C / C ++ atau Fortran Anda yang menulis ke format file teks tertentu.
Selain itu, Anda juga dapat mengekspor data ke spreadsheet.
Ada dua cara untuk mengekspor larik numerik sebagai file data ASCII yang dipisahkan -
Menggunakan save fungsi dan menentukan -ascii kualifikasi
Menggunakan dlmwrite fungsi
Sintaks untuk menggunakan fungsi simpan adalah -
save my_data.out num_array -asciidi mana, my_data.out adalah file data ASCII yang dipisahkan dibuat, num_array adalah array numerik dan−ascii adalah penspesifikasinya.
Sintaks untuk menggunakan dlmwrite fungsinya adalah -
dlmwrite('my_data.out', num_array, 'dlm_char')dimana, my_data.out adalah file data ASCII yang dipisahkan, num_array adalah array numerik dan dlm_char adalah karakter pembatas.
Contoh
Contoh berikut menunjukkan konsep tersebut. Buat file script dan ketik kode berikut -
num_array = [ 1 2 3 4 ; 4 5 6 7; 7 8 9 0];
save array_data1.out num_array -ascii;
type array_data1.out
dlmwrite('array_data2.out', num_array, ' ');
type array_data2.outSaat Anda menjalankan file, ini akan menampilkan hasil berikut -
1.0000000e+00 2.0000000e+00 3.0000000e+00 4.0000000e+00
4.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00
7.0000000e+00 8.0000000e+00 9.0000000e+00 0.0000000e+00
1 2 3 4
4 5 6 7
7 8 9 0Harap dicatat bahwa perintah save -ascii dan fungsi dlmwrite tidak bekerja dengan array sel sebagai input. Untuk membuat file ASCII yang dipisahkan dari konten array sel, Anda bisa
Baik, konversikan larik sel menjadi matriks menggunakan cell2mat fungsi
Atau ekspor array sel menggunakan fungsi I / O file tingkat rendah.
Jika Anda menggunakan save berfungsi untuk menulis array karakter ke file ASCII, itu menulis ASCII yang setara dengan karakter ke file.
Misalnya, mari kita tulis kata 'halo' ke file -
h = 'hello';
save textdata.out h -ascii
type textdata.outMATLAB menjalankan pernyataan di atas dan menampilkan hasil sebagai berikut. yang merupakan karakter dari string 'hello' dalam format ASCII 8 digit.
1.0400000e+02 1.0100000e+02 1.0800000e+02 1.0800000e+02 1.1100000e+02Menulis ke File Diary
File buku harian adalah log aktivitas sesi MATLAB Anda. Fungsi buku harian membuat salinan persis dari sesi Anda dalam file disk, tidak termasuk grafik.
Untuk mengaktifkan fungsi buku harian, ketik -
diarySecara opsional, Anda dapat memberikan nama file log, misalnya -
diary logdata.outUntuk mematikan fungsi buku harian -
diary offAnda dapat membuka file buku harian di editor teks.
Mengekspor Data ke File Data Teks dengan I / O Tingkat Rendah
Sejauh ini, kami telah mengekspor array numerik. Namun, Anda mungkin perlu membuat file teks lain, termasuk kombinasi data angka dan karakter, file keluaran non-persegi, atau file dengan skema pengkodean non-ASCII. Untuk tujuan ini, MATLAB menyediakan level rendahfprintf fungsi.
Seperti dalam aktivitas file I / O level rendah, sebelum mengekspor, Anda perlu membuka atau membuat file dengan ekstensi fopenberfungsi dan mendapatkan pengenal file. Secara default, fopen membuka file untuk akses read-only. Anda harus menentukan izin untuk menulis atau menambahkan, seperti 'w' atau 'a'.
Setelah memproses file, Anda harus menutupnya dengan fclose(fid) fungsi.
Contoh berikut menunjukkan konsep -
Contoh
Buat file skrip dan ketik kode berikut di dalamnya -
% create a matrix y, with two rows
x = 0:10:100;
y = [x; log(x)];
% open a file for writing
fid = fopen('logtable.txt', 'w');
% Table Header
fprintf(fid, 'Log Function\n\n');
% print values in column order
% two values appear on each row of the file
fprintf(fid, '%f %f\n', y);
fclose(fid);
% display the file created
type logtable.txtSaat Anda menjalankan file, ini akan menampilkan hasil berikut -
Log Function
0.000000 -Inf
10.000000 2.302585
20.000000 2.995732
30.000000 3.401197
40.000000 3.688879
50.000000 3.912023
60.000000 4.094345
70.000000 4.248495
80.000000 4.382027
90.000000 4.499810
100.000000 4.605170Untuk memplot grafik suatu fungsi, Anda perlu mengambil langkah-langkah berikut -
Menetapkan x, dengan menentukan range of values untuk variabel x, yang fungsinya akan diplot
Tentukan fungsinya, y = f(x)
Panggil plot perintah, sebagai plot(x, y)
Contoh berikut akan menunjukkan konsep tersebut. Mari kita gambarkan fungsi sederhananyay = x untuk rentang nilai x dari 0 hingga 100, dengan kenaikan 5.
Buat file script dan ketik kode berikut -
x = [0:5:100];
y = x;
plot(x, y)Saat Anda menjalankan file, MATLAB menampilkan plot berikut -

Mari kita ambil satu contoh lagi untuk memplot fungsi y = x 2 . Dalam contoh ini, kita akan menggambar dua grafik dengan fungsi yang sama, tetapi untuk kedua kalinya, kita akan mengurangi nilai kenaikan. Harap perhatikan bahwa saat kami menurunkan kenaikan, grafik menjadi lebih mulus.
Buat file script dan ketik kode berikut -
x = [1 2 3 4 5 6 7 8 9 10];
x = [-100:20:100];
y = x.^2;
plot(x, y)Saat Anda menjalankan file, MATLAB menampilkan plot berikut -
Ubah file kode sedikit, kurangi kenaikan menjadi 5 -
x = [-100:5:100];
y = x.^2;
plot(x, y)MATLAB menggambar grafik yang lebih halus -
Menambahkan Judul, Label, Garis Kisi dan Skala pada Grafik
MATLAB memungkinkan Anda untuk menambahkan judul, label di sepanjang sumbu x dan sumbu y, garis kisi dan juga untuk menyesuaikan sumbu untuk merapikan grafik.
Itu xlabel dan ylabel perintah menghasilkan label di sepanjang sumbu x dan sumbu y.
Itu title perintah memungkinkan Anda untuk meletakkan judul pada grafik.
Itu grid on perintah memungkinkan Anda untuk meletakkan garis grid pada grafik.
Itu axis equal perintah memungkinkan menghasilkan plot dengan faktor skala yang sama dan spasi pada kedua sumbu.
Itu axis square perintah menghasilkan plot persegi.
Contoh
Buat file script dan ketik kode berikut -
x = [0:0.01:10];
y = sin(x);
plot(x, y), xlabel('x'), ylabel('Sin(x)'), title('Sin(x) Graph'),
grid on, axis equalMATLAB menghasilkan grafik berikut -
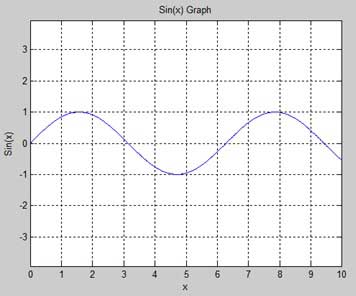
Menggambar Beberapa Fungsi pada Grafik yang Sama
Anda dapat menggambar beberapa grafik pada plot yang sama. Contoh berikut menunjukkan konsep -
Contoh
Buat file script dan ketik kode berikut -
x = [0 : 0.01: 10];
y = sin(x);
g = cos(x);
plot(x, y, x, g, '.-'), legend('Sin(x)', 'Cos(x)')MATLAB menghasilkan grafik berikut -
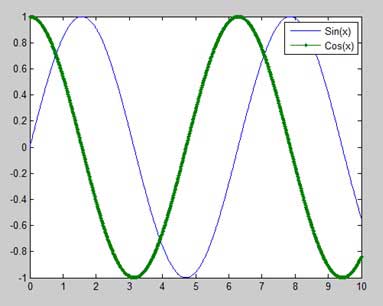
Mengatur Warna pada Grafik
MATLAB menyediakan delapan pilihan warna dasar untuk menggambar grafik. Tabel berikut menunjukkan warna dan kodenya -
| Kode | Warna |
|---|---|
| w | putih |
| k | Hitam |
| b | Biru |
| r | Merah |
| c | Cyan |
| g | hijau |
| m | Magenta |
| y | Kuning |
Contoh
Mari kita gambar grafik dua polinomial
f (x) = 3x 4 + 2x 3 + 7x 2 + 2x + 9 dan
g (x) = 5x 3 + 9x + 2
Buat file script dan ketik kode berikut -
x = [-10 : 0.01: 10];
y = 3*x.^4 + 2 * x.^3 + 7 * x.^2 + 2 * x + 9;
g = 5 * x.^3 + 9 * x + 2;
plot(x, y, 'r', x, g, 'g')Saat Anda menjalankan file, MATLAB menghasilkan grafik berikut -
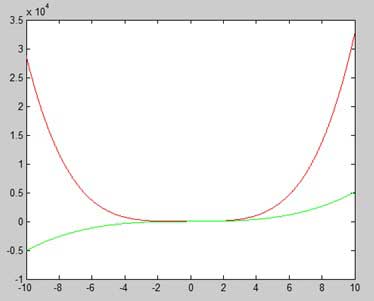
Mengatur Skala Axis
Itu axisperintah memungkinkan Anda untuk mengatur skala sumbu. Anda dapat memberikan nilai minimum dan maksimum untuk sumbu x dan y menggunakan perintah sumbu dengan cara berikut -
axis ( [xmin xmax ymin ymax] )Contoh berikut menunjukkan ini -
Contoh
Buat file script dan ketik kode berikut -
x = [0 : 0.01: 10];
y = exp(-x).* sin(2*x + 3);
plot(x, y), axis([0 10 -1 1])Saat Anda menjalankan file, MATLAB menghasilkan grafik berikut -
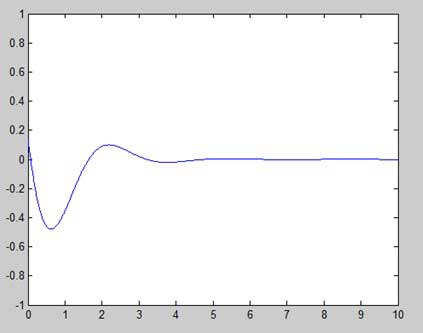
Menghasilkan Sub-Plot
Saat Anda membuat larik plot pada gambar yang sama, masing-masing plot ini disebut subplot. Itusubplot perintah digunakan untuk membuat subplot.
Sintaks untuk perintahnya adalah -
subplot(m, n, p)di mana, m dan n adalah jumlah baris dan kolom dari larik plot dan p menentukan tempat untuk meletakkan plot tertentu.
Setiap plot yang dibuat dengan perintah subplot dapat memiliki karakteristiknya masing-masing. Contoh berikut menunjukkan konsep -
Contoh
Mari kita buat dua plot -
y = e −1,5x sin (10x)
y = e −2x sin (10x)
Buat file script dan ketik kode berikut -
x = [0:0.01:5];
y = exp(-1.5*x).*sin(10*x);
subplot(1,2,1)
plot(x,y), xlabel('x'),ylabel('exp(–1.5x)*sin(10x)'),axis([0 5 -1 1])
y = exp(-2*x).*sin(10*x);
subplot(1,2,2)
plot(x,y),xlabel('x'),ylabel('exp(–2x)*sin(10x)'),axis([0 5 -1 1])Saat Anda menjalankan file, MATLAB menghasilkan grafik berikut -
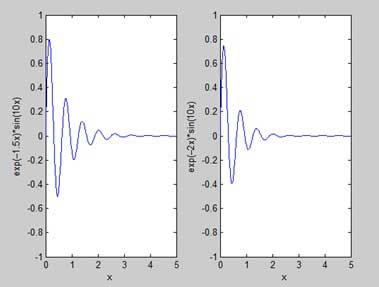
Bab ini akan terus mengeksplorasi kapabilitas plotting dan grafis MATLAB. Kami akan membahas -
- Menggambar diagram batang
- Menggambar kontur
- Plot tiga dimensi
Menggambar Diagram Batang
Itu barperintah menggambar diagram batang dua dimensi. Mari kita ambil contoh untuk mendemonstrasikan idenya.
Contoh
Mari kita buat kelas imajiner dengan 10 siswa. Kita tahu persentase nilai yang diperoleh siswa ini adalah 75, 58, 90, 87, 50, 85, 92, 75, 60, dan 95. Kita akan menggambar diagram batang untuk data ini.
Buat file script dan ketik kode berikut -
x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.epsSaat Anda menjalankan file, MATLAB menampilkan diagram batang berikut -

Menggambar Kontur
Garis kontur dari fungsi dua variabel adalah kurva di mana fungsi tersebut memiliki nilai konstan. Garis kontur digunakan untuk membuat peta kontur dengan menggabungkan titik-titik dengan ketinggian yang sama di atas permukaan tertentu, seperti permukaan laut rata-rata.
MATLAB menyediakan a contour berfungsi untuk menggambar peta kontur.
Contoh
Mari kita buat peta kontur yang menunjukkan garis kontur untuk fungsi tertentu g = f (x, y). Fungsi ini memiliki dua variabel. Jadi, kita harus menghasilkan dua variabel independen, yaitu dua kumpulan data x dan y. Ini dilakukan dengan memanggilmeshgrid perintah.
Itu meshgrid Perintah digunakan untuk menghasilkan matriks elemen yang memberikan rentang x dan y bersama dengan spesifikasi kenaikan dalam setiap kasus.
Mari kita plot fungsi kita g = f (x, y), di mana −5 ≤ x ≤ 5, −3 ≤ y ≤ 3. Mari kita ambil kenaikan 0,1 untuk kedua nilai. Variabel ditetapkan sebagai -
[x,y] = meshgrid(–5:0.1:5, –3:0.1:3);Terakhir, kita perlu menetapkan fungsinya. Misalkan fungsi kita menjadi: x 2 + y 2
Buat file script dan ketik kode berikut -
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables
g = x.^2 + y.^2; % our function
contour(x,y,g) % call the contour function
print -deps graph.epsSaat Anda menjalankan file, MATLAB menampilkan peta kontur berikut -
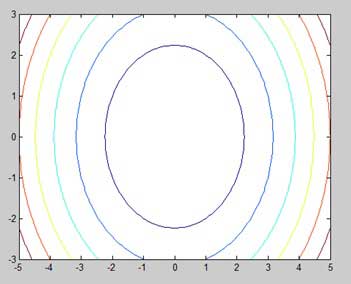
Mari kita ubah sedikit kode untuk mempercantik peta
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables
g = x.^2 + y.^2; % our function
[C, h] = contour(x,y,g); % call the contour function
set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)
print -deps graph.epsSaat Anda menjalankan file, MATLAB menampilkan peta kontur berikut -
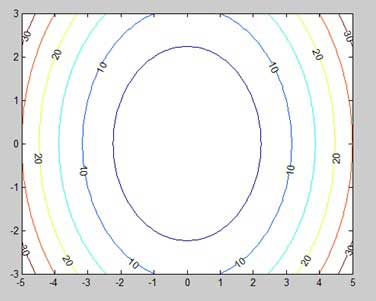
Plot Tiga Dimensi
Plot tiga dimensi pada dasarnya menampilkan permukaan yang ditentukan oleh fungsi dalam dua variabel, g = f (x, y).
Seperti sebelumnya, untuk mendefinisikan g, pertama-tama kita membuat satu set (x, y) poin di atas domain fungsi menggunakan meshgridperintah. Selanjutnya, kami menetapkan fungsinya sendiri. Terakhir, kami menggunakansurf perintah untuk membuat plot permukaan.
Contoh berikut menunjukkan konsep -
Contoh
Mari kita buat peta permukaan 3D untuk fungsi g = xe - (x 2 + y 2 )
Buat file script dan ketik kode berikut -
[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.epsSaat Anda menjalankan file, MATLAB menampilkan peta 3-D berikut -

Anda juga bisa menggunakan meshperintah untuk menghasilkan permukaan tiga dimensi. Namun,surf Perintah menampilkan garis penghubung dan permukaan permukaan dalam warna, sedangkan mesh perintah membuat permukaan wireframe dengan garis berwarna yang menghubungkan titik-titik yang menentukan.
Sejauh ini, kita telah melihat bahwa semua contoh bekerja di MATLAB serta GNU-nya, atau disebut Oktaf. Tetapi untuk menyelesaikan persamaan aljabar dasar, MATLAB dan Oktaf sedikit berbeda, jadi kami akan mencoba untuk membahas MATLAB dan Oktaf di bagian yang terpisah.
Kami juga akan membahas faktorisasi dan penyederhanaan ekspresi aljabar.
Memecahkan Persamaan Aljabar Dasar di MATLAB
Itu solvefungsi digunakan untuk memecahkan persamaan aljabar. Dalam bentuknya yang paling sederhana, fungsi selesaikan menggunakan persamaan yang diapit tanda kutip sebagai argumen.
Misalnya, mari kita selesaikan x dalam persamaan x-5 = 0
solve('x-5=0')MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
5Anda juga dapat memanggil fungsi penyelesaian sebagai -
y = solve('x-5 = 0')MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
y =
5Anda bahkan mungkin tidak memasukkan ruas kanan persamaan -
solve('x-5')MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
5Jika persamaan melibatkan banyak simbol, MATLAB secara default mengasumsikan bahwa Anda sedang menyelesaikan x, namun fungsi penyelesaian memiliki bentuk lain -
solve(equation, variable)dimana, Anda juga bisa menyebutkan variabelnya.
Sebagai contoh, mari kita selesaikan persamaan v - u - 3t 2 = 0, untuk v. Dalam kasus ini, kita harus menulis -
solve('v-u-3*t^2=0', 'v')MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
3*t^2 + uMemecahkan Persamaan Aljabar Dasar dalam Oktaf
Itu roots fungsi digunakan untuk menyelesaikan persamaan aljabar dalam Oktaf dan Anda dapat menulis contoh di atas sebagai berikut -
Misalnya, mari kita selesaikan x dalam persamaan x-5 = 0
roots([1, -5])Oktaf akan mengeksekusi pernyataan di atas dan mengembalikan hasil berikut -
ans = 5Anda juga dapat memanggil fungsi penyelesaian sebagai -
y = roots([1, -5])Oktaf akan mengeksekusi pernyataan di atas dan mengembalikan hasil berikut -
y = 5Memecahkan Persamaan Kuadrat di MATLAB
Itu solvefungsi juga dapat memecahkan persamaan orde tinggi. Ini sering digunakan untuk menyelesaikan persamaan kuadrat. Fungsi mengembalikan akar persamaan dalam larik.
Contoh berikut menyelesaikan persamaan kuadrat x 2 -7x +12 = 0. Buat file script dan ketikkan kode berikut -
eq = 'x^2 -7*x + 12 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
The first root is:
3
The second root is:
4Memecahkan Persamaan Kuadrat dalam Oktaf
Contoh berikut menyelesaikan persamaan kuadrat x 2 -7x +12 = 0 dalam Oktaf. Buat file script dan ketik kode berikut -
s = roots([1, -7, 12]);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
The first root is:
4
The second root is:
3Memecahkan Persamaan Orde Tinggi di MATLAB
Itu solvefungsi juga dapat memecahkan persamaan orde tinggi. Sebagai contoh, mari kita selesaikan persamaan kubik sebagai (x-3) 2 (x-7) = 0
solve('(x-3)^2*(x-7)=0')MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
3
3
7Dalam kasus persamaan orde tinggi, akar panjang mengandung banyak suku. Anda bisa mendapatkan nilai numerik dari akar tersebut dengan mengubahnya menjadi dua kali lipat. Contoh berikut menyelesaikan persamaan orde empat x 4 - 7x 3 + 3x 2 - 5x + 9 = 0.
Buat file script dan ketik kode berikut -
eq = 'x^4 - 7*x^3 + 3*x^2 - 5*x + 9 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));
disp('The third root is: '), disp(s(3));
disp('The fourth root is: '), disp(s(4));
% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));Saat Anda menjalankan file, ia mengembalikan hasil berikut -
The first root is:
6.630396332390718431485053218985
The second root is:
1.0597804633025896291682772499885
The third root is:
- 0.34508839784665403032666523448675 - 1.0778362954630176596831109269793*i
The fourth root is:
- 0.34508839784665403032666523448675 + 1.0778362954630176596831109269793*i
Numeric value of first root
6.6304
Numeric value of second root
1.0598
Numeric value of third root
-0.3451 - 1.0778i
Numeric value of fourth root
-0.3451 + 1.0778iHarap diperhatikan bahwa dua akar terakhir adalah bilangan kompleks.
Memecahkan Persamaan Orde Tinggi dalam Oktaf
Contoh berikut menyelesaikan persamaan orde empat x 4 - 7x 3 + 3x 2 - 5x + 9 = 0.
Buat file script dan ketik kode berikut -
v = [1, -7, 3, -5, 9];
s = roots(v);
% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));Saat Anda menjalankan file, ia mengembalikan hasil berikut -
Numeric value of first root
6.6304
Numeric value of second root
-0.34509 + 1.07784i
Numeric value of third root
-0.34509 - 1.07784i
Numeric value of fourth root
1.0598Menyelesaikan Sistem Persamaan di MATLAB
Itu solvefungsi juga dapat digunakan untuk menghasilkan solusi sistem persamaan yang melibatkan lebih dari satu variabel. Mari kita ambil contoh sederhana untuk mendemonstrasikan penggunaan ini.
Mari kita selesaikan persamaan -
5x + 9y = 5
3x - 6y = 4
Buat file script dan ketik kode berikut -
s = solve('5*x + 9*y = 5','3*x - 6*y = 4');
s.x
s.ySaat Anda menjalankan file, ini akan menampilkan hasil berikut -
ans =
22/19
ans =
-5/57Dengan cara yang sama, Anda dapat menyelesaikan sistem linier yang lebih besar. Pertimbangkan kumpulan persamaan berikut -
x + 3y -2z = 5
3x + 5y + 6z = 7
2x + 4y + 3z = 8
Menyelesaikan Sistem Persamaan dalam Oktaf
Kami memiliki pendekatan yang sedikit berbeda untuk menyelesaikan sistem persamaan linier 'n' dalam 'n' yang tidak diketahui. Mari kita ambil contoh sederhana untuk mendemonstrasikan penggunaan ini.
Mari kita selesaikan persamaan -
5x + 9y = 5
3x - 6y = 4
Sistem persamaan linier seperti itu dapat dituliskan sebagai persamaan matriks tunggal Ax = b, di mana A adalah matriks koefisien, b adalah vektor kolom yang berisi ruas kanan persamaan linier dan x adalah vektor kolom yang mewakili solusi sebagai ditampilkan pada program di bawah ini -
Buat file script dan ketik kode berikut -
A = [5, 9; 3, -6];
b = [5;4];
A \ bSaat Anda menjalankan file, ini akan menampilkan hasil berikut -
ans =
1.157895
-0.087719Dengan cara yang sama, Anda dapat menyelesaikan sistem linier yang lebih besar seperti yang diberikan di bawah ini -
x + 3y -2z = 5
3x + 5y + 6z = 7
2x + 4y + 3z = 8
Memperluas dan Mengumpulkan Persamaan di MATLAB
Itu expand dan collectfungsi memperluas dan mengumpulkan persamaan masing-masing. Contoh berikut menunjukkan konsep -
Ketika Anda bekerja dengan banyak fungsi simbolik, Anda harus menyatakan bahwa variabel Anda adalah simbolik.
Buat file script dan ketik kode berikut -
syms x %symbolic variable x
syms y %symbolic variable x
% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(sin(2*x))
expand(cos(x+y))
% collecting equations
collect(x^3 *(x-7))
collect(x^4*(x-3)*(x-5))Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
ans =
x^2 + 4*x - 45
ans =
x^4 + x^3 - 43*x^2 + 23*x + 210
ans =
2*cos(x)*sin(x)
ans =
cos(x)*cos(y) - sin(x)*sin(y)
ans =
x^4 - 7*x^3
ans =
x^6 - 8*x^5 + 15*x^4Memperluas dan Mengumpulkan Persamaan dalam Oktaf
Anda harus memiliki symbolic paket, yang menyediakan expand dan collectberfungsi untuk memperluas dan mengumpulkan persamaan. Contoh berikut menunjukkan konsep -
Saat Anda bekerja dengan banyak fungsi simbolik, Anda harus menyatakan bahwa variabel Anda simbolis tetapi Oktaf memiliki pendekatan yang berbeda untuk mendefinisikan variabel simbolik. Perhatikan penggunaanSin dan Cos, yang juga didefinisikan dalam paket simbolik.
Buat file script dan ketik kode berikut -
% first of all load the package, make sure its installed.
pkg load symbolic
% make symbols module available
symbols
% define symbolic variables
x = sym ('x');
y = sym ('y');
z = sym ('z');
% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(Sin(2*x))
expand(Cos(x+y))
% collecting equations
collect(x^3 *(x-7), z)
collect(x^4*(x-3)*(x-5), z)Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
ans =
-45.0+x^2+(4.0)*x
ans =
210.0+x^4-(43.0)*x^2+x^3+(23.0)*x
ans =
sin((2.0)*x)
ans =
cos(y+x)
ans =
x^(3.0)*(-7.0+x)
ans =
(-3.0+x)*x^(4.0)*(-5.0+x)Faktorisasi dan Penyederhanaan Ekspresi Aljabar
Itu factor fungsi memfaktorkan ekspresi dan simplifyfungsi menyederhanakan ekspresi. Contoh berikut menunjukkan konsep -
Contoh
Buat file script dan ketik kode berikut -
syms x
syms y
factor(x^3 - y^3)
factor([x^2-y^2,x^3+y^3])
simplify((x^4-16)/(x^2-4))Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
ans =
(x - y)*(x^2 + x*y + y^2)
ans =
[ (x - y)*(x + y), (x + y)*(x^2 - x*y + y^2)]
ans =
x^2 + 4MATLAB menyediakan berbagai cara untuk memecahkan masalah diferensial dan kalkulus integral, menyelesaikan persamaan diferensial dari berbagai derajat dan perhitungan batas. Yang terbaik dari semuanya, Anda dapat dengan mudah memplot grafik fungsi kompleks dan memeriksa titik maksimum, minimum, dan alat tulis lainnya pada grafik dengan menyelesaikan fungsi asli, serta turunannya.
Bab ini akan membahas masalah kalkulus. Pada bab ini, kita akan membahas konsep pra-kalkulus, yaitu menghitung batas fungsi dan memverifikasi sifat batas.
Dalam Diferensial bab berikutnya , kita akan menghitung turunan dari sebuah ekspresi dan menemukan maksima dan minima lokal pada grafik. Kami juga akan membahas penyelesaian persamaan diferensial.
Terakhir, pada bab Integrasi , kita akan membahas kalkulus integral.
Menghitung Batas
MATLAB menyediakan limitberfungsi untuk menghitung batas. Dalam bentuknya yang paling dasar, filelimit function mengambil ekspresi sebagai argumen dan menemukan batas ekspresi sebagai variabel independen menuju nol.
Sebagai contoh, mari kita hitung limit dari sebuah fungsi f (x) = (x 3 + 5) / (x 4 + 7), karena x cenderung nol.
syms x
limit((x^3 + 5)/(x^4 + 7))MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
5/7Fungsi batas termasuk dalam bidang komputasi simbolik; Anda perlu menggunakansymsberfungsi untuk memberi tahu MATLAB variabel simbolik mana yang Anda gunakan. Anda juga dapat menghitung batas suatu fungsi, karena variabel cenderung ke beberapa angka selain nol. Untuk menghitung lim x-> a (f (x)), kami menggunakan perintah limit dengan argumen. Yang pertama adalah ekspresi dan yang kedua adalah angka, yang didekati x , ini dia a .
Sebagai contoh, mari kita hitung limit dari sebuah fungsi f (x) = (x-3) / (x-1), karena x cenderung 1.
limit((x - 3)/(x-1),1)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
NaNMari kita ambil contoh lain,
limit(x^2 + 5, 3)MATLAB akan mengeksekusi pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
14Menghitung Batas menggunakan Oktaf
Berikut ini adalah versi Oktaf dari contoh di atas menggunakan symbolic paket, coba jalankan dan bandingkan hasilnya -
pkg load symbolic
symbols
x = sym("x");
subs((x^3+5)/(x^4+7),x,0)Oktaf akan mengeksekusi pernyataan di atas dan mengembalikan hasil berikut -
ans =
0.7142857142857142857Verifikasi Sifat Dasar Batasan
Teorema Batas Aljabar memberikan beberapa sifat dasar batas. Ini adalah sebagai berikut -
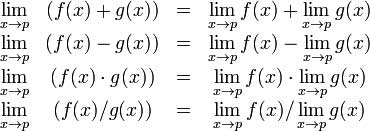
Mari kita pertimbangkan dua fungsi -
- f (x) = (3x + 5) / (x - 3)
- g (x) = x 2 + 1.
Mari kita hitung batas fungsi karena x cenderung 5, dari kedua fungsi dan memverifikasi sifat dasar batas menggunakan dua fungsi dan MATLAB.
Contoh
Buat file skrip dan ketikkan kode berikut ke dalamnya -
syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)Saat Anda menjalankan file, ini akan menampilkan -
l1 =
17
l2 =
17
lAdd =
34
lSub =
0
lMult =
289
lDiv =
1Verifikasi Properti Dasar Batas menggunakan Oktaf
Berikut ini adalah versi Oktaf dari contoh di atas menggunakan symbolic paket, coba jalankan dan bandingkan hasilnya -
pkg load symbolic
symbols
x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)Oktaf akan mengeksekusi pernyataan di atas dan mengembalikan hasil berikut -
l1 =
17.0
l2 =
17.0
lAdd =
34.0
lSub =
0.0
lMult =
289.0
lDiv =
1.0Batas Sisi Kiri dan Kanan
Ketika suatu fungsi memiliki diskontinuitas untuk beberapa nilai variabel tertentu, batasnya tidak ada pada titik itu. Dengan kata lain, limit dari sebuah fungsi f (x) memiliki diskontinuitas pada x = a, ketika nilai limit, ketika x mendekati x dari sisi kiri, tidak sama dengan nilai limit ketika x mendekati dari sisi kanan.
Ini mengarah pada konsep batas tangan kiri dan tangan kanan. Batas tangan kiri didefinisikan sebagai batas sebagai x -> a, dari kiri, yaitu x mendekati a, untuk nilai x <a. Batas tangan kanan didefinisikan sebagai batas sebagai x -> a, dari kanan, yaitu x mendekati a, untuk nilai x> a. Ketika batas tangan kiri dan batas tangan kanan tidak sama, batas itu tidak ada.
Mari kita pertimbangkan fungsi -
f(x) = (x - 3)/|x - 3|
Kami akan menunjukkan bahwa lim x-> 3 f (x) tidak ada. MATLAB membantu kami menetapkan fakta ini dengan dua cara -
- Dengan memplot grafik fungsi dan menunjukkan diskontinuitas.
- Dengan menghitung batas dan menunjukkan bahwa keduanya berbeda.
Batas tangan kiri dan tangan kanan dihitung dengan meneruskan string karakter 'kiri' dan 'kanan' ke perintah limit sebagai argumen terakhir.
Contoh
Buat file skrip dan ketikkan kode berikut ke dalamnya -
f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')Saat Anda menjalankan file, MATLAB menggambar plot berikut
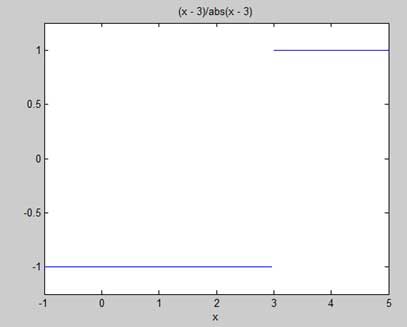
Setelah output berikut ini ditampilkan -
l =
-1
r =
1MATLAB menyediakan diffperintah untuk menghitung turunan simbolik. Dalam bentuknya yang paling sederhana, Anda meneruskan fungsi yang ingin Anda bedakan ke perintah diff sebagai argumen.
Sebagai contoh, mari kita hitung turunan dari fungsi f (t) = 3t 2 + 2t -2
Contoh
Buat file skrip dan ketikkan kode berikut ke dalamnya -
syms t
f = 3*t^2 + 2*t^(-2);
diff(f)Ketika kode di atas dikompilasi dan dijalankan, itu menghasilkan hasil sebagai berikut -
ans =
6*t - 4/t^3Berikut adalah Oktaf yang setara dengan perhitungan di atas -
pkg load symbolic
symbols
t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)Oktaf mengeksekusi kode dan mengembalikan hasil berikut -
ans =
-(4.0)*t^(-3.0)+(6.0)*tVerifikasi Aturan Dasar Diferensiasi
Mari kita nyatakan secara singkat berbagai persamaan atau aturan untuk diferensiasi fungsi dan verifikasi aturan ini. Untuk tujuan ini, kita akan menulis f '(x) untuk turunan orde pertama dan f "(x) untuk turunan orde dua.
Berikut adalah aturan untuk diferensiasi -
Aturan 1
Untuk setiap fungsi f dan g dan bilangan real a dan b adalah turunan dari fungsi -
h(x) = af(x) + bg(x) sehubungan dengan x diberikan oleh -
h'(x) = af'(x) + bg'(x)
Aturan 2
Itu sum dan subtraction aturan menyatakan bahwa jika f dan g adalah dua fungsi, f 'dan g' adalah turunannya masing-masing, maka,
(f + g)' = f' + g'
(f - g)' = f' - g'
Aturan 3
Itu product Aturan menyatakan bahwa jika f dan g adalah dua fungsi, f 'dan g' adalah turunannya masing-masing, maka,
(f.g)' = f'.g + g'.f
Aturan 4
Itu quotient Aturan menyatakan bahwa jika f dan g adalah dua fungsi, f 'dan g' adalah turunannya masing-masing, maka,
(f/g)' = (f'.g - g'.f)/g2
Aturan 5
Itu polynomial atau aturan pangkat dasar menyatakan bahwa, jika y = f(x) = xn, kemudian f' = n. x(n-1)
Hasil langsung dari aturan ini adalah turunan dari setiap konstanta adalah nol, yaitu jika y = k, konstanta apa pun, lalu
f' = 0
Aturan 6
Itu chain aturan menyatakan bahwa, turunan dari fungsi suatu fungsi h(x) = f(g(x)) sehubungan dengan x adalah,
h'(x)= f'(g(x)).g'(x)
Contoh
Buat file skrip dan ketikkan kode berikut ke dalamnya -
syms x
syms t
f = (x + 2)*(x^2 + 3)
der1 = diff(f)
f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)
f = (x^2 + 1)^17
der5 = diff(f)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)Saat Anda menjalankan file, MATLAB menampilkan hasil berikut -
f =
(x^2 + 3)*(x + 2)
der1 =
2*x*(x + 2) + x^2 + 3
f =
(t^(1/2) + t^3)*(t^2 + 3)
der2 =
(t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
f =
(x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 =
(2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
f =
(2*x^2 + 3*x)/(x^3 + 1)
der4 =
(4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
f =
(x^2 + 1)^17
der5 =
34*x*(x^2 + 1)^16
f =
1/(t^3 + 3*t^2 + 5*t - 9)^6
der6 =
-(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7Berikut adalah Oktaf yang setara dengan perhitungan di atas -
pkg load symbolic
symbols
x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3)
der1 = differentiate(f,x)
f = (t^2 + 3)*(t^(1/2) + t^3)
der2 = differentiate(f,t)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = differentiate(f,x)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = differentiate(f,x)
f = (x^2 + 1)^17
der5 = differentiate(f,x)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = differentiate(f,t)Oktaf mengeksekusi kode dan mengembalikan hasil berikut -
f =
(2.0+x)*(3.0+x^(2.0))
der1 =
3.0+x^(2.0)+(2.0)*(2.0+x)*x
f =
(t^(3.0)+sqrt(t))*(3.0+t^(2.0))
der2 =
(2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0))
f =
(1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))
der3 =
(-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x)
f =
(1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x)
der4 =
(1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x)
f =
(1.0+x^(2.0))^(17.0)
der5 =
(34.0)*(1.0+x^(2.0))^(16.0)*x
f =
(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0)
der6 =
-(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)Turunan dari Fungsi Eksponensial, Logaritmik dan Trigonometri
Tabel berikut menyediakan turunan dari fungsi eksponensial, logaritmik dan trigonometri yang umum digunakan -
| Fungsi | Turunan |
|---|---|
| ca.x | c a.x .ln ca (ln adalah logaritma natural) |
| ex | e x |
| ln x | 1 / x |
| lncx | 1 / x.ln c |
| xx | x x . (1 + ln x) |
| sin(x) | cos (x) |
| cos(x) | -sin (x) |
| tan(x) | sec 2 (x), atau 1 / cos 2 (x), atau 1 + tan 2 (x) |
| cot(x) | -csc 2 (x), atau -1 / sin 2 (x), atau - (1 + cot 2 (x)) |
| sec(x) | dtk (x) .tan (x) |
| csc(x) | -csc (x) .cot (x) |
Contoh
Buat file skrip dan ketikkan kode berikut ke dalamnya -
syms x
y = exp(x)
diff(y)
y = x^9
diff(y)
y = sin(x)
diff(y)
y = tan(x)
diff(y)
y = cos(x)
diff(y)
y = log(x)
diff(y)
y = log10(x)
diff(y)
y = sin(x)^2
diff(y)
y = cos(3*x^2 + 2*x + 1)
diff(y)
y = exp(x)/sin(x)
diff(y)Saat Anda menjalankan file, MATLAB menampilkan hasil berikut -
y =
exp(x)
ans =
exp(x)
y =
x^9
ans =
9*x^8
y =
sin(x)
ans =
cos(x)
y =
tan(x)
ans =
tan(x)^2 + 1
y =
cos(x)
ans =
-sin(x)
y =
log(x)
ans =
1/x
y =
log(x)/log(10)
ans =
1/(x*log(10))
y =
sin(x)^2
ans =
2*cos(x)*sin(x)
y =
cos(3*x^2 + 2*x + 1)
ans =
-sin(3*x^2 + 2*x + 1)*(6*x + 2)
y =
exp(x)/sin(x)
ans =
exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2Berikut adalah Oktaf yang setara dengan perhitungan di atas -
pkg load symbolic
symbols
x = sym("x");
y = Exp(x)
differentiate(y,x)
y = x^9
differentiate(y,x)
y = Sin(x)
differentiate(y,x)
y = Tan(x)
differentiate(y,x)
y = Cos(x)
differentiate(y,x)
y = Log(x)
differentiate(y,x)
% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)
y = Sin(x)^2
differentiate(y,x)
y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)
y = Exp(x)/Sin(x)
differentiate(y,x)Oktaf mengeksekusi kode dan mengembalikan hasil berikut -
y =
exp(x)
ans =
exp(x)
y =
x^(9.0)
ans =
(9.0)*x^(8.0)
y =
sin(x)
ans =
cos(x)
y =
tan(x)
ans =
1+tan(x)^2
y =
cos(x)
ans =
-sin(x)
y =
log(x)
ans =
x^(-1)
y =
sin(x)^(2.0)
ans =
(2.0)*sin(x)*cos(x)
y =
cos(1.0+(2.0)*x+(3.0)*x^(2.0))
ans =
-(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0))
y =
sin(x)^(-1)*exp(x)
ans =
sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)Menghitung Derivatif Tingkat Tinggi
Untuk menghitung turunan yang lebih tinggi dari fungsi f, kita menggunakan sintaks diff(f,n).
Mari kita hitung turunan kedua dari fungsi y = f (x) = x .e -3x
f = x*exp(-3*x);
diff(f, 2)MATLAB menjalankan kode dan mengembalikan hasil berikut -
ans =
9*x*exp(-3*x) - 6*exp(-3*x)Berikut adalah Oktaf yang setara dengan perhitungan di atas -
pkg load symbolic
symbols
x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)Oktaf mengeksekusi kode dan mengembalikan hasil berikut -
ans =
(9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)Contoh
Dalam contoh ini, mari kita pecahkan masalah. Mengingat bahwa sebuah fungsiy = f(x) = 3 sin(x) + 7 cos(5x). Kita harus mencari tahu apakah persamaannyaf" + f = -5cos(2x) benar.
Buat file skrip dan ketikkan kode berikut ke dalamnya -
syms x
y = 3*sin(x)+7*cos(5*x); % defining the function
lhs = diff(y,2)+y; %evaluting the lhs of the equation
rhs = -5*cos(2*x); %rhs of the equation
if(isequal(lhs,rhs))
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
No, the equation does not hold true
Value of LHS is:
-168*cos(5*x)Berikut adalah Oktaf yang setara dengan perhitungan di atas -
pkg load symbolic
symbols
x = sym("x");
y = 3*Sin(x)+7*Cos(5*x); % defining the function
lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation
rhs = -5*Cos(2*x); %rhs of the equation
if(lhs == rhs)
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);Oktaf mengeksekusi kode dan mengembalikan hasil berikut -
No, the equation does not hold true
Value of LHS is:
-(168.0)*cos((5.0)*x)Menemukan Maxima dan Minima dari sebuah Kurva
Jika kita mencari nilai maksimum dan minimum lokal untuk sebuah grafik, pada dasarnya kita mencari titik tertinggi atau terendah pada grafik fungsi di lokasi tertentu, atau untuk rentang nilai tertentu dari variabel simbolik.
Untuk fungsi y = f (x) titik-titik pada grafik di mana grafik memiliki kemiringan nol disebut stationary points. Dengan kata lain, titik stasioner adalah di mana f '(x) = 0.
Untuk mencari titik stasioner dari suatu fungsi yang kita turunkan, kita perlu menetapkan turunannya sama dengan nol dan menyelesaikan persamaannya.
Contoh
Mari kita cari titik stasioner dari fungsi f (x) = 2x 3 + 3x 2 - 12x + 17
Lakukan langkah-langkah berikut -
First let us enter the function and plot its graph.
syms x
y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function
ezplot(y)MATLAB menjalankan kode dan mengembalikan plot berikut -
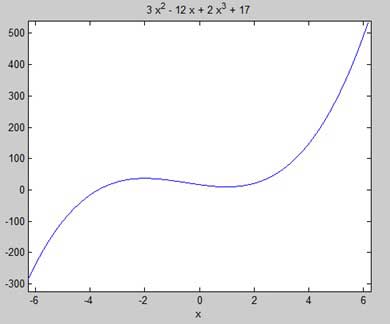
Berikut adalah kode setara Oktaf untuk contoh di atas -
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y)
print -deps graph.epsOur aim is to find some local maxima and minima on the graph, so let us find the local maxima and minima for the interval [-2, 2] on the graph.
syms x
y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function
ezplot(y, [-2, 2])MATLAB menjalankan kode dan mengembalikan plot berikut -
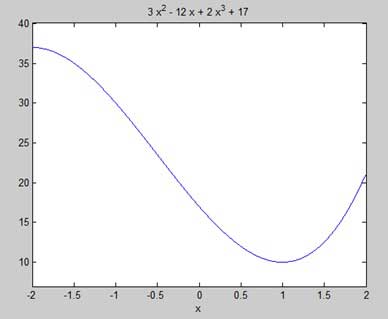
Berikut adalah kode setara Oktaf untuk contoh di atas -
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y, [-2, 2])
print -deps graph.epsNext, let us compute the derivative.
g = diff(y)MATLAB menjalankan kode dan mengembalikan hasil berikut -
g =
6*x^2 + 6*x - 12Berikut adalah Oktaf yang setara dari perhitungan di atas -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)Oktaf mengeksekusi kode dan mengembalikan hasil berikut -
g =
-12.0+(6.0)*x+(6.0)*x^(2.0)Let us solve the derivative function, g, to get the values where it becomes zero.
s = solve(g)MATLAB menjalankan kode dan mengembalikan hasil berikut -
s =
1
-2Berikut adalah Oktaf yang setara dengan perhitungan di atas -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])Oktaf mengeksekusi kode dan mengembalikan hasil berikut -
g =
-12.0+(6.0)*x^(2.0)+(6.0)*x
ans =
-2
1This agrees with our plot. So let us evaluate the function f at the critical points x = 1, -2. Kita dapat mengganti nilai dalam fungsi simbolik dengan menggunakan subs perintah.
subs(y, 1), subs(y, -2)MATLAB menjalankan kode dan mengembalikan hasil berikut -
ans =
10
ans =
37Berikut adalah Oktaf yang setara dengan perhitungan di atas -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)ans =
10.0
ans =
37.0-4.6734207789940138748E-18*IOleh karena itu, nilai minimum dan maksimum pada fungsi f (x) = 2x 3 + 3x 2 - 12x + 17, pada interval [-2,2] adalah 10 dan 37.
Memecahkan Persamaan Diferensial
MATLAB menyediakan dsolve perintah untuk menyelesaikan persamaan diferensial secara simbolis.
Bentuk paling dasar dari file dsolve perintah untuk mencari solusi persamaan tunggal adalah
dsolve('eqn')dimana eqn adalah string teks yang digunakan untuk memasukkan persamaan.
Ini mengembalikan solusi simbolis dengan satu set konstanta arbitrer yang MATLAB beri label C1, C2, dan seterusnya.
Anda juga dapat menentukan kondisi awal dan batas untuk masalah tersebut, sebagai daftar yang dipisahkan koma mengikuti persamaan sebagai -
dsolve('eqn','cond1', 'cond2',…)Untuk tujuan menggunakan perintah dsolve, derivatives are indicated with a D. Misalnya, persamaan seperti f '(t) = -2 * f + biaya (t) dimasukkan sebagai -
'Df = -2*f + cos(t)'
Turunan yang lebih tinggi ditunjukkan dengan mengikuti D dengan urutan turunannya.
Misalnya persamaan f "(x) + 2f '(x) = 5sin3x harus dimasukkan sebagai -
'D2y + 2Dy = 5*sin(3*x)'
Mari kita ambil contoh sederhana dari persamaan diferensial orde satu: y '= 5y.
s = dsolve('Dy = 5*y')MATLAB menjalankan kode dan mengembalikan hasil berikut -
s =
C2*exp(5*t)Mari kita ambil contoh lain dari persamaan diferensial orde dua sebagai: y "- y = 0, y (0) = -1, y '(0) = 2.
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')MATLAB menjalankan kode dan mengembalikan hasil berikut -
ans =
exp(t)/2 - (3*exp(-t))/2Integrasi berhubungan dengan dua jenis masalah yang pada dasarnya berbeda.
Pada tipe pertama, turunan dari suatu fungsi diberikan dan kita ingin mencari fungsinya. Oleh karena itu, pada dasarnya kami membalik proses diferensiasi. Proses kebalikan ini dikenal sebagai anti-diferensiasi, atau menemukan fungsi primitif, atau menemukanindefinite integral.
Jenis masalah kedua melibatkan penjumlahan sejumlah besar kuantitas yang sangat kecil dan kemudian mengambil batas ketika ukuran kuantitas mendekati nol, sedangkan jumlah suku cenderung tak terhingga. Proses ini mengarah pada definisi filedefinite integral.
Integral pasti digunakan untuk mencari luas, volume, pusat gravitasi, momen inersia, pekerjaan yang dilakukan oleh suatu gaya, dan dalam berbagai aplikasi lainnya.
Menemukan Integral Tak Terbatas Menggunakan MATLAB
Menurut definisi, jika turunan dari fungsi f (x) adalah f '(x), maka kita katakan bahwa integral tak tentu dari f' (x) terhadap x adalah f (x). Misalnya, karena turunan (terhadap x) dari x 2 adalah 2x, kita dapat mengatakan bahwa integral tak tentu dari 2x adalah x 2 .
Dalam simbol -
f'(x2) = 2x, oleh karena itu,
∫ 2xdx = x2.
Integral tak tentu tidak unik, karena turunan dari x 2 + c, untuk nilai konstanta c apa pun, juga akan menjadi 2x.
Ini diekspresikan dalam simbol sebagai -
∫ 2xdx = x2 + c.
Dimana, c disebut sebagai 'konstanta sembarang'.
MATLAB menyediakan file intperintah untuk menghitung integral dari ekspresi. Untuk mendapatkan ekspresi integral tak tentu dari suatu fungsi, kita menulis -
int(f);Misalnya, dari contoh kami sebelumnya -
syms x
int(2*x)MATLAB menjalankan pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
x^2Contoh 1
Dalam contoh ini, mari kita temukan integral dari beberapa ekspresi yang umum digunakan. Buat file skrip dan ketik kode berikut di dalamnya -
syms x n
int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
ans =
piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
-cos(n*t)/n
ans =
(a*sin(pi*t))/pi
ans =
a^x/log(a)Contoh 2
Buat file skrip dan ketik kode berikut di dalamnya -
syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))
int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))
int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))Perhatikan bahwa file pretty fungsi mengembalikan ekspresi dalam format yang lebih mudah dibaca.
Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
ans =
sin(x)
ans =
exp(x)
ans =
x*(log(x) - 1)
ans =
log(x)
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
2 4
24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x)
----------- + ------------- - -------------- + ------------
3125 625 125 5
3 5
4 x sin(5 x) x sin(5 x)
------------- + -----------
25 5
ans =
-1/(4*x^4)
ans =
tan(x)
2
x (3 x - 5 x + 1)
ans =
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
6 5 4 3
7 x 3 x 5 x x
- ---- - ---- + ---- + --
12 5 8 2Menemukan Integral Pasti Menggunakan MATLAB
Menurut definisi, integral pasti pada dasarnya adalah batas penjumlahan. Kami menggunakan integral pasti untuk mencari area seperti area antara kurva dan sumbu x dan area antara dua kurva. Integral pasti juga dapat digunakan dalam situasi lain, di mana kuantitas yang dibutuhkan dapat dinyatakan sebagai batas penjumlahan.
Itu int fungsi dapat digunakan untuk integrasi tertentu dengan melewati batas yang ingin Anda hitung integralnya.
Menghitung
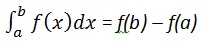
kami menulis,
int(x, a, b)Misalnya, untuk menghitung nilai yang

int(x, 4, 9)MATLAB menjalankan pernyataan di atas dan mengembalikan hasil sebagai berikut -
ans =
65/2Berikut adalah Oktaf yang setara dengan perhitungan di atas -
pkg load symbolic
symbols
x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);
a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));Oktaf mengeksekusi kode dan mengembalikan hasil berikut -
Area:
32.500Solusi alternatif dapat diberikan menggunakan fungsi quad () yang disediakan oleh Oktaf sebagai berikut -
pkg load symbolic
symbols
f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);
display('Area: '), disp(double(a));Oktaf mengeksekusi kode dan mengembalikan hasil berikut -
Area:
32.500Contoh 1
Mari kita hitung luas area antara sumbu x, dan kurva y = x 3 −2x + 5 serta ordinatnya x = 1 dan x = 2.
Area yang dibutuhkan diberikan oleh -
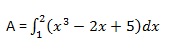
Buat file script dan ketik kode berikut -
f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
a =
23/4
Area:
5.7500Berikut adalah Oktaf yang setara dengan perhitungan di atas -
pkg load symbolic
symbols
x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);
a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));Oktaf mengeksekusi kode dan mengembalikan hasil berikut -
Area:
5.7500Solusi alternatif dapat diberikan menggunakan fungsi quad () yang disediakan oleh Oktaf sebagai berikut -
pkg load symbolic
symbols
x = sym("x");
f = inline("x^3 - 2*x +5");
[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));Oktaf mengeksekusi kode dan mengembalikan hasil berikut -
Area:
5.7500Contoh 2
Temukan luas di bawah kurva: f (x) = x 2 cos (x) untuk −4 ≤ x ≤ 9.
Buat file script dan tulis kode berikut -
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));Saat Anda menjalankan file, MATLAB memplot grafik -
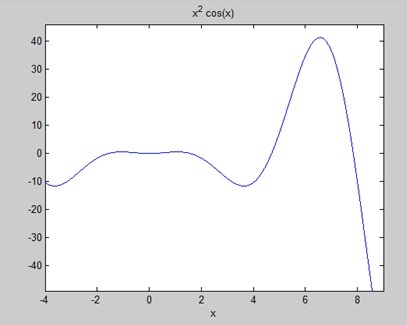
Outputnya diberikan di bawah ini -
a =
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
Area:
0.3326Berikut adalah Oktaf yang setara dengan perhitungan di atas -
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));MATLAB merepresentasikan polinomial sebagai vektor baris yang berisi koefisien yang diurutkan berdasarkan pangkat turun. Misalnya, persamaan P (x) = x 4 + 7x 3 - 5x + 9 dapat direpresentasikan sebagai -
p = [1 7 0 -5 9];
Mengevaluasi Polinomial
Itu polyvalfungsi digunakan untuk mengevaluasi polinomial pada nilai yang ditentukan. Misalnya, untuk mengevaluasi polinomial kita sebelumnyap, pada x = 4, ketik -
p = [1 7 0 -5 9];
polyval(p,4)MATLAB menjalankan pernyataan di atas dan mengembalikan hasil berikut -
ans = 693MATLAB juga menyediakan file polyvalmberfungsi untuk mengevaluasi matriks polinomial. Polinomial matriks adalah apolynomial dengan matriks sebagai variabel.
Sebagai contoh, mari kita membuat matriks persegi X dan mengevaluasi polinom p, di X -
p = [1 7 0 -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)MATLAB menjalankan pernyataan di atas dan mengembalikan hasil berikut -
ans =
2307 -1769 -939 4499
2314 -2376 -249 4695
2256 -1892 -549 4310
4570 -4532 -1062 9269Menemukan Akar Polinomial
Itu rootsfungsi menghitung akar polinomial. Misalnya, untuk menghitung akar dari polinom p kita, ketik -
p = [1 7 0 -5 9];
r = roots(p)MATLAB menjalankan pernyataan di atas dan mengembalikan hasil berikut -
r =
-6.8661 + 0.0000i
-1.4247 + 0.0000i
0.6454 + 0.7095i
0.6454 - 0.7095iFungsinya polyadalah kebalikan dari fungsi akar dan kembali ke koefisien polinomial. Misalnya -
p2 = poly(r)MATLAB menjalankan pernyataan di atas dan mengembalikan hasil berikut -
p2 =
Columns 1 through 3:
1.00000 + 0.00000i 7.00000 + 0.00000i 0.00000 + 0.00000i
Columns 4 and 5:
-5.00000 - 0.00000i 9.00000 + 0.00000iPemasangan Kurva Polinomial
Itu polyfitfungsi menemukan koefisien polinomial yang sesuai dengan sekumpulan data dalam arti kuadrat-terkecil. Jika x dan y adalah dua vektor yang berisi data x dan y untuk dipasang ke polinomial derajat-n, maka kita mendapatkan polinom yang cocok dengan data tersebut dengan menulis -
p = polyfit(x,y,n)Contoh
Buat file script dan ketik kode berikut -
x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67]; %data
p = polyfit(x,y,4) %get the polynomial
% Compute the values of the polyfit estimate over a finer range,
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid onSaat Anda menjalankan file, MATLAB menampilkan hasil berikut -
p =
4.1056 -47.9607 222.2598 -362.7453 191.1250Dan plot grafik berikut -
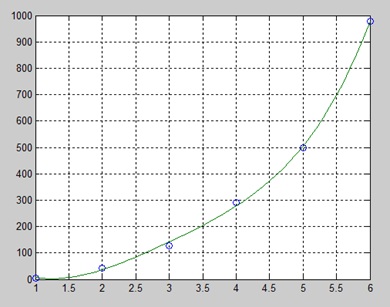
MATLAB menyediakan perintah untuk bekerja dengan transformasi, seperti transformasi Laplace dan Fourier. Transformasi digunakan dalam sains dan teknik sebagai alat untuk menyederhanakan analisis dan melihat data dari sudut lain.
Misalnya, Transformasi Fourier memungkinkan kita untuk mengubah sinyal yang direpresentasikan sebagai fungsi waktu menjadi fungsi frekuensi. Transformasi Laplace memungkinkan kita untuk mengubah persamaan diferensial menjadi persamaan aljabar.
MATLAB menyediakan laplace, fourier dan fft perintah untuk bekerja dengan transformasi Laplace, Fourier dan Fast Fourier.
Transformasi Laplace
Transformasi Laplace dari fungsi waktu f (t) diberikan oleh integral berikut -
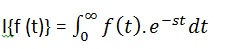
Transformasi Laplace juga dilambangkan sebagai transformasi dari f (t) menjadi F (s). Anda dapat melihat proses transformasi atau integrasi ini mengubah f (t), sebuah fungsi dari variabel simbolik t, menjadi fungsi lain F (s), dengan variabel lain s.
Transformasi Laplace mengubah persamaan diferensial menjadi persamaan aljabar. Untuk menghitung transformasi Laplace dari sebuah fungsi f (t), tulis -
laplace(f(t))Contoh
Dalam contoh ini, kami akan menghitung transformasi Laplace dari beberapa fungsi yang umum digunakan.
Buat file script dan ketik kode berikut -
syms s t a b w
laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
ans =
1/s^2
ans =
2/s^3
ans =
362880/s^10
ans =
1/(b + s)
ans =
w/(s^2 + w^2)
ans =
s/(s^2 + w^2)Transformasi Laplace Terbalik
MATLAB memungkinkan kita untuk menghitung transformasi Laplace terbalik menggunakan perintah ilaplace.
Sebagai contoh,
ilaplace(1/s^3)MATLAB akan mengeksekusi pernyataan di atas dan menampilkan hasilnya -
ans =
t^2/2Contoh
Buat file script dan ketik kode berikut -
syms s t a b w
ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))Saat Anda menjalankan file, ini akan menampilkan hasil berikut -
ans =
t^6/720
ans =
2*exp(-t*w)
ans =
cos(2*t)
ans =
ilaplace(exp(-b*t), t, x)
ans =
sin(t*w)
ans =
cos(t*w)Transformasi Fourier
Transformasi Fourier umumnya mengubah fungsi matematika waktu, f (t), menjadi fungsi baru, kadang-kadang dilambangkan dengan atau F, yang argumennya adalah frekuensi dengan satuan siklus / s (hertz) atau radian per detik. Fungsi baru ini kemudian dikenal sebagai transformasi Fourier dan / atau spektrum frekuensi dari fungsi f.
Contoh
Buat file skrip dan ketik kode berikut di dalamnya -
syms x
f = exp(-2*x^2); %our function
ezplot(f,[-2,2]) % plot of our function
FT = fourier(f) % Fourier transformSaat Anda menjalankan file, MATLAB memplot grafik berikut -
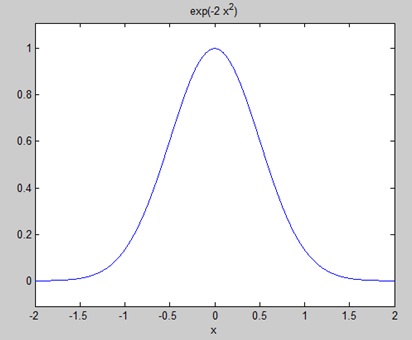
Hasil berikut ditampilkan -
FT =
(2^(1/2)*pi^(1/2)*exp(-w^2/8))/2Merencanakan transformasi Fourier sebagai -
ezplot(FT)Memberikan grafik berikut -

Transformasi Fourier Terbalik
MATLAB menyediakan ifourierperintah untuk menghitung transformasi Fourier terbalik dari suatu fungsi. Sebagai contoh,
f = ifourier(-2*exp(-abs(w)))MATLAB akan mengeksekusi pernyataan di atas dan menampilkan hasilnya -
f =
-2/(pi*(x^2 + 1))GNU Octave adalah bahasa pemrograman tingkat tinggi seperti MATLAB dan sebagian besar kompatibel dengan MATLAB. Ini juga digunakan untuk perhitungan numerik.
Oktaf memiliki fitur umum berikut dengan MATLAB -
- matriks adalah tipe data fundamental
- itu memiliki dukungan bawaan untuk bilangan kompleks
- itu memiliki fungsi dan perpustakaan matematika built-in
- itu mendukung fungsi yang ditentukan pengguna
GNU Octave juga merupakan perangkat lunak yang dapat didistribusikan ulang secara bebas. Anda dapat mendistribusikan dan / atau memodifikasinya di bawah ketentuan GNU General Public License (GPL) yang diterbitkan oleh Free Software Foundation.
MATLAB vs Oktaf
Sebagian besar program MATLAB berjalan di Oktaf, tetapi beberapa program Oktaf mungkin tidak berjalan di MATLAB karena, Oktaf mengizinkan beberapa sintaks yang tidak oleh MATLAB.
Misalnya, MATLAB hanya mendukung tanda kutip tunggal, tetapi Oktaf mendukung tanda kutip tunggal dan ganda untuk menentukan string. Jika Anda mencari tutorial tentang Oktaf, silakan ikuti tutorial ini dari awal yang mencakup MATLAB serta Oktaf.
Contoh yang Kompatibel
Hampir semua contoh yang tercakup dalam tutorial ini kompatibel dengan MATLAB serta Oktaf. Mari kita coba contoh berikut di MATLAB dan Oktaf yang menghasilkan hasil yang sama tanpa perubahan sintaks -
Contoh ini membuat peta permukaan 3D untuk fungsi g = xe - (x 2 + y 2 ) . Buat file script dan ketik kode berikut -
[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.epsSaat Anda menjalankan file, MATLAB menampilkan peta 3-D berikut -

Contoh yang Tidak Sesuai
Meskipun semua fungsi inti MATLAB tersedia dalam Oktaf, ada beberapa fungsi misalnya, Kalkulus Diferensial & Integrasi, yang tidak sama persis dalam kedua bahasa tersebut. Tutorial ini mencoba memberikan kedua jenis contoh yang berbeda dalam sintaksnya.
Pertimbangkan contoh berikut di mana MATLAB dan Oktaf menggunakan fungsi yang berbeda untuk mendapatkan luas kurva: f (x) = x 2 cos (x) untuk −4 ≤ x ≤ 9. Berikut ini adalah versi MATLAB dari kode -
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));Saat Anda menjalankan file, MATLAB memplot grafik -

Hasil berikut ditampilkan
a =
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
Area:
0.3326Tetapi untuk memberikan area kurva yang sama di Oktaf, Anda harus memanfaatkan symbolic paket sebagai berikut -
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));Simulink adalah simulasi dan lingkungan desain berbasis model untuk sistem dinamis dan tertanam, terintegrasi dengan MATLAB. Simulink, juga dikembangkan oleh MathWorks, adalah alat bahasa pemrograman grafis aliran data untuk pemodelan, simulasi, dan analisis sistem dinamis multi-domain. Ini pada dasarnya adalah alat diagram blok grafis dengan kumpulan perpustakaan blok yang dapat disesuaikan.
Ini memungkinkan Anda untuk memasukkan algoritma MATLAB ke dalam model serta mengekspor hasil simulasi ke MATLAB untuk analisis lebih lanjut.
Simulink mendukung -
- desain tingkat sistem
- simulation
- pembuatan kode otomatis
- pengujian dan verifikasi sistem tertanam
Ada beberapa produk tambahan lain yang disediakan oleh MathWorks serta produk perangkat keras dan perangkat lunak pihak ketiga yang tersedia untuk digunakan dengan Simulink.
Daftar berikut memberikan gambaran singkat tentang beberapa di antaranya -
Stateflow memungkinkan mengembangkan mesin negara dan diagram alir.
Simulink Coder memungkinkan pembuatan kode sumber C untuk implementasi sistem secara real-time secara otomatis.
xPC Target bersama dengan x86-based real-time systems menyediakan lingkungan untuk mensimulasikan dan menguji model Simulink dan Stateflow secara real-time pada sistem fisik.
Embedded Coder mendukung target tertanam tertentu.
HDL Coder memungkinkan untuk secara otomatis menghasilkan VHDL dan Verilog yang dapat disintesis.
SimEvents menyediakan perpustakaan blok bangunan grafis untuk pemodelan sistem antrian.
Simulink mampu memverifikasi dan memvalidasi model secara sistematis melalui pemeriksaan gaya pemodelan, penelusuran persyaratan, dan analisis cakupan model.
Simulink Design Verifier memungkinkan Anda mengidentifikasi kesalahan desain dan membuat skenario kasus uji untuk pemeriksaan model.
Menggunakan Simulink
Untuk membuka Simulink, ketik ruang kerja MATLAB -
simulinkSimulink dibuka dengan Library Browser. Library Browser digunakan untuk membangun model simulasi.

Di panel jendela sisi kiri, Anda akan menemukan beberapa pustaka yang dikategorikan berdasarkan berbagai sistem, mengklik masing-masing akan menampilkan blok desain di panel jendela kanan.
Model Bangunan
Untuk membuat model baru, klik Newpada toolbar Library Browser. Ini membuka jendela model baru tanpa judul.
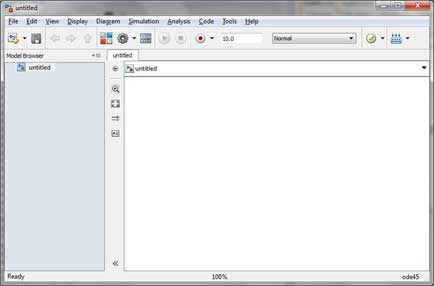
Model Simulink adalah diagram blok.
Elemen model ditambahkan dengan memilih elemen yang sesuai dari Library Browser dan menyeretnya ke jendela Model.
Sebagai alternatif, Anda dapat menyalin elemen model dan menempelkannya ke jendela model.
Contoh
Seret dan lepas item dari perpustakaan Simulink untuk membuat proyek Anda.
Untuk tujuan contoh ini, dua blok akan digunakan untuk simulasi - A Source (sinyal) dan a Sink(ruang lingkup). Generator sinyal (sumber) menghasilkan sinyal analog, yang kemudian akan divisualisasikan secara grafis oleh scope (sink).
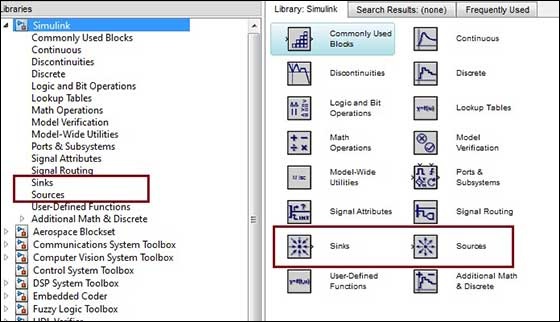
Mulailah dengan menyeret blok yang diperlukan dari perpustakaan ke jendela proyek. Kemudian, hubungkan blok bersama-sama yang dapat dilakukan dengan menyeret konektor dari titik koneksi di satu blok ke blok lainnya.
Mari kita seret blok 'Sine Wave' ke dalam model.
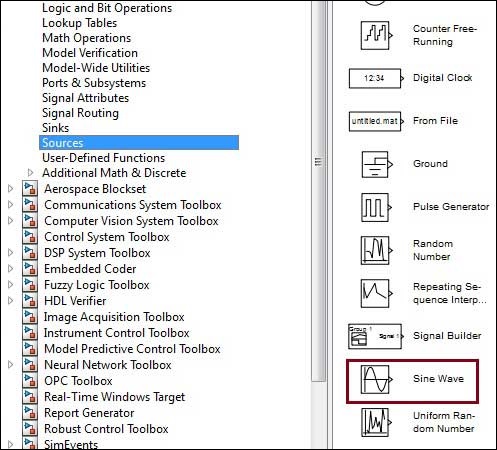
Pilih 'Sinks' dari perpustakaan dan seret blok 'Cakupan' ke dalam model.
Tarik garis sinyal dari output blok Gelombang Sinus ke input blok Scope.
Jalankan simulasi dengan menekan 'Run', menjaga semua parameter default (Anda dapat mengubahnya dari menu Simulasi)
Anda harus mendapatkan grafik di bawah ini dari ruang lingkup.