Tinggi & Jarak - Contoh Terpecahkan

Q 1 - Dari titik 375 meter dari kaki menara, puncak menara diamati pada sudut ketinggian 45 °, lalu tinggi (dalam meter) menara adalah?

J - 375

B - 450

C - 225

D - 250

Answer - A

Explanation

From the right angled triangle
Tan(45°)=  X/375
=> X = 375 m

Q 2 - Sudut elevasi menara pada titik 90 m darinya adalah cot ^-1 (4/5). Maka tinggi menara adalah

A - 45

B - 90

C - 112,5

H - 150

Answer - C

Explanation

Let cot^-1(4/5) = x 
=> cotx =  4/5   
=> tan(x) = 5/4   
From the right angled triangle
Tan(x) =  h/90 
=> h = 5/4*90 =112.5 m

Q 3 - Pada permukaan tanah, sudut ketinggian puncak menara adalah 30 °. Saat bergerak 20 meter lebih dekat, sudut ketinggian adalah 45 °. Kemudian ketinggian menara adalah

A - 10

B - √3

C - 10√3

D - 20√3

Answer - C

Explanation

Let h be the height of tower
From figure.
20 =h (  cot30 - cot60)	
20 =h (√3-1/√3) 
=> 20√3 = h (3-1) 
=> h=10√3.

Q 4 - Sudut elevasi puncak dua menara vertikal dilihat dari titik tengah garis yang menghubungkan kaki menara adalah 45 ° & 60 °. Rasio tinggi menara adalah

A - √3: 2

B - √3: 1

C - 2: √3

D - 2: 1

Answer - B

Explanation

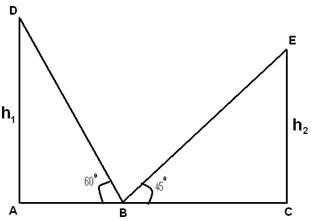
Tan(60)=h₁/AB
=> h1=√3AB
Tan(45)=h₁/BC
=> h2=BC
h1/ h2=√3/1
=> h1:h2=√3:1

Q 5 - Ketinggian dua menara adalah 90 meter dan 45 meter. Garis yang menghubungkan puncaknya membentuk sudut 450 dengan garis horizontal maka jarak antara kedua menara tersebut

A - 22,5 m

B - 45 m

C - 60 m

D - 30 m

Answer - B

Explanation

Let the distance between the towers be X 
From the right angled triangle CFD 
Tan(45)=  (90-45)/X   
=> x=45 meters

Q 6 - Dari titik P pada permukaan tanah yang datar, sudut ketinggian menara puncak adalah 60 °. Jika tinggi menara 180 m maka jarak titik P dari kaki menara adalah

A - 60√3

B - 40√3

C - 30√3

D - 20√3

Answer - A

Explanation

From ∠APB = 60° and AB = 180 m.
AB/AP= tan 60° =√3
AP=AB/√3 =180/√3=60√3

Q 7 - Puncak menara setinggi 25 meter membuat sudut elevasi 450 dengan bagian bawah tiang listrik dan sudut elevasi 30 derajat dengan puncak tiang. Tentukan tinggi tiang listrik.

A - 25√3

B - 25 ((√3-1) / √3)

C - 25 / √3

D - 25 ((1-√3) / √3)

Answer - B

Explanation

Let AB be the tower and CD be the electric pole. 
From the figure CA = DE
=> 25/(Tan(45))=(25-h)/(Tan(30))
=> 25  Tan(30) = 25-h
=> h=25-25Tan(30)
=25(1- Tan(30)) 
=25((√3-1)/√3)

Q 8 - Seorang pengamat setinggi 1,4 m berjarak 10√3 dari menara. Sudut elevasi dari matanya ke puncak menara adalah 60 °. Ketinggian menara adalah

A - 12,4 m

B - 6,2 m

C - 11,4√3 m

D - 11,4 m

Answer - D

Explanation

Let AB be the observer and CD be the tower.
Then, CE = AB = 1.4 m,
 BE = AC = 10v3 m.
DE/BE=Tan (30) =1/√3
DE=10√3/√3=10
CD=CE+DE=1.4+10=11.4 m

Pertanyaan 9 - Seorang pria sedang menonton dari puncak menara sebuah perahu melaju kencang menjauh dari menara. Perahu tersebut membuat sudut cekungan 60 ° dengan mata pria itu ketika berada pada jarak 75 meter dari menara. Setelah 10 detik, sudut depresi menjadi 45 °. Berapa perkiraan kecepatan perahu, dengan asumsi bahwa perahu tersebut berjalan di air yang tenang?

A - 54 km / jam

B - 64 km / jam

C - 24 km / jam

D - 19,8 km / jam

Answer - D

Explanation

Let AB be the tower and C and D be the positions of the boat.
Distance travelled by boat = CD
From the figure 75tan(60)=(75+CD)tan(45)
=>75√3 = 75+CD
=>CD =55 m
Speed = distance/time=55/10
=5.5 m/sec=19.8 kmph

Q 10 - Jarak horizontal antara dua menara adalah 90 m. Kemiringan sudut dari puncak yang pertama dilihat dari puncak yang kedua yang tingginya 180 m adalah 450. Kemudian tinggi yang pertama adalah

A - 90√3 m

B - 45 m

C - 90 m

D - 150 m

Answer - C

Explanation