Desain VLSI - Transistor MOS
Teknologi Complementary MOSFET (CMOS) banyak digunakan saat ini untuk membentuk sirkuit dalam berbagai aplikasi. Komputer, CPU, dan ponsel saat ini menggunakan CMOS karena beberapa keunggulan utama. CMOS menawarkan disipasi daya rendah, kecepatan relatif tinggi, margin noise tinggi di kedua status, dan akan beroperasi pada berbagai sumber dan tegangan input (asalkan tegangan sumber ditetapkan)
Untuk proses yang akan kita bahas, jenis transistor yang tersedia adalah Metal-Oxide-Semiconductor Field Effect Transistor (MOSFET). Transistor ini terbentukas a ‘sandwich’terdiri dari lapisan semikonduktor, biasanya irisan, atau wafer, dari kristal silikon tunggal; lapisan silikon dioksida (oksida) dan lapisan logam.
Struktur MOSFET
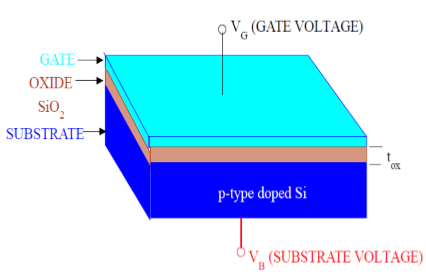
Seperti yang ditunjukkan pada gambar, struktur MOS berisi tiga lapisan -
The Metal Gate Electrode
The Insulating Oxide Layer (SiO2)
P – type Semiconductor (Substrate)
Struktur MOS membentuk kapasitor, dengan gerbang dan substrat sebagai dua pelat dan lapisan oksida sebagai bahan dielektrik. Ketebalan bahan dielektrik (SiO 2 ) biasanya antara 10 nm dan 50 nm. Konsentrasi dan distribusi pembawa di dalam substrat dapat dimanipulasi oleh tegangan eksternal yang diterapkan ke gerbang dan terminal substrat. Sekarang, untuk memahami struktur MOS, pertama-tama perhatikan sifat listrik dasar substrat semikonduktor tipe-P.
Konsentrasi pembawa dalam material semikonduktor selalu mengikuti Mass Action Law. Hukum Aksi Massa diberikan oleh -
$$n.p=n_{i}^{2}$$
Dimana,
n adalah konsentrasi pembawa elektron
p adalah konsentrasi pembawa lubang
ni adalah konsentrasi pembawa intrinsik Silikon
Sekarang asumsikan substrat yang sama didoping dengan akseptor (Boron) konsentrasi N A . Jadi, konsentrasi elektron dan lubang pada substrat tipe-p adalah
$$n_{po}=\frac{n_{i}^{2}}{N_{A}}$$
$$p_{po}=N_{A}$$
Di sini, konsentrasi doping NAadalah (10 15 sampai 10 16 cm −3 ) lebih besar dari konsentrasi intrinsik ni. Sekarang, untuk memahami struktur MOS, perhatikan diagram tingkat energi dari substrat silikon tipe-p.
Seperti yang ditunjukkan pada gambar, celah pita antara pita konduksi dan pita kelambu adalah 1.1eV. Di sini, potensial Fermi Φ F adalah perbedaan antara tingkat Fermi intrinsik (E i ) dan tingkat Fermi (E FP ).
Dimana tingkat Fermi E F tergantung pada konsentrasi doping. Potensial fermi Φ F adalah perbedaan antara tingkat Fermi intrinsik (E i ) dan tingkat Fermi (E FP ).
Secara matematis,
$$\Phi_{Fp}=\frac{E_{F}-E_{i}}{q}$$
Beda potensial antara pita konduksi dan ruang bebas disebut afinitas elektron dan dilambangkan dengan qx.
Jadi, energi yang dibutuhkan elektron untuk berpindah dari tingkat Fermi ke ruang bebas disebut fungsi kerja (qΦ S ) dan diberikan oleh
$$q\Phi _{s}=(E_{c}-E_{F})+qx$$
Gambar berikut menunjukkan diagram pita energi dari komponen yang menyusun MOS.
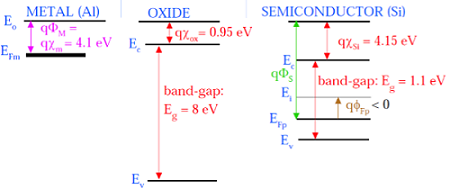
Seperti yang ditunjukkan pada gambar di atas, lapisan isolasi SiO 2 memiliki celah pita energi yang besar yaitu 8eV dan fungsi kerjanya 0,95 eV. Gerbang logam memiliki fungsi kerja 4.1eV. Disini fungsi kerjanya berbeda sehingga akan menyebabkan penurunan tegangan pada sistem MOS. Gambar yang diberikan di bawah ini menunjukkan diagram pita energi gabungan dari sistem MOS.
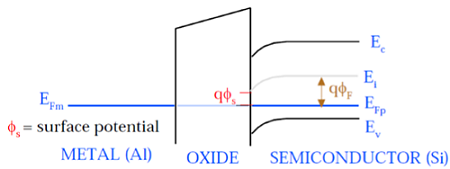
Seperti yang ditunjukkan pada gambar ini, tingkat potensial fermi gerbang logam dan semikonduktor (Si) berada pada potensial yang sama. Potensial fermi di permukaan disebut potensial permukaan Φ S dan besarnya lebih kecil dari potensial Fermi Φ F.
Bekerja dari MOSFET
MOSFET terdiri dari kapasitor MOS dengan dua persimpangan pn yang ditempatkan tertutup ke wilayah saluran dan wilayah ini dikendalikan oleh tegangan gerbang. Untuk membuat kedua persimpangan pn bias terbalik, potensial substrat dijaga lebih rendah dari pada potensial tiga terminal lainnya.
Jika tegangan gerbang akan dinaikkan melebihi tegangan ambang (V GS > V TO ), lapisan inversi akan dibentuk di permukaan dan saluran tipe-n akan dibentuk antara sumber dan saluran. Kanal tipe-n ini akan mengalirkan arus drain sesuai dengan nilai V DS .
Untuk nilai V DS yang berbeda , MOSFET dapat dioperasikan di berbagai wilayah seperti yang dijelaskan di bawah ini.
Wilayah Linear
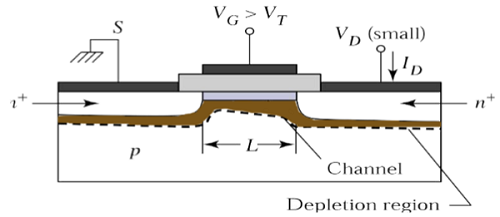
Pada V DS = 0, kesetimbangan termal ada di wilayah saluran terbalik dan arus drain I D = 0. Sekarang jika tegangan drain kecil, V DS > 0 diterapkan, arus drain sebanding dengan V DS akan mulai mengalir dari sumber ke tiriskan melalui saluran.
Saluran tersebut memberikan jalur kontinu untuk aliran arus dari sumber ke drain. Mode operasi ini disebutlinear region. Tampilan penampang MOSFET saluran-n, yang beroperasi di wilayah linier, ditunjukkan pada gambar di bawah ini.
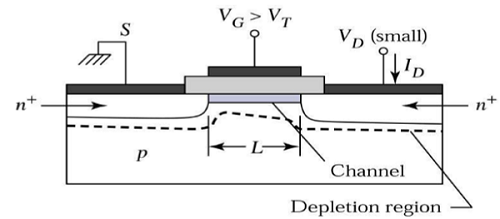
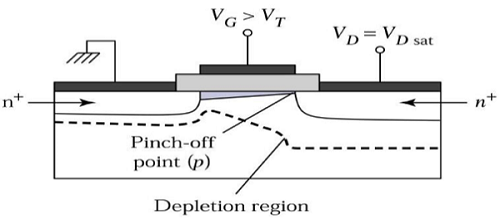
Di Tepi Wilayah Saturasi
Sekarang jika V DS meningkat, muatan di saluran dan kedalaman saluran berkurang di ujung saluran. Untuk V DS = V DSAT , biaya di saluran dikurangi menjadi nol, yang disebutpinch – off point. Tampilan penampang MOSFET saluran-n yang beroperasi di tepi wilayah saturasi ditunjukkan pada gambar di bawah ini.
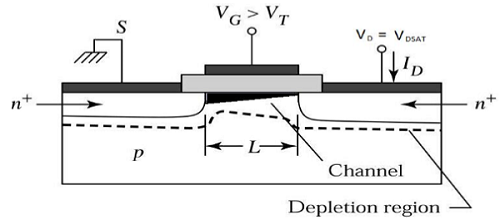
Wilayah Saturasi
Untuk V DS > V DSAT , permukaan yang habis terbentuk di dekat drain, dan dengan meningkatkan tegangan drain, daerah yang habis ini meluas ke sumber.
Mode operasi ini disebut Saturation region. Elektron yang datang dari sumber ke ujung saluran, masuk ke daerah drain - deplesi dan dipercepat menuju drain di medan listrik tinggi.
Arus MOSFET - Karakteristik Tegangan
Untuk memahami karakteristik arus - tegangan MOSFET, pendekatan saluran dilakukan. Tanpa pendekatan ini, analisis tiga dimensi sistem MOS menjadi kompleks. ItuGradual Channel Approximation (GCA) karena karakteristik tegangan arus akan mengurangi masalah analisis.
Pendekatan Saluran Bertahap (GCA)
Pertimbangkan tampilan penampang melintang saluran MOSFET yang beroperasi dalam mode linier. Di sini, sumber dan substrat dihubungkan ke tanah. V S = V B = 0. gerbang - ke - sumber (V GS ) dan tiriskan - untuk - sumber tegangan (V DS ) tegangan adalah parameter eksternal yang mengontrol arus drain I D .
Tegangan, V GS diatur ke tegangan yang lebih besar dari tegangan ambang V TO , untuk membuat saluran antara sumber dan saluran. Seperti terlihat pada gambar, arah x tegak lurus dengan permukaan dan arah y sejajar dengan permukaan.
Di sini, y = 0 di ujung sumber seperti yang ditunjukkan pada gambar. Tegangan saluran, sehubungan dengan sumbernya, diwakili olehVC(Y). Asumsikan bahwa tegangan ambang VTO adalah konstan sepanjang daerah saluran, antara y = 0 y = L. Kondisi batas untuk tegangan saluran V C adalah -
$$V_{c}\left ( y = 0 \right ) = V_{s} = 0 \,and\,V_{c}\left ( y = L \right ) = V_{DS}$$
Kita juga bisa berasumsi seperti itu
$$V_{GS}\geq V_{TO}$$ dan
$$V_{GD} = V_{GS}-V_{DS}\geq V_{TO}$$
Misalkan Q1 (y) adalah muatan elektron bergerak total pada lapisan inversi permukaan. Muatan elektron ini dapat dinyatakan sebagai -
$$Q1(y)=-C_{ox}.[V_{GS}-V_{C(Y)}-V_{TO}]$$
Gambar yang diberikan di bawah ini menunjukkan geometri spasial dari lapisan inversi permukaan dan menunjukkan dimensinya. Lapisan inversi meruncing saat kita berpindah dari saluran ke sumber. Sekarang, jika kita mempertimbangkan dy daerah kecil dari panjang saluran L maka tahanan tambahan dR yang ditawarkan oleh daerah ini dapat dinyatakan sebagai -
$$dR=-\frac{dy}{w.\mu _{n}.Q1(y)}$$
Di sini, tanda minus ini disebabkan oleh polaritas negatif dari inversi muatan lapisan Q1 dan μ n adalah mobilitas permukaan, yang konstan. Sekarang, gantikan nilai Q1 (y) ke dalam persamaan dR -
$$dR=-\frac{dy}{w.\mu _{n}.\left \{ -C_{ox}\left [ V_{GS}-V_{C\left ( Y \right )} \right ]-V_{TO} \right \}}$$
$$dR=\frac{dy}{w.\mu _{n}.C_{ox}\left [ V_{GS}-V_{C\left ( Y \right )} \right ]-V_{TO}}$$
Sekarang penurunan tegangan di daerah dy kecil dapat diberikan oleh
$$dV_{c}=I_{D}.dR$$
Masukkan nilai dR pada persamaan di atas
$$dV_{C}=I_{D}.\frac{dy}{w.\mu_{n}.C_{ox}\left [ V_{GS}-V_{C(Y)} \right ]-V_{TO}}$$
$$w.\mu _{n}.C_{ox}\left [ V_{GS}-V_{C(Y)}-V_{TO} \right ].dV_{C}=I_{D}.dy$$
Untuk mendapatkan ID arus drain di seluruh wilayah saluran, persamaan di atas dapat diintegrasikan di sepanjang saluran dari y = 0 ke y = L dan tegangan V C (y) = 0 ke V C (y) = V DS ,
$$C_{ox}.w.\mu _{n}.\int_{V_{c}=0}^{V_{DS}} \left [ V_{GS}-V_{C\left ( Y \right )}-V_{TO} \right ].dV_{C} = \int_{Y=0}^{L}I_{D}.dy$$
$$\frac{C_{ox}.w.\mu _{n}}{2}\left ( 2\left [ V_{GS}-V_{TO} \right ] V_{DS}-V_{DS}^{2}\right ) = I_{D}\left [ L-0 \right ]$$
$$I_{D} = \frac{C_{ox}.\mu _{n}}{2}.\frac{w}{L}\left ( 2\left [ V_{GS}-V_{TO} \right ]V_{DS}-V_{DS}^{2} \right )$$
Untuk wilayah linier V DS <V GS - V TO . Untuk wilayah saturasi, nilai V DS lebih besar dari (V GS - V TO ). Oleh karena itu, untuk wilayah saturasi V DS = (V GS - V TO ).
$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{\left [ 2V_{DS} \right ]V_{DS}-V_{DS}^{2}}{L} \right )$$
$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{2V_{DS}^{2}-V_{DS}^{2}}{L} \right )$$
$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{V_{DS}^{2}}{L} \right )$$
$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{\left [ V_{GS}-V_{TO} \right ]^{2}}{L} \right )$$