Desain VLSI - Panduan Cepat

Integrasi skala sangat besar (VLSI) adalah proses pembuatan file integrated circuit (IC) dengan menggabungkan ribuan transistorsmenjadi satu chip. VLSI dimulai pada 1970-an ketika komplekssemiconductor dan communicationteknologi sedang dikembangkan. Itumicroprocessor adalah perangkat VLSI.

Sebelum teknologi VLSI diperkenalkan, kebanyakan IC memiliki serangkaian fungsi terbatas yang dapat mereka lakukan. Sebuahelectronic circuit mungkin terdiri dari a CPU, ROM, RAM dan lainnya glue logic. VLSI memungkinkan desainer IC menambahkan semua ini ke dalam satu chip.

Industri elektronik telah mencapai pertumbuhan yang fenomenal selama beberapa dekade terakhir, terutama karena kemajuan pesat dalam teknologi integrasi skala besar dan aplikasi desain sistem. Dengan munculnya desain integrasi skala sangat besar (VLSI), jumlah aplikasi sirkuit terintegrasi (IC) dalam komputasi kinerja tinggi, kontrol, telekomunikasi, pemrosesan gambar dan video, dan elektronik konsumen telah meningkat dengan sangat cepat.

Teknologi mutakhir saat ini seperti resolusi tinggi dan bit-rate rendah serta komunikasi seluler memberikan pengguna akhir sejumlah aplikasi, daya pemrosesan, dan portabilitas yang luar biasa. Tren ini diharapkan berkembang pesat, dengan implikasi yang sangat penting pada desain VLSI dan desain sistem.

Alur Desain VLSI

Alur desain rangkaian IC VLSI ditunjukkan pada gambar di bawah ini. Berbagai tingkat desain diberi nomor dan blok menunjukkan proses dalam aliran desain.

Spesifikasi didahulukan, mereka menjelaskan secara abstrak, fungsionalitas, antarmuka, dan arsitektur rangkaian IC digital yang akan dirancang.

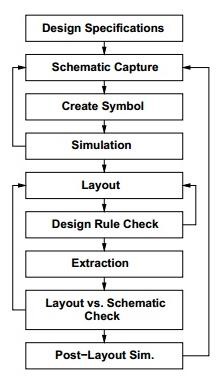
Deskripsi perilaku kemudian dibuat untuk menganalisis desain dalam hal fungsionalitas, kinerja, kepatuhan terhadap standar yang diberikan, dan spesifikasi lainnya.

Deskripsi RTL dilakukan menggunakan HDL. Deskripsi RTL ini disimulasikan untuk menguji fungsionalitas. Mulai dari sini dan seterusnya kami membutuhkan bantuan alat EDA.

Deskripsi RTL kemudian diubah menjadi netlist tingkat gerbang menggunakan alat sintesis logika. Netlist level gerbang adalah deskripsi rangkaian dalam hal gerbang dan koneksi di antara mereka, yang dibuat sedemikian rupa sehingga memenuhi spesifikasi waktu, daya, dan area.

Akhirnya, tata letak fisik dibuat, yang akan diverifikasi dan kemudian dikirim ke fabrikasi.

Diagram Y

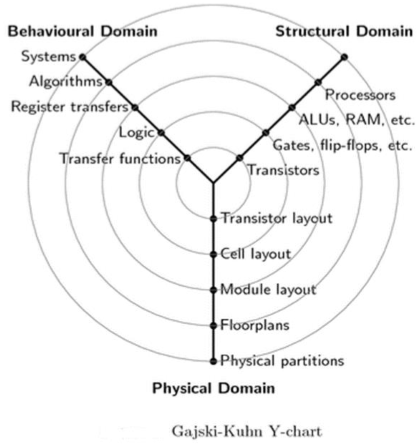
Gajski-Kuhn Y-chart adalah model yang menangkap pertimbangan dalam mendesain perangkat semikonduktor.

Tiga domain dari bagan Gajski-Kuhn Y berada pada sumbu radial. Setiap domain dapat dibagi menjadi beberapa level abstraksi, menggunakan cincin konsentris.

Di tingkat atas (cincin luar), kami mempertimbangkan arsitektur chip; di tingkat yang lebih rendah (cincin bagian dalam), kami secara berturut-turut menyempurnakan desain menjadi implementasi terperinci yang lebih halus -

Membuat deskripsi struktural dari perilaku dicapai melalui proses sintesis tingkat tinggi atau sintesis logis.

Membuat deskripsi fisik dari yang struktural dicapai melalui sintesis tata letak.

Desain Hierarki-Struktural

Hierarki desain melibatkan prinsip "Divide and Conquer". Ini tidak lain adalah membagi tugas menjadi tugas-tugas yang lebih kecil hingga mencapai tingkat yang paling sederhana. Proses ini paling cocok karena evolusi terakhir desain menjadi begitu sederhana sehingga pembuatannya menjadi lebih mudah.

Kita dapat mendesain tugas yang diberikan ke dalam domain proses aliran desain (Perilaku, Struktural, dan Geometris). Untuk memahami ini, mari kita ambil contoh mendesain adder 16-bit, seperti yang ditunjukkan pada gambar di bawah ini.

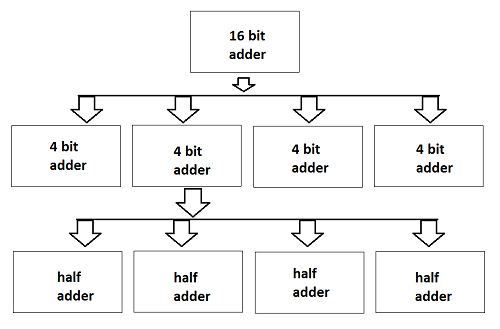
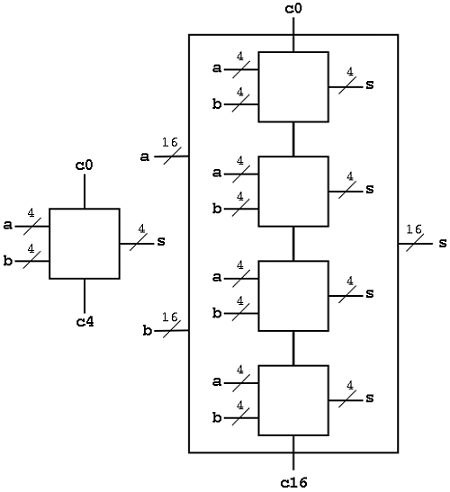
Di sini, seluruh chip penambah 16 bit dibagi menjadi empat modul penambah 4-bit. Selanjutnya, bagi penambah 4-bit menjadi penambah 1-bit atau penambah setengah. Penambahan 1 bit adalah proses perancangan yang paling sederhana dan sirkuit internalnya juga mudah dibuat pada chip. Sekarang, dengan menghubungkan keempat penambah terakhir, kita dapat mendesain penambah 4-bit dan melanjutkan, kita dapat merancang penambah 16-bit.

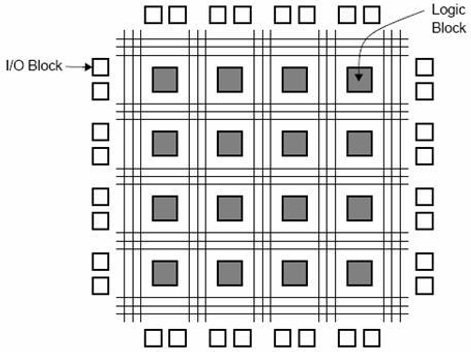
FPGA - Pendahuluan

Bentuk lengkap FPGA adalah "Field Programmable Gate Array". Ini berisi sepuluh ribu hingga lebih dari satu juta gerbang logika dengan interkoneksi yang dapat diprogram. Interkoneksi yang dapat diprogram tersedia bagi pengguna atau desainer untuk menjalankan fungsi yang diberikan dengan mudah. Model chip FPGA khas ditunjukkan pada gambar yang diberikan. Ada blok I / O yang didesain dan diberi nomor sesuai fungsinya. Untuk setiap modul komposisi level logika, adaCLB’s (Configurable Logic Blocks).

CLB melakukan operasi logika yang diberikan ke modul. Koneksi antar blok CLB dan I / O dibuat dengan bantuan saluran perutean horizontal, saluran perutean vertikal, dan PSM (Programmable Multiplexer).

Jumlah CLB yang dikandungnya hanya menentukan kompleksitas FPGA. Fungsi CLB dan PSM dirancang oleh VHDL atau bahasa deskriptif perangkat keras lainnya. Setelah pemrograman, CLB dan PSM ditempatkan pada chip dan dihubungkan satu sama lain dengan saluran perutean.

Keuntungan

• Ini membutuhkan waktu yang sangat singkat; mulai dari proses desain hingga chip fungsional.
• Tidak ada langkah pembuatan fisik yang terlibat di dalamnya.
• Satu-satunya kelemahan adalah, itu lebih mahal daripada gaya lainnya.

Desain Array Gerbang

Itu gate array (GA)menempati urutan kedua setelah FPGA, dalam hal kemampuan pembuatan prototipe yang cepat. Sementara pemrograman pengguna penting untuk implementasi desain chip FPGA, desain dan pemrosesan topeng logam digunakan untuk GA. Implementasi gate array membutuhkan proses manufaktur dua langkah.

Tahap pertama menghasilkan array transistor yang tidak terikat pada setiap chip GA. Chip yang tidak terikat ini dapat disimpan untuk penyesuaian nanti, yang diselesaikan dengan menentukan interkoneksi logam antara transistor array. Pola interkoneksi logam dilakukan pada akhir proses fabrikasi chip, sehingga waktu putar balik masih bisa singkat, beberapa hari hingga beberapa minggu. Gambar yang diberikan di bawah ini menunjukkan langkah-langkah pemrosesan dasar untuk implementasi array gerbang.

Platform array gerbang tipikal menggunakan area khusus yang disebut saluran, untuk perutean antar sel antara baris atau kolom transistor MOS. Mereka menyederhanakan interkoneksi. Pola interkoneksi yang menjalankan gerbang logika dasar disimpan di perpustakaan, yang kemudian dapat digunakan untuk menyesuaikan baris transistor yang tidak terikat menurut netlist.

Di sebagian besar GA modern, beberapa lapisan logam digunakan untuk perutean saluran. Dengan penggunaan beberapa lapisan yang saling berhubungan, perutean dapat dicapai melalui area sel aktif; sehingga saluran perutean dapat dihapus seperti pada chip Sea-of-Gates (SOG). Di sini, seluruh permukaan chip ditutupi dengan transistor nMOS dan pMOS tanpa ikatan. Transistor tetangga dapat dikustomisasi menggunakan topeng logam untuk membentuk gerbang logika dasar.

Untuk perutean antar sel, beberapa transistor yang tidak terikat harus dikorbankan. Gaya desain ini menghasilkan lebih banyak fleksibilitas untuk interkoneksi dan biasanya dalam kepadatan yang lebih tinggi. Faktor pemanfaatan chip GA diukur dengan luas chip yang digunakan dibagi dengan total luas chip. Ini lebih tinggi dari FPGA dan begitu juga kecepatan chip.

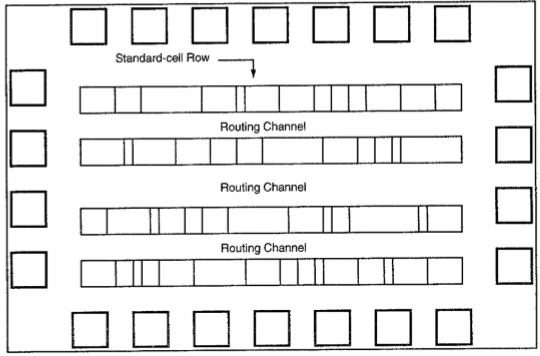
Desain Berbasis Sel Standar

Desain berbasis sel standar memerlukan pengembangan set masker kustom lengkap. Sel standar juga dikenal sebagai polycell. Dalam pendekatan ini, semua sel logika yang umum digunakan dikembangkan, dikarakterisasi, dan disimpan dalam pustaka sel standar.

Sebuah perpustakaan mungkin berisi beberapa ratus sel termasuk inverter, gerbang NAND, gerbang NOR, AOI kompleks, gerbang OAI, D-latch dan Flip-flop. Setiap tipe gerbang dapat diimplementasikan dalam beberapa versi untuk memberikan kemampuan mengemudi yang memadai untuk berbagai fan-out. Gerbang inverter dapat memiliki ukuran standar, ukuran ganda, dan ukuran empat kali lipat sehingga desainer chip dapat memilih ukuran yang tepat untuk mendapatkan kecepatan sirkuit dan kepadatan tata letak yang tinggi.

Setiap sel dikarakterisasi menurut beberapa kategori karakterisasi yang berbeda, seperti,

• Waktu tunda versus kapasitansi beban
• Model simulasi sirkuit
• Model simulasi waktu
• Model simulasi kesalahan
• Data sel untuk tempat-dan-rute
• Sembunyikan data

Untuk penempatan otomatis sel dan perutean, setiap tata letak sel dirancang dengan ketinggian tetap, sehingga sejumlah sel dapat dibatasi berdampingan untuk membentuk baris. Rel listrik dan ground sejajar dengan batas atas dan bawah sel. Sehingga, sel tetangga berbagi bus daya yang sama dan bus tanah yang sama. Gambar yang ditampilkan di bawah ini adalah denah lantai untuk desain berbasis sel standar.

Desain Kustom Penuh

Dalam desain kustom penuh, seluruh desain masker dibuat baru, tanpa menggunakan pustaka apa pun. Biaya pengembangan gaya desain ini meningkat. Dengan demikian, konsep penggunaan kembali desain menjadi terkenal untuk mengurangi waktu siklus desain dan biaya pengembangan.

Desain kustom lengkap yang paling sulit dapat berupa desain sel memori, baik itu statis maupun dinamis. Untuk desain chip logika, negosiasi yang baik dapat diperoleh dengan menggunakan kombinasi gaya desain yang berbeda pada chip yang sama, yaitu sel standar, sel jalur data, danprogrammable logic arrays (PLAs).

Praktisnya, desainer melakukan full custom layout, yaitu geometri, orientasi, dan penempatan setiap transistor. Produktivitas desain biasanya sangat rendah; biasanya beberapa puluh transistor per hari, per desainer. Dalam CMOS VLSI digital, desain kustom penuh hampir tidak digunakan karena biaya tenaga kerja yang tinggi. Gaya desain ini mencakup desain produk bervolume tinggi seperti chip memori, mikroprosesor performa tinggi, dan FPGA.

Teknologi Complementary MOSFET (CMOS) banyak digunakan saat ini untuk membentuk sirkuit dalam berbagai aplikasi. Komputer, CPU, dan ponsel saat ini menggunakan CMOS karena beberapa keunggulan utama. CMOS menawarkan disipasi daya rendah, kecepatan relatif tinggi, margin noise tinggi di kedua status, dan akan beroperasi pada berbagai sumber dan tegangan input (asalkan tegangan sumber ditetapkan)

Untuk proses yang akan kita bahas, jenis transistor yang tersedia adalah Metal-Oxide-Semiconductor Field Effect Transistor (MOSFET). Transistor ini terbentukas a ‘sandwich’terdiri dari lapisan semikonduktor, biasanya irisan, atau wafer, dari kristal silikon tunggal; lapisan silikon dioksida (oksida) dan lapisan logam.

Struktur MOSFET

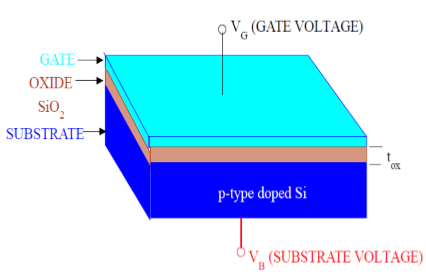
Seperti yang ditunjukkan pada gambar, struktur MOS berisi tiga lapisan -

• The Metal Gate Electrode

• The Insulating Oxide Layer (SiO₂)

• P – type Semiconductor (Substrate)

Struktur MOS membentuk kapasitor, dengan gerbang dan substrat sebagai dua pelat dan lapisan oksida sebagai bahan dielektrik. Ketebalan bahan dielektrik (SiO ₂ ) biasanya antara 10 nm dan 50 nm. Konsentrasi dan distribusi pembawa di dalam substrat dapat dimanipulasi dengan tegangan eksternal yang diterapkan ke gerbang dan terminal substrat. Sekarang, untuk memahami struktur MOS, pertama-tama perhatikan sifat listrik dasar substrat semikonduktor Tipe-P.

Konsentrasi pembawa dalam material semikonduktor selalu mengikuti Mass Action Law. Hukum Aksi Massa diberikan oleh -

$$n.p=n_{i}^{2}$$

Dimana,

• n adalah konsentrasi pembawa elektron

• p adalah konsentrasi pembawa lubang

• n_i adalah konsentrasi pembawa intrinsik Silikon

Sekarang asumsikan substrat yang sama didoping dengan akseptor (Boron) konsentrasi N _A . Jadi, konsentrasi elektron dan lubang pada substrat tipe-p adalah

$$n_{po}=\frac{n_{i}^{2}}{N_{A}}$$

$$p_{po}=N_{A}$$

Di sini, konsentrasi doping N_Aadalah (10 ¹⁵ sampai 10 ¹⁶ cm ⁻³ ) lebih besar dari konsentrasi intrinsik ni. Sekarang, untuk memahami struktur MOS, perhatikan diagram tingkat energi dari substrat silikon tipe-p.

Seperti yang ditunjukkan pada gambar, celah pita antara pita konduksi dan pita kelambu adalah 1.1eV. Di sini, potensial Fermi Φ _F adalah perbedaan antara tingkat Fermi intrinsik (E _i ) dan tingkat Fermi (E _FP ).

Dimana tingkat Fermi E _F tergantung pada konsentrasi doping. Potensial fermi Φ _F adalah perbedaan antara tingkat Fermi intrinsik (E _i ) dan tingkat Fermi (E _FP ).

Secara matematis,

$$\Phi_{Fp}=\frac{E_{F}-E_{i}}{q}$$

Beda potensial antara pita konduksi dan ruang bebas disebut afinitas elektron dan dilambangkan dengan qx.

Jadi, energi yang dibutuhkan elektron untuk berpindah dari tingkat Fermi ke ruang bebas disebut fungsi kerja (qΦ _S ) dan diberikan oleh

$$q\Phi _{s}=(E_{c}-E_{F})+qx$$

Gambar berikut menunjukkan diagram pita energi komponen penyusun MOS.

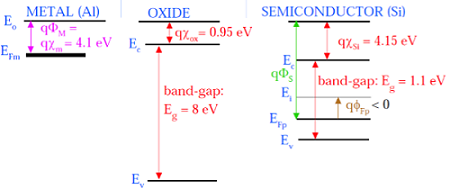
Seperti yang terlihat pada gambar di atas, lapisan isolasi SiO ₂ memiliki celah pita energi yang besar yaitu 8eV dan fungsi kerjanya adalah 0,95 eV. Gerbang logam memiliki fungsi kerja 4.1eV. Disini fungsi kerjanya berbeda sehingga akan menyebabkan penurunan tegangan pada sistem MOS. Gambar yang diberikan di bawah ini menunjukkan diagram pita energi gabungan dari sistem MOS.

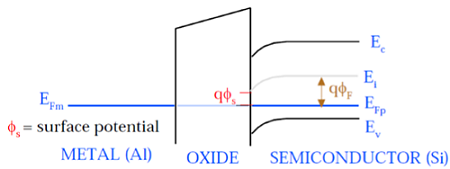
Seperti yang ditunjukkan pada gambar ini, tingkat potensial fermi gerbang logam dan semikonduktor (Si) berada pada potensial yang sama. Potensial fermi di permukaan disebut potensial permukaan Φ _S dan besarnya lebih kecil dari potensial Fermi Φ _F.

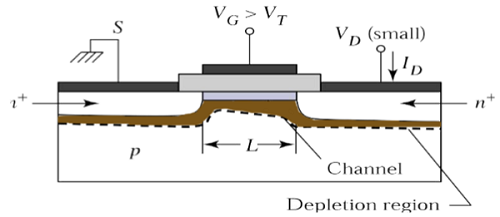
Bekerja dari MOSFET

MOSFET terdiri dari kapasitor MOS dengan dua sambungan pn yang ditempatkan tertutup ke wilayah saluran dan wilayah ini dikendalikan oleh tegangan gerbang. Untuk membuat kedua persimpangan pn bias terbalik, potensial substrat dijaga lebih rendah dari pada potensial tiga terminal lainnya.

Jika tegangan gerbang akan dinaikkan melebihi tegangan ambang (V _GS > V _TO ), lapisan inversi akan dibentuk di permukaan dan saluran tipe-n akan dibentuk antara sumber dan saluran. Kanal tipe-n ini akan mengalirkan arus drain sesuai dengan nilai V _DS .

Untuk nilai V _{DS yang berbeda} , MOSFET dapat dioperasikan di berbagai wilayah seperti yang dijelaskan di bawah ini.

Wilayah Linear

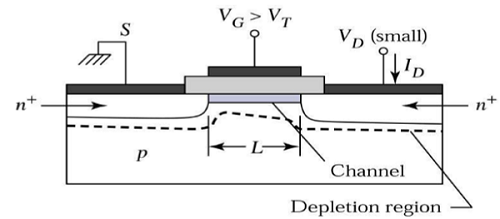
Pada V _DS = 0, kesetimbangan termal ada di daerah saluran terbalik dan arus drain I _D = 0. Sekarang jika tegangan drain kecil, V _DS > 0 diterapkan, arus drain sebanding dengan V _DS akan mulai mengalir dari sumber ke tiriskan melalui saluran.

Saluran tersebut memberikan jalur kontinu untuk aliran arus dari sumber ke drain. Mode operasi ini disebutlinear region. Tampilan penampang MOSFET saluran-n, yang beroperasi di wilayah linier, ditunjukkan pada gambar di bawah ini.

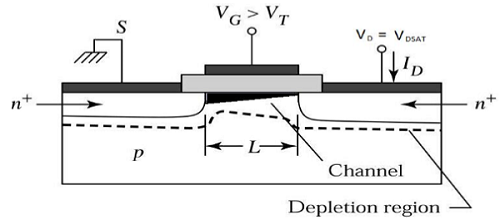
Di Tepi Wilayah Saturasi

Sekarang jika V _DS meningkat, muatan di saluran dan kedalaman saluran berkurang di ujung saluran. Untuk V _DS = V _DSAT , biaya di saluran dikurangi menjadi nol, yang disebutpinch – off point. Tampilan penampang melintang MOSFET saluran-n yang beroperasi di tepi wilayah saturasi ditunjukkan pada gambar di bawah ini.

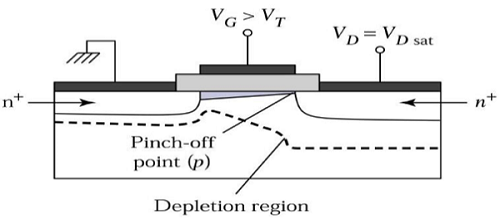
Wilayah Saturasi

Untuk V _DS > V _DSAT , permukaan yang habis terbentuk di dekat saluran, dan dengan meningkatkan tegangan saluran, daerah yang habis ini meluas ke sumbernya.

Mode operasi ini disebut Saturation region. Elektron yang datang dari sumber ke ujung saluran, masuk ke daerah drain - deplesi dan dipercepat menuju drain di medan listrik tinggi.

Arus MOSFET - Karakteristik Tegangan

Untuk memahami karakteristik arus - tegangan pada MOSFET, perkiraan saluran dilakukan. Tanpa pendekatan ini, analisis tiga dimensi sistem MOS menjadi kompleks. ItuGradual Channel Approximation (GCA) karena karakteristik tegangan arus akan mengurangi masalah analisis.

Perkiraan Saluran Bertahap (GCA)

Pertimbangkan tampilan penampang melintang saluran MOSFET yang beroperasi dalam mode linier. Di sini, sumber dan substrat dihubungkan ke tanah. V _S = V _B = 0. gerbang - ke - sumber (V _GS ) dan tiriskan - untuk - sumber tegangan (V _DS ) tegangan adalah parameter eksternal yang mengontrol arus drain I _D .

Tegangan, V _GS diatur ke tegangan yang lebih besar dari tegangan ambang V _TO , untuk membuat saluran antara sumber dan saluran. Seperti terlihat pada gambar, arah x tegak lurus dengan permukaan dan arah y sejajar dengan permukaan.

Di sini, y = 0 di ujung sumber seperti yang ditunjukkan pada gambar. Tegangan saluran, sehubungan dengan sumbernya, diwakili olehV_C(Y). Asumsikan bahwa tegangan ambang VTO adalah konstan sepanjang daerah saluran, antara y = 0 y = L. Kondisi batas untuk tegangan saluran V _C adalah -

$$V_{c}\left ( y = 0 \right ) = V_{s} = 0 \,and\,V_{c}\left ( y = L \right ) = V_{DS}$$

Kita juga bisa berasumsi seperti itu

$$V_{GS}\geq V_{TO}$$ dan

$$V_{GD} = V_{GS}-V_{DS}\geq V_{TO}$$

Misalkan Q1 (y) adalah muatan total elektron bergerak di lapisan inversi permukaan. Muatan elektron ini dapat dinyatakan sebagai -

$$Q1(y)=-C_{ox}.[V_{GS}-V_{C(Y)}-V_{TO}]$$

Gambar yang diberikan di bawah ini menunjukkan geometri spasial dari lapisan inversi permukaan dan menunjukkan dimensinya. Lapisan inversi meruncing saat kita berpindah dari saluran ke sumber. Sekarang, jika kita mempertimbangkan dy daerah kecil dari panjang saluran L maka tahanan tambahan dR yang ditawarkan oleh daerah ini dapat dinyatakan sebagai -

$$dR=-\frac{dy}{w.\mu _{n}.Q1(y)}$$

Di sini, tanda minus ini disebabkan oleh polaritas negatif dari inversi muatan lapisan Q1 dan μ _n adalah mobilitas permukaan, yang konstan. Sekarang, gantikan nilai Q1 (y) ke dalam persamaan dR -

$$dR=-\frac{dy}{w.\mu _{n}.\left \{ -C_{ox}\left [ V_{GS}-V_{C\left ( Y \right )} \right ]-V_{TO} \right \}}$$

$$dR=\frac{dy}{w.\mu _{n}.C_{ox}\left [ V_{GS}-V_{C\left ( Y \right )} \right ]-V_{TO}}$$

Sekarang penurunan tegangan di daerah dy kecil dapat diberikan oleh

$$dV_{c}=I_{D}.dR$$

Masukkan nilai dR pada persamaan di atas

$$dV_{C}=I_{D}.\frac{dy}{w.\mu_{n}.C_{ox}\left [ V_{GS}-V_{C(Y)} \right ]-V_{TO}}$$

$$w.\mu _{n}.C_{ox}\left [ V_{GS}-V_{C(Y)}-V_{TO} \right ].dV_{C}=I_{D}.dy$$

Untuk mendapatkan ID arus drain di seluruh wilayah saluran, persamaan di atas dapat diintegrasikan di sepanjang saluran dari y = 0 ke y = L dan tegangan V _{C (y)} = 0 ke V _{C (y)} = V _DS ,

$$C_{ox}.w.\mu _{n}.\int_{V_{c}=0}^{V_{DS}} \left [ V_{GS}-V_{C\left ( Y \right )}-V_{TO} \right ].dV_{C} = \int_{Y=0}^{L}I_{D}.dy$$

$$\frac{C_{ox}.w.\mu _{n}}{2}\left ( 2\left [ V_{GS}-V_{TO} \right ] V_{DS}-V_{DS}^{2}\right ) = I_{D}\left [ L-0 \right ]$$

$$I_{D} = \frac{C_{ox}.\mu _{n}}{2}.\frac{w}{L}\left ( 2\left [ V_{GS}-V_{TO} \right ]V_{DS}-V_{DS}^{2} \right )$$

Untuk wilayah linier V _DS <V _GS - V _TO . Untuk wilayah saturasi, nilai V _DS lebih besar dari (V _GS - V _TO ). Oleh karena itu, untuk wilayah saturasi V _DS = (V _GS - V _TO ).

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{\left [ 2V_{DS} \right ]V_{DS}-V_{DS}^{2}}{L} \right )$$

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{2V_{DS}^{2}-V_{DS}^{2}}{L} \right )$$

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{V_{DS}^{2}}{L} \right )$$

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{\left [ V_{GS}-V_{TO} \right ]^{2}}{L} \right )$$

Inverter benar-benar merupakan inti dari semua desain digital. Setelah operasi dan propertinya dipahami dengan jelas, merancang struktur yang lebih rumit seperti gerbang NAND, adder, pengganda, dan mikroprosesor sangat disederhanakan. Perilaku listrik dari rangkaian kompleks ini dapat hampir sepenuhnya diturunkan dengan mengekstrapolasi hasil yang diperoleh untuk inverter.

Analisis inverter dapat diperluas untuk menjelaskan perilaku gerbang yang lebih kompleks seperti NAND, NOR, atau XOR, yang pada gilirannya membentuk blok bangunan untuk modul seperti pengganda dan prosesor. Dalam bab ini, kami fokus pada satu inkarnasi tunggal dari gerbang inverter, menjadi CMOS inverter statis - atau singkatnya inverter CMOS. Ini tentunya yang paling populer saat ini dan oleh karena itu perlu perhatian khusus kami.

Prinsip operasi

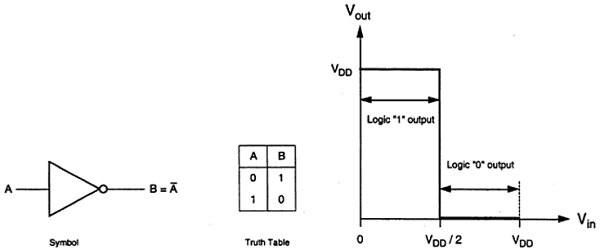
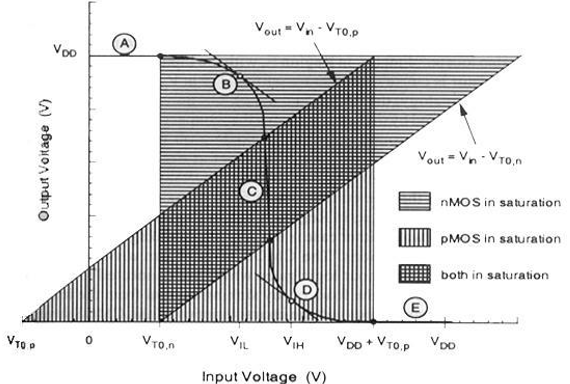
Simbol logika dan tabel kebenaran inverter ideal ditunjukkan pada gambar di bawah ini. Di sini A adalah input dan B adalah output terbalik yang diwakili oleh tegangan simpulnya. Dengan menggunakan logika positif, nilai Boolean dari logika 1 diwakili oleh V _dd dan logika 0 diwakili oleh 0. V _th adalah tegangan ambang inverter, yaitu V _dd / 2, di mana V _dd adalah tegangan keluaran.

Output dialihkan dari 0 ke V _dd ketika input kurang dari V _th . Jadi, untuk 0 <V _in <V _th output sama dengan input logika 0 dan V _th <V _di <V _dd sama dengan input logika 1 untuk inverter.

Karakteristik yang ditunjukkan pada gambar adalah ideal. Struktur rangkaian umum dari inverter nMOS ditunjukkan pada gambar di bawah ini.

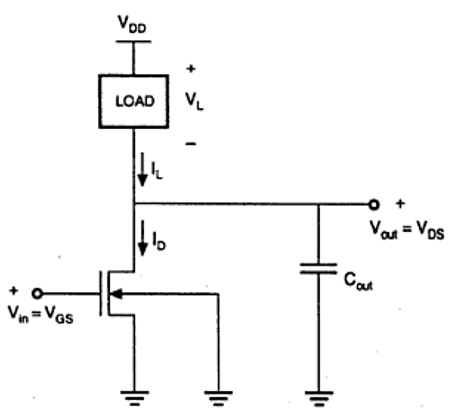
Dari gambar yang diberikan, kita dapat melihat bahwa tegangan input inverter sama dengan tegangan gerbang ke sumber transistor nMOS dan tegangan keluaran inverter sama dengan tegangan drain ke sumber transistor nMOS. Sumber tegangan substrat nMOS juga disebut driver untuk transistor yang di-ground; jadi V _SS = 0. Node keluaran dihubungkan dengan kapasitansi gabungan yang digunakan untuk VTC.

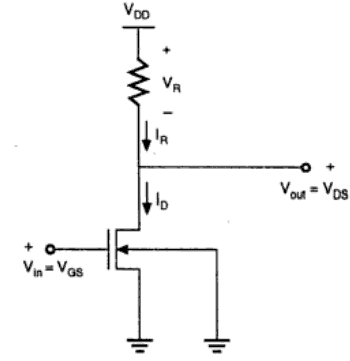
Inverter Beban Resistif

Struktur dasar inverter beban resistif ditunjukkan pada gambar di bawah ini. Di sini, peningkatan tipe nMOS bertindak sebagai transistor driver. Beban terdiri dari linear resistor R sederhana _L . Catu daya dari rangkaian tersebut adalah V _DD dan arus drain I _D adalah sama dengan arus beban I _R .

Operasi Sirkuit

Ketika input transistor driver kurang dari tegangan ambang V _TH (V _dalam <V _TH ), transistor driver berada di daerah cut-off dan tidak mengalirkan arus apapun. Jadi, penurunan tegangan pada resistor beban adalah NOL dan tegangan keluaran sama dengan V _DD . Sekarang, ketika tegangan input semakin meningkat, transistor driver akan mulai mengalirkan arus bukan nol dan nMOS masuk ke wilayah saturasi.

Secara matematis,

$$I_{D} = \frac{K_{n}}{2}\left [ V_{GS}-V_{TO} \right ]^{2}$$

Meningkatkan tegangan input lebih lanjut, transistor driver akan masuk ke wilayah linier dan output dari transistor driver berkurang.

$$I_{D} = \frac{K_{n}}{2}2\left [ V_{GS}-V_{TO} \right ]V_{DS}-V_{DS}^{2}$$

VTC dari inverter beban resistif, ditunjukkan di bawah, menunjukkan mode operasi transistor driver dan titik tegangan.

Inverter dengan Beban MOSFET tipe N.

Keuntungan utama menggunakan MOSFET sebagai perangkat beban adalah area silikon yang ditempati oleh transistor lebih kecil dari area yang ditempati oleh beban resistif. Di sini MOSFET adalah beban aktif dan inverter dengan beban aktif memberikan kinerja yang lebih baik daripada inverter dengan beban resistif.

Peningkatan Beban NMOS

Dua inverter dengan perangkat beban tipe peningkatan ditunjukkan pada gambar. Transistor beban dapat dioperasikan baik di wilayah saturasi atau di wilayah linier, tergantung pada tegangan bias yang diterapkan ke terminal gerbangnya. Inverter beban tambahan jenuh ditunjukkan pada gambar. (Sebuah). Hal ini membutuhkan suplai tegangan tunggal dan proses fabrikasi sederhana dan begitu V _OH terbatas pada V _DD - V _T .

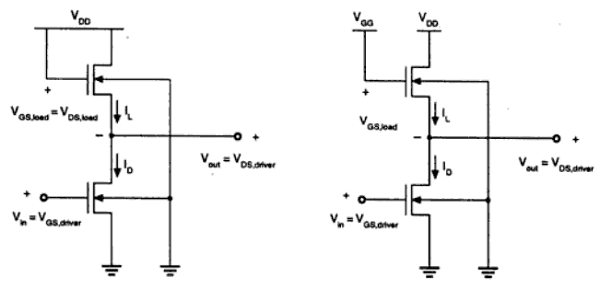
Inverter beban peningkatan linier ditunjukkan pada gambar. (b). Itu selalu beroperasi di wilayah linier; jadi level V _OH sama dengan V _DD .

Inverter beban linier memiliki margin kebisingan yang lebih tinggi dibandingkan dengan inverter peningkatan jenuh. Tapi, kelemahan dari inverter peningkatan linier adalah, ini membutuhkan dua catu daya terpisah dan kedua sirkuit menderita disipasi daya tinggi. Oleh karena itu, inverter tambahan tidak digunakan dalam aplikasi digital skala besar.

Beban Deplesi NMOS

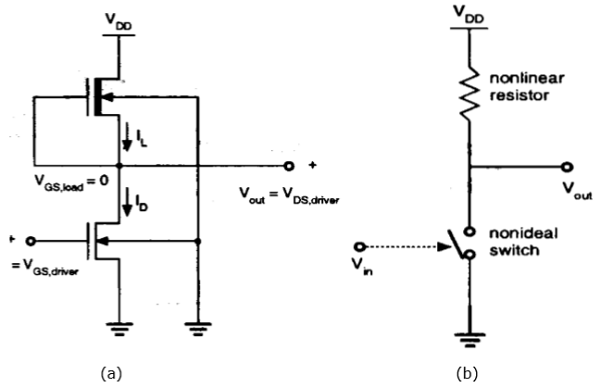
Kelemahan dari enhancement load inverter dapat diatasi dengan menggunakan depletion load inverter. Dibandingkan dengan inverter beban tambahan, inverter beban deplesi memerlukan beberapa langkah fabrikasi lagi untuk implan saluran untuk menyesuaikan tegangan ambang beban.

Keuntungan dari inverter beban penipisan adalah - transisi VTC yang tajam, margin kebisingan yang lebih baik, catu daya tunggal, dan area tata letak keseluruhan yang lebih kecil.

Seperti yang ditunjukkan pada gambar, gerbang dan terminal sumber beban dihubungkan; Jadi, V _GS = 0. Jadi, tegangan ambang beban adalah negatif. Karenanya,

$$V_{GS,load}> V_{T,load}$$ puas

Oleh karena itu, perangkat beban selalu memiliki saluran konduksi terlepas dari level tegangan input dan output.

Ketika transistor beban berada di daerah saturasi, arus beban diberikan oleh

$$I_{D,load} = \frac{K_{n,load}}{2}\left [ -V_{T,load}\left ( V_{out} \right ) \right ]^{2}$$

Ketika transistor beban berada di daerah linier, arus beban diberikan oleh

$$I_{D,load} = \frac{K_{n,load}}{2}\left [ 2\left | V_{T,load}\left ( V_{out} \right ) \right |.\left ( V_{DD}-V_{out} \right )-\left ( V_{DD}-V_{out} \right )^{2} \right ]$$

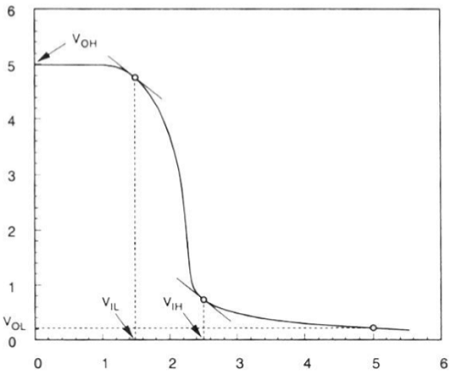
Karakteristik transfer tegangan inverter beban penipisan ditunjukkan pada gambar yang diberikan di bawah ini -

CMOS Inverter - Sirkuit, Operasi dan Deskripsi

Rangkaian inverter CMOS ditunjukkan pada gambar. Di sini, transistor nMOS dan pMOS bekerja sebagai transistor driver; ketika satu transistor ON, transistor lainnya OFF.

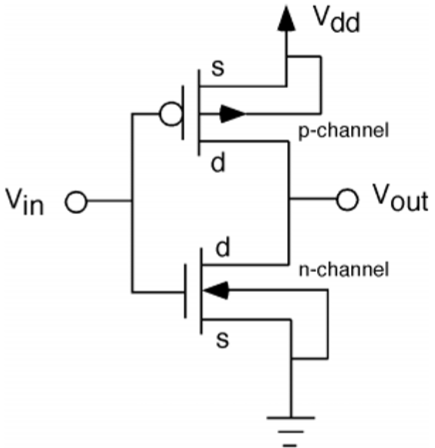
Konfigurasi ini disebut complementary MOS (CMOS). Input dihubungkan ke terminal gerbang kedua transistor sedemikian rupa sehingga keduanya dapat digerakkan langsung dengan tegangan input. Substrat nMOS disambungkan ke tanah dan substrat pMOS tersambung ke catu daya, V _DD .

Jadi V _SB = 0 untuk kedua transistor.

$$V_{GS,n}=V_{in}$$

$$V_{DS,n}=V_{out}$$

Dan,

$$V_{GS,p}=V_{in}-V_{DD}$$

$$V_{DS,p}=V_{out}-V_{DD}$$

Ketika masukan dari nMOS lebih kecil dari tegangan ambang (V _dalam <V _{TO, n} ), nMOS terputus dan pMOS berada dalam wilayah linier. Jadi, arus drain kedua transistor adalah nol.

$$I_{D,n}=I_{D,p}=0$$

Oleh karena itu, tegangan keluaran V _OH sama dengan tegangan suplai.

$$V_{out}=V_{OH}=V_{DD}$$

Ketika tegangan input lebih besar dari V _DD + V _{TO, p} , transistor pMOS berada di wilayah cutoff dan nMOS berada di wilayah linier, sehingga arus drain kedua transistor adalah nol.

$$I_{D,n}=I_{D,p}=0$$

Oleh karena itu, tegangan keluaran V _OL sama dengan nol.

$$V_{out}=V_{OL}=0$$

NMOS beroperasi di wilayah saturasi jika V _di > V _TO dan jika kondisi berikut terpenuhi.

$$V_{DS,n}\geq V_{GS,n}-V_{TO,n} $$

$$V_{out}\geq V_{in}-V_{TO,n} $$

PMOS beroperasi di wilayah saturasi jika V _di <V _DD + V _{TO, p} dan jika kondisi berikut terpenuhi.

$$V_{DS,p}\leq V_{GS,p}-V_{TO,p} $$

$$V_{out}\leq V_{in}-V_{TO,p} $$

Untuk nilai tegangan input yang berbeda, daerah operasi terdaftar di bawah untuk kedua transistor.

Wilayah	V in	V keluar	nMOS	pMOS
SEBUAH	<V TO, n	V OH	Memotong	Linear
B	V IL	Tinggi ≈ V OH	Kejenuhan	Linear
C	V th	V th	Kejenuhan	Kejenuhan
D	V IH	Rendah ≈ V OL	Linear	Kejenuhan
E	> (V DD + V TO, p )	V OL	Linear	Memotong

VTC CMOS ditunjukkan pada gambar di bawah ini -

Gerbang atau sirkuit logika kombinasional, yang melakukan operasi Boolean pada beberapa variabel masukan dan menentukan keluaran sebagai fungsi Boolean dari masukan, adalah blok bangunan dasar dari semua sistem digital. Kami akan memeriksa konfigurasi rangkaian sederhana seperti gerbang NAND dan NOR dua masukan dan kemudian memperluas analisis kami ke kasus yang lebih umum dari struktur rangkaian masukan ganda.

Selanjutnya, rangkaian logika CMOS akan disajikan dengan cara yang serupa. Kami akan menekankan persamaan dan perbedaan antara logika beban-deplesi nMOS dan sirkuit logika CMOS dan menunjukkan keuntungan gerbang CMOS dengan contoh. Dalam bentuk yang paling umum, rangkaian logika kombinasional, atau gerbang, melakukan fungsi Boolean dapat direpresentasikan sebagai sistem input ganda, output tunggal, seperti yang digambarkan pada gambar.

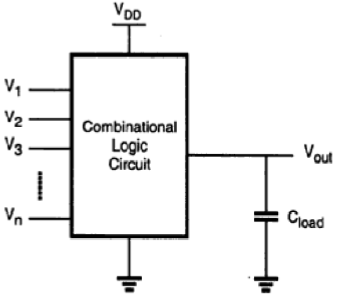
Tegangan node, yang direferensikan ke potensial ground, mewakili semua variabel input. Menggunakan konvensi logika positif, nilai Boolean (atau logika) "1" dapat diwakili oleh tegangan tinggi VDD, dan nilai Boolean (atau logika) "0" dapat diwakili oleh tegangan rendah 0. Output node dimuat dengan kapasitansi C _L , yang mewakili kapasitansi gabungan dari perangkat parasit di sirkuit.

Sirkuit Logika CMOS

CMOS Dua masukan Gerbang NOR

Sirkuit terdiri dari n-net yang terhubung paralel dan p-net komplementer yang terhubung seri. Tegangan input V _X dan V _Y diterapkan ke gerbang satu nMOS dan satu transistor pMOS.

Ketika salah satu atau kedua input tinggi, yaitu, ketika n-net membuat jalur konduksi antara node output dan tanah, p-net terputus. Jika kedua tegangan input rendah, yaitu n-net terputus, maka p-net membuat jalur konduksi antara node output dan tegangan suplai.

Untuk kombinasi masukan yang diberikan, struktur rangkaian pelengkap dibuat sedemikian rupa sehingga keluaran dihubungkan ke V _DD atau ke arde melalui jalur resistansi rendah dan jalur arus DC antara V _DD dan arde tidak dibuat untuk kombinasi masukan apa pun. Tegangan output CMOS, dua gerbang input NOR akan mendapatkan tegangan logika-rendah V _OL = 0 dan tegangan logika-tinggi V _OH = V _DD . Persamaan tegangan ambang switching V _th diberikan oleh

$$V_{th}\left ( NOR2 \right ) = \frac{V_{T,n}+\frac{1}{2}\sqrt{\frac{k_{p}}{k_{n}}\left ( V_{DD}-\left | V_{T,p} \right | \right )}}{1+\frac{1}{2}\sqrt{\frac{k_{p}}{k_{n}}}}$$

Tata letak Gerbang NOR CMOS 2-masukan

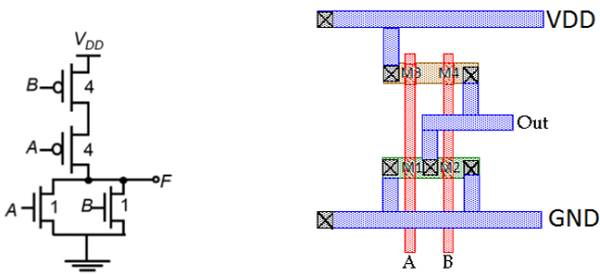
Gambar menunjukkan contoh tata letak gerbang NOR CMOS 2-masukan, menggunakan logam lapis tunggal dan polisilikon lapis tunggal. Fitur tata letak ini adalah -

• Polylines vertikal tunggal untuk setiap masukan
• Bentuk aktif tunggal untuk perangkat N dan P.
• Bus logam berjalan horizontal

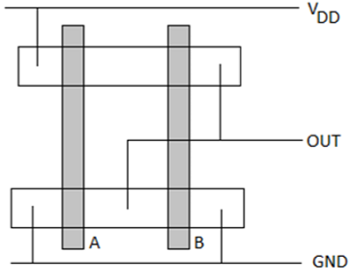
Diagram tongkat untuk gerbang CMOS N0R2 ditunjukkan pada gambar di bawah ini; yang berhubungan langsung dengan tata letak, tetapi tidak berisi informasi W dan L. Area difusi digambarkan oleh persegi panjang, sambungan logam dan garis dan lingkaran padat, masing-masing mewakili kontak, dan garis bersilang mewakili kolom polisilikon. Diagram stick berguna untuk merencanakan topologi layout yang optimal.

Gerbang NAND dua masukan CMOS

Diagram rangkaian dari dua gerbang input CMOS NAND diberikan pada gambar di bawah ini.

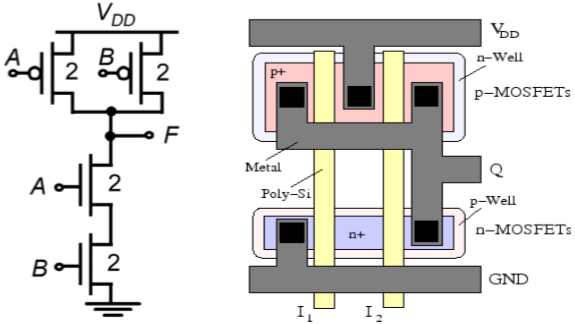
Prinsip operasi rangkaian persis ganda dari operasi CMOS dua input NOR. N - net yang terdiri dari dua seri transistor nMOS yang terhubung menciptakan jalur konduksi antara node output dan ground, jika kedua tegangan input berlogika tinggi. Kedua transistor pMOS yang terhubung paralel di p-net akan mati.

Untuk semua kombinasi input lainnya, salah satu atau kedua transistor pMOS akan ON, sedangkan p - net terputus, sehingga menciptakan jalur arus antara node output dan tegangan catu daya. Ambang pengalihan untuk gerbang ini diperoleh sebagai -

$$V_{th}\left ( NAND2 \right ) = \frac{V_{T,n}+2\sqrt{\frac{k_{p}}{k_{n}}\left ( V_{DD}-\left | V_{T,p} \right | \right )}}{1+2\sqrt{\frac{k_{p}}{k_{n}}}}$$

Fitur tata letak ini adalah sebagai berikut -

• Garis polisilikon tunggal untuk masukan berjalan secara vertikal di kedua daerah aktif N dan P.
• Bentuk aktif tunggal digunakan untuk membangun perangkat nMOS dan kedua perangkat pMOS.
• Power bussing berjalan horizontal di atas dan bawah tata letak.
• Kabel keluaran berjalan horizontal untuk memudahkan koneksi ke sirkuit tetangga.

Sirkuit Logika Kompleks

Gerbang Logika Kompleks Beban Deplesi NMOS

Untuk mewujudkan fungsi kompleks dari beberapa variabel input, struktur sirkuit dasar dan prinsip desain yang dikembangkan untuk NOR dan NAND dapat diperluas ke gerbang logika kompleks. Kemampuan untuk mewujudkan fungsi logika yang kompleks, menggunakan sejumlah kecil transistor adalah salah satu fitur paling menarik dari rangkaian logika nMOS dan CMOS. Perhatikan fungsi Boolean berikut sebagai contoh.

$$\overline{Z=P\left ( S+T \right )+QR}$$

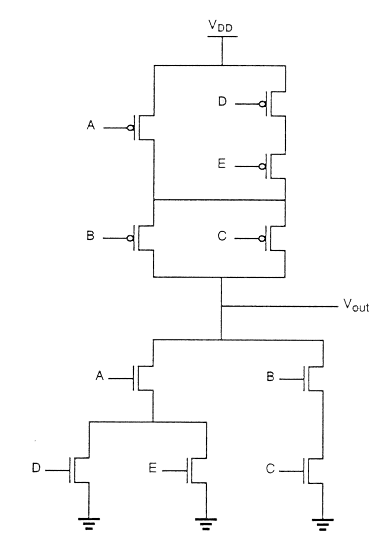
Gerbang logika kompleks deplesi-beban nMOS yang digunakan untuk mewujudkan fungsi ini ditunjukkan pada gambar. Pada gambar ini, cabang driver nMOS kiri dari tiga transistor driver digunakan untuk menjalankan fungsi logika P (S + T), sedangkan cabang sisi kanan menjalankan fungsi QR. Dengan menghubungkan kedua cabang secara paralel, dan dengan menempatkan transistor beban antara node keluaran dan tegangan suplaiV_DD,kami mendapatkan fungsi kompleks yang diberikan. Setiap variabel input ditetapkan hanya untuk satu driver.

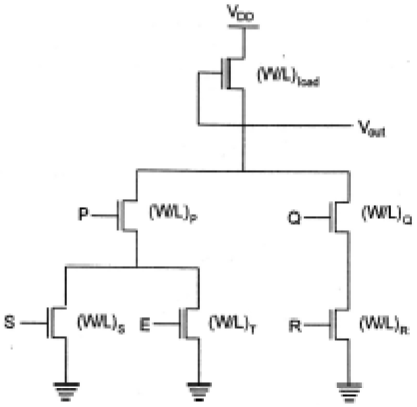
Inspeksi topologi sirkuit memberikan prinsip desain sederhana dari jaringan pull-down -

• ATAU operasi dilakukan oleh driver yang terhubung paralel.
• Operasi AND dilakukan oleh driver yang terhubung seri.
• Pembalikan disediakan oleh sifat operasi sirkuit MOS.

Jika semua variabel input logika-tinggi di sirkuit menyadari fungsinya, driver ekivalen (W/L) rasio jaringan pull-down yang terdiri dari lima transistor nMOS adalah

$$\frac{W}{L}=\frac{1}{\frac{1}{\left ( W/L \right )Q}+\frac{1}{\left ( W/L \right )R}}+\frac{1}{\frac{1}{\left ( W/L \right )P}+\frac{1}{\left ( W/L \right )S+\left ( W/L \right )Q}}$$

Gerbang Logika CMOS yang Kompleks

Realisasi jaringan n-net, atau pull-down, didasarkan pada prinsip desain dasar yang sama yang diperiksa untuk gerbang logika kompleks deplesi beban nMOS. Jaringan pull-up pMOS harus merupakan jaringan ganda dari n-net.

Artinya semua koneksi paralel di jaringan nMOS akan sesuai dengan koneksi seri di jaringan pMOS, dan semua koneksi seri di jaringan nMOS sesuai dengan koneksi paralel di jaringan pMOS. Gambar tersebut menunjukkan konstruksi sederhana grafik p-net ganda (pull-up) dari grafik n-net (pull-down).

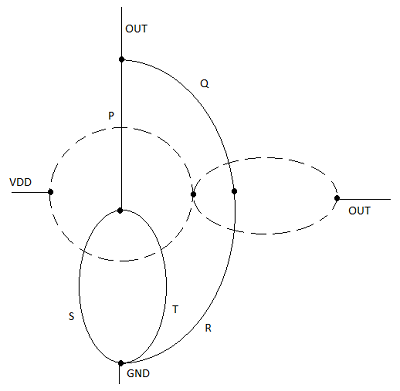
Setiap transistor driver dalam jaringan pull-down ditunjukkan oleh ai dan setiap node ditunjukkan oleh simpul pada grafik pull-down. Selanjutnya, simpul baru dibuat dalam setiap area terbatas pada grafik tarik, dan simpul tetangga dihubungkan oleh tepi yang melintasi setiap sisi pada grafik tarik-turun hanya sekali. Grafik baru ini menunjukkan jaringan pull-up.

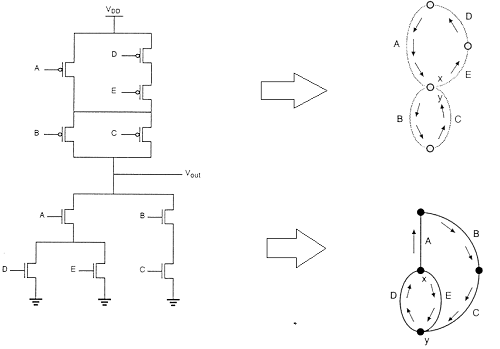
Teknik Tata Letak menggunakan Metode Graf Euler

Gambar tersebut menunjukkan implementasi CMOS dari fungsi kompleks dan diagram tongkatnya dilakukan dengan urutan gerbang arbitrer yang memberikan tata letak yang sangat tidak optimal untuk gerbang CMOS.

Dalam hal ini, pemisahan antara kolom polisilikon harus memungkinkan pemisahan difusi-untuk difusi di antaranya. Ini tentu memakan banyak area silikon ekstra.

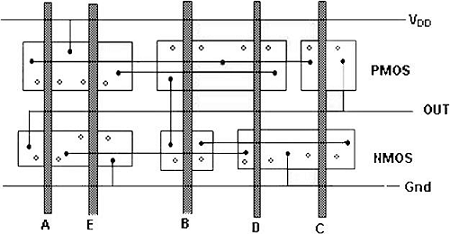
Dengan menggunakan jalur Euler, kita dapat memperoleh tata letak yang optimal. Jalur Euler didefinisikan sebagai jalur tak terputus yang melintasi setiap tepi (cabang) grafik tepat satu kali. Temukan jalur Euler di grafik pohon pull-down dan grafik pohon pull-up dengan urutan input yang identik.

Rangkaian logika dibagi menjadi dua kategori - (a) Rangkaian Kombinasional, dan (b) Rangkaian Sekuensial.

Dalam rangkaian kombinasional, keluaran hanya bergantung pada kondisi masukan terakhir.

Dalam rangkaian sekuensial, keluaran tidak hanya bergantung pada masukan terbaru, tetapi juga kondisi masukan sebelumnya. Sirkuit sekuensial mengandung elemen memori.

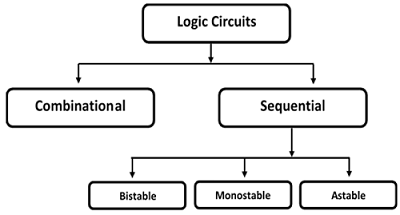
Rangkaian sekuensial terdiri dari tiga jenis -

Bistable- Sirkuit Bistable memiliki dua titik operasi yang stabil dan akan berada di salah satu status. Contoh - Sel memori, kait, sandal jepit, dan register.

Monostable- Sirkuit monostabil hanya memiliki satu titik operasi stabil dan bahkan jika untuk sementara diganggu ke keadaan sebaliknya, mereka akan kembali pada waktunya ke titik operasi stabilnya. Contoh: Timer, generator pulsa.

Astable- sirkuit tidak memiliki titik operasi yang stabil dan berosilasi di antara beberapa keadaan. Contoh - Cincin osilator.

Sirkuit Logika CMOS

SR Latch berdasarkan NOR Gate

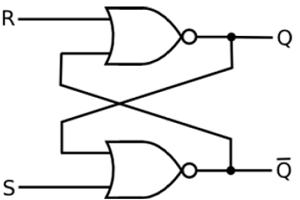
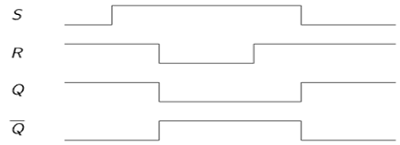
Jika set input (S) sama dengan logika "1" dan input reset sama dengan logika "0." maka output Q akan dipaksa ke logika "1". Sementara$\overline{Q}$ dipaksa untuk logika "0". Ini berarti pengunci SR akan disetel, terlepas dari status sebelumnya.

Demikian pula, jika S sama dengan "0" dan R sama dengan "1" maka output Q akan dipaksa "0" sementara $\overline{Q}$ dipaksa untuk "1". Ini berarti kait disetel ulang, terlepas dari status dipegang sebelumnya. Akhirnya, jika kedua input S dan R sama dengan logika"1" maka kedua keluaran akan dipaksa ke logika "0" yang bertentangan dengan komplementaritas Q dan $\overline{Q}$.

Oleh karena itu, kombinasi input ini tidak diperbolehkan selama pengoperasian normal. Tabel kebenaran SR Latch berbasis NOR diberikan dalam tabel.

S	R	Q	$\overline{Q}$	Operasi
0	0	Q	$\overline{Q}$	Memegang
1	0	1	0	Set
0	1	0	1	Setel ulang
1	1	0	0	Tidak diperbolehkan

Kait CMOS SR berdasarkan gerbang NOR ditunjukkan pada gambar di bawah ini.

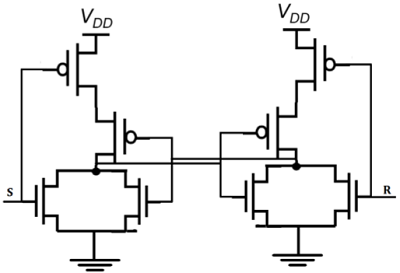
Jika S sama dengan V _OH dan R sama dengan V _OL , kedua transistor yang terhubung paralel M1 dan M2 akan ON. Tegangan pada node$\overline{Q}$akan mengasumsikan tingkat logika rendah V _OL = 0.

Pada saat yang sama, M3 dan M4 dimatikan, yang menghasilkan tegangan logika-tinggi V _OH pada node Q. Jika R sama dengan V _OH dan S sama dengan V _OL , M1 dan M2 dimatikan dan M3 dan M4 dihidupkan.

SR Latch berdasarkan NAND Gate

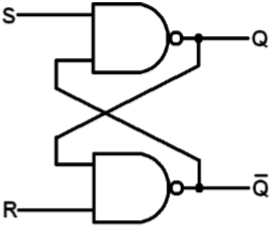
Diagram blok dan skema level gerbang kait SR berbasis NAND ditunjukkan pada gambar. Lingkaran kecil di terminal input S dan R menunjukkan bahwa rangkaian tersebut merespons sinyal input rendah yang aktif. Tabel kebenaran kait SR berbasis NAND diberikan dalam tabel

S	R	Q	Q ′
0	0	NC	NC	Tidak ada perubahan. Latch tetap dalam kondisi sekarang.
1	0	1	0	SET Kancing.
0	1	0	1	Latch RESET.
1	1	0	0	Kondisi tidak valid.

Jika S pergi ke 0 (sementara R = 1), Q pergi tinggi, menarik $\overline{Q}$ rendah dan kait memasuki kondisi Set

S = 0 lalu Q = 1 (jika R = 1)

Jika R pergi ke 0 (sementara S = 1), Q pergi tinggi, menarik $\overline{Q}$ rendah dan kaitnya disetel ulang

R = 0 lalu Q = 1 (jika S = 1)

Status tahan mengharuskan S dan R menjadi tinggi. Jika S = R = 0 maka keluaran tidak diperbolehkan, karena akan menghasilkan keadaan tak tentu. CMOS SR Latch berdasarkan NAND Gate ditunjukkan pada gambar.

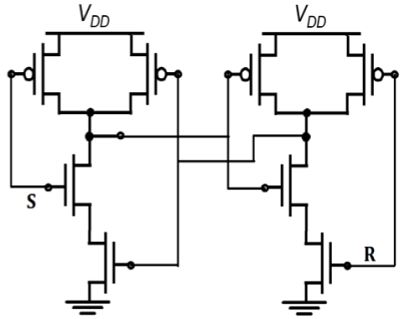
Deplesi-load nMOS SR Latch berdasarkan NAND Gate ditunjukkan pada gambar. Pengoperasiannya mirip dengan kait CMOS NAND SR. Implementasi sirkuit CMOS memiliki disipasi daya statis yang rendah dan margin noise yang tinggi.

Sirkuit Logika CMOS

SR Latch Clocked

Gambar menunjukkan kait SR berbasis NOR dengan jam yang ditambahkan. Latch responsif terhadap input S dan R hanya jika CLK tinggi.

Saat CLK rendah, kait mempertahankan statusnya saat ini. Perhatikan bahwa Q berubah status -

• Ketika S menjadi tinggi selama CLK positif.
• Di tepi CLK terdepan setelah perubahan S & R selama waktu rendah CLK.
• Kesalahan positif di S sementara CLK tinggi
• Ketika R menjadi tinggi selama CLK positif.

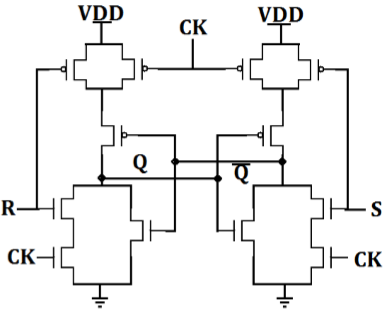
Implementasi CMOS AOI dari kait SR berbasis NOR clocked ditunjukkan pada gambar. Perhatikan bahwa hanya 12 transistor yang dibutuhkan.

• Ketika CLK rendah, dua terminal seri di N pohon N terbuka dan dua transistor paralel di pohon P ON, sehingga mempertahankan status dalam sel memori.

• Ketika clock tinggi, rangkaian hanya menjadi kait CMOS berbasis NOR yang akan merespons input S dan R.

Clocked SR Latch based on NAND Gate

Sirkuit diimplementasikan dengan empat gerbang NAND. Jika rangkaian ini diimplementasikan dengan CMOS maka membutuhkan 16 transistor.

• Latch responsif terhadap S atau R hanya jika CLK tinggi.
• Jika kedua sinyal masukan dan sinyal CLK aktif tinggi: yaitu, keluaran kait Q akan disetel saat CLK = "1" S = "1" dan R = "0"
• Demikian pula, kait akan disetel ulang saat CLK = "1," S = "0," dan

Saat CLK rendah, kait mempertahankan keadaannya saat ini.

Jam JK Latch

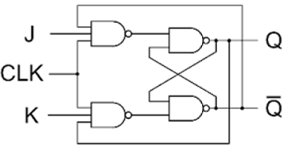
Gambar di atas menunjukkan kait JK dengan clock, berdasarkan gerbang NAND. Kerugian dari SR latch adalah ketika S dan R sama-sama tinggi, status keluarannya menjadi tidak pasti. Kait JK menghilangkan masalah ini dengan menggunakan umpan balik dari keluaran ke masukan, sehingga semua status masukan dari tabel kebenaran diperbolehkan. Jika J = K = 0, kait akan menahan keadaannya saat ini.

Jika J = 1 dan K = 0, pengunci akan dipasang pada sisi jam berjalan positif berikutnya, yaitu Q = 1, $\overline{Q}$ = 0

Jika J = 0 dan K = 1, kait akan direset pada tepi jam berjalan positif berikutnya, yaitu Q = 1 dan $\overline{Q}$ = 0.

Jika J = K = 1, pengunci akan beralih ke tepi jam berjalan positif berikutnya

Pengoperasian latch JK clock diringkas dalam tabel kebenaran yang diberikan dalam tabel.

J	K	Q	$\overline{Q}$	S	R	Q	$\overline{Q}$	Operation
0	0	0	1	1	1	0	1	Memegang
		1	0	1	1	1	0
0	1	0	1	1	1	0	1	Setel ulang
		1	0	1	0	0	1
1	0	0	1	0	1	1	0	Set
		1	0	1	1	1	0
1	1	0	1	0	1	1	0	beralih
		1	0	1	0	0	1

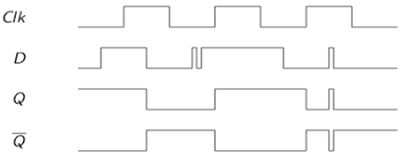
Implementasi CMOS D Latch

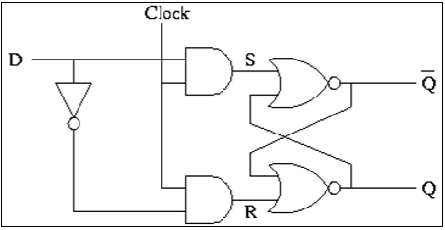
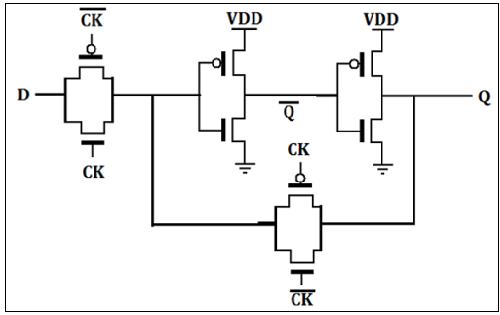
Kait D biasanya, diimplementasikan dengan sakelar gerbang transmisi (TG) seperti yang ditunjukkan pada gambar. TG input diaktifkan dengan CLK sementara TG loop umpan balik kait diaktifkan dengan CLK. Input D diterima saat CLK tinggi. Ketika CLK menjadi rendah, input disirkulasikan terbuka dan kait diatur dengan data D.

VHDL adalah singkatan dari bahasa deskripsi perangkat keras sirkuit terintegrasi berkecepatan sangat tinggi. Ini adalah bahasa pemrograman yang digunakan untuk memodelkan sistem digital dengan aliran data, gaya pemodelan perilaku dan struktural. Bahasa ini pertama kali diperkenalkan pada tahun 1981 untuk departemen Pertahanan (DoD) di bawah program VHSIC.

Menjelaskan Desain

Dalam VHDL, entitas digunakan untuk mendeskripsikan modul perangkat keras. Suatu entitas dapat dijelaskan menggunakan,

• Deklarasi entitas
• Architecture
• Configuration
• Deklarasi paket
• Isi paket

Mari kita lihat apa ini?

Deklarasi Entitas

Ini mendefinisikan nama, sinyal input output dan mode modul perangkat keras.

Syntax -

entity entity_name is
   Port declaration;
end entity_name;

Deklarasi entitas harus dimulai dengan 'entitas' dan diakhiri dengan kata kunci 'akhir'. Arahnya akan menjadi input, output atau inout.

Di	Port bisa dibaca
Di luar	Port dapat ditulis
Masuk	Port dapat dibaca dan ditulis
Penyangga	Port dapat dibaca dan ditulis, hanya dapat memiliki satu sumber.

Architecture -

Arsitektur dapat dideskripsikan menggunakan struktur, aliran data, perilaku atau gaya campuran.

Syntax -

architecture architecture_name of entity_name 
architecture_declarative_part;

begin
   Statements;
end architecture_name;

Di sini, kita harus menentukan nama entitas yang akan kita tuliskan badan arsitekturnya. Pernyataan arsitektur harus berada di dalam kata kunci 'begin' dan 'énd'. Bagian deklaratif arsitektur dapat berisi variabel, konstanta, atau deklarasi komponen.

Pemodelan Arus Data

Dalam gaya pemodelan ini, aliran data melalui entitas diekspresikan menggunakan sinyal konkuren (paralel). Pernyataan serentak di VHDL adalah WHEN dan GENERATE.

Selain itu, tugas yang hanya menggunakan operator (AND, NOT, +, *, sll, dll.) Juga dapat digunakan untuk membuat kode.

Terakhir, jenis tugas khusus, yang disebut BLOK, juga dapat digunakan dalam kode jenis ini.

Dalam kode bersamaan, berikut ini dapat digunakan -

• Operators
• Pernyataan WHEN (WHEN / ELSE atau WITH / SELECT / WHEN);
• Pernyataan GENERATE;
• Pernyataan BLOK

Pemodelan Perilaku

Dalam gaya pemodelan ini, perilaku entitas sebagai kumpulan pernyataan dijalankan secara berurutan dalam urutan yang ditentukan. Hanya pernyataan yang ditempatkan di dalam PROCESS, FUNCTION, atau PROCEDURE yang berurutan.

PROSES, FUNGSI, dan PROSEDUR adalah satu-satunya bagian kode yang dieksekusi secara berurutan.

Namun, secara keseluruhan, salah satu blok ini masih bersamaan dengan pernyataan lain yang ditempatkan di luarnya.

Satu aspek penting dari kode perilaku adalah tidak terbatas pada logika sekuensial. Memang, dengan itu, kita dapat membangun rangkaian sekuensial maupun rangkaian kombinasional.

Pernyataan perilaku adalah IF, WAIT, CASE, dan LOOP. VARIABEL juga dibatasi dan hanya digunakan dalam kode berurutan. VARIABEL tidak pernah bisa mendunia, jadi nilainya tidak bisa langsung disalurkan.

Pemodelan Struktural

Dalam pemodelan ini, entitas digambarkan sebagai sekumpulan komponen yang saling berhubungan. Pernyataan instansiasi komponen adalah pernyataan bersamaan. Oleh karena itu, urutan pernyataan ini tidak penting. Gaya pemodelan struktural hanya menggambarkan interkoneksi komponen (dilihat sebagai kotak hitam), tanpa menyiratkan perilaku komponen itu sendiri maupun entitas yang mereka wakili secara kolektif.

Dalam pemodelan struktural, badan arsitektur terdiri dari dua bagian - bagian deklaratif (sebelum kata kunci dimulai) dan bagian pernyataan (setelah kata kunci dimulai).

Operasi Logika - DAN GERBANG

X	Y	Z
0	0	0
0	1	0
1	0	0
1	1	1

VHDL Code:
Library ieee;
use ieee.std_logic_1164.all;

entity and1 is
   port(x,y:in bit ; z:out bit);
end and1;

architecture virat of and1 is
begin
   z<=x and y; 
end virat;

Bentuk gelombang

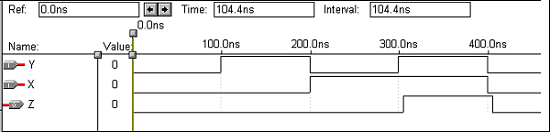
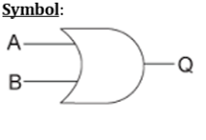
Operasi Logika - OR Gerbang

X	Y	Z
0	0	0
0	1	1
1	0	1
1	1	1

VHDL Code: 
Library ieee; 
use ieee.std_logic_1164.all;  

entity or1 is
   port(x,y:in bit ; z:out bit); 
end or1; 
 
architecture virat of or1 is
begin
   z<=x or y; 
end virat;

Bentuk gelombang

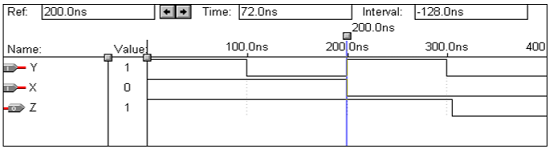
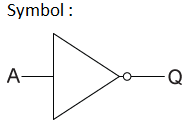
Operasi Logika - BUKAN Gerbang

X	Y
0	1
1	0

VHDL Code:
  
Library ieee; 
use ieee.std_logic_1164.all; 
 
entity not1 is
   port(x:in bit ; y:out bit); 
end not1; 
 
architecture virat of not1 is
begin
   y<=not x;
end virat;

Bentuk gelombang

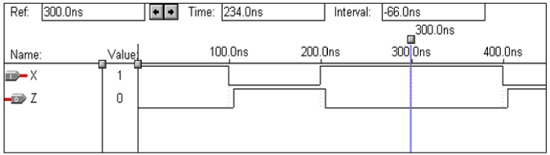
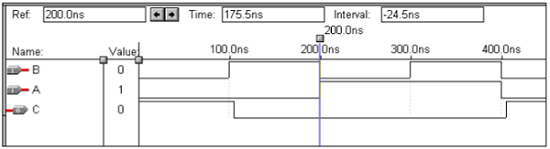
Operasi Logika - Gerbang NAND

X	Y	z
0	0	1
0	1	1
1	0	1
1	1	0

VHDL Code:
  
Library ieee; 
use ieee.std_logic_1164.all; 

entity nand1 is
   port(a,b:in bit ; c:out bit); 
end nand1; 
 
architecture virat of nand1 is
begin
   c<=a nand b; 
end virat;

Bentuk gelombang

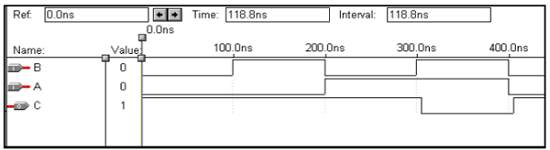
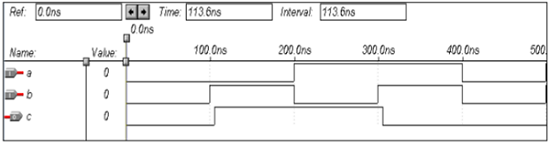
Operasi Logika - Gerbang NOR

X	Y	z
0	0	1
0	1	0
1	0	0
1	1	0

VHDL Code: 
 
Library ieee; 
use ieee.std_logic_1164.all; 
 
entity nor1 is
   port(a,b:in bit ; c:out bit); 
end nor1; 
 
architecture virat of nor1 is
begin
   c<=a nor b;
end virat;

Bentuk gelombang

Operasi Logika - Gerbang XOR

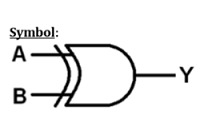
X	Y	Z
0	0	1
0	1	1
1	0	1
1	1	0

VHDL Code: 
 
Library ieee; 
use ieee.std_logic_1164.all;
  
entity xor1 is
   port(a,b:in bit ; c:out bit); 
end xor1;
  
architecture virat of xor1 is
begin
   c<=a xor b; 
end virat;

Bentuk gelombang

Operasi Logika - Gerbang X-NOR

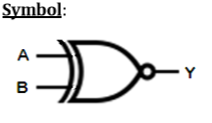
X	Y	Z
0	0	1
0	1	1
1	0	1
1	1	0

VHDL Code: 
 
Library ieee; 
use ieee.std_logic_1164.all; 

entity xnor1 is
   port(a,b:in bit ; c:out bit); 
end xnor1; 
 
architecture virat of xnor1 is
begin
   c<=not(a xor b); 
end virat;

Bentuk gelombang

Bab ini menjelaskan pemrograman VHDL untuk Sirkuit Kombinasional.

Kode VHDL untuk Half-Adder

VHDL Code:
  
Library ieee; 
use ieee.std_logic_1164.all;
  
entity half_adder is
   port(a,b:in bit; sum,carry:out bit); 
end half_adder; 
 
architecture data of half_adder is
begin
   sum<= a xor b;  
   carry <= a and b;  
end data;

Bentuk gelombang

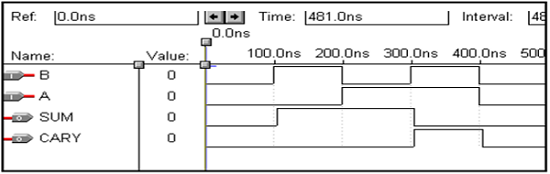
Kode VHDL untuk Full Adder

Library ieee; 
use ieee.std_logic_1164.all;
 
entity full_adder is port(a,b,c:in bit; sum,carry:out bit); 
end full_adder;
  
architecture data of full_adder is
begin
   sum<= a xor b xor c; 
   carry <= ((a and b) or (b and c) or (a and c)); 
end data;

Bentuk gelombang

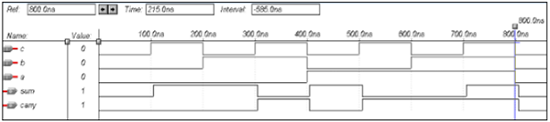
Kode VHDL untuk Pengurang Setengah

Library ieee;
use ieee.std_logic_1164.all;
  
entity half_sub is
   port(a,c:in bit; d,b:out bit);
end half_sub;  

architecture data of half_sub is
begin
   d<= a xor c;
   b<= (a and (not c));
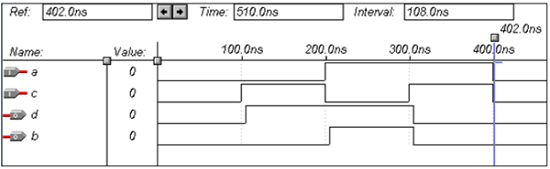
end data;

Bentuk gelombang

Kode VHDL untuk Pengurang Penuh

Library ieee; 
use ieee.std_logic_1164.all;
  
entity full_sub is
   port(a,b,c:in bit; sub,borrow:out bit); 
end full_sub; 
 
architecture data of full_sub is
begin
   sub<= a xor b xor c; 
   borrow <= ((b xor c) and (not a)) or (b and c); 
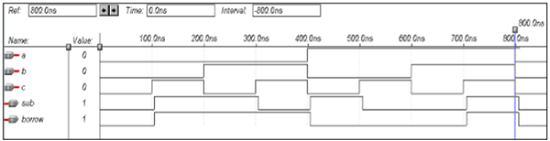
end data;

Bentuk gelombang

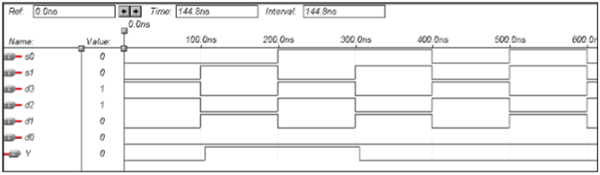
Kode VHDL untuk Multiplexer

Library ieee; 
use ieee.std_logic_1164.all;
  
entity mux is
   port(S1,S0,D0,D1,D2,D3:in bit; Y:out bit);
end mux;
  
architecture data of mux is
begin 
   Y<= (not S0 and not S1 and D0) or 
      (S0 and not S1 and D1) or 
      (not S0 and S1 and D2) or
      (S0 and S1 and D3); 
end data;

Bentuk gelombang

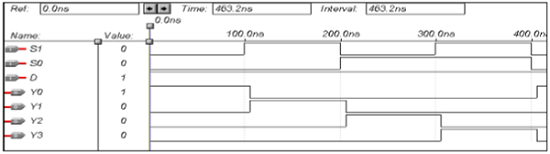
Kode VHDL untuk Demultiplexer

Library ieee; 
use ieee.std_logic_1164.all;
  
entity demux is
   port(S1,S0,D:in bit; Y0,Y1,Y2,Y3:out bit); 
end demux;
  
architecture data of demux is
begin 
   Y0<=  ((Not S0) and (Not S1) and D); 
   Y1<=  ((Not S0) and S1 and D); 
   Y2<=  (S0 and (Not S1) and D); 
   Y3<=  (S0 and S1 and D); 
end data;

Bentuk gelombang

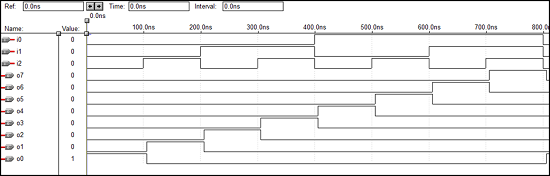
Kode VHDL untuk Encoder 8 x 3

library ieee; 
use ieee.std_logic_1164.all; 
 
entity enc is
   port(i0,i1,i2,i3,i4,i5,i6,i7:in bit; o0,o1,o2: out bit); 
end enc; 
 
architecture vcgandhi of enc is
begin 
   o0<=i4 or i5 or i6 or i7; 
   o1<=i2 or i3 or i6 or i7; 
   o2<=i1 or i3 or i5 or i7; 
end vcgandhi;

Bentuk gelombang

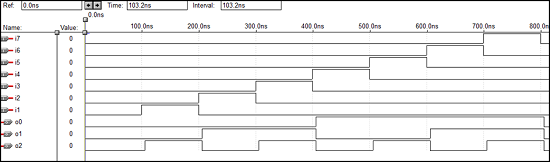
Kode VHDL untuk Decoder 3 x 8

library ieee; 
use ieee.std_logic_1164.all;

entity dec is
   port(i0,i1,i2:in bit; o0,o1,o2,o3,o4,o5,o6,o7: out bit); 
end dec; 
 
architecture vcgandhi of dec is
begin 
   o0<=(not i0) and (not i1) and (not i2); 
   o1<=(not i0) and (not i1) and i2; 
   o2<=(not i0) and i1 and (not i2); 
   o3<=(not i0) and i1 and i2; 
   o4<=i0 and (not i1) and (not i2); 
   o5<=i0 and (not i1) and i2; 
   o6<=i0 and i1 and (not i2); 
   o7<=i0 and i1 and i2; 
end vcgandhi;

Bentuk gelombang

Kode VHDL - Penambah paralel 4 bit

library IEEE; 
use IEEE.STD_LOGIC_1164.all;
  
entity pa is
   port(a : in STD_LOGIC_VECTOR(3 downto 0);
      b : in STD_LOGIC_VECTOR(3 downto 0);
      ca : out STD_LOGIC;
      sum : out STD_LOGIC_VECTOR(3 downto 0) 
   ); 
end pa; 
 
architecture vcgandhi of pa is
   Component fa is
      port (a : in STD_LOGIC; 
         b : in STD_LOGIC; 
         c : in STD_LOGIC; 
         sum : out STD_LOGIC; 
         ca : out STD_LOGIC
      ); 
   end component;         
   signal s : std_logic_vector (2 downto 0); 
   signal temp: std_logic;
begin 
   temp<='0'; 
   u0 : fa port map (a(0),b(0),temp,sum(0),s(0)); 
   u1 : fa port map (a(1),b(1),s(0),sum(1),s(1)); 
   u2 : fa port map (a(2),b(2),s(1),sum(2),s(2));
   ue : fa port map (a(3),b(3),s(2),sum(3),ca);  
end vcgandhi;

Bentuk gelombang

Kode VHDL - Pemeriksa Paritas 4 bit

library ieee; 
use ieee.std_logic_1164.all; 
 
entity parity_checker is 
   port (a0,a1,a2,a3 : in std_logic; 
      p : out std_logic); 
end parity_checker;  

architecture vcgandhi of parity_checker is 
begin    
   p <= (((a0 xor a1) xor a2) xor a3); 
end vcgandhi;

Bentuk gelombang

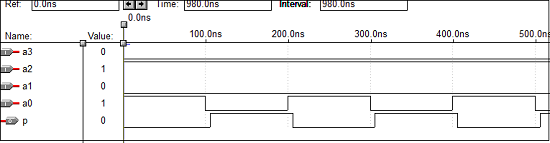
Kode VHDL - Generator Paritas 4 bit

library ieee;
use ieee.std_logic_1164.all;

entity paritygen is
   port (a0, a1, a2, a3: in std_logic; p_odd, p_even: out std_logic);
end paritygen;  

architecture vcgandhi of paritygen is
begin
   process (a0, a1, a2, a3)
   
	if (a0 ='0' and a1 ='0' and a2 ='0' and a3 =’0’)
      then odd_out <= "0";
      even_out <= "0";
   else
      p_odd <= (((a0 xor a1) xor a2) xor a3);
      p_even <= not(((a0 xor a1) xor a2) xor a3);  
end vcgandhi

Bentuk gelombang

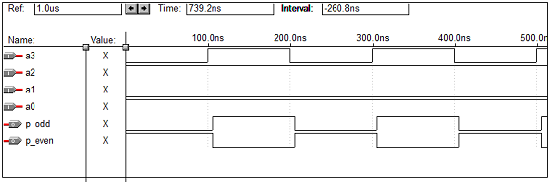
Bab ini menjelaskan cara melakukan pemrograman VHDL untuk Rangkaian Sekuensial.

Kode VHDL untuk SR Latch

library ieee; 
use ieee.std_logic_1164.all;
  
entity srl is 
   port(r,s:in bit; q,qbar:buffer bit); 
end srl;  

architecture virat of srl is 
   signal s1,r1:bit; 
begin 
   q<= s nand qbar; 
   qbar<= r nand q; 
end virat;

Bentuk gelombang

Kode VHDL untuk D Latch

library ieee; 
use ieee.std_logic_1164.all;

entity Dl is 
   port(d:in bit; q,qbar:buffer bit); 
end Dl; 
 
architecture virat of Dl is 
   signal s1,r1:bit; 
begin 
   q<= d nand qbar; 
   qbar<= d nand q; 
end virat;

Bentuk gelombang

Kode VHDL untuk SR Flip Flop

library ieee; 
use ieee.std_logic_1164.all;
  
entity srflip is 
   port(r,s,clk:in bit; q,qbar:buffer bit); 
end srflip;
  
architecture virat of srflip is 
   signal s1,r1:bit; 
begin 
   s1<=s nand clk; 
   r1<=r nand clk;
   q<= s1 nand qbar;
   qbar<= r1 nand q;
end virat;

Bentuk gelombang

Kode VHDL untuk JK Flip Flop

library IEEE; 
use IEEE.STD_LOGIC_1164.all;  

entity jk is 
   port(
      j : in STD_LOGIC; 
      k : in STD_LOGIC; 
      clk : in STD_LOGIC; 
      reset : in STD_LOGIC; 
      q : out STD_LOGIC; 
      qb : out STD_LOGIC 
   ); 
end jk;
  
architecture virat of jk is 
begin 
   jkff : process (j,k,clk,reset) is 
   variable m : std_logic := '0'; 
   
   begin 
      if (reset = '1') then 
         m : = '0'; 
      elsif (rising_edge (clk)) then 
         if (j/ = k) then
            m : = j; 
         elsif (j = '1' and k = '1') then 
            m : = not m; 
         end if; 
      end if; 
      
      q <= m; 
      qb <= not m; 
   end process jkff; 
end virat;

Bentuk gelombang

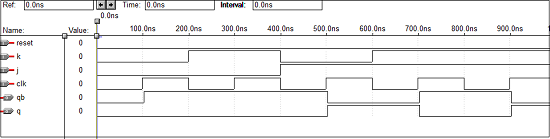
Kode VHDL untuk D Flip Flop

Library ieee; 
use ieee.std_logic_1164.all;  

entity dflip is 
   port(d,clk:in bit; q,qbar:buffer bit); 
end dflip; 
 
architecture virat of dflip is 
   signal d1,d2:bit; 
begin 
   d1<=d nand clk; 
   d2<=(not d) nand clk; 
   q<= d1 nand qbar; 
   qbar<= d2 nand q; 
end virat;

Bentuk gelombang

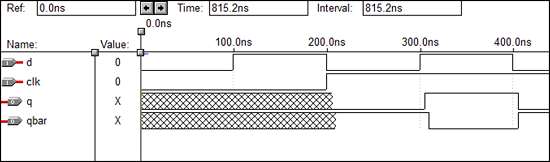
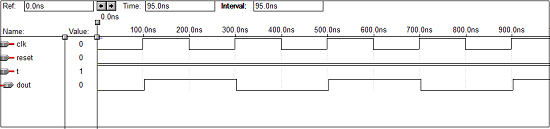
Kode VHDL untuk T Flip Flop

library IEEE; 
use IEEE.STD_LOGIC_1164.all;  

entity Toggle_flip_flop is 
   port( 
      t : in STD_LOGIC; 
      clk : in STD_LOGIC; 
      reset : in STD_LOGIC; 
      dout : out STD_LOGIC
   ); 
end Toggle_flip_flop;  

architecture virat of Toggle_flip_flop is 
begin 
   tff : process (t,clk,reset) is 
   variable m : std_logic : = '0'; 
   
   begin 
      if (reset = '1') then 
         m : = '0'; 
      elsif (rising_edge (clk)) then 
         if (t = '1') then 
            m : = not m;        
         end if; 
      end if; 
      dout < = m; 
   end process tff; 
end virat;

Bentuk gelombang

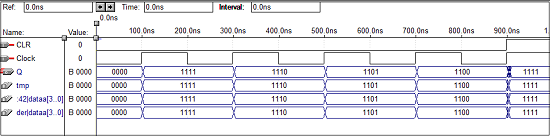
Kode VHDL untuk Penghitung 4-bit

library IEEE; 
use ieee.std_logic_1164.all; 
use ieee.std_logic_unsigned.all;
  
entity counter is 
   port(Clock, CLR : in std_logic; 
      Q : out std_logic_vector(3 downto 0)
   ); 
end counter;  

architecture virat of counter is 
   signal tmp: std_logic_vector(3 downto 0); 
begin 
   process (Clock, CLR) 
   
   begin 
      if (CLR = '1') then 
         tmp < = "0000"; 
      elsif (Clock'event and Clock = '1') then 
         mp <= tmp + 1; 
      end if; 
   end process; 
   Q <= tmp; 
end virat;

Bentuk gelombang

Kode VHDL untuk Penghitung Bawah 4-bit

library ieee; 
use ieee.std_logic_1164.all; 
use ieee.std_logic_unsigned.all;
  
entity dcounter is 
   port(Clock, CLR : in std_logic; 
      Q : out std_logic_vector(3 downto 0)); 
end dcounter; 
 
architecture virat of dcounter is 
   signal tmp: std_logic_vector(3 downto 0); 

begin 
   process (Clock, CLR) 
   begin 
      if (CLR = '1') then 
         tmp <= "1111"; 
      elsif (Clock'event and Clock = '1') then 
         tmp <= tmp - 1; 
      end if; 
   end process; 
   Q <= tmp; 
end virat;

Bentuk gelombang

Verilog adalah HARDWARE DESCRIPTION LANGUAGE (HDL). Ini adalah bahasa yang digunakan untuk menjelaskan sistem digital seperti sakelar jaringan atau mikroprosesor atau memori atau flip-flop. Artinya, dengan menggunakan HDL kami dapat mendeskripsikan perangkat keras digital apa pun di tingkat mana pun. Desain, yang dijelaskan dalam HDL tidak bergantung pada teknologi, sangat mudah untuk mendesain dan men-debug, dan biasanya lebih berguna daripada skema, terutama untuk sirkuit besar.

Verilog mendukung desain di berbagai tingkat abstraksi. Tiga utama adalah -

• Tingkat perilaku
• Tingkat pendaftaran-transfer
• Tingkat gerbang

Tingkat perilaku

Level ini menggambarkan sistem dengan algoritma konkuren (Behavioral). Setiap algoritme bersifat sekuensial, artinya terdiri dari sekumpulan instruksi yang dijalankan satu per satu. Fungsi, tugas, dan blok adalah elemen utama. Tidak ada perhatian pada realisasi struktural desain.

Daftar − Tingkat Transfer

Desain menggunakan Register − Transfer Level menentukan karakteristik rangkaian yang menggunakan operasi dan transfer data antar register. Definisi modern dari kode RTL adalah "Setiap kode yang dapat disintesis disebut kode RTL".

Level Gerbang

Dalam tingkat logika, karakteristik suatu sistem dijelaskan oleh tautan logis dan properti waktunya. Semua sinyal adalah sinyal diskrit. Mereka hanya dapat memiliki nilai logika yang pasti (`0 ',` 1', `X ',` Z`). Operasi yang dapat digunakan adalah logika primitif yang telah ditentukan sebelumnya (gerbang dasar). Pemodelan level gerbang mungkin bukan ide yang tepat untuk desain logika. Kode level gerbang dibuat menggunakan alat-alat seperti alat sintesis dan netlist-nya digunakan untuk simulasi level gerbang dan untuk backend.

Token Leksikal

File teks sumber bahasa Verilog adalah aliran token leksikal. Token terdiri dari satu atau lebih karakter, dan setiap karakter berada tepat di satu token.

Token leksikal dasar yang digunakan oleh Verilog HDL mirip dengan yang ada di Bahasa Pemrograman C. Verilog peka huruf besar / kecil. Semua kata kunci menggunakan huruf kecil.

Ruang Putih

Spasi putih dapat berisi karakter untuk spasi, tab, baris baru, dan umpan formulir. Karakter ini diabaikan kecuali jika berfungsi untuk memisahkan token.

Karakter spasi putih adalah Ruang kosong, Tab, Pengembalian kereta, Baris baru, dan Umpan formulir.

Komentar

Ada dua bentuk untuk mewakili komentar tersebut

• 1) Komentar baris tunggal dimulai dengan token // dan diakhiri dengan carriage return.

Mis .: // ini adalah sintaks baris tunggal

• 2) Komentar multiline dimulai dengan token / * dan diakhiri dengan token * /

Mis .: / * ini adalah Sintaks multiline * /

Angka

Anda dapat menentukan angka dalam format biner, oktal, desimal, atau heksadesimal. Angka negatif diwakili dalam angka pujian 2. Verilog memungkinkan bilangan bulat, bilangan real dan bilangan bertanda & tak bertanda tangan.

Sintaksnya diberikan oleh - <size> <radix> <value>

Ukuran atau bilangan unsized dapat ditentukan dalam <Size> dan <radix> menentukan apakah itu biner, oktal, heksadesimal atau desimal.

Pengenal

Identifier adalah nama yang digunakan untuk mendefinisikan objek, seperti fungsi, modul atau register. Pengenal harus dimulai dengan karakter alfabet atau karakter garis bawah. Ex. A_Z, a_z, _

Pengidentifikasi adalah kombinasi dari karakter alfabet, numerik, garis bawah, dan $. Panjangnya bisa sampai 1024 karakter.

Operator

Operator adalah karakter khusus yang digunakan untuk meletakkan kondisi atau mengoperasikan variabel. Ada satu, dua, dan terkadang tiga karakter yang digunakan untuk melakukan operasi pada variabel.

Ex. >, +, ~, &! =.

Kata Kunci Verilog

Kata-kata yang memiliki arti khusus di Verilog disebut kata kunci Verilog. Misalnya assign, case, while, wire, reg, and, or, nand, dan module. Mereka tidak boleh digunakan sebagai pengenal. Kata kunci Verilog juga menyertakan arahan kompiler, serta tugas dan fungsi sistem.

Pemodelan Level Gerbang

Verilog memiliki primitif bawaan seperti gerbang logika, gerbang transmisi, dan sakelar. Ini jarang digunakan untuk pekerjaan desain tetapi mereka digunakan di dunia pasca sintesis untuk pemodelan sel ASIC / FPGA.

Pemodelan tingkat gerbang menunjukkan dua properti -

Drive strength- Kekuatan gerbang keluaran ditentukan oleh kekuatan penggerak. Output terkuat jika ada koneksi langsung ke sumbernya. Kekuatan berkurang jika koneksi melalui transistor konduksi dan paling sedikit ketika terhubung melalui resistif pull-up / down. Kekuatan drive biasanya tidak ditentukan, dalam hal ini kekuatan defaultnya adalah strong1 dan strong0.

Delays- Jika penundaan tidak ditentukan, maka gerbang tidak memiliki penundaan propagasi; jika dua penundaan ditentukan, maka yang pertama mewakili penundaan naik dan yang kedua, penundaan jatuh; jika hanya satu penundaan yang ditentukan, maka naik dan turun keduanya sama. Penundaan dapat diabaikan dalam sintesis.

Gerbang Primitif

Gerbang logika dasar menggunakan satu keluaran dan banyak masukan digunakan di Verilog. GATE menggunakan salah satu kata kunci - dan, nand, atau, nor, xor, xnor untuk digunakan di Verilog untuk jumlah N masukan dan 1 keluaran.

Example:  
   Module gate() 
   Wire ot0; 
   Wire ot1; 
   Wire ot2; 
   
   Reg in0,in1,in2,in3; 
   Not U1(ot0,in0); 
   Xor U2(ot1,in1,in2,in3); 
   And U3(ot2, in2,in3,in0)

Primitif Gerbang Transmisi

Primitif gerbang transmisi mencakup keduanya, buffer dan inverter. Mereka memiliki masukan tunggal dan satu atau lebih keluaran. Dalam sintaks instantiasi gerbang yang ditunjukkan di bawah ini, GATE adalah singkatan dari kata kunci buf atau gerbang NOT.

Contoh: Not, buf, bufif0, bufif1, notif0, notif1

Bukan - n inverter outout

Buf - penyangga keluaran

Bufifo - buffer tristate, aktif rendah aktif

Bufif1 - buffer tristate, aktif tinggi aktif

Notifo - inverter tristate, aktif rendah aktif

Notif1 - inverter tristate, aktif tinggi aktif

Example:  
   Module gate() 
   Wire out0; 
   Wire out1; 
   
   Reg in0,in1;
   Not U1(out0,in0); 
   Buf U2(out0,in0);

Jenis Data

Nilai Set

Verilog terdiri dari, terutama, empat nilai dasar. Semua tipe data Verilog, yang digunakan di Verilog menyimpan nilai-nilai ini -

0 (logika nol, atau kondisi salah)

1 (logika satu, atau kondisi benar)

x (nilai logika tidak diketahui)

z (status impedansi tinggi)

penggunaan x dan z sangat terbatas untuk sintesis.

Kawat

Kawat digunakan untuk merepresentasikan kabel fisik dalam suatu rangkaian dan digunakan untuk koneksi gerbang atau modul. Nilai kabel hanya dapat dibaca dan tidak ditetapkan dalam fungsi atau blok. Sebuah kabel tidak dapat menyimpan nilai tetapi selalu didorong oleh pernyataan penugasan berkelanjutan atau dengan menghubungkan kabel ke keluaran dari sebuah gerbang / modul. Jenis kabel khusus lainnya adalah -

Wand (wired-AND) - di sini nilai Wand bergantung pada logika AND dari semua driver perangkat yang terhubung dengannya.

Wor (wired-OR) - di sini nilai Wor bergantung pada OR logis dari semua driver perangkat yang terhubung dengannya.

Tri (three-state) - disini semua driver yang terhubung ke tri harus z, kecuali hanya satu (yang menentukan nilai tri).

Example: 
   Wire [msb:lsb] wire_variable_list; 
   Wirec // simple wire 
   Wand d; 
   
   Assign d = a; // value of d is the logical AND of 
   Assign d = b; // a and b 
   Wire [9:0] A; // a cable (vector) of 10 wires. 
   
   Wand [msb:lsb] wand_variable_list; 
   Wor [msb:lsb] wor_variable_list; 
   Tri [msb:lsb] tri_variable_list;

Daftar

Reg (register) adalah objek data, yang menyimpan nilai dari satu tugas prosedural ke tugas berikutnya dan hanya digunakan dalam fungsi dan blok prosedural yang berbeda. Reg adalah Verilog sederhana, register tipe variabel dan tidak dapat menyiratkan register fisik. Pada register multi bit, data disimpan dalam bentuk unsigned number dan tidak digunakan extension sign.

Contoh -

reg c; // variabel register 1-bit tunggal

reg [5: 0] permata; // vektor 6-bit;

reg [6: 0] d, e; // dua variabel 7-bit

Masukan, Keluaran, Masuk

Kata kunci ini digunakan untuk mendeklarasikan port input, output, dan dua arah dari tugas atau modul. Disini port input dan inout, yang bertipe wire dan port output dikonfigurasikan menjadi wire, reg, wand, wor atau tri type. Selalu, defaultnya adalah tipe kabel.

Example

Module sample(a, c, b, d);  
Input c;   // An input where wire is used. 

Output a, b;  // Two outputs where wire is used. 
Output [2:0] d;  /* A three-bit output. One must declare type in a separate statement. */ 
reg [1:0] a;  // The above ‘a’ port is for declaration in reg.

Bilangan bulat

Bilangan bulat digunakan dalam variabel tujuan umum. Mereka digunakan terutama di loop-indikasi, konstanta, dan parameter. Mereka adalah tipe data tipe 'reg'. Mereka menyimpan data sebagai nomor yang ditandatangani sedangkan jenis reg yang dideklarasikan secara eksplisit menyimpannya sebagai data yang tidak ditandatangani. Jika integer tidak ditentukan pada saat kompilasi, maka ukuran defaultnya adalah 32 bit.

Jika integer memiliki konstanta, penyintesis menyesuaikannya dengan lebar minimum yang diperlukan pada saat kompilasi.

Example

Integer c;   // single 32-bit integer 
Assign a = 63;  // 63 defaults to a 7-bit variable.

Persediaan0, Persediaan1

Supply0 mendefinisikan kabel yang diikat ke logika 0 (ground) dan supply1 mendefinisikan kabel yang diikat ke logika 1 (power).

Example

supply0 logic_0_wires; 
supply0 gnd1;  // equivalent to a wire assigned as 0 

supply1 logic_1_wires; 
supply1 c, s;

Waktu

Waktu adalah besaran 64-bit yang dapat digunakan bersama dengan tugas sistem waktu $ untuk menahan waktu simulasi. Waktu tidak didukung untuk sintesis dan karenanya hanya digunakan untuk tujuan simulasi.

Example

time time_variable_list; 
time c; 
c = $time;   //c = current simulation time

Parameter

Parameter menentukan konstanta yang dapat disetel saat Anda menggunakan modul, yang memungkinkan penyesuaian modul selama proses pembuatan instance.

Example 
Parameter add = 3’b010, sub = 2’b11; 
Parameter n = 3; 
Parameter [2:0] param2 = 3’b110; 

reg [n-1:0] jam; /* A 3-bit register with length of n or above. */ 
always @(z) 
y = {{(add - sub){z}};  

if (z)
begin 
   state = param2[1];
else
   state = param2[2]; 
end

Operator

Operator Aritmatika

Operator ini melakukan operasi aritmatika. Tanda + dan −digunakan sebagai operator uner (x) atau biner (z − y).

Operator yang termasuk dalam operasi aritmatika adalah -

+ (penambahan), - (pengurangan), * (perkalian), / (pembagian),% (modulus)

Example -

parameter v = 5;
reg[3:0] b, d, h, i, count; 
h = b + d; 
i = d - v; 
cnt = (cnt +1)%16; //Can count 0 thru 15.

Operator Relasional

Operator ini membandingkan dua operan dan mengembalikan hasilnya dalam satu bit, 1 atau 0.

Variabel wire dan reg bertanda positif. Jadi (−3'd001) = = 3'd111 dan (−3b001)> 3b110.

Operator yang termasuk dalam operasi relasional adalah -

• == (sama dengan)
• ! = (tidak sama dengan)
• > (lebih dari)
• > = (lebih besar dari atau sama dengan)
• <(kurang dari)
• <= (kurang dari atau sama dengan)

Example

if (z = = y) c = 1; 
   else c = 0; // Compare in 2’s compliment; d>b 
reg [3:0] d,b; 

if (d[3]= = b[3]) d[2:0] > b[2:0]; 
   else b[3]; 
Equivalent Statement 
e = (z == y);

Operator yang Bijaksana

Operator bit-bijaksana yang melakukan perbandingan bit-demi-bit antara dua operan.

Operator yang termasuk dalam operasi Bit bijaksana adalah -

• & (bitwise AND)
• | (bitwiseOR)
• ~ (TIDAK bitwise)
• ^ (XOR bitwise)
• ~ ^ atau ^ ~ (bitwise XNOR)

Example

module and2 (d, b, c); 
input [1:0] d, b; 
output [1:0] c; 
assign c = d & b; 
end module

Operator Logis

Operator logika adalah operator yang bijak dan hanya digunakan untuk operan bit tunggal. Mereka mengembalikan nilai bit tunggal, 0 atau 1. Mereka dapat bekerja pada bilangan bulat atau sekelompok bit, ekspresi dan memperlakukan semua nilai bukan nol sebagai 1. Operator logika umumnya, digunakan dalam pernyataan bersyarat karena mereka bekerja dengan ekspresi.

Operator yang termasuk dalam operasi Logical adalah -

• ! (logika NOT)
• && (logis AND)
• || (logis ATAU)

Example

wire[7:0] a, b, c; // a, b and c are multibit variables. 
reg x; 

if ((a == b) && (c)) x = 1; //x = 1 if a equals b, and c is nonzero. 
   else x = !a; // x =0 if a is anything but zero.

Operator Pengurangan

Operator reduksi adalah bentuk unary dari operator bitwise dan beroperasi pada semua bit vektor operan. Ini juga mengembalikan nilai bit tunggal.

Operator yang termasuk dalam operasi Reduction adalah -

• & (pengurangan AND)
• | (pengurangan ATAU)
• ~ & (pengurangan NAND)
• ~ | (pengurangan NOR)
• ^ (pengurangan XOR)
• ~ ^ atau ^ ~ (pengurangan XNOR)

Example

Module chk_zero (x, z); 

Input [2:0] x; 
Output z; 
Assign z = & x; // Reduction AND 
End module

Operator Shift

Operator shift, yang menggeser operan pertama dengan jumlah bit yang ditentukan oleh operan kedua dalam sintaks. Posisi kosong diisi dengan angka nol untuk kedua arah, shift kiri dan kanan (Tidak ada ekstensi rambu).

Operator yang termasuk dalam operasi Shift adalah -

• << (geser kiri)
• >> (geser ke kanan)

Example

Assign z = c << 3; /* z = c shifted left 3 bits;

Posisi kosong diisi dengan 0 * /

Operator Penggabungan

Operator penggabungan menggabungkan dua atau lebih operan untuk membentuk vektor yang lebih besar.

Operator yang termasuk dalam operasi Concatenation adalah - {} (concatenation)

Example

wire [1:0] a, h; wire [2:0] x; wire [3;0] y, Z; 
assign x = {1’b0, a}; // x[2] = 0, x[1] = a[1], x[0] = a[0] 
assign b = {a, h}; /* b[3] = a[1], b[2] = a[0], b[1] = h[1], 
b[0] = h[0] */ 
assign {cout, b} = x + Z; // Concatenation of a result

Operator Replikasi

Operator replikasi membuat banyak salinan dari sebuah item.

Operator yang digunakan dalam operasi Replikasi adalah - {n {item}} (n replikasi lipat dari sebuah item)

Example

Wire [1:0] a, f; wire [4:0] x; 
Assign x = {2{1’f0}, a}; // Equivalent to x = {0,0,a } 
Assign y = {2{a}, 3{f}}; //Equivalent to y = {a,a,f,f} 
For synthesis, Synopsis did not like a zero replication.

For example:- 
Parameter l = 5, k = 5; 
Assign x = {(l-k){a}}

Operator Bersyarat

Operator bersyarat melakukan sintesis ke multiplexer. Ini adalah jenis yang sama seperti yang digunakan di C / C ++ dan mengevaluasi salah satu dari dua ekspresi berdasarkan kondisinya.

Operator yang digunakan dalam operasi Bersyarat adalah -

(Kondisi) ? (Hasil jika kondisi benar) -

(hasil jika kondisi salah)

Example

Assign x = (g) ? a : b; 
Assign x = (inc = = 2) ? x+1 : x-1; 
/* if (inc), x = x+1, else x = x-1 */

Operand

Literals

Literal adalah operan bernilai konstan yang digunakan dalam ekspresi Verilog. Dua literal Verilog yang umum digunakan adalah -

• String - Operand literal string adalah larik karakter satu dimensi, yang diapit oleh tanda kutip ganda ("").

• Numeric - Operan bilangan konstan ditentukan dalam Bilangan biner, oktal, desimal atau heksadesimal.

Example

n - integer mewakili jumlah bit

F - salah satu dari empat kemungkinan format dasar -

b untuk biner, o untuk oktal, d untuk desimal, h untuk heksadesimal.

“time is”  // string literal 
267        // 32-bit decimal number 
2’b01      // 2-bit binary 
20’hB36F   // 20-bit hexadecimal number 
‘062       // 32-bit octal number

Kabel, Reg, dan Parameter

Kabel, regs, dan parameter adalah tipe data yang digunakan sebagai operan dalam ekspresi Verilog.

Pilihan Bit "x [2]" dan Pemilihan Bagian "x [4: 2]"

Bit-pilih dan pilih-bagian digunakan untuk memilih satu bit dan beberapa bit, masing-masing, dari kawat, reg atau vektor parameter dengan menggunakan tanda kurung siku "[]". Bit-pilih dan pilih-bagian juga digunakan sebagai operan dalam ekspresi dengan cara yang sama seperti objek data utamanya digunakan.

Example

reg [7:0] x, y; 
reg [3:0] z; 
reg a; 
a = x[7] & y[7];      // bit-selects 
z = x[7:4] + y[3:0];  // part-selects

Panggilan Fungsi

Dalam pemanggilan Fungsi, nilai hasil dari suatu fungsi digunakan secara langsung dalam ekspresi tanpa perlu menetapkannya terlebih dahulu ke register atau wire. Ini hanya menempatkan pemanggilan fungsi sebagai salah satu jenis operand. Anda perlu memastikan bahwa Anda mengetahui lebar bit dari nilai kembali pemanggilan fungsi.

Example  
Assign x = y & z & chk_yz(z, y); // chk_yz is a function 

. . ./* Definition of the function */ 
Function chk_yz; // function definition 
Input z,y; 
chk_yz = y^z; 
End function

Modul

Deklarasi Modul

Di Verilog, modul A adalah entitas desain utama. Ini menunjukkan nama dan daftar port (argumen). Beberapa baris berikutnya yang menentukan jenis input / output (input, output atau inout) dan lebar setiap port. Lebar port default hanya 1 bit. Variabel port harus dideklarasikan dengan wire, wand ,. . ., reg. Variabel port default adalah kabel. Biasanya, input adalah kabel karena datanya terkunci di luar modul. Output adalah tipe reg jika sinyalnya disimpan di dalam.

Example

module sub_add(add, in1, in2, out); 
input add; // defaults to wire 
input [7:0] in1, in2; wire in1, in2; 

output [7:0] out; reg out; 
... statements ... 
End module

Penugasan Berkelanjutan

Tugas berkelanjutan dalam Modul digunakan untuk menetapkan nilai ke kabel, yang merupakan tugas normal yang digunakan di luar blok selalu atau awal. Penugasan ini dilakukan dengan pernyataan penetapan eksplisit atau untuk menetapkan nilai ke kawat selama deklarasinya. Penugasan berkelanjutan terus dijalankan pada saat simulasi. Urutan pernyataan assign tidak mempengaruhinya. Jika Anda melakukan perubahan pada salah satu sinyal input sisi kanan, ini akan mengubah sinyal output sisi kiri.

Example

Wire [1:0] x = 2’y01;   // assigned on declaration 
Assign y = c | d;       // using assign statement 
Assign d = a & b; 
/* the order of the assign statements does not matter. */

Modul Instansiasi

Deklarasi modul adalah template untuk membuat objek sebenarnya. Modul dibuat di dalam modul lain, dan setiap instance membuat satu objek dari template itu. Pengecualiannya adalah modul tingkat atas yang merupakan instansinya sendiri. Port modul harus cocok dengan yang ditentukan dalam template. Ini ditentukan -

• By name, menggunakan titik ".template port name (nama kabel yang terhubung ke port)". Atau

• By position, menempatkan port di tempat yang sama di daftar port dari template dan instance.

Example

MODULE DEFINITION 
Module and4 (x, y, z); 
Input [3:0] x, y; 
Output [3:0] z; 
Assign z = x | y; 
End module

Model perilaku di Verilog berisi pernyataan prosedural, yang mengontrol simulasi dan memanipulasi variabel dari tipe data. Semua pernyataan ini terkandung dalam prosedur. Setiap prosedur memiliki aliran aktivitas yang terkait dengannya.

Selama simulasi model perilaku, semua aliran yang ditentukan oleh pernyataan 'selalu' dan 'awal' dimulai bersamaan pada waktu simulasi 'nol'. Pernyataan awal dijalankan satu kali, dan pernyataan selalu dieksekusi secara berulang. Dalam model ini, variabel register a dan b diinisialisasi ke biner 1 dan 0 masing-masing pada waktu simulasi 'nol'. Pernyataan awal kemudian diselesaikan dan tidak dijalankan lagi selama simulasi dijalankan. Pernyataan awal ini berisi blok awal-akhir (juga disebut blok sekuensial) pernyataan. Dalam blok tipe awal-akhir ini, a diinisialisasi terlebih dahulu diikuti oleh b.

Contoh Pemodelan Perilaku

module behave; 
reg [1:0]a,b; 

initial 
begin 
   a = ’b1; 
   b = ’b0; 
end 

always 
begin 
   #50 a = ~a; 
end 

always 
begin 
   #100 b = ~b; 
end 
End module

Penugasan Prosedural

Tugas prosedural adalah untuk memperbarui variabel reg, integer, waktu, dan memori. Ada perbedaan yang signifikan antara penugasan prosedural dan penugasan berkelanjutan seperti yang dijelaskan di bawah ini -

Penugasan berkelanjutan mendorong variabel bersih dan dievaluasi serta diperbarui setiap kali operan input mengubah nilai.

Tugas prosedural memperbarui nilai variabel register di bawah kendali konstruksi aliran prosedural yang mengelilinginya.

Sisi kanan tugas prosedural dapat berupa ekspresi apa pun yang mengevaluasi suatu nilai. Namun, pemilihan bagian di sisi kanan harus memiliki indeks konstan. Sisi kiri menunjukkan variabel yang menerima tugas dari sisi kanan. Sisi kiri penugasan prosedural dapat mengambil salah satu dari bentuk berikut -

• register, integer, real, atau time variable - Penugasan ke referensi nama dari salah satu tipe data ini.

• bit-pilih dari register, integer, real, atau variabel waktu - Sebuah tugas ke satu bit yang meninggalkan bit lainnya tidak tersentuh.

• part-select dari register, integer, real, atau time variable - Part-select dari dua atau lebih bit yang berdekatan yang membiarkan sisa bit tidak tersentuh. Untuk formulir pilih-bagian, hanya ekspresi konstan yang legal.

• elemen memori - Satu kata dari memori. Perhatikan bahwa bit-pilih dan pilih-bagian adalah ilegal pada referensi elemen memori.

• Rangkaian salah satu dari yang di atas - Rangkaian dari salah satu dari empat bentuk sebelumnya dapat ditentukan, yang secara efektif mempartisi hasil ekspresi sisi kanan dan menetapkan bagian partisi, secara berurutan, ke berbagai bagian penggabungan.

Penundaan dalam Tugas (bukan untuk sintesis)

Dalam penugasan tertunda Δt unit waktu berlalu sebelum pernyataan dieksekusi dan penugasan kiri dibuat. Dengan penundaan intra-penugasan, sisi kanan dievaluasi segera tetapi ada penundaan Δt sebelum hasilnya ditempatkan di penugasan kiri. Jika prosedur lain mengubah sinyal sisi kanan selama Δt, itu tidak mempengaruhi output. Penundaan tidak didukung oleh alat sintesis.

Sintaksis

• Procedural Assignmentvariabel = ekspresi

• Delayed assignment# Δt variabel = ekspresi;

• Intra-assignment delayvariabel = ekspresi # Δt;

Contoh

reg [6:0] sum; reg h, ziltch; 
sum[7] = b[7] ^ c[7]; // execute now. 
ziltch = #15 ckz&h; /* ckz&a evaluated now; ziltch changed 
after 15 time units. */ 

#10 hat = b&c; /* 10 units after ziltch changes, b&c is
evaluated and hat changes. */

Memblokir Tugas

Pernyataan tugas prosedural pemblokiran harus dijalankan sebelum eksekusi pernyataan yang mengikutinya dalam blok berurutan. Pernyataan penetapan prosedural pemblokiran tidak mencegah eksekusi pernyataan yang mengikutinya dalam blok paralel.

Sintaksis

Sintaks untuk penetapan prosedural pemblokiran adalah sebagai berikut -

<lvalue> = <timing_control> <expression>

Di mana, lvalue adalah tipe data yang valid untuk pernyataan penugasan prosedural, = adalah operator penugasan, dan kontrol waktu adalah penundaan intra-penugasan opsional. Penundaan kontrol waktu dapat berupa kontrol penundaan (misalnya, # 6) atau kontrol peristiwa (misalnya, @ (posedge clk)). Ekspresi adalah nilai sisi kanan yang ditetapkan simulator ke sisi kiri. The = operator penugasan yang digunakan dengan memblokir penugasan prosedural juga digunakan oleh penugasan berkelanjutan prosedural dan penugasan berkelanjutan.

Contoh

rega = 0; 
rega[3] = 1;            // a bit-select 
rega[3:5] = 7;          // a part-select 
mema[address] = 8’hff;  // assignment to a memory element 
{carry, acc} = rega + regb;  // a concatenation

Tugas Nonblocking (RTL)

Tugas prosedural non-pemblokiran memungkinkan Anda untuk menjadwalkan tugas tanpa memblokir aliran prosedural. Anda dapat menggunakan pernyataan prosedural non-pemblokiran kapan pun Anda ingin membuat beberapa tugas register dalam langkah waktu yang sama tanpa memperhatikan urutan atau ketergantungan satu sama lain.

Sintaksis

Sintaks untuk penetapan prosedural non-pemblokiran adalah sebagai berikut -

<lvalue> <= <timing_control> <expression>

Di mana lvalue adalah tipe data yang valid untuk pernyataan penugasan prosedural, <= adalah operator penugasan non-pemblokiran, dan kontrol waktu adalah pengontrol waktu intra-penetapan opsional. Penundaan kontrol waktu dapat berupa kontrol penundaan atau kontrol peristiwa (misalnya, @ (posedge clk)). Ekspresi adalah nilai sisi kanan yang ditetapkan simulator ke sisi kiri. Operator penetapan non-pemblokiran adalah operator yang sama dengan yang digunakan simulator untuk operator relasional yang kurang dari orequal. Simulator menafsirkan operator <= menjadi operator relasional saat Anda menggunakannya dalam ekspresi, dan menafsirkan operator <= sebagai operator penugasan saat Anda menggunakannya dalam konstruksi penetapan prosedural non-pemblokiran.

Bagaimana simulator mengevaluasi tugas prosedural non-pemblokiran Ketika simulator menemukan tugas prosedural non-pemblokiran, simulator mengevaluasi dan menjalankan penetapan prosedural non-pemblokiran dalam dua langkah sebagai berikut -

• Simulator mengevaluasi sisi kanan dan menjadwalkan penugasan nilai baru untuk dilakukan pada waktu yang ditentukan oleh kontrol waktu prosedural. Simulator mengevaluasi sisi kanan dan menjadwalkan penugasan nilai baru untuk dilakukan pada waktu yang ditentukan oleh kontrol waktu prosedural.

• Di akhir langkah waktu, di mana penundaan yang diberikan telah kedaluwarsa atau peristiwa yang sesuai telah terjadi, simulator menjalankan tugas dengan menetapkan nilai ke sisi kiri.

Contoh

module evaluates2(out); 
output out; 
reg a, b, c; 
initial 

begin 
   a = 0; 
   b = 1; 
   c = 0; 
end 
always c = #5 ~c; 
always @(posedge c) 

begin 
   a <= b; 
   b <= a; 
end 
endmodule

Kondisi

Pernyataan bersyarat (atau pernyataan if-else) digunakan untuk membuat keputusan, apakah pernyataan dieksekusi atau tidak.

Secara formal, sintaksnya adalah sebagai berikut -

<statement> 
::= if ( <expression> ) <statement_or_null> 
||= if ( <expression> ) <statement_or_null> 
   else <statement_or_null> 
<statement_or_null> 

::= <statement> 
||= ;

<ekspresi> dievaluasi; jika benar (yaitu, memiliki nilai yang bukan nol yang diketahui), pernyataan pertama dijalankan. Jika salah (memiliki nilai nol atau nilainya x atau z), pernyataan pertama tidak dijalankan. Jika ada pernyataan lain dan <ekspresi> salah, pernyataan lain dijalankan. Karena, nilai numerik dari ekspresi if diuji menjadi nol, pintasan tertentu dimungkinkan.

Misalnya, dua pernyataan berikut mengungkapkan logika yang sama -

if (expression) 
if (expression != 0)

Karena, bagian lain dari if-else bersifat opsional, dapat terjadi kebingungan saat else dihilangkan dari urutan if bersarang. Ini diselesaikan dengan selalu mengaitkan else dengan yang terdekat sebelumnya jika itu kekurangan yang lain.

Contoh

if (index > 0) 
if (rega > regb) 
   result = rega; 
   else // else applies to preceding if 
   result = regb; 

If that association is not what you want, use a begin-end block statement 
to force the proper association 

if (index > 0) 
begin 

if (rega > regb) 
result = rega; 
end 
   else 
   result = regb;

Konstruksi dari: if- else- if

Konstruksi berikut terjadi begitu sering sehingga perlu pembahasan terpisah singkat.

Example

if (<expression>) 
   <statement> 
   else if (<expression>) 
   <statement> 
   else if (<expression>) 
   <statement> 
   else  
   <statement>

Urutan if ini (dikenal sebagai konstruk if-else-if) adalah cara paling umum untuk menulis keputusan multi-arah. Ekspresi dievaluasi secara berurutan; jika ada ekspresi yang benar, pernyataan yang terkait dengannya dijalankan, dan ini mengakhiri seluruh rantai. Setiap pernyataan adalah satu pernyataan atau satu blok pernyataan.

Bagian lain yang terakhir dari konstruksi if-else-if menangani kasus 'none of the above' atau default di mana tidak ada kondisi lain yang terpenuhi. Terkadang tidak ada tindakan eksplisit untuk default; dalam hal ini, trailing else dapat dihilangkan atau dapat digunakan untuk pengecekan error untuk menangkap kondisi yang tidak mungkin.

Pernyataan Kasus

Pernyataan kasus adalah pernyataan keputusan multi-arah khusus yang menguji apakah ekspresi cocok dengan salah satu dari sejumlah ekspresi lain, dan bercabang sesuai. Pernyataan kasus berguna untuk menjelaskan, misalnya, decoding dari instruksi mikroprosesor. Pernyataan kasus memiliki sintaks berikut -

Example

<statement> 
::= case ( <expression> ) <case_item>+ endcase 
||= casez ( <expression> ) <case_item>+ endcase 
||= casex ( <expression> ) <case_item>+ endcase 
<case_item> 
::= <expression> <,<expression>>* : <statement_or_null> 
||= default : <statement_or_null> 
||= default <statement_or_null>

Ekspresi kasus dievaluasi dan dibandingkan dalam urutan yang tepat yang diberikan. Selama pencarian linier, jika salah satu ekspresi item kasus cocok dengan ekspresi dalam tanda kurung, maka pernyataan yang terkait dengan item kasus tersebut dijalankan. Jika semua perbandingan gagal, dan item default diberikan, maka pernyataan item default dijalankan. Jika pernyataan default tidak diberikan, dan semua perbandingan gagal, maka tidak ada pernyataan item kasus yang dijalankan.

Terlepas dari sintaks, pernyataan case berbeda dari konstruksi multi-cara if-else-if dalam dua cara penting -

• Ekspresi kondisional dalam konstruk if-else-if lebih umum daripada membandingkan satu ekspresi dengan beberapa ekspresi lainnya, seperti dalam pernyataan case.

• Pernyataan case memberikan hasil yang pasti ketika ada nilai x dan z dalam ekspresi.

Pernyataan Perulangan

Ada empat jenis pernyataan perulangan. Mereka menyediakan sarana untuk mengontrol eksekusi pernyataan nol, satu kali, atau lebih.

• selamanya terus menjalankan pernyataan.

• repeat mengeksekusi pernyataan beberapa kali.

• sementara mengeksekusi pernyataan sampai ekspresi menjadi salah. Jika ekspresi diawali salah, pernyataan tersebut tidak dieksekusi sama sekali.

• untuk kontrol eksekusi pernyataan terkait dengan proses tiga langkah, sebagai berikut -

  • Menjalankan tugas yang biasanya digunakan untuk menginisialisasi variabel yang mengontrol jumlah loop yang dijalankan

  • Mengevaluasi ekspresi — jika hasilnya nol, loop for keluar, dan jika bukan nol, loop for mengeksekusi pernyataan terkait dan kemudian melakukan langkah 3

  • Jalankan tugas yang biasanya digunakan untuk mengubah nilai variabel loopcontrol, lalu ulangi langkah 2

Berikut ini adalah aturan sintaks untuk pernyataan perulangan -

Example

<statement> 
::= forever <statement> 
||=forever 
begin 
   <statement>+ 
end  

<Statement> 
::= repeat ( <expression> ) <statement> 
||=repeat ( <expression> ) 
begin
   <statement>+ 
end  

<statement> 
::= while ( <expression> ) <statement> 
||=while ( <expression> ) 
begin 
   <statement>+ 
end  
<statement> 
::= for ( <assignment> ; <expression> ; <assignment> ) 
<statement> 
||=for ( <assignment> ; <expression> ; <assignment> ) 
begin 
   <statement>+ 
end

Kontrol Penundaan

Kontrol Penundaan

Eksekusi pernyataan prosedural dapat dikendalikan dengan penundaan dengan menggunakan sintaks berikut -

<statement> 
::= <delay_control> <statement_or_null> 
<delay_control> 
::= # <NUMBER> 
||= # <identifier> 
||= # ( <mintypmax_expression> )

Contoh berikut menunda pelaksanaan tugas sebanyak 10 unit waktu -

# 10 rega = regb;

Tiga contoh berikutnya memberikan ekspresi mengikuti tanda angka (#). Pelaksanaan penundaan tugas dengan jumlah waktu simulasi yang ditentukan oleh nilai ekspresi.

Kontrol Acara

Pelaksanaan pernyataan prosedural dapat disinkronkan dengan perubahan nilai pada net atau register, atau terjadinya peristiwa yang dideklarasikan, dengan menggunakan sintaks kontrol peristiwa berikut -

Example

<statement> 
::= <event_control> <statement_or_null> 

<event_control> 
::= @ <identifier> 
||= @ ( <event_expression> ) 

<event_expression> 
::= <expression> 
||= posedge <SCALAR_EVENT_EXPRESSION> 
||= negedge <SCALAR_EVENT_EXPRESSION> 
||= <event_expression> <or <event_expression>>

* <SCALAR_EVENT_EXPRESSION> adalah ekspresi yang memutuskan nilai satu bit.

Perubahan nilai pada net dan register dapat digunakan sebagai event untuk memicu eksekusi sebuah pernyataan. Ini dikenal sebagai mendeteksi kejadian implisit. Sintaks Verilog juga memungkinkan Anda mendeteksi perubahan berdasarkan arah perubahan — yaitu, menuju nilai 1 (posedge) atau menuju nilai 0 (negedge). Perilaku posedge dan negedge untuk nilai ekspresi yang tidak diketahui adalah sebagai berikut -

• sebuah negedge terdeteksi pada transisi dari 1 ke tidak diketahui dan dari tidak diketahui ke 0
• sebuah posedge terdeteksi pada transisi dari 0 ke tidak diketahui dan dari tidak diketahui ke 1

Prosedur: Selalu dan Pemblokiran Awal

Semua prosedur di Verilog ditentukan dalam salah satu dari empat Blok berikut. 1) Blok awal 2) Selalu blok 3) Tugas 4) Fungsi

Pernyataan awal dan selalu diaktifkan pada awal simulasi. Blok awal hanya dijalankan satu kali dan aktivitasnya mati saat pernyataan selesai. Sebaliknya, blok selalu dieksekusi berulang kali. Aktivitasnya hanya mati jika simulasi dihentikan. Tidak ada batasan jumlah blok awal dan selalu yang dapat ditentukan dalam modul. Tugas dan fungsi adalah prosedur yang diaktifkan dari satu atau lebih tempat di prosedur lain.

Blok Awal

Sintaks untuk pernyataan awal adalah sebagai berikut -

<initial_statement> 
::= initial <statement>

Contoh berikut mengilustrasikan penggunaan pernyataan awal untuk inisialisasi variabel pada awal simulasi.

Initial 
Begin 
   Areg = 0; // initialize a register 
   For (index = 0; index < size; index = index + 1) 
   Memory [index] = 0; //initialize a memory 
   Word 
End

Penggunaan khas lain dari Blok awal adalah spesifikasi deskripsi bentuk gelombang yang dijalankan sekali untuk memberikan stimulus ke bagian utama rangkaian yang disimulasikan.

Initial 
Begin 
   Inputs = ’b000000; 
   // initialize at time zero 
   #10 inputs = ’b011001; // first pattern 
   #10 inputs = ’b011011; // second pattern 
   #10 inputs = ’b011000; // third pattern 
   #10 inputs = ’b001000; // last pattern 
End

Selalu Memblokir

Pernyataan 'selalu' berulang terus menerus selama simulasi dijalankan. Sintaks untuk pernyataan selalu diberikan di bawah ini

<always_statement> 
::= always <statement>

Pernyataan 'selalu', karena sifat perulangannya, hanya berguna bila digunakan bersama dengan beberapa bentuk kontrol waktu. Jika pernyataan 'selalu' tidak memberikan waktu untuk maju, pernyataan 'selalu' menciptakan kondisi kebuntuan simulasi. Kode berikut, misalnya, membuat loop zero-delay tak terbatas -

Always areg = ~areg;

Memberikan kontrol waktu ke kode di atas membuat deskripsi yang berpotensi berguna — seperti pada contoh berikut -

Always #half_period areg = ~areg;