Contabilità dei costi - Analisi CVP

L'analisi costo-volume-profitto (CVP) è anche nota come analisi di pareggio. Ogni organizzazione aziendale lavora per massimizzare i propri profitti. Con l'aiuto dell'analisi CVP, la direzione studia la correlazione tra profitto e livello di produzione.

L'analisi CVP si occupa del livello di attività in cui le vendite totali sono uguali al costo totale e viene chiamato punto di pareggio. In altre parole, studiamo il valore delle vendite, il costo e il profitto a diversi livelli di produzione. L'analisi del CVP evidenzia la relazione tra il costo, il valore delle vendite e il profitto.

Presupposti

Esaminiamo le ipotesi per l'analisi CVP:

I costi variabili rimangono variabili e i costi fissi rimangono statici ad ogni livello di produzione.
Il volume delle vendite non influisce sul prezzo di vendita del prodotto. Possiamo assumere come costante il prezzo di vendita.
A tutti i livelli di vendita, il volume, il materiale e il costo del lavoro rimangono costanti.
Efficienza e produttività rimangono invariate a tutti i livelli di volume delle vendite.
Il mix di vendita a tutti i livelli di vendita rimane costante in una situazione multi-prodotto.
Il fattore rilevante che influenza i costi e le entrate è solo il volume.
Il volume delle vendite è uguale al volume della produzione.

Equazione del costo marginale

Le equazioni per gli elementi di costo sono le seguenti:

Sales = Variable costs + Fixed Expenses ± Profit /Loss

                     Or
                     
Sales – Variable Cost = Fixed Expenses ± Profit /Loss

                     Or
                     
Sales – Variable Cost = Contribution

È necessario comprendere i seguenti quattro concetti, i loro calcoli e le applicazioni per conoscere la relazione matematica tra costo, volume e profitto:

Contribution
Rapporto volume profitto (rapporto P / V o contributo / vendite (C / S))
Punto di pareggio
Margine di sicurezza

Contributo

Contribution = Sales – Marginal Cost

Abbiamo già discusso il contributo nell'argomento Costo marginale sopra.

Rapporto profitto-volume

Il rapporto profitto / volume (P / V) viene calcolato studiando la redditività delle operazioni di un'azienda e per stabilire una relazione tra vendite e contributo. È uno dei rapporti più importanti, calcolato come sotto:

Rapporto ^P / _V =

Contributo / vendite

Spese fisse + profitto / vendite

Vendite − Costo / vendite variabile

Variazione dei profitti dei contributi / Variazione delle vendite

Il rapporto P / V condivide un rapporto diretto con i profitti. Più alto è il rapporto P / V, più il profitto e viceversa.

Punto di pareggio

Quando il costo totale di esecuzione dell'attività è uguale al totale delle vendite, si parla di punto di pareggio. Il contributo equivale al costo fisso a questo punto. Ecco una formula per calcolare il punto di pareggio:

BEP (in unità) =

Spese fisse totali / Prezzo di vendita per unità - Costo marginale per unità

Spese fisse totali / contributo per unità

Punto di pareggio in base alle vendite totali:

Rapporto costo fisso / ^P / _V

Calcolo della produzione o del valore delle vendite a cui si ottiene un profitto desiderato:

Spese fisse + profitto / prezzo di vendita desiderati per unità - Costo marginale per unità

Spese fisse + profitto / contributo desiderato per unità

Punto di pareggio composito

Un'azienda può avere diverse unità di produzione, dove possono produrre lo stesso prodotto. In questo caso, il costo fisso combinato di ciascuna unità di produzione e le vendite totali combinate vengono presi in considerazione per scoprire il BEP.

Constant Product - Approccio Mix In questo approccio, il rapporto è costante per i prodotti di tutte le unità produttive.
Variable Product - Approccio misto In questo approccio, la preferenza dei prodotti si basa su un rapporto maggiore.

Margine di sicurezza

L'eccesso di vendita su BEP è noto come margine di sicurezza. Perciò,

Margin of safety = Actual Sales − Sales at BEP

Il margine di sicurezza può essere calcolato con l'aiuto della seguente formula:

Margine di sicurezza =

Rapporto profitto / ^P / _V

Utile / contributo per unità

Grafico di pareggio

Il grafico di pareggio è la rappresentazione grafica più utile del costo marginale. Converte i dati contabili in un utile report leggibile. Profitti, perdite e costi stimati possono essere determinati a diversi livelli di produzione. Facciamo un esempio.

Esempio

Calcola il punto di pareggio e disegna il grafico di pareggio dai seguenti dati:

Fixed Cost    = Rs 2,50,000
Variable Cost = Rs 15 per unit
Selling Price = Rs 25 per unit
Production level in units 12,000, 15,000, 20,000, 25,000, 30,000, and 40,000.

Solution:

BEP =

Costo fisso / contributo per unità

Rs 2,50.000 / Rs 10 × (Rs 25 - Rs 15)

= 25.000 unità

A livello di produzione di 25.000 unità, il costo totale sarà di Rs 6,25.000.

(Calcolato come (25000 × 14) + 2,50000)

Dichiarazione che mostra profitto e margine di sicurezza a diversi livelli di produzione Break Even Sale = Rs 6,25.000 (25.000 x 25)
Produzione (In unità)	Vendita totale (In Rs)	Costo totale (In Rs)	Profitto (Vendite - Costo) (In Rs)	Margine di sicurezza (Utile / Contributo per unità) (In unità)
12000	3.00.000	4,30.000	-1,30.000
15000	3,75.000	4,75.000	-1.00.000
20000	5,00.000	5,50.000	-50.000
25000	6,25.000	6,25.000	(BEP)	(BEP)
30000	7,50.000	7.00.000	50.000	5.000
40000	10.00.000	8,50.000	1.50.000	15.000

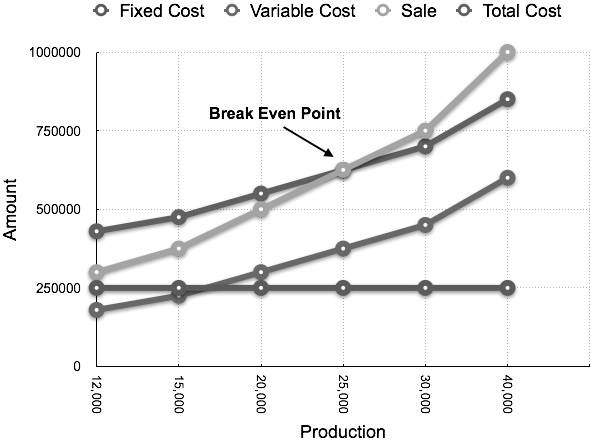
Il grafico corrispondente tracciato come produzione rispetto all'importo appare come segue: