DAA - Percorsi più brevi

Algoritmo di Dijkstra

L'algoritmo di Dijkstra risolve il problema dei cammini minimi da una sola sorgente su un grafo ponderato diretto G = (V, E) , dove tutti gli archi sono non negativi (cioè, w (u, v) ≥ 0 per ogni arco (u, v ) Є E ).

Nel seguente algoritmo, useremo una funzione Extract-Min(), che estrae il nodo con la chiave più piccola.

Algorithm: Dijkstra’s-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
S := Ф 
Q := G.V 
while Q ≠ Ф 
   u := Extract-Min (Q) 
   S := S U {u} 
   for each vertex v Є G.adj[u] 
      if v.d > u.d + w(u, v) 
         v.d := u.d + w(u, v) 
         v.∏ := u

Analisi

La complessità di questo algoritmo dipende completamente dall'implementazione della funzione Extract-Min. Se la funzione di estrazione min è implementata utilizzando la ricerca lineare, la complessità di questo algoritmo èO(V² + E).

In questo algoritmo, se usiamo min-heap su cui Extract-Min() funziona per restituire il nodo da Q con la chiave più piccola, la complessità di questo algoritmo può essere ulteriormente ridotta.

Esempio

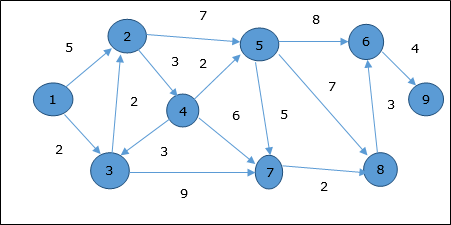
Consideriamo il vertice 1 e 9rispettivamente come vertice iniziale e vertice di destinazione. Inizialmente, tutti i vertici tranne il vertice iniziale sono contrassegnati da ∞ e il vertice iniziale è contrassegnato da0.

Vertice	Iniziale	Passaggio 1 V 1	Passaggio 2 V 3	Passaggio 3 V 2	Passaggio 4 V 4	Passaggio 5 V 5	Passaggio 6 V 7	Passaggio 7 V 8	Passaggio 8 V 6
1	0	0	0	0	0	0	0	0	0
2	∞	5	4	4	4	4	4	4	4
3	∞	2	2	2	2	2	2	2	2
4	∞	∞	∞	7	7	7	7	7	7
5	∞	∞	∞	11	9	9	9	9	9
6	∞	∞	∞	∞	∞	17	17	16	16
7	∞	∞	11	11	11	11	11	11	11
8	∞	∞	∞	∞	∞	16	13	13	13
9	∞	∞	∞	∞	∞	∞	∞	∞	20

Quindi, la distanza minima del vertice 9 dal vertice 1 è 20. E il percorso è

1 → 3 → 7 → 8 → 6 → 9

Questo percorso è determinato in base alle informazioni sul predecessore.

Algoritmo di Bellman Ford

Questo algoritmo risolve il problema del percorso minimo della singola sorgente di un grafo orientato G = (V, E)in cui i pesi dei bordi possono essere negativi. Inoltre, questo algoritmo può essere applicato per trovare il percorso più breve, se non esiste alcun ciclo ponderato negativo.

Algorithm: Bellman-Ford-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
for i = 1 to |G.V| - 1 
   for each edge (u, v) Є G.E 
      if v.d > u.d + w(u, v) 
         v.d := u.d +w(u, v) 
         v.∏ := u 
for each edge (u, v) Є G.E 
   if v.d > u.d + w(u, v) 
      return FALSE 
return TRUE

Analisi

Il primo for loop viene utilizzato per l'inizializzazione, che viene eseguita in O(V)volte. Il prossimofor il ciclo viene eseguito |V - 1| passa oltre i bordi, che prendeO(E) volte.

Quindi, l'algoritmo Bellman-Ford viene eseguito O(V, E) tempo.

Esempio

L'esempio seguente mostra passo dopo passo come funziona l'algoritmo Bellman-Ford. Questo grafico ha un margine negativo ma non ha alcun ciclo negativo, quindi il problema può essere risolto utilizzando questa tecnica.

Al momento dell'inizializzazione, tutti i vertici tranne la sorgente sono contrassegnati da ∞ e la sorgente è contrassegnata da 0.

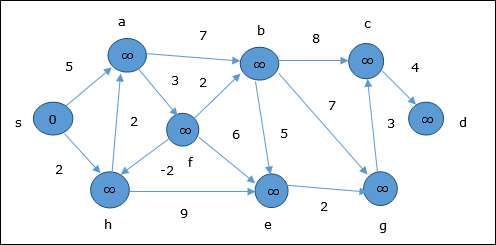
Nella prima fase, tutti i vertici raggiungibili dalla sorgente vengono aggiornati con un costo minimo. Quindi, verticia e h vengono aggiornati.

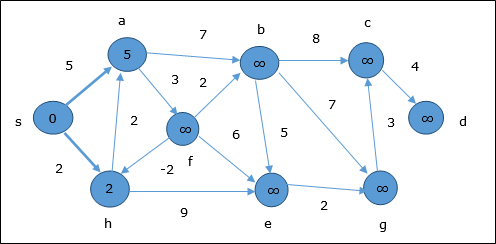
Nella fase successiva, vertici a, b, f e e vengono aggiornati.

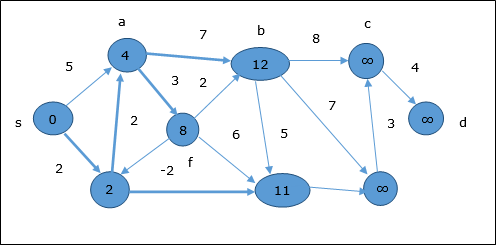
Seguendo la stessa logica, in questo passaggio vertici b, f, c e g vengono aggiornati.

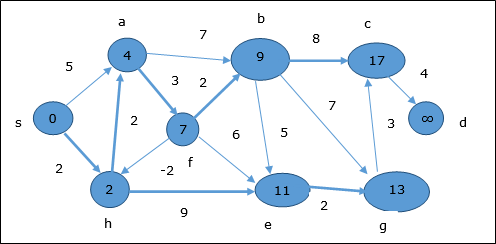
Qui, vertici c e d vengono aggiornati.

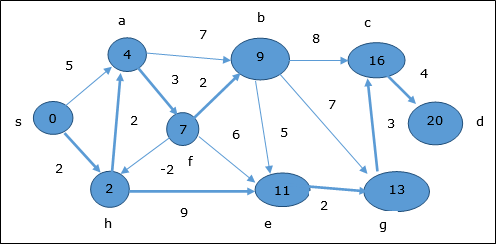
Quindi, la distanza minima tra i vertici s e vertice d è 20.

In base alle informazioni sul predecessore, il percorso è s → h → e → g → c → d