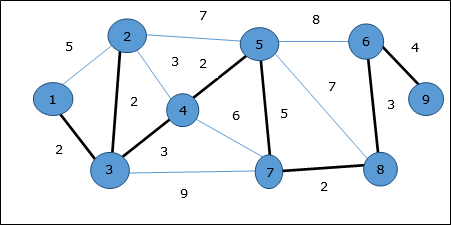
DAA - Spanning Tree

UN spanning tree è un sottoinsieme di un Graph non orientato che ha tutti i vertici collegati da un numero minimo di bordi.

Se tutti i vertici sono collegati in un grafo, esiste almeno uno spanning tree. In un grafico, possono esistere più di uno spanning tree.

Proprietà

• Uno spanning tree non ha alcun ciclo.
• Qualsiasi vertice può essere raggiunto da qualsiasi altro vertice.

Esempio

Nel grafico seguente, i bordi evidenziati formano uno spanning tree.

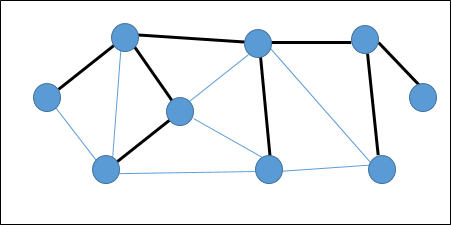
Spanning Tree minimo

UN Minimum Spanning Tree (MST)è un sottoinsieme di bordi di un grafo non orientato ponderato connesso che collega tutti i vertici insieme con il peso del bordo totale minimo possibile. Per derivare un MST, è possibile utilizzare l'algoritmo di Prim o l'algoritmo di Kruskal. Quindi, discuteremo l'algoritmo di Prim in questo capitolo.

Come abbiamo discusso, un grafo può avere più di uno spanning tree. Se ci sonon numero di vertici, lo spanning tree dovrebbe avere n - 1numero di bordi. In questo contesto, se ogni bordo del grafico è associato a un peso ed esistono più di uno spanning tree, dobbiamo trovare lo spanning tree minimo del grafico.

Inoltre, se esistono bordi ponderati duplicati, il grafico può avere più spanning tree minimi.

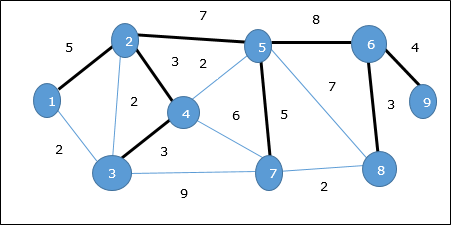
Nel grafico sopra, abbiamo mostrato uno spanning tree sebbene non sia lo spanning tree minimo. Il costo di questo albero di copertura è (5 + 7 + 3 + 3 + 5 + 8 + 3 + 4) = 38.

Useremo l'algoritmo di Prim per trovare lo spanning tree minimo.

Algoritmo di Prim

L'algoritmo di Prim è un approccio avido per trovare l'albero di copertura minimo. In questo algoritmo, per formare un MST possiamo partire da un vertice arbitrario.

Algorithm: MST-Prim’s (G, w, r) 
for each u є G.V 
   u.key = ∞ 
   u.∏ = NIL 
r.key = 0 
Q = G.V 
while Q ≠ Ф 
   u = Extract-Min (Q) 
   for each v є G.adj[u] 
      if each v є Q and w(u, v) < v.key 
         v.∏ = u 
         v.key = w(u, v)

La funzione Extract-Min restituisce il vertice con il minimo costo del bordo. Questa funzione funziona su min-heap.

Esempio

Usando l'algoritmo di Prim, possiamo partire da qualsiasi vertice, partiamo dal vertice 1.

Vertice 3 è connesso al vertice 1 con il minimo costo del bordo, quindi bordo (1, 2) viene aggiunto allo spanning tree.

Avanti, bordo (2, 3) è considerato come questo è il minimo tra i bordi {(1, 2), (2, 3), (3, 4), (3, 7)}.

Nel passaggio successivo, otteniamo vantaggio (3, 4) e (2, 4)con un costo minimo. Bordo(3, 4) è selezionato a caso.

In modo simile, i bordi (4, 5), (5, 7), (7, 8), (6, 8) e (6, 9)sono selezionati. Man mano che tutti i vertici vengono visitati, l'algoritmo si ferma.

Il costo dello spanning tree è (2 + 2 + 3 + 2 + 5 + 2 + 3 + 4) = 23. Non c'è più spanning tree in questo grafico con un costo inferiore a 23.