単位分数のエッジの長さを持つ立方体で作られたソリッドの体積

前書き

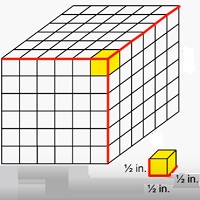
ここでは、単位分数の辺の長さを持つ立方体でできた立体の体積を見つけます。たとえば、エッジの長さが$ \ frac {1} {2} $インチの小さな立方体でできた3インチ×3インチ×3の寸法のソリッドを考えてみます。

その場合、ソリッドは$ \ frac {1} {2} $インチのエッジ長の6×6×6の小さな立方体で構成されます。したがって、この場合の固体の体積は次のようになります。

ボリューム= lwh = $ 6 \ times \ frac {1} {2} \ times 6 \ times \ frac {1} {2} \ times 6 \ times \ frac {1} {2} $

= 3×3×3 = 27立方インチ

単位分数の辺の長さを持つ立方体で作られた固体の体積の式

ソリッドがエッジの立方体であると仮定すると、単位

b =各エッジに沿った単位の端の長さを持つ立方体の数

k =単位分数エッジ長

Volume of solid = b × k × b × k × b × k cubic units

例1

単位分数の辺の長さを持つ立方体の次のソリッドの体積を見つけます。各プリズムの単位はcmで測定されます（縮尺どおりではありません）

Step 1:

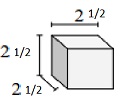
単位分数の辺の長さが$ \ frac {1} {2} $ cmの立方体のソリッド

Step 2:

ボリュームV = lwh = $ 2 \ frac {1} {2} \ times 2 \ frac {1} {2} \ times 2 \ frac {1} {2} $

= $ 5 \ times \ frac {1} {2} \ times 5 \ times \ frac {1} {2} \ times 5 \ times \ frac {1} {2} $

= $ 15 \ frac {5} {8} $ cu cm

例2

単位分数の辺の長さを持つ立方体の次のソリッドの体積を見つけます。各プリズムの単位はcmで測定されます（縮尺どおりではありません）

Step 1:

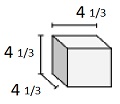
単位分数の辺の長さが$ \ frac {1} {3} $ cmの立方体のソリッド

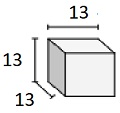
Step 2:

ボリュームV = lwh = $ 4 \ frac {1} {3} \ times 4 \ frac {1} {3} \ times 4 \ frac {1} {3} $

= $ 13 \ times \ frac {1} {3} \ times 13 \ times \ frac {1} {3} \ times 13 \ times \ frac {1} {3} $

= $ 81 \ frac {10} {27} $ cu cm