ファジィ論理-集合論

ファジー集合は、古典的な集合の拡張および大幅な過度の単純化と見なすことができます。これは、セットメンバーシップのコンテキストで最もよく理解できます。基本的に、部分的なメンバーシップが許可されます。つまり、セット内でさまざまな程度のメンバーシップを持つ要素が含まれます。このことから、古典集合とファジィ集合の違いを理解することができます。クラシックセットにはメンバーシップの正確なプロパティを満たす要素が含まれ、ファジーセットにはメンバーシップの不正確なプロパティを満たす要素が含まれます。

数学的概念

情報の世界$ U $のファジー集合$ \ widetilde {A} $は、順序対の集合として定義でき、数学的に次のように表すことができます。

$$ \ widetilde {A} = \ left \ {\ left（y、\ mu _ {\ widetilde {A}} \ left（y \ right）\ right）| y \ in U \ right \} $$

ここで、$ \ mu _ {\ widetilde {A}} \ left（y \ right）$ = \ widetilde {A}の$ y $のメンバーシップの程度は、0から1の範囲の値、つまり$ \ muを想定しています。 _ {\ widetilde {A}}（y）\ in \ left [0,1 \ right] $。

ファジー集合の表現

ここで、情報の世界の2つのケースを検討し、ファジー集合をどのように表現できるかを理解しましょう。

ケース1

情報の宇宙$ U $が離散的で有限である場合−

$$ \ widetilde {A} = \ left \ {\ frac {\ mu _ {\ widetilde {A}} \ left（y_1 \ right）} {y_1} + \ frac {\ mu _ {\ widetilde {A}} \ left（y_2 \ right）} {y_2} + \ frac {\ mu _ {\ widetilde {A}} \ left（y_3 \ right）} {y_3} + ... \ right \} $$

$ = \ left \ {\ sum_ {i = 1} ^ {n} \ frac {\ mu _ {\ widetilde {A}} \ left（y_i \ right）} {y_i} \ right \} $

ケース2

情報の宇宙$ U $が連続的で無限である場合−

$$ \ widetilde {A} = \ left \ {\ int \ frac {\ mu _ {\ widetilde {A}} \ left（y \ right）} {y} \ right \} $$

上記の表現では、合計記号は各要素のコレクションを表しています。

ファジィ集合の操作

2つのファジーセット$ \ widetilde {A} $と$ \ widetilde {B} $、情報のユニバース$ U $とユニバースの要素がある場合、次の関係は、ファジーセットの和集合、共通部分、および補集合の演算を表します。

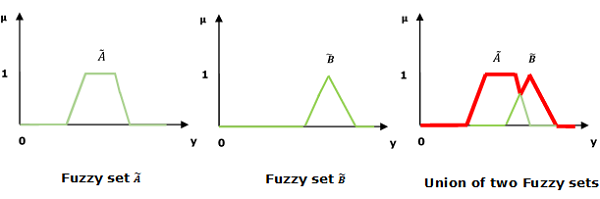
ユニオン/ファジー 'OR'

次の表現を検討して、 Union/Fuzzy ‘OR’ 関係は機能します-

$$ \ mu _ {{\ widetilde {A} \ cup \ widetilde {B}}} \ left（y \ right）= \ mu _ {\ widetilde {A}} \ vee \ mu _ \ widetilde {B} \クワッド\ forall y \ in U $$

ここで、∨は「最大」操作を表します。

交差点/ファジー 'AND'

次の表現を検討して、 Intersection/Fuzzy ‘AND’ 関係は機能します-

$$ \ mu _ {{\ widetilde {A} \ cap \ widetilde {B}}} \ left（y \ right）= \ mu _ {\ widetilde {A}} \ wedge \ mu _ \ widetilde {B} \クワッド\ forall y \ in U $$

ここで、∧は「min」操作を表します。

補完/ファジー 'NOT'

次の表現を検討して、 Complement/Fuzzy ‘NOT’ 関係は機能します-

$$ \ mu _ {\ widetilde {A}} = 1- \ mu _ {\ widetilde {A}} \ left（y \ right）\ quad y \ in U $$

ファジィ集合の性質

ファジー集合のさまざまな特性について説明しましょう。

可換性

2つのファジーセット$ \ widetilde {A} $と$ \ widetilde {B} $がある場合、このプロパティは次のように述べます。

$$ \ widetilde {A} \ cup \ widetilde {B} = \ widetilde {B} \ cup \ widetilde {A} $$

$$ \ widetilde {A} \ cap \ widetilde {B} = \ widetilde {B} \ cap \ widetilde {A} $$

結合プロパティ

3つのファジーセット$ \ widetilde {A} $、$ \ widetilde {B} $、および$ \ widetilde {C} $がある場合、このプロパティは次のように述べます。

$$（\ widetilde {A} \ cup \ left \ widetilde {B}）\ cup \ widetilde {C} \ right = \ left \ widetilde {A} \ cup（\ widetilde {B} \ right）\ cup \ widetilde {C}）$$

$$（\ widetilde {A} \ cap \ left \ widetilde {B}）\ cap \ widetilde {C} \ right = \ left \ widetilde {A} \ cup（\ widetilde {B} \ right \ cap \ widetilde { C}）$$

分配法則

3つのファジーセット$ \ widetilde {A} $、$ \ widetilde {B} $、および$ \ widetilde {C} $がある場合、このプロパティは次のように述べます。

$$ \ widetilde {A} \ cup \ left（\ widetilde {B} \ cap \ widetilde {C} \ right）= \ left（\ widetilde {A} \ cup \ widetilde {B} \ right）\ cap \ left （\ widetilde {A} \ cup \ widetilde {C} \ right）$$

$$ \ widetilde {A} \ cap \ left（\ widetilde {B} \ cup \ widetilde {C} \ right）= \ left（\ widetilde {A} \ cap \ widetilde {B} \ right）\ cup \ left （\ widetilde {A} \ cap \ widetilde {C} \ right）$$