マイクロ波工学-EHプレーンティー

EHプレーンティージャンクションは、2つの単純な導波管を1つは平行で、もう1つは直列で、すでに2つのポートがある長方形の導波管に接続することによって形成されます。これは、Magic Tee、または Hybrid または 3dB coupler。

長方形の導波管のアームは、 collinear ports つまり、ポート1とポート2であり、ポート3は次のように呼ばれます。 H-Arm または Sum port または Parallel port。ポート4は次のように呼ばれますE-Arm または Difference port または Series port。

マジックティーの断面の詳細は、次の図で理解できます。

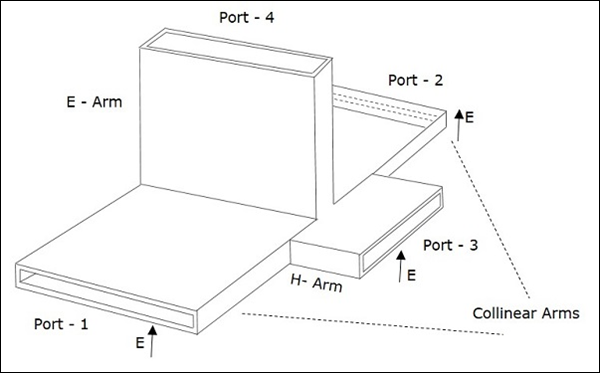
次の図は、パラレルポートとシリアルポートの両方を形成するためにサイドアームによって双方向導波管に接続されていることを示しています。

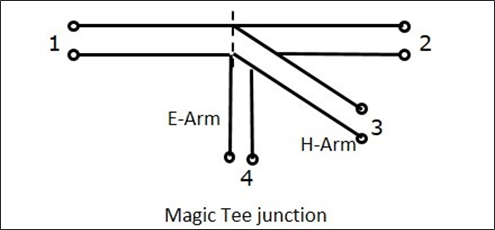
EHプレーンティーの特徴

位相と大きさが等しい信号がポート1とポート2に送信される場合、ポート4の出力はゼロになり、ポート3の出力はポート1と2の両方の加算になります。
信号がポート4（Eアーム）に送信されると、電力はポート1と2の間で均等に分割されますが、逆位相になりますが、ポート3には出力がありません。したがって、$ S_ {34} $ = 0 。
信号がポート3で供給される場合、電力はポート1と2の間で均等に分割されますが、ポート4では出力がありません。したがって、$ S_ {43} $ = 0です。
信号が同一線上のポートの1つに供給される場合、Eアームは位相遅延を生成し、Hアームは位相進みを生成するため、他の同一線上のポートには出力が表示されません。したがって、$ S_ {12} $ = $ S_ {21} $ = 0です。

EHプレーンティーの特性

EH Plane Teeのプロパティは、その$ \ left [S \ right] _ {4 \ times 4} $行列で定義できます。

4つの可能な入力と4つの可能な出力があるため、これは4×4の行列です。

$ [S] = \ begin {bmatrix} S_ {11}＆S_ {12}＆S_ {13}＆S_ {14} \\ S_ {21}＆S_ {22}＆S_ {23}＆S_ {24} \\ S_ {31}＆S_ {32}＆S_ {33}＆S_ {34} \\ S_ {41}＆S_ {42}＆S_ {43}＆S_ {44} \ end {bmatrix} $ ........ Equation 1

Hプレーンティーセクションがあるので

$ S_ {23} = S_ {13} $........ Equation 2

E-PlaneTeeセクションがあるので

$ S_ {24} = -S_ {14} $........ Equation 3

E-ArmポートとH-Armポートは非常に分離されているため、一方に入力が適用された場合、もう一方は出力を提供しません。したがって、これは次のように注意できます。

$ S_ {34} = S_ {43} = 0 $........ Equation 4

対称性から、

$ S_ {ij} = S_ {ji} $

$ S_ {12} = S_ {21}、S_ {13} = S_ {31}、S_ {14} = S_ {41} $

$ S_ {23} = S_ {32}、S_ {24} = S_ {42}、S_ {34} = S_ {43} $........ Equation 5

ポート3と4がジャンクションに完全に一致している場合、

$ S_ {33} = S_ {44} = 0 $........ Equation 6

上記のすべての式を式1に代入して、$ [S] $行列を取得します。

$ [S] = \ begin {bmatrix} S_ {11}＆S_ {12}＆S_ {13}＆S_ {14} \\ S_ {12}＆S_ {22}＆S_ {13}＆-S_ {14 } \\ S_ {13}＆S_ {13}＆0＆0 \\ S_ {14}＆-S_ {14}＆0＆0 \ end {bmatrix} $........ Equation 7

ユニタリプロパティから、$ [S] [S] ^ \ ast = [I] $

$ \ begin {bmatrix} S_ {11}＆S_ {12}＆S_ {13}＆S_ {14} \\ S_ {12}＆S_ {22}＆S_ {13}＆-S_ {14} \\ S_ {13}＆S_ {13}＆0＆0 \\ S_ {14}＆-S_ {14}＆0＆0 \ end {bmatrix} \ begin {bmatrix} S_ {11} ^ {*}＆S_ {12} ^ {*}＆S_ {13} ^ {*}＆S_ {14} ^ {*} \\ S_ {12} ^ {*}＆S_ {22} ^ {*}＆S_ {13} ^ {*}＆ -S_ {14} ^ {*} \\ S_ {13}＆S_ {13}＆0＆0 \\ S_ {14}＆-S_ {14}＆0＆0 \ end {bmatrix} $

$ = \ begin {bmatrix} 1＆0＆0＆0 \\ 0＆1＆0＆0 \\ 0＆0＆1＆0 \\ 0＆0＆0＆1 \ end {bmatrix} $

$ R_1C_1：\ left | S_ {11} \ right | ^ 2 + \ left | S_ {12} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 + \ left | S_ {14} \ right | ^ 2 = 1 $......... Equation 8

$ R_2C_2：\ left | S_ {12} \ right | ^ 2 + \ left | S_ {22} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 + \ left | S_ {14} \ right | ^ 2 = 1 $......... Equation 9

$ R_3C_3：\ left | S_ {13} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 $......... Equation 10

$ R_4C_4：\ left | S_ {14} \ right | ^ 2 + \ left | S_ {14} \ right | ^ 2 = 1 $......... Equation 11

式10と11から、次のようになります。

$ S_ {13} = \ frac {1} {\ sqrt {2}} $........ Equation 12

$ S_ {14} = \ frac {1} {\ sqrt {2}} $........ Equation 13

式8と9を比較すると、次のようになります。

$ S_ {11} = S_ {22} $ ......... Equation 14

式12および13のこれらの値を使用すると、次のようになります。

$ \ left | S_ {11} \ right | ^ 2 + \ left | S_ {12} \ right | ^ 2 + \ frac {1} {2} + \ frac {1} {2} = 1 $

$ \ left | S_ {11} \ right | ^ 2 + \ left | S_ {12} \ right | ^ 2 = 0 $

$ S_ {11} = S_ {22} = 0 $ ......... Equation 15

式9から、$ S_ {22} = 0 $が得られます。 ......... Equation 16

これで、ポート1と2がジャンクションに完全に一致していることがわかりました。これは4ポートのジャンクションであるため、2つのポートが完全に一致する場合は常に、他の2つのポートもジャンクションに完全に一致します。

4つのポートすべてが完全に一致するジャンクションは、マジックティージャンクションと呼ばれます。

式7の$ [S] $行列に12から16までの式を代入することにより、MagicTeeの散乱行列を次のように取得します。

$$ [S] = \ begin {bmatrix} 0＆0＆\ frac {1} {2}＆\ frac {1} {\ sqrt {2}} \\ 0＆0＆\ frac {1} {2}＆-\ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}}＆\ frac {1} {\ sqrt {2}}＆0＆0 \\ \ frac {1} {\ sqrt {2}}＆-\ frac {1} {\ sqrt {2}}＆0＆0 \ end {bmatrix} $$

$ [b] $ = $ [S] [a] $であることはすでにわかっています

上記を書き直すと、

$$ \ begin {vmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \ end {vmatrix} = \ begin {bmatrix} 0＆0＆\ frac {1} {2}＆\ frac {1} {\ sqrt {2} } \\ 0＆0＆\ frac {1} {2}＆-\ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}}＆\ frac {1} {\ sqrt {2}}＆0＆0 \\ \ frac {1} {\ sqrt {2}}＆-\ frac {1} {\ sqrt {2}}＆0＆0 \ end {bmatrix} \ begin {vmatrix} a_1 \ \ a_2 \\ a_3 \\ a_4 \ end {vmatrix} $$

EHプレーンティーの用途

EH PlaneTeeの最も一般的なアプリケーションのいくつかは次のとおりです。

EHプレーンジャンクションはインピーダンスの測定に使用されます-ヌル検出器はE-Armポートに接続され、マイクロ波ソースはH-Armポートに接続されます。同一線上のポートとこれらのポートがブリッジを形成し、インピーダンス測定はブリッジのバランスをとることによって行われます。
EH Plane Teeはデュプレクサとして使用されます-デュプレクサは、両方の目的に単一のアンテナを使用して、送信機と受信機の両方として機能する回路です。ポート1と2は、それらが分離されているため干渉しない受信機と送信機として使用されます。アンテナはE-Armポートに接続されています。整合した負荷がH-Armポートに接続されており、反射はありません。現在、問題なく送受信があります。
EH Plane Teeはミキサーとして使用されます-E-Armポートはアンテナに接続され、H-Armポートは局部発振器に接続されます。ポート2には反射のない整合負荷があり、ポート1にはミキサー回路があります。ミキサー回路は信号電力の半分と発振器電力の半分を取得してIF周波数を生成します。

上記のアプリケーションに加えて、EHプレーンティージャンクションは、マイクロ波ブリッジ、マイクロ波弁別器などとしても使用されます。