マイクロ波工学-マグネトロン

これまでに説明したチューブとは異なり、マグネトロンは、電界と磁界が交差する、つまり互いに垂直に走るクロスフィールドチューブです。TWTでは、電子がRFと相互作用するようにすると、クライストロンよりも長時間、効率が高くなることが観察されました。マグネトロンでも同じ手法が採用されています。

マグネトロンの種類

マグネトロンには主に3つのタイプがあります。

負性抵抗タイプ

2つのアノードセグメント間の負性抵抗が使用されます。
それらは効率が低い。
これらは低周波数（<500 MHz）で使用されます。

サイクロトロン周波数マグネトロン

電気成分と振動電子の間の同期が考慮されます。
100MHzより高い周波数に役立ちます。

進行波またはキャビティタイプ

電子と回転電磁場の間の相互作用が考慮されます。
高ピーク電力振動が提供されます。
レーダーアプリケーションで役立ちます。

キャビティマグネトロン

マグネトロンは、アノードが共振空洞になり、永久磁石が強力な磁場を生成するために使用され、これらの両方の作用によってデバイスが機能するため、空洞マグネトロンと呼ばれます。

キャビティマグネトロンの構築

厚い円筒形の陰極が中央にあり、銅の円筒形のブロックが軸方向に固定されており、陽極として機能します。このアノードブロックは、共振アノードキャビティとして機能するいくつかのスロットで構成されています。

アノードとカソードの間に存在する空間は、 Interaction space。電場は半径方向に存在し、磁場はキャビティマグネトロンに軸方向に存在します。この磁場は、磁力線が陰極に平行で、陽極と陰極の間に存在する電場に垂直になるように配置された永久磁石によって生成されます。

次の図は、キャビティマグネトロンの構造の詳細と、軸方向に存在する磁束の磁力線を示しています。

このキャビティマグネトロンには、互いに緊密に結合された8つのキャビティがあります。Nキャビティマグネトロンには$ N $の動作モードがあります。これらの動作は、振動の周波数と位相に依存します。この空洞共振器のリングの周りの合計位相シフトは$ 2n \ pi $である必要があります。ここで、$ n $は整数です。

$ \ phi_v $が、隣接するキャビティ間のAC電界の相対的な相変化を表す場合、

$$ \ phi_v = \ frac {2 \ pi n} {N} $$

ここで、$ n = 0、\：\ pm1、\：\ pm2、\：\ pm \：（\ frac {N} {2} -1）、\：\ pm \ frac {N} {2} $

つまり、$ N $が偶数の場合、$ \ frac {N} {2} $モードの共振が存在する可能性があります。

もし、

$$ n = \ frac {N} {2} \ quad then \ quad \ phi_v = \ pi $$

この共振モードは$ \ pi-mode $と呼ばれます。

$$ n = 0 \ quad、次に\ quad \ phi_v = 0 $$

これは、 Zero mode、アノードとカソードの間にRF電界がないためです。これは、Fringing Field このモードはマグネトロンでは使用されません。

キャビティマグネトロンの操作

キャビティクライストロンが稼働しているときは、考慮すべきさまざまなケースがあります。それらについて詳しく見ていきましょう。

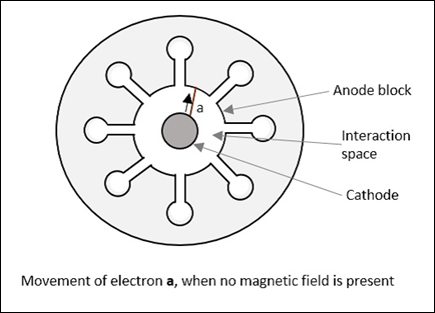
Case 1

磁場がない場合、つまりB = 0の場合、次の図で電子の振る舞いを観察できます。例を考えると、ここで電子a 半径方向の電気力の下で直接アノードに行きます。

Case 2

磁場が増加すると、横方向の力が電子に作用します。これは、電子を考慮して、次の図で観察できます。b 両方の力がそれに作用している間、それは湾曲した経路を取ります。

このパスの半径は次のように計算されます

$$ R = \ frac {mv} {eB} $$

これは電子の速度に比例して変化し、磁場の強さに反比例します。

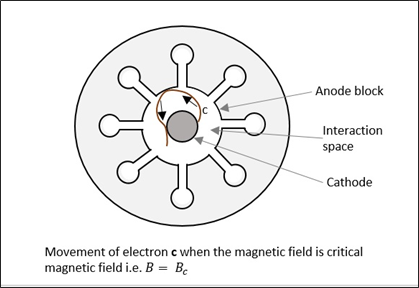
Case 3

磁場の場合 B さらに増加すると、電子は電子などの経路をたどります c、アノード表面をかすめ、アノード電流をゼロにするだけです。これは「Critical magnetic field"$（B_c）$、これはカットオフ磁場です。理解を深めるために次の図を参照してください。

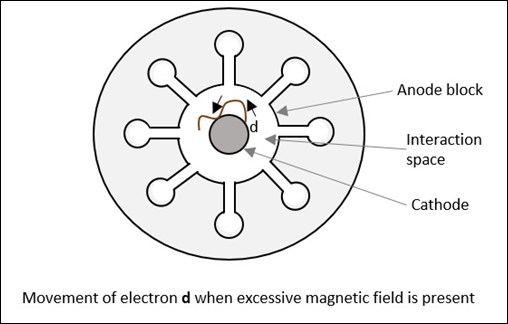
Case 4

磁場を臨界磁場より大きくすると、

$$ B> B_c $$

次に、電子は電子として経路をたどります d、電子はアノードに行かずにカソードにジャンプして戻ります。これは〜をひき起こす "back heating陰極の "。次の図を参照してください。

これは、発振が始まったら電源を切ることで実現します。これを続けると、陰極の発光効率に影響が出ます。

アクティブRFフィールドを備えたキャビティマグネトロンの動作

これまで、マグネトロンの空洞にRF磁場が存在しない空洞マグネトロンの動作について説明してきました（静的な場合）。ここで、アクティブなRFフィールドがある場合の動作について説明します。

TWTの場合と同様に、一時的なノイズが原因で、最初のRF振動が存在すると仮定します。振動は、デバイスの操作によって維持されます。この過程で放出される電子には3種類あり、その作用は電子として理解されます。a、 b そして c、3つの異なる場合。

Case 1

振動が存在する場合、電子 a、振動するエネルギーの伝達を遅くします。エネルギーを振動に伝達するこのような電子は、favored electrons。これらの電子はbunching effect。

Case 2

この場合、別の電子、 b、振動からエネルギーを取り、その速度を上げます。これが行われると、

より鋭く曲がります。
インタラクションスペースで過ごす時間はほとんどありません。
陰極に戻ります。

これらの電子は unfavored electrons。それらはバンチング効果には関与しません。また、これらの電子は「逆熱」を引き起こすため、有害です。

Case 3

この場合、電子 c少し遅れて放出される、より速く動きます。電子に追いつけようとするa。次に放出される電子d、と歩こうとします a。その結果、優先電子a、 c そして d電子束または電子雲を形成します。それを「位相集束効果」と呼びました。

このプロセス全体は、次の図を見るとよく理解できます。

図Aはさまざまな場合の電子の動きを示し、図Bは形成された電子雲を示しています。これらの電子雲は、デバイスの動作中に発生します。これらのアノードセグメントの内面に存在する電荷は、キャビティ内の振動に従います。これにより、時計回りに回転する電界が発生し、実際の実験中に実際に見ることができます。

電界が回転している間、磁束線はカソードに平行に形成され、その複合効果の下で、電子バンチは、らせん軌道で最も近い正のアノードセグメントに一定の間隔で向けられた4本のスポークで形成されます。