VLSI設計-MOSトランジスタ
相補型MOSFET(CMOS)テクノロジは、今日、さまざまなアプリケーションで回路を形成するために広く使用されています。今日のコンピューター、CPU、および携帯電話は、いくつかの重要な利点のためにCMOSを利用しています。CMOSは、両方の状態で低消費電力、比較的高速、高ノイズマージンを提供し、広範囲のソース電圧と入力電圧で動作します(ソース電圧が固定されている場合)。
ここで説明するプロセスでは、使用可能なトランジスタのタイプは、金属-酸化物-半導体電界効果トランジスタ(MOSFET)です。これらのトランジスタが形成されますas a ‘sandwich’シリコンの単結晶からの半導体層、通常はスライスまたはウェーハからなる。二酸化ケイ素(酸化物)の層と金属の層。
MOSFETの構造
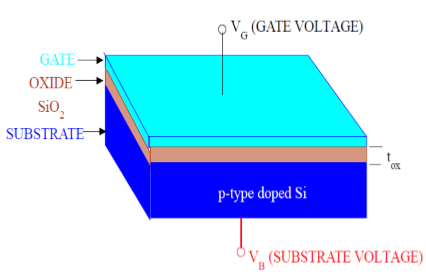
図に示すように、MOS構造には3つの層が含まれています-
The Metal Gate Electrode
The Insulating Oxide Layer (SiO2)
P – type Semiconductor (Substrate)
MOS構造はコンデンサを形成し、ゲートと基板は2つのプレートであり、酸化物層は誘電体材料です。誘電体(SiO 2)の厚さは通常10 nm〜50nmです。基板内のキャリア濃度と分布は、ゲートと基板端子に印加される外部電圧によって操作できます。ここで、MOSの構造を理解するために、まずP型半導体基板の基本的な電気的特性を検討します。
半導体材料中のキャリアの濃度は常に次のとおりです。 Mass Action Law。質量作用の法則は次の式で与えられます-
$$ np = n_ {i} ^ {2} $$
どこ、
n 電子のキャリア濃度です
p は正孔のキャリア濃度です
ni シリコンの固有のキャリア濃度です
今基板が等しくアクセプタ(ホウ素)濃度Nがドープされていると仮定するA。したがって、p型基板の電子と正孔の濃度は
$$ n_ {po} = \ frac {n_ {i} ^ {2}} {N_ {A}} $$
$$ p_ {po} = N_ {A} $$
ここでは、ドーピング濃度 NA(10 15 10へ16 cmで-3)真性濃度NIよりも大きいです。ここで、MOS構造を理解するために、p型シリコン基板のエネルギー準位図を検討します。
図に示すように、伝導帯と価電子帯のバンドギャップは1.1eVです。ここでは、フェルミポテンシャルΦ Fは真性フェルミ準位(Eとの差であるI)とフェルミ準位(E FP)。
どこフェルミ準位E Fは、ドーピング濃度に依存します。フェルミポテンシャルΦ Fは真性フェルミ準位(Eとの差であるI)とフェルミ準位(E FP)。
数学的には、
$$ \ Phi_ {Fp} = \ frac {E_ {F} -E_ {i}} {q} $$
伝導帯と自由空間の電位差は電子親和力と呼ばれ、qxで表されます。
だから、フリースペースにフェルミレベルから移動する電子のために必要なエネルギーは、仕事関数(qΦと呼ばれているS)と、それは次式で与えられます。
$$ q \ Phi _ {s} =(E_ {c} -E_ {F})+ qx $$
次の図は、MOSを構成するコンポーネントのエネルギーバンド図を示しています。
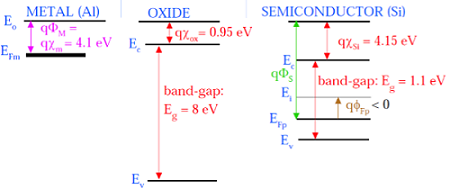
上図に示すように、絶縁性のSiO 2層は8eVの大きなエネルギーバンドギャップを持ち、仕事関数は0.95eVです。金属ゲートの仕事関数は4.1eVです。ここでは、仕事関数が異なるため、MOSシステム全体で電圧降下が発生します。下の図は、MOSシステムの結合エネルギーバンド図を示しています。
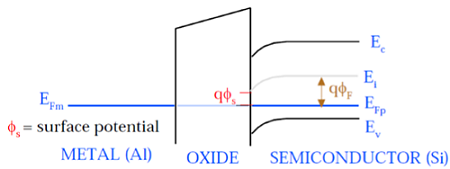
この図に示すように、金属ゲートと半導体(Si)のフェルミ準位は同じ電位です。表面のフェルミ電位は表面電位Φと呼ばれるS、それはフェルミポテンシャルΦよりも小さいF大きさインチ
MOSFETの動作
MOSFETは、チャネル領域の近くに配置された2つのpn接合を備えたMOSコンデンサで構成され、この領域はゲート電圧によって制御されます。両方のpn接合を逆バイアスにするために、基板電位は他の3つの端子電位よりも低く保たれます。
ゲート電圧がしきい値電圧を超えて上昇すると(V GS > V TO)、表面に反転層が確立され、ソースとドレインの間にn型チャネルが形成されます。このn型チャネルは、VDS値に従ってドレイン電流を流します。
V DSの値が異なる場合、MOSFETは以下で説明するように異なる領域で動作できます。
線形領域
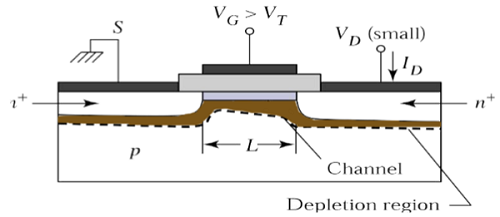
V DS = 0では、熱平衡が反転チャネル領域に存在し、ドレイン電流I D = 0です。ここで、小さなドレイン電圧V DS > 0が印加されると、VDSに比例するドレイン電流がソースからチャネルから排出します。
チャネルは、ソースからドレインへの電流の流れのための連続的なパスを提供します。この動作モードはと呼ばれますlinear region。線形領域で動作するnチャネルMOSFETの断面図を次の図に示します。
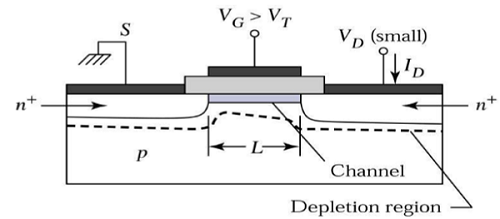
飽和領域の端に
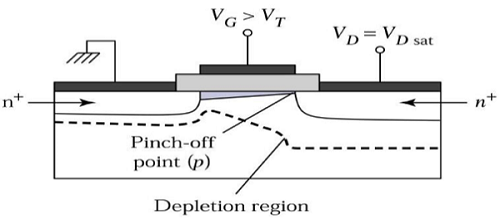
ここで、V DSを増やすと、チャネル内の電荷とチャネルの深さがドレインの終わりで減少します。V DS = V DSATの場合、チャネルの電荷はゼロに減少します。これは、pinch – off point。飽和領域のエッジで動作するnチャネルMOSFETの断面図を次の図に示します。
飽和領域
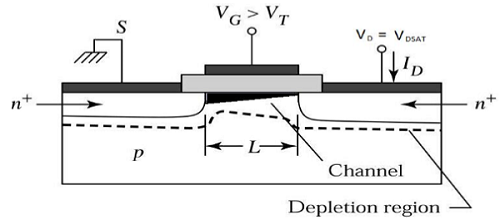
V DS > V DSATの場合、空乏化した表面がドレインの近くに形成され、ドレイン電圧を上げることにより、この空乏化した領域がソースまで広がります。
この動作モードはと呼ばれます Saturation region。ソースからチャネル端に来る電子は、ドレイン-空乏領域に入り、高電界でドレインに向かって加速されます。
MOSFET電流–電圧特性
MOSFETの電流-電圧特性を理解するために、チャネルの近似が行われます。この近似がないと、MOSシステムの3次元解析が複雑になります。ザ・Gradual Channel Approximation (GCA) 電流-電圧特性の場合、分析の問題が軽減されます。
段階的チャネル近似(GCA)
線形モードで動作するnチャネルMOSFETの断面図を考えてみましょう。ここでは、ソースと基板がグランドに接続されています。V S = V B = 0ゲート-へ-ソース(V GS)とドレイン-へ-ソース電圧(V DS)の電圧がドレイン電流I制御する外部パラメータであるDは。
電圧、V GSが閾値電圧Vよりも大きな電圧に設定されているTOソースとドレイン間のチャネルを作成します。図に示すように、x –方向は表面に垂直で、y –方向は表面に平行です。
ここで、図に示すように、ソース端でy = 0です。ソースに対するチャネル電圧は、次の式で表されます。VC(Y)。閾値電圧VTOは、チャネル電圧Vの境界条件Yにチャネル領域、yと= 0に沿って一定= Lであると仮定Cれています-
$$ V_ {c} \ left(y = 0 \ right)= V_ {s} = 0 \、and \、V_ {c} \ left(y = L \ right)= V_ {DS} $$
また、
$$ V_ {GS} \ geq V_ {TO} $$および
$$ V_ {GD} = V_ {GS} -V_ {DS} \ geq V_ {TO} $$
Q1(y)を表面反転層の総可動電子電荷とします。この電子電荷は次のように表すことができます。
$$ Q1(y)=-C_ {ox}。[V_ {GS} -V_ {C(Y)}-V_ {TO}] $$
下の図は、表面反転層の空間ジオメトリを示し、その寸法を示しています。ドレインからソースに移動すると、反転層は次第に減少します。ここで、チャネル長Lの小さな領域dyを考慮すると、この領域によって提供される増分抵抗dRは次のように表すことができます。
$$ dR =-\ frac {dy} {w。\ mu _ {n} .Q1(y)} $$
ここで、マイナス符号は、反転層の電荷Q1とμの負極性によるものでnは定数である表面移動度です。ここで、dR方程式のQ1(y)の値を代入します-
$$ dR =-\ frac {dy} {w。\ mu _ {n}。\ left \ {-C_ {ox} \ left [V_ {GS} -V_ {C \ left(Y \ right)} \ right ] -V_ {TO} \ right \}} $$
$$ dR = \ frac {dy} {w。\ mu _ {n} .C_ {ox} \ left [V_ {GS} -V_ {C \ left(Y \ right)} \ right] -V_ {TO} } $$
これで、小さなdy領域での電圧降下は次の式で与えられます。
$$ dV_ {c} = I_ {D} .dR $$
dRの値を上記の式に入れます
$$ dV_ {C} = I_ {D}。\ frac {dy} {w。\ mu_ {n} .C_ {ox} \ left [V_ {GS} -V_ {C(Y)} \ right] -V_ {TO}} $$
$$ w。\ mu _ {n} .C_ {ox} \ left [V_ {GS} -V_ {C(Y)}-V_ {TO} \ right] .dV_ {C} = I_ {D} .dy $$
チャネル領域全体にわたるドレイン電流IDを取得するには、上記の式をチャネルに沿ってy = 0からy = Lまで、電圧V C(y) = 0からVC (y) = VDSまで積分できます。
$$ C_ {ox} .w。\ mu _ {n}。\ int_ {V_ {c} = 0} ^ {V_ {DS}} \ left [V_ {GS} -V_ {C \ left(Y \ right )}-V_ {TO} \ right] .dV_ {C} = \ int_ {Y = 0} ^ {L} I_ {D} .dy $$
$$ \ frac {C_ {ox} .w。\ mu _ {n}} {2} \ left(2 \ left [V_ {GS} -V_ {TO} \ right] V_ {DS} -V_ {DS} ^ {2} \ right)= I_ {D} \ left [L-0 \ right] $$
$$ I_ {D} = \ frac {C_ {ox}。\ mu _ {n}} {2}。\ frac {w} {L} \ left(2 \ left [V_ {GS} -V_ {TO} \ right] V_ {DS} -V_ {DS} ^ {2} \ right)$$
線形領域の場合VDS <V GS − VTO。飽和領域の場合、V DSの値は(V GS − V TO)よりも大きくなります。したがって、飽和領域の場合、V DS =(V GS − V TO)。
$$ I_ {D} = C_ {ox}。\ mu _ {n}。\ frac {w} {2} \ left(\ frac {\ left [2V_ {DS} \ right] V_ {DS} -V_ { DS} ^ {2}} {L} \ right)$$
$$ I_ {D} = C_ {ox}。\ mu _ {n}。\ frac {w} {2} \ left(\ frac {2V_ {DS} ^ {2} -V_ {DS} ^ {2} } {L} \ right)$$
$$ I_ {D} = C_ {ox}。\ mu _ {n}。\ frac {w} {2} \ left(\ frac {V_ {DS} ^ {2}} {L} \ right)$$
$$ I_ {D} = C_ {ox}。\ mu _ {n}。\ frac {w} {2} \ left(\ frac {\ left [V_ {GS} -V_ {TO} \ right] ^ { 2}} {L} \ right)$$