VLSI設計-クイックガイド

超大規模集積回路（VLSI）は、 integrated circuit （IC）数千を組み合わせることによって transistorsシングルチップに。VLSIは1970年代に複雑になったときに始まりましたsemiconductor そして communication技術が開発されていました。ザ・microprocessor VLSIデバイスです。

VLSI技術が導入される前は、ほとんどのICは実行できる機能のセットが限られていました。アンelectronic circuit で構成されている可能性があります CPU, ROM, RAM およびその他 glue logic。VLSIを使用すると、IC設計者はこれらすべてを1つのチップに追加できます。

エレクトロニクス業界は、主に大規模な統合技術とシステム設計アプリケーションの急速な進歩により、過去数十年にわたって驚異的な成長を遂げてきました。超大規模集積回路（VLSI）設計の出現により、高性能コンピューティング、制御、電気通信、画像およびビデオ処理、および家庭用電化製品における集積回路（IC）のアプリケーションの数は非常に速いペースで増加しています。

高解像度、低ビットレートのビデオおよびセルラー通信などの現在の最先端技術は、エンドユーザーに驚異的な量のアプリケーション、処理能力、および移植性を提供します。この傾向は急速に拡大すると予想され、VLSI設計とシステム設計に非常に重要な影響を及ぼします。

VLSI設計フロー

VLSIIC回路の設計フローを下図に示します。設計のさまざまなレベルに番号が付けられ、ブロックは設計フローのプロセスを示しています。

仕様が最初に来て、それらは設計されるデジタルIC回路の機能、インターフェース、およびアーキテクチャを抽象的に説明します。

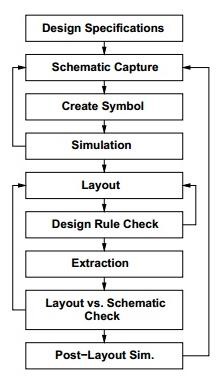
次に、動作の説明が作成され、機能、パフォーマンス、特定の標準への準拠、およびその他の仕様の観点から設計が分析されます。

RTLの記述はHDLを使用して行われます。このRTL記述は、機能をテストするためにシミュレートされています。ここから先は、EDAツールの助けが必要です。

次に、RTL記述は、論理合成ツールを使用してゲートレベルのネットリストに変換されます。ゲートレベルのネットリストは、ゲートとゲート間の接続に関する回路の説明であり、タイミング、電力、およびエリアの仕様を満たすように作成されています。

最後に、物理的なレイアウトが作成され、検証されてから製造に送られます。

Yチャート

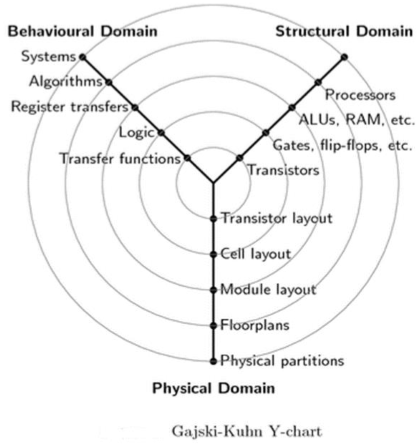
Gajski-Kuhn Yチャートは、半導体デバイスを設計する際の考慮事項を捉えたモデルです。

Gajski-Kuhn Yチャートの3つのドメインは、放射軸上にあります。各ドメインは、同心円状のリングを使用して、抽象化のレベルに分割できます。

トップレベル（外輪）では、チップのアーキテクチャを検討します。下位レベル（内輪）では、設計を次々と改良して、より詳細な実装にします。

動作記述から構造記述を作成することは、高位合成または論理合成のプロセスを通じて実現されます。

構造的な記述から物理的な記述を作成することは、レイアウト合成によって実現されます。

設計階層-構造

設計階層には、「分割統治」の原則が含まれます。最も単純なレベルに達するまで、タスクをより小さなタスクに分割することに他なりません。このプロセスは、設計の最後の進化が非常に単純になり、製造が容易になるため、最も適しています。

与えられたタスクを設計フロープロセスのドメイン（動作、構造、および幾何学的）に設計できます。これを理解するために、次の図に示すように、16ビット加算器を設計する例を見てみましょう。

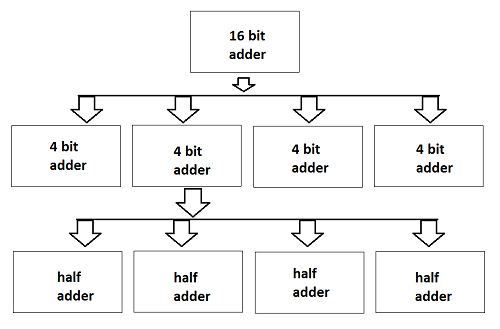
ここでは、16ビット加算器のチップ全体が4ビット加算器の4つのモジュールに分割されています。さらに、4ビット加算器を1ビット加算器または半加算器に分割します。1ビットの加算は最も単純な設計プロセスであり、その内部回路もチップ上で簡単に製造できます。これで、最後の4つの加算器すべてを接続して、4ビット加算器を設計できます。次に進むと、16ビット加算器を設計できます。

FPGA –はじめに

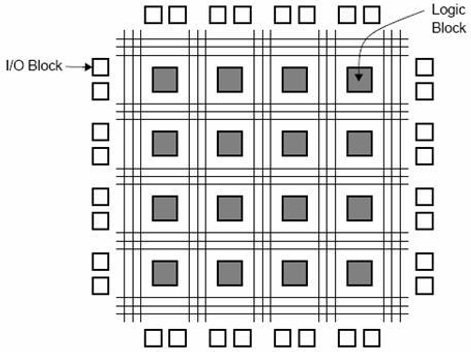
の完全な形式 FPGA は「Field Programmable Gate Array」。プログラム可能な相互接続を備えた1万から100万を超える論理ゲートが含まれています。プログラム可能な相互接続は、ユーザーまたは設計者が特定の機能を簡単に実行するために利用できます。典型的なモデルのFPGAチップを図に示します。機能に応じて設計および番号付けされたI / Oブロックがあります。論理レベル構成の各モジュールには、CLB’s (Configurable Logic Blocks)。

CLBは、モジュールに与えられた論理演算を実行します。CLBブロックとI / Oブロック間の相互接続は、水平ルーティングチャネル、垂直ルーティングチャネル、およびPSM（プログラマブルマルチプレクサ）を使用して行われます。

含まれるCLBの数は、FPGAの複雑さを決定するだけです。CLBおよびPSMの機能は、VHDLまたはその他のハードウェア記述言語によって設計されています。プログラミング後、CLBとPSMはチップ上に配置され、ルーティングチャネルで相互に接続されます。

利点

• 非常に短い時間で済みます。設計プロセスから機能チップまで。
• 物理的な製造ステップは含まれていません。
• 唯一の欠点は、他のスタイルよりもコストがかかることです。

ゲートアレイ設計

ザ・ gate array (GA)ラピッドプロトタイピング機能の点で、FPGAに次ぐランクです。FPGAチップのデザイン実装にはユーザープログラミングが重要ですが、GAにはメタルマスクのデザインと処理が使用されます。ゲートアレイの実装には、2段階の製造プロセスが必要です。

最初のフェーズでは、各GAチップ上にコミットされていないトランジスタのアレイが生成されます。これらのコミットされていないチップは、後でカスタマイズするために保存できます。これは、アレイのトランジスタ間の金属相互接続を定義することで完了します。金属相互接続のパターン化はチップ製造プロセスの最後に行われるため、ターンアラウンドタイムは数日から数週間と短くなります。次の図は、ゲートアレイ実装の基本的な処理手順を示しています。

一般的なゲートアレイプラットフォームは、MOSトランジスタの行または列間のセル間ルーティングにチャネルと呼ばれる専用領域を使用します。それらは相互接続を簡素化します。基本的な論理ゲートを実行する相互接続パターンはライブラリに格納され、ネットリストに従ってコミットされていないトランジスタの行をカスタマイズするために使用できます。

最新のGAのほとんどでは、チャネルルーティングに複数の金属層が使用されています。複数の相互接続された層を使用することで、アクティブセルエリア上でルーティングを実現できます。Sea-of-Gates（SOG）チップのようにルーティングチャネルを削除できるようにします。ここでは、チップ表面全体がコミットされていないnMOSおよびpMOSトランジスタで覆われています。隣接するトランジスタは、金属マスクを使用してカスタマイズし、基本的な論理ゲートを形成できます。

セル間ルーティングでは、コミットされていないトランジスタの一部を犠牲にする必要があります。この設計スタイルにより、相互接続の柔軟性が高まり、通常は密度が高くなります。GAチップ利用率は、使用チップ面積を総チップ面積で割って測定します。FPGAよりも高速で、チップ速度も高速です。

標準セルベースの設計

標準のセルベースの設計では、完全なカスタムマスクセットの開発が必要です。標準セルは、ポリセルとも呼ばれます。このアプローチでは、一般的に使用されるすべてのロジックセルが開発され、特性評価され、標準のセルライブラリに保存されます。

ライブラリには、インバータ、NANDゲート、NORゲート、複雑なAOI、OAIゲート、Dラッチ、フリップフロップなど、数百のセルが含まれる場合があります。各ゲートタイプは、さまざまなファンアウトに適切な駆動機能を提供するために、いくつかのバージョンで実装できます。インバータゲートは標準サイズ、2倍サイズ、4倍サイズにすることができるため、チップ設計者は適切なサイズを選択して、高い回路速度とレイアウト密度を得ることができます。

各セルは、次のようないくつかの異なる特性カテゴリに従って特性評価されます。

• 遅延時間と負荷容量
• 回路シミュレーションモデル
• タイミングシミュレーションモデル
• 故障シミュレーションモデル
• 配置配線のセルデータ
• マスクデータ

セルの自動配置とルーティングのために、各セルレイアウトは固定の高さで設計されているため、複数のセルを並べて境界を付けて行を形成できます。電源レールと接地レールは、セルの上限と下限に平行に走っています。そのため、隣接するセルは共通の電力バスと共通の地上バスを共有します。以下の図は、標準セルベースの設計のフロアプランです。

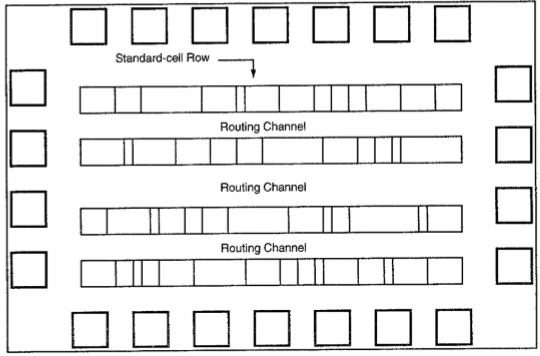
フルカスタムデザイン

フルカスタムデザインでは、ライブラリを使用せずにマスクデザイン全体が新しくなります。このデザインスタイルの開発コストは上昇しています。このように、設計の再利用の概念は、設計のサイクルタイムと開発コストを削減するために有名になりつつあります。

最も難しい完全なカスタム設計は、静的または動的のメモリセルの設計です。ロジックチップ設計の場合、同じチップ上で異なる設計スタイルの組み合わせ、つまり標準セル、データパスセル、およびを使用して、適切なネゴシエーションを得ることができます。programmable logic arrays (PLAs)。

実際には、設計者は完全なカスタムレイアウト、つまりすべてのトランジスタの形状、方向、配置を行います。通常、設計の生産性は非常に低くなります。通常、設計者1人あたり1日あたり数十個のトランジスタ。デジタルCMOSVLSIでは、人件費が高いため、フルカスタム設計はほとんど使用されていません。これらのデザインスタイルには、メモリチップ、高性能マイクロプロセッサ、FPGAなどの大量生産製品のデザインが含まれます。

相補型MOSFET（CMOS）テクノロジは、今日、さまざまなアプリケーションで回路を形成するために広く使用されています。今日のコンピューター、CPU、および携帯電話は、いくつかの重要な利点のためにCMOSを利用しています。CMOSは、両方の状態で低消費電力、比較的高速、高ノイズマージンを提供し、広範囲のソース電圧と入力電圧で動作します（ソース電圧が固定されている場合）。

ここで説明するプロセスでは、使用可能なトランジスタのタイプは、金属酸化物半導体電界効果トランジスタ（MOSFET）です。これらのトランジスタが形成されますas a ‘sandwich’シリコンの単結晶からの半導体層、通常はスライスまたはウェーハからなる。二酸化ケイ素（酸化物）の層と金属の層。

MOSFETの構造

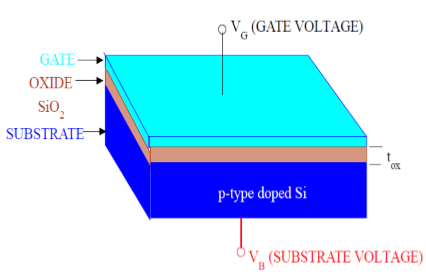
図に示すように、MOS構造には3つの層が含まれています-

• The Metal Gate Electrode

• The Insulating Oxide Layer (SiO₂)

• P – type Semiconductor (Substrate)

MOS構造はコンデンサを形成し、ゲートと基板は2つのプレートであり、酸化物層は誘電体材料です。誘電体（SiO ₂）の厚さは通常10 nm〜50nmです。基板内のキャリア濃度と分布は、ゲートと基板端子に印加される外部電圧によって操作できます。ここで、MOSの構造を理解するために、まずP型半導体基板の基本的な電気的特性を検討します。

半導体材料中のキャリアの濃度は常に次のとおりです。 Mass Action Law。質量作用の法則は次の式で与えられます-

$$n.p=n_{i}^{2}$$

どこ、

• n 電子のキャリア濃度です

• p は正孔のキャリア濃度です

• n_i はシリコンの固有キャリア濃度です

今基板が等しくアクセプタ（ホウ素）濃度Nがドープされていると仮定する_A。したがって、p型基板の電子と正孔の濃度は

$$n_{po}=\frac{n_{i}^{2}}{N_{A}}$$

$$p_{po}=N_{A}$$

ここでは、ドーピング濃度 N_A（10 ¹⁵ 10へ¹⁶ cmで^-3）真性濃度NIよりも大きいです。ここで、MOS構造を理解するために、p型シリコン基板のエネルギー準位図を検討します。

図に示すように、伝導帯と価電子帯のバンドギャップは1.1eVです。ここでは、フェルミポテンシャルΦ _Fは真性フェルミ準位（Eとの差である_I）とフェルミ準位（E _FP）。

どこフェルミ準位E _Fは、ドーピング濃度に依存します。フェルミポテンシャルΦ _Fは真性フェルミ準位（Eとの差である_I）とフェルミ準位（E _FP）。

数学的には、

$$\Phi_{Fp}=\frac{E_{F}-E_{i}}{q}$$

伝導帯と自由空間の電位差は電子親和力と呼ばれ、qxで表されます。

だから、フリースペースにフェルミレベルから移動する電子のために必要なエネルギーは、仕事関数（qΦと呼ばれている_S）と、それは次式で与えられます。

$$q\Phi _{s}=(E_{c}-E_{F})+qx$$

次の図は、MOSを構成するコンポーネントのエネルギーバンド図を示しています。

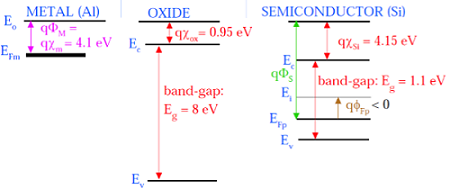
上図に示すように、絶縁性のSiO ₂層は8eVの大きなエネルギーバンドギャップを持ち、仕事関数は0.95eVです。金属ゲートの仕事関数は4.1eVです。ここでは、仕事関数が異なるため、MOSシステム全体で電圧降下が発生します。下の図は、MOSシステムの結合エネルギーバンド図を示しています。

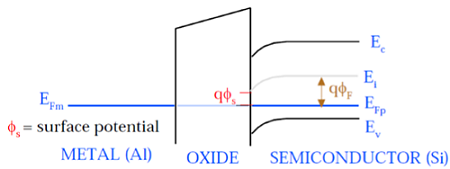
この図に示すように、金属ゲートと半導体（Si）のフェルミ準位は同じ電位です。表面のフェルミ電位は表面電位Φと呼ばれる_S、それはフェルミポテンシャルΦよりも小さい_F大きさインチ

MOSFETの動作

MOSFETは、チャネル領域の近くに配置された2つのpn接合を備えたMOSコンデンサで構成され、この領域はゲート電圧によって制御されます。両方のpn接合を逆バイアスにするために、基板電位は他の3つの端子電位よりも低く保たれます。

ゲート電圧がしきい値電圧を超えて上昇すると（V _GS > V _TO）、表面に反転層が確立され、ソースとドレインの間にn型チャネルが形成されます。このn型チャネルは、_VDS値に従ってドレイン電流を流します。

V _DSの値が異なる場合、MOSFETは以下で説明するように異なる領域で動作できます。

線形領域

V _DS = 0では、熱平衡が反転チャネル領域に存在し、ドレイン電流I _D = 0です。ここで、小さなドレイン電圧V _DS > 0が印加されると、_VDSに比例するドレイン電流がソースからチャネルから排出します。

チャネルは、ソースからドレインへの電流の流れのための連続的なパスを提供します。この動作モードはと呼ばれますlinear region。線形領域で動作するnチャネルMOSFETの断面図を次の図に示します。

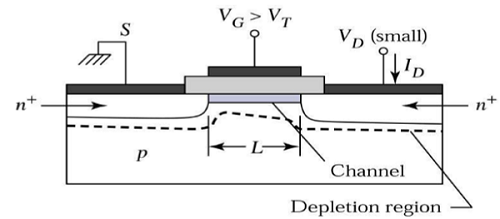
飽和領域の端に

ここで、V _DSを増やすと、チャネル内の電荷とチャネルの深さがドレインの終わりで減少します。V _DS = V _DSATの場合、チャネルの電荷はゼロに減少します。これは、pinch – off point。飽和領域のエッジで動作するnチャネルMOSFETの断面図を次の図に示します。

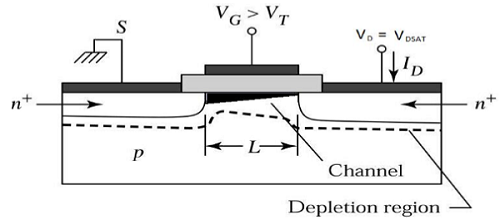
飽和領域

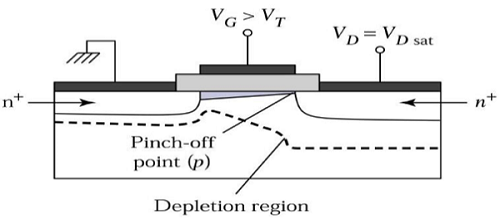
V _DS > V _DSATの場合、空乏化した表面がドレインの近くに形成され、ドレイン電圧を上げることにより、この空乏化した領域がソースまで広がります。

この動作モードはと呼ばれます Saturation region。ソースからチャネル端に来る電子は、ドレイン-空乏領域に入り、高電界でドレインに向かって加速されます。

MOSFET電流–電圧特性

MOSFETの電流-電圧特性を理解するために、チャネルの近似が行われます。この近似がないと、MOSシステムの3次元解析が複雑になります。ザ・Gradual Channel Approximation (GCA) 電流-電圧特性の場合、分析の問題が軽減されます。

段階的チャネル近似（GCA）

線形モードで動作するnチャネルMOSFETの断面図を考えてみましょう。ここでは、ソースと基板がグランドに接続されています。V _S = V _B = 0ゲート-へ-ソース（V _GS）とドレイン-へ-ソース電圧（V _DS）の電圧がドレイン電流I制御する外部パラメータである_Dは。

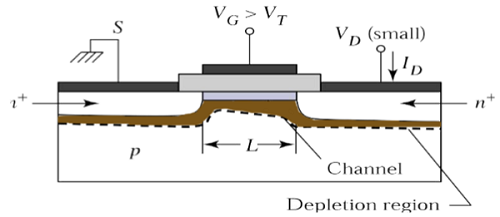
電圧、V _GSが閾値電圧Vよりも大きな電圧に設定されている_TOソースとドレイン間のチャネルを作成します。図に示すように、x –方向は表面に垂直で、y –方向は表面に平行です。

ここで、図に示すように、ソース端でy = 0です。ソースに対するチャネル電圧は、次の式で表されます。V_C(Y)。閾値電圧VTOは、チャネル電圧Vの境界条件Yにチャネル領域、yと= 0に沿って一定= Lであると仮定_Cれています-

$$V_{c}\left ( y = 0 \right ) = V_{s} = 0 \,and\,V_{c}\left ( y = L \right ) = V_{DS}$$

また、

$$V_{GS}\geq V_{TO}$$ そして

$$V_{GD} = V_{GS}-V_{DS}\geq V_{TO}$$

Q1（y）を表面反転層の総可動電子電荷とします。この電子電荷は次のように表すことができます。

$$Q1(y)=-C_{ox}.[V_{GS}-V_{C(Y)}-V_{TO}]$$

下の図は、表面反転層の空間ジオメトリを示し、その寸法を示しています。ドレインからソースに移動すると、反転層は次第に減少します。ここで、チャネル長Lの小さな領域dyを考慮すると、この領域によって提供される増分抵抗dRは次のように表すことができます。

$$dR=-\frac{dy}{w.\mu _{n}.Q1(y)}$$

ここで、マイナス符号は、反転層の電荷Q1とμの負極性によるもので_nは定数である表面移動度です。ここで、dR方程式のQ1（y）の値を代入します-

$$dR=-\frac{dy}{w.\mu _{n}.\left \{ -C_{ox}\left [ V_{GS}-V_{C\left ( Y \right )} \right ]-V_{TO} \right \}}$$

$$dR=\frac{dy}{w.\mu _{n}.C_{ox}\left [ V_{GS}-V_{C\left ( Y \right )} \right ]-V_{TO}}$$

これで、小さなdy領域での電圧降下は次の式で与えられます。

$$dV_{c}=I_{D}.dR$$

dRの値を上記の式に入れます

$$dV_{C}=I_{D}.\frac{dy}{w.\mu_{n}.C_{ox}\left [ V_{GS}-V_{C(Y)} \right ]-V_{TO}}$$

$$w.\mu _{n}.C_{ox}\left [ V_{GS}-V_{C(Y)}-V_{TO} \right ].dV_{C}=I_{D}.dy$$

チャネル領域全体のドレイン電流IDを取得するには、上記の式をチャネルに沿ってy = 0からy = Lおよび電圧VC _（y） = 0からVC _（y） = _VDSまで積分できます。

$$C_{ox}.w.\mu _{n}.\int_{V_{c}=0}^{V_{DS}} \left [ V_{GS}-V_{C\left ( Y \right )}-V_{TO} \right ].dV_{C} = \int_{Y=0}^{L}I_{D}.dy$$

$$\frac{C_{ox}.w.\mu _{n}}{2}\left ( 2\left [ V_{GS}-V_{TO} \right ] V_{DS}-V_{DS}^{2}\right ) = I_{D}\left [ L-0 \right ]$$

$$I_{D} = \frac{C_{ox}.\mu _{n}}{2}.\frac{w}{L}\left ( 2\left [ V_{GS}-V_{TO} \right ]V_{DS}-V_{DS}^{2} \right )$$

線形領域の場合_VDS <V _GS − _VTO。飽和領域の場合、V _DSの値は（V _GS − V _TO）よりも大きくなります。したがって、飽和領域の場合、V _DS =（V _GS − V _TO）。

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{\left [ 2V_{DS} \right ]V_{DS}-V_{DS}^{2}}{L} \right )$$

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{2V_{DS}^{2}-V_{DS}^{2}}{L} \right )$$

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{V_{DS}^{2}}{L} \right )$$

$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{\left [ V_{GS}-V_{TO} \right ]^{2}}{L} \right )$$

インバーターは本当にすべてのデジタル設計の中核です。その動作と特性が明確に理解されると、NANDゲート、加算器、乗算器、マイクロプロセッサなどのより複雑な構造の設計が大幅に簡素化されます。これらの複雑な回路の電気的動作は、インバーターで得られた結果を外挿することでほぼ完全に導き出すことができます。

インバーターの分析を拡張して、NAND、NOR、XORなどのより複雑なゲートの動作を説明できます。これらのゲートは、乗算器やプロセッサーなどのモジュールの構成要素を形成します。この章では、静的CMOSインバーター、つまりCMOSインバーターであるインバーターゲートの単一の化身に焦点を当てます。これは確かに現在最も人気があり、したがって私たちの特別な注意に値します。

動作原理

理想的なインバータの論理記号と真理値表を下図に示します。ここで、Aは入力であり、Bはノード電圧で表される反転出力です。Vにより正論理を使用して、論理1のブール値が示されている_ddは論理0が0 Vで表される_第Vインバータ閾値電圧であり、_DDのV / 2、_DDは出力電圧です。

出力はV 0から切り替えられ_ddは、入力がV未満である場合_番目。だから、0 <Vため_に<V_番目の出力は、論理0入力及びVに等しい_番目<V_で<Vの_DDはインバータのロジック1入力に等しいです。

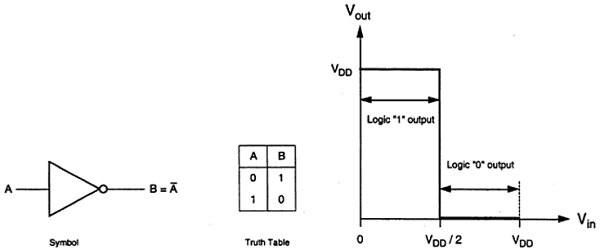
図に示す特性は理想的です。nMOSインバータの一般的な回路構造を下図に示します。

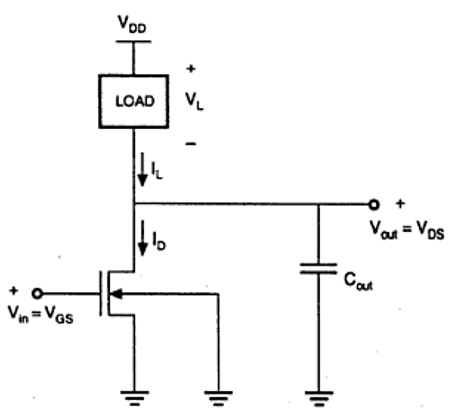
与えられた図から、インバータの入力電圧はnMOSトランジスタのゲート-ソース間電圧に等しく、インバータの出力電圧はnMOSトランジスタのドレイン-ソース間電圧に等しいことがわかります。nMOSのソース間電圧は、接地されたトランジスタのドライバとも呼ばれます。したがって、V _SS = 0です。出力ノードは、VTCに使用される集中容量に接続されています。

抵抗負荷インバータ

抵抗負荷インバータの基本構造を下図に示します。ここでは、エンハンスメント型nMOSがドライバトランジスタとして機能します。負荷は、単純な線形抵抗Rから成る_L。回路の電源はVである_DDとドレイン電流I _Dは、負荷電流Iに等しい_R。

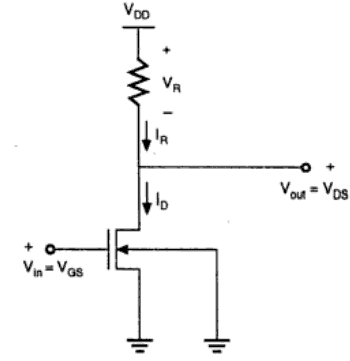
回路動作

ドライバトランジスタの入力がスレッショルド電圧_VTH（V _in <V _TH）未満の場合、ドライバトランジスタはカットオフ領域にあり、電流は流れません。したがって、負荷抵抗の両端の電圧降下はゼロであり、出力電圧は_VDDに等しくなります。ここで、入力電圧がさらに上昇すると、ドライバトランジスタがゼロ以外の電流を流し始め、nMOSが飽和領域に入ります。

数学的には、

$$I_{D} = \frac{K_{n}}{2}\left [ V_{GS}-V_{TO} \right ]^{2}$$

入力電圧をさらに上げると、ドライバトランジスタは線形領域に入り、ドライバトランジスタの出力は減少します。

$$I_{D} = \frac{K_{n}}{2}2\left [ V_{GS}-V_{TO} \right ]V_{DS}-V_{DS}^{2}$$

以下に示す抵抗負荷インバータのVTCは、ドライバトランジスタの動作モードと電圧ポイントを示します。

N型MOSFET負荷のインバータ

MOSFETを負荷デバイスとして使用する主な利点は、トランジスタが占めるシリコンの面積が、抵抗性負荷が占める面積よりも小さいことです。ここで、MOSFETはアクティブ負荷であり、アクティブ負荷のあるインバーターは、抵抗性負荷のあるインバーターよりも優れた性能を発揮します。

エンハンスメントロードNMOS

エンハンスメント型負荷装置を備えた2台のインバータを図に示します。負荷トランジスタは、ゲート端子に印加されるバイアス電圧に応じて、飽和領域または線形領域のいずれかで動作できます。飽和エンハンスメント負荷インバータを図1に示します。（a）。これは、単一の電圧源と、単純な製造工程を必要とし、Vよう_OH Vに制限されている_DD - V _T。

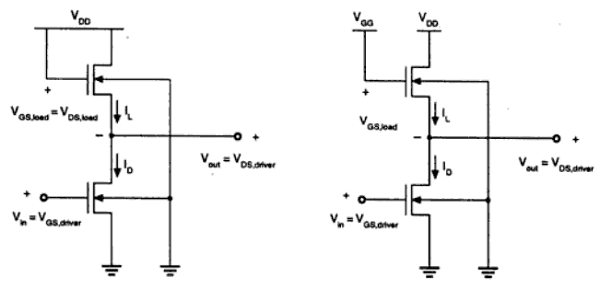
線形増強負荷インバータを図1に示します。（b）。常に線形領域で動作します。したがって、_VOHレベルは_VDDに等しくなります。

線形負荷インバーターは、飽和エンハンスメントインバーターと比較して高いノイズマージンを持っています。ただし、リニアエンハンスメントインバータの欠点は、2つの別々の電源が必要であり、両方の回路で高い電力損失が発生することです。したがって、エンハンスメントインバータは大規模なデジタルアプリケーションでは使用されません。

枯渇負荷NMOS

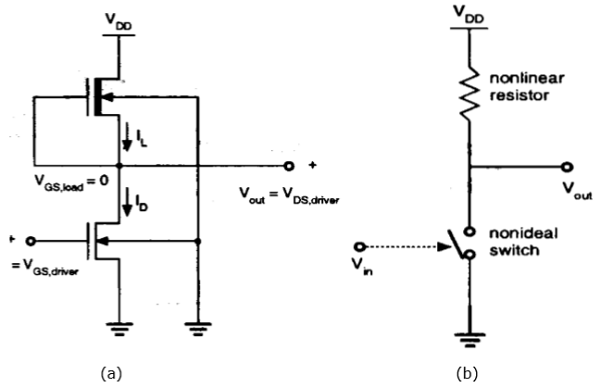
エンハンスメントロードインバーターの欠点は、デプレッションロードインバーターを使用することで克服できます。エンハンスメントロードインバーターと比較して、空乏ロードインバーターは、負荷のしきい値電圧を調整するためにチャネル注入のためのいくつかの製造ステップを必要とします。

枯渇負荷インバーターの利点は、シャープなVTC遷移、より優れたノイズマージン、単一電源、および全体的なレイアウト領域の縮小です。

図に示すように、負荷のゲート端子とソース端子が接続されています。したがって、V _GS = 0です。したがって、負荷のしきい値電圧は負です。したがって、

$$V_{GS,load}> V_{T,load}$$ 満足している

したがって、負荷デバイスには、入力および出力電圧レベルに関係なく、常に導通チャネルがあります。

負荷トランジスタが飽和領域にあるとき、負荷電流は次の式で与えられます。

$$I_{D,load} = \frac{K_{n,load}}{2}\left [ -V_{T,load}\left ( V_{out} \right ) \right ]^{2}$$

負荷トランジスタが線形領域にある場合、負荷電流は次の式で与えられます。

$$I_{D,load} = \frac{K_{n,load}}{2}\left [ 2\left | V_{T,load}\left ( V_{out} \right ) \right |.\left ( V_{DD}-V_{out} \right )-\left ( V_{DD}-V_{out} \right )^{2} \right ]$$

空乏負荷インバータの電圧伝達特性を下図に示します。

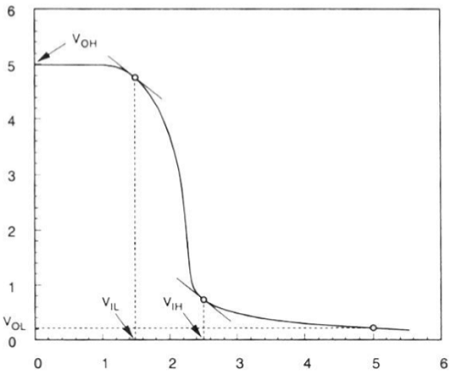
CMOSインバーター–回路、操作および説明

CMOSインバータ回路を図に示します。ここでは、nMOSおよびpMOSトランジスタがドライバトランジスタとして機能します。一方のトランジスタがオンのとき、もう一方はオフです。

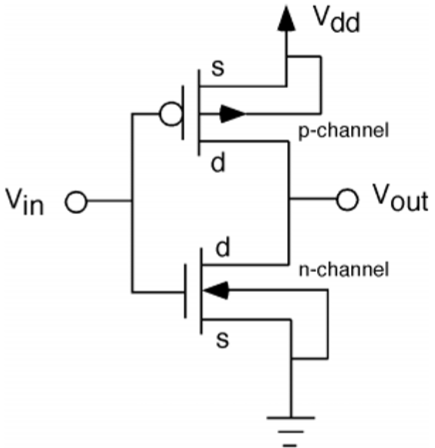
この構成はと呼ばれます complementary MOS (CMOS)。入力は両方のトランジスタのゲート端子に接続されているため、両方を入力電圧で直接駆動できます。nMOSトランジスタの基板は、グランドに接続され、pMOSの基板は電源、Vに接続されている_DD。

したがって、両方のトランジスタでV _SB = 0です。

$$V_{GS,n}=V_{in}$$

$$V_{DS,n}=V_{out}$$

そして、

$$V_{GS,p}=V_{in}-V_{DD}$$

$$V_{DS,p}=V_{out}-V_{DD}$$

nMOSの入力がスレッショルド電圧よりも小さい場合（V _in <V _TO、n）、nMOSはカットオフされ、pMOSは線形領域にあります。したがって、両方のトランジスタのドレイン電流はゼロです。

$$I_{D,n}=I_{D,p}=0$$

したがって、出力電圧_VOHは供給電圧に等しくなります。

$$V_{out}=V_{OH}=V_{DD}$$

入力電圧が_VDD + V _TO、pより大きい場合、pMOSトランジスタはカットオフ領域にあり、nMOSは線形領域にあるため、両方のトランジスタのドレイン電流はゼロです。

$$I_{D,n}=I_{D,p}=0$$

したがって、出力電圧_VOLはゼロに等しくなります。

$$V_{out}=V_{OL}=0$$

V _in > V _TOの場合、および以下の条件が満たされる場合、nMOSは飽和領域で動作します。

$$V_{DS,n}\geq V_{GS,n}-V_{TO,n} $$

$$V_{out}\geq V_{in}-V_{TO,n} $$

V _in <V _DD + V _TO、pの場合_、および以下の条件が満たされる場合_、 pMOSは飽和領域で動作します。

$$V_{DS,p}\leq V_{GS,p}-V_{TO,p} $$

$$V_{out}\leq V_{in}-V_{TO,p} $$

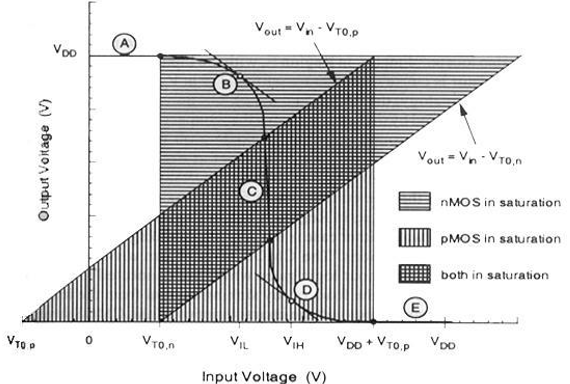
入力電圧の値が異なる場合、両方のトランジスタの動作領域を以下に示します。

領域	V in	Vアウト	nMOS	pMOS
A	<V TO、n	V OH	を中断する	線形
B	V IL	高≈V OH	飽和	線形
C	V番目	V番目	飽和	飽和
D	V IH	低≈V OL	線形	飽和
E	>（V DD + V TO、p）	V OL	線形	を中断する

CMOSのVTCを下図に示します-

複数の入力変数に対してブール演算を実行し、入力のブール関数として出力を決定する組み合わせ論理回路またはゲートは、すべてのデジタルシステムの基本的な構成要素です。2入力NANDゲートやNORゲートなどの単純な回路構成を調べてから、分析を複数入力回路構造のより一般的なケースに拡張します。

次に、CMOS論理回路を同様の方法で示します。nMOS空乏負荷論理回路とCMOS論理回路の類似点と相違点を強調し、例を挙げてCMOSゲートの利点を指摘します。最も一般的な形式では、ブール関数を実行する組み合わせ論理回路またはゲートは、図に示すように、複数入力、単一出力システムとして表すことができます。

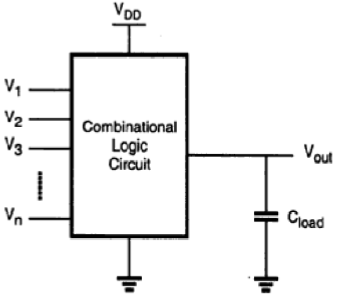
接地電位を基準としたノード電圧は、すべての入力変数を表します。正の論理規則を使用すると、「1」のブール（または論理）値はVDDの高電圧で表すことができ、「0」のブール（または論理）値は0の低電圧で表すことができます。ノードは、静電容量Cがロードさ_L回路における寄生素子の合成容量を表します。

CMOS論理回路

CMOS2入力NORゲート

この回路は、並列接続されたn-netと直列接続された相補型p-netで構成されています。入力電圧V _XおよびV _Yは、 1つのNMOS及び1つのPMOSトランジスタのゲートに印加されます。

一方または両方の入力がハイの場合、つまりn-netが出力ノードとグランドの間に導電パスを作成すると、p-netはカットオフされます。両方の入力電圧が低い場合、つまりn-netがカットオフされている場合、p-netは出力ノードと電源電圧の間に導通パスを作成します。

任意の入力の組み合わせに対して、相補回路構造は、出力が低抵抗パスを介してV _DDまたはグランドのいずれかに接続され、_VDDとグランド間のDC電流パスがどの入力の組み合わせに対しても確立されないようになっています。CMOSの出力電圧は、二つの入力NORゲートは、Vの論理ロー電圧取得する_OL = 0及びVの論理ハイ電圧_OH = V _DDを。切り換え閾値電圧Vの式_番目によって与えられます。

$$V_{th}\left ( NOR2 \right ) = \frac{V_{T,n}+\frac{1}{2}\sqrt{\frac{k_{p}}{k_{n}}\left ( V_{DD}-\left | V_{T,p} \right | \right )}}{1+\frac{1}{2}\sqrt{\frac{k_{p}}{k_{n}}}}$$

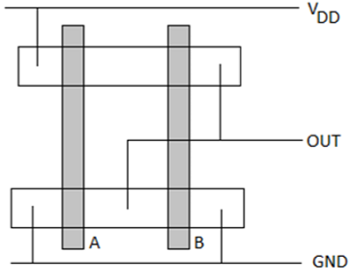
CMOS2入力NORゲートのレイアウト

この図は、単層金属と単層ポリシリコンを使用したCMOS2入力NORゲートのサンプルレイアウトを示しています。このレイアウトの特徴は次のとおりです。

• 入力ごとに単一の垂直ポリライン
• それぞれNデバイスとPデバイスの単一のアクティブな形状
• 水平に走る金属バス

CMOSN0R2ゲートのスティック図を次の図に示します。これはレイアウトに直接対応しますが、WおよびL情報は含まれていません。拡散領域は長方形で表され、金属接続と実線と円はそれぞれ接触を表し、網掛けの帯はポリシリコンカラムを表します。スティックダイアグラムは、最適なレイアウトトポロジを計画するのに役立ちます。

CMOS2入力NANDゲート

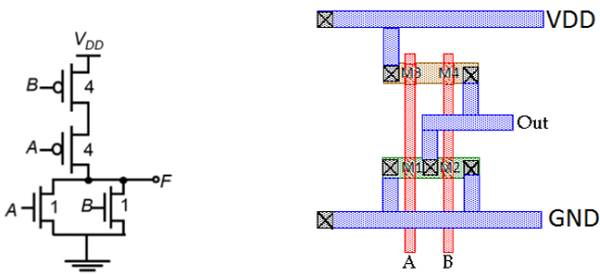
2入力CMOSNANDゲートの回路図を下図に示します。

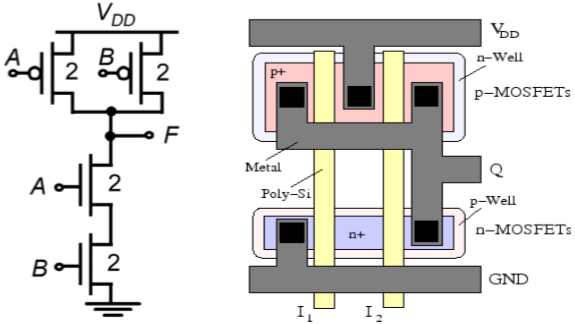
回路の動作原理は、CMOS2入力NOR動作の正確なデュアルです。2つの直列接続されたnMOSトランジスタで構成されるnネットは、両方の入力電圧が論理的に高い場合、出力ノードとグランドの間に導通パスを作成します。p-netで並列接続されたpMOSトランジスタは両方ともオフになります。

他のすべての入力の組み合わせでは、pMOSトランジスタの一方または両方がオンになり、p – netが遮断されるため、出力ノードと電源電圧の間に電流パスが作成されます。このゲートのスイッチングしきい値は、次のように取得されます。

$$V_{th}\left ( NAND2 \right ) = \frac{V_{T,n}+2\sqrt{\frac{k_{p}}{k_{n}}\left ( V_{DD}-\left | V_{T,p} \right | \right )}}{1+2\sqrt{\frac{k_{p}}{k_{n}}}}$$

このレイアウトの特徴は次のとおりです-

• 入力用の単一のポリシリコンラインは、NとPの両方のアクティブ領域を垂直に横切って走っています。
• 単一のアクティブシェイプは、両方のnMOSデバイスと両方のpMOSデバイスの構築に使用されます。
• パワーバスは、レイアウトの上部と下部で水平に実行されています。
• 隣接する回路に簡単に接続できるように、出力ワイヤは水平に配線されています。

複雑な論理回路

複雑な論理ゲートのNMOS枯渇負荷

複数の入力変数の複雑な機能を実現するために、NORおよびNAND用に開発された基本的な回路構造と設計原理を複雑な論理ゲートに拡張できます。少数のトランジスタを使用して複雑な論理機能を実現する機能は、nMOSおよびCMOS論理回路の最も魅力的な機能の1つです。例として、次のブール関数について考えてみます。

$$\overline{Z=P\left ( S+T \right )+QR}$$

この機能を実現するために使用されるnMOS空乏負荷複合論理ゲートを図に示します。この図では、3つのドライバトランジスタの左側のnMOSドライバブランチを使用して論理関数P（S + T）を実行し、右側のブランチを使用して関数QRを実行しています。2つの分岐を並列に接続し、負荷トランジスタを出力ノードと電源電圧の間に配置することによってV_DD,与えられた複素関数を取得します。各入力変数は、1つのドライバーにのみ割り当てられます。

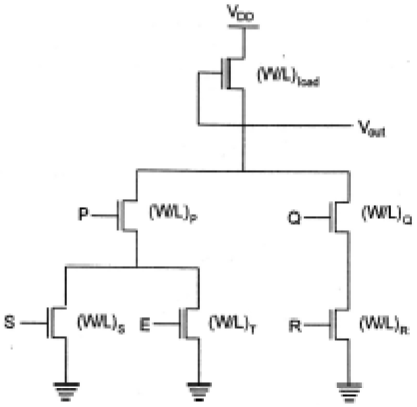
回路トポロジーを検査すると、プルダウンネットワークの簡単な設計原理が得られます。

• OR操作は、並列接続されたドライバーによって実行されます。
• AND演算は、直列接続されたドライバによって実行されます。
• 反転は、MOS回路動作の性質によって提供されます。

関数を実現する回路ですべての入力変数がロジックハイの場合、同等のドライバ (W/L) 5つのnMOSトランジスタで構成されるプルダウンネットワークの比率は次のとおりです。

$$\frac{W}{L}=\frac{1}{\frac{1}{\left ( W/L \right )Q}+\frac{1}{\left ( W/L \right )R}}+\frac{1}{\frac{1}{\left ( W/L \right )P}+\frac{1}{\left ( W/L \right )S+\left ( W/L \right )Q}}$$

複雑なCMOS論理ゲート

n-net、つまりプルダウンネットワークの実現は、nMOSの空乏負荷の複雑な論理ゲートについて検討したのと同じ基本的な設計原理に基づいています。pMOSプルアップネットワークは、n-netのデュアルネットワークである必要があります。

これは、nMOSネットワークのすべての並列接続がpMOSネットワークの直列接続に対応し、nMOSネットワークのすべての直列接続がpMOSネットワークの並列接続に対応することを意味します。この図は、n-net（プルダウン）グラフからのデュアルp-net（プルアップ）グラフの簡単な構成を示しています。

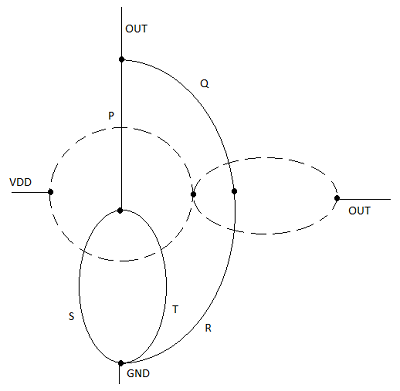
プルダウンネットワークの各ドライバトランジスタはaiで示され、各ノードはプルダウングラフの頂点で示されます。次に、プルダウングラフの各制限領域内に新しい頂点が作成され、隣接する頂点は、プルダウングラフの各エッジと1回だけ交差するエッジによって接続されます。この新しいグラフは、プルアップネットワークを示しています。

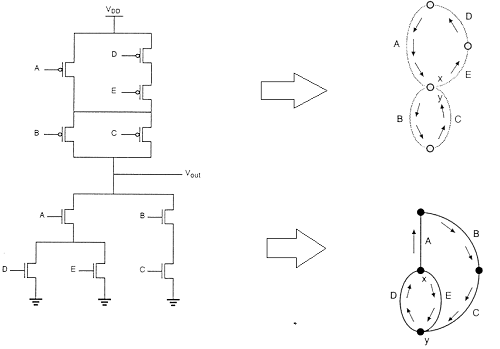
オイラーグラフ法を使用したレイアウト手法

この図は、複雑な関数のCMOS実装と、CMOSゲートのレイアウトが非常に最適でない任意のゲート順序で行われたスティック図を示しています。

この場合、ポリシリコンカラム間の分離により、その間の拡散から拡散への分離が可能になる必要があります。これは確かにかなりの量の余分なシリコン領域を消費します。

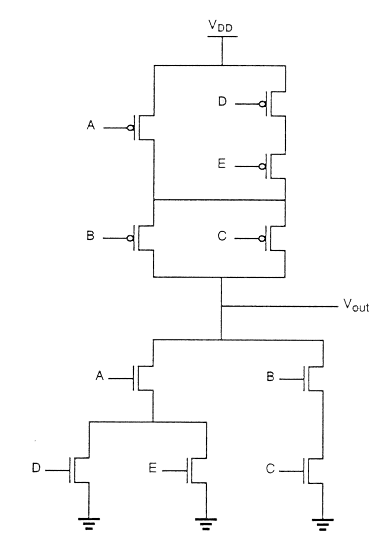
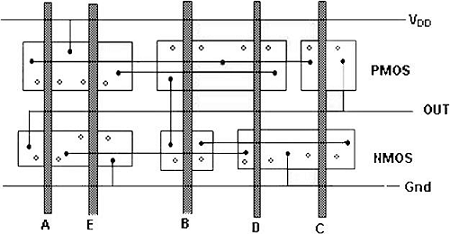
オイラーパスを使用することで、最適なレイアウトを得ることができます。オイラーパスは、グラフの各エッジ（ブランチ）を1回だけ横断する中断のないパスとして定義されます。入力の順序が同じであるプルダウンツリーグラフとプルアップツリーグラフの両方でオイラーパスを見つけます。

論理回路は、（a）組み合わせ回路と（b）順序回路の2つのカテゴリに分類されます。

組み合わせ回路では、出力は最新の入力の状​​態にのみ依存します。

シーケンシャル回路では、出力は最新の入力だけでなく、以前の入力の状​​態にも依存します。順序回路にはメモリ要素が含まれています。

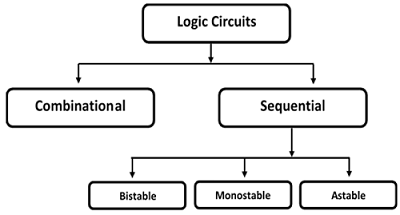
順序回路には3つのタイプがあります-

Bistable−双安定回路には2つの安定した動作点があり、どちらの状態にもなります。例-メモリセル、ラッチ、フリップフロップ、およびレジスタ。

Monostable−単安定回路には、安定した動作点が1つしかなく、一時的に反対の状態に摂動された場合でも、時間内に安定した動作点に戻ります。例：タイマー、パルスジェネレータ。

Astable−回路には安定した動作点がなく、いくつかの状態間で発振します。例-リングオシレータ。

CMOS論理回路

NORゲートに基づくSRラッチ

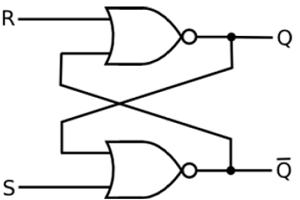
設定された入力（S）が論理に等しい場合 "1" リセット入力はロジックと同じです "0." 次に、出力Qは強制的にロジック化されます "1"。一方$\overline{Q}$ 論理に強制されます "0"。これは、以前の状態に関係なく、SRラッチが設定されることを意味します。

同様に、Sが「0」に等しく、Rがに等しい場合 "1" 次に、出力Qは強制されます "0" 一方 $\overline{Q}$ 強制されます "1"。これは、以前に保持されていた状態に関係なく、ラッチがリセットされることを意味します。最後に、入力SとRの両方がロジックに等しい場合"1" その後、両方の出力が強制的にロジック化されます "0" これはQとの相補性と矛盾します $\overline{Q}$。

したがって、この入力の組み合わせは、通常の操作では許可されていません。NORベースのSRラッチの真理値表を表に示します。

S	R	Q	$\overline{Q}$	操作
0	0	Q	$\overline{Q}$	ホールド
1	0	1	0	セットする
0	1	0	1	リセット
1	1	0	0	禁止されている

NORゲートに基づくCMOSSRラッチを下図に示します。

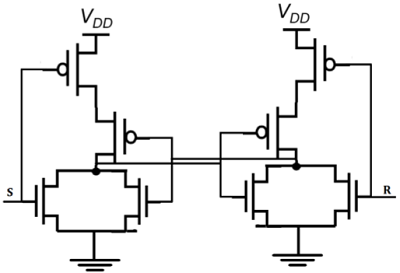
SはVに等しい場合_OH及びRはVに等しい_OL、M1とM2がオンになり、並列接続されたトランジスタの両方。ノードの電圧$\overline{Q}$V _OL = 0の論理ローレベルを想定します。

同時に、M3とM4の両方がどの論理ハイ電圧Vで結果、オフさ_OH RはVに等しい場合ノードQにおける_OH、SはVに等しい_OL、M1及びM2はオフとM3とM4がオンになっています。

NANDゲートに基づくSRラッチ

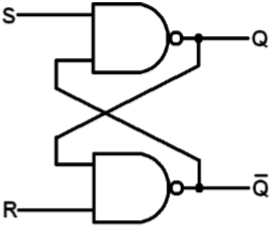
NANDベースのSRラッチのブロック図とゲートレベルの回路図を図に示します。SおよびR入力端子の小さな円は、回路がアクティブな低入力信号に応答することを表しています。NANDベースのSRラッチの真理値表を表に示します。

S	R	Q	Q '
0	0	NC	NC	変化なし。ラッチは現在の状態のままでした。
1	0	1	0	ラッチセット。
0	1	0	1	ラッチリセット。
1	1	0	0	条件が無効です。

Sが0になると（R = 1の場合）、Qがハイになり、プルします。 $\overline{Q}$ ローになり、ラッチはセット状態になります

S = 0 次にQ = 1 （R =の場合 1）

Rが0になると（S = 1の場合）、Qが高くなり、プルします。 $\overline{Q}$ ローで、ラッチはリセットされます

R = 0 次にQ = 1 （S =の場合 1）

ホールド状態では、SとRの両方がハイである必要があります。S = R = 0の場合、状態が不確定になるため、出力は許可されません。NANDゲートに基づくCMOSSRラッチを図に示します。

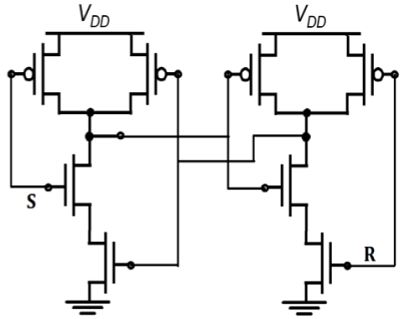
NANDゲートに基づく空乏負荷nMOSSRラッチを図に示します。操作は、CMOS NANDSRラッチの操作と同様です。CMOS回路の実装は、静的消費電力が低く、ノイズマージンが高くなっています。

CMOS論理回路

クロックドSRラッチ

この図は、クロックが追加されたNORベースのSRラッチを示しています。ラッチは、CLKがハイの場合にのみ入力SとRに応答します。

CLKがローの場合、ラッチは現在の状態を保持します。Qが状態を変化させることを観察します-

• 正のCLK中にSがハイになったとき。
• CLKロー時間中にS＆Rが変化した後のCLKの先行エッジ。
• CLKがハイのときのSの正のグリッチ
• 正のCLK中にRがハイになったとき。

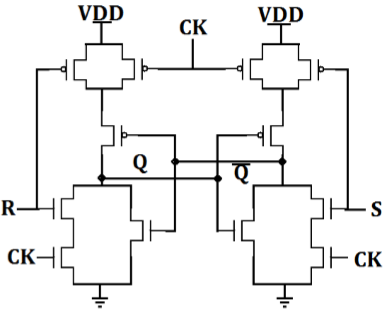
クロックドNORベースのSRラッチのCMOSAOI実装を図に示します。必要なトランジスタは12個だけであることに注意してください。

• CLKがローの場合、NツリーNの2つの直列端子が開いており、ツリーPの2つの並列トランジスタがオンになっているため、メモリセルの状態が保持されます。

• クロックがハイの場合、回路は入力SとRに応答するNORベースのCMOSラッチになります。

Clocked SR Latch based on NAND Gate

回路は4つのNANDゲートで実装されています。この回路がCMOSで実装されている場合、16個のトランジスタが必要です。

• ラッチは、CLKがハイの場合にのみSまたはRに応答します。
• 入力信号とCLK信号の両方がアクティブハイの場合、つまり、CLK = "1" S = "1"およびR = "0"の場合、ラッチ出力Qが設定されます。
• 同様に、CLK = "1"、S = "0"の場合、ラッチはリセットされます。

CLKがローの場合、ラッチは現在の状態を保持します。

クロックドJKラッチ

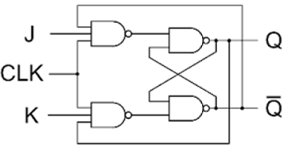
上の図は、NANDゲートに基づくクロック付きJKラッチを示しています。SRラッチの欠点は、SとRの両方がハイの場合、その出力状態が不確定になることです。JKラッチは、出力から入力へのフィードバックを使用してこの問題を排除し、真理値表のすべての入力状態が許容されるようにします。J = K = 0の場合、ラッチは現在の状態を保持します。

J = 1およびK = 0の場合、ラッチは次の正方向のクロックエッジ、つまりQ = 1に設定されます。 $\overline{Q}$ = 0

J = 0およびK = 1の場合、ラッチは次の正方向のクロックエッジ、つまりQ = 1および $\overline{Q}$ = 0。

J = K = 1の場合、ラッチは次の正方向のクロックエッジでトグルします

クロックドJKラッチの動作は、表に示されている真理値表に要約されています。

J	K	Q	$\overline{Q}$	S	R	Q	$\overline{Q}$	Operation
0	0	0	1	1	1	0	1	ホールド
		1	0	1	1	1	0
0	1	0	1	1	1	0	1	リセット
		1	0	1	0	0	1
1	0	0	1	0	1	1	0	セットする
		1	0	1	1	1	0
1	1	0	1	0	1	1	0	トグル
		1	0	1	0	0	1

CMOSDラッチの実装

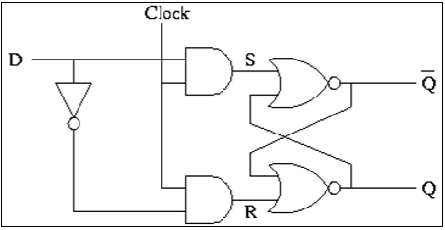
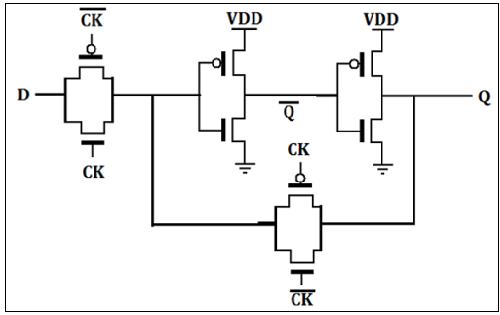
Dラッチは通常、図に示すようにトランスミッションゲート（TG）スイッチで実装されます。入力TGはCLKでアクティブになり、ラッチフィードバックループTGはCLKでアクティブになります。入力Dは、CLKがハイのときに受け入れられます。CLKがローになると、入力が開回路になり、ラッチは前のデータDで設定されます。

VHDLは、非常に高速な集積回路ハードウェア記述言語の略です。これは、データフロー、動作および構造スタイルのモデリングによってデジタルシステムをモデル化するために使用されるプログラミング言語です。この言語は、1981年にVHSICプログラムの下で国防総省（DoD）に最初に導入されました。

デザインの説明

VHDLでは、エンティティはハードウェアモジュールを記述するために使用されます。エンティティは、を使用して記述できます。

• エンティティ宣言
• Architecture
• Configuration
• パッケージ宣言
• パッケージ本体

これらは何ですか？

エンティティ宣言

ハードウェアモジュールの名前、入出力信号、およびモードを定義します。

Syntax −

entity entity_name is
   Port declaration;
end entity_name;

エンティティ宣言は、「entity」で始まり、「end」キーワードで終わる必要があります。方向は、入力、出力、または入力になります。

に	ポートを読み取ることができます
アウト	ポートを書き込むことができます
アウト	ポートは読み取りと書き込みが可能
バッファ	ポートは読み取りと書き込みが可能で、ソースは1つだけです。

Architecture −

アーキテクチャは、構造、データフロー、動作、または混合スタイルを使用して記述できます。

Syntax −

architecture architecture_name of entity_name 
architecture_declarative_part;

begin
   Statements;
end architecture_name;

ここでは、アーキテクチャ本体を作成するエンティティ名を指定する必要があります。アーキテクチャステートメントは、「begin」および「énd」キーワード内にある必要があります。アーキテクチャ宣言部分には、変数、定数、またはコンポーネント宣言が含まれる場合があります。

データフローモデリング

このモデリングスタイルでは、エンティティを通過するデータの流れは、同時（並列）信号を使用して表現されます。VHDLの並行ステートメントは、WHENとGENERATEです。

それらに加えて、演算子（AND、NOT、+、*、sllなど）のみを使用した割り当てを使用してコードを作成することもできます。

最後に、BLOCKと呼ばれる特別な種類の割り当ても、この種類のコードで使用できます。

並行コードでは、以下を使用できます-

• Operators
• WHENステートメント（WHEN / ELSEまたはWITH / SELECT / WHEN）;
• GENERATEステートメント;
• BLOCKステートメント

行動モデリング

このモデリングスタイルでは、ステートメントのセットとしてのエンティティの動作は、指定された順序で順番に実行されます。PROCESS、FUNCTION、またはPROCEDURE内に配置されたステートメントのみが順次です。

PROCESSES、FUNCTIONS、およびPROCEDURESは、順次実行されるコードの唯一のセクションです。

ただし、全体として、これらのブロックはいずれも、その外部に配置された他のステートメントと同時に実行されます。

ビヘイビアコードの重要な側面の1つは、シーケンシャルロジックに限定されないことです。実際、これを使用すると、組み合わせ回路だけでなく順序回路も構築できます。

動作ステートメントは、IF、WAIT、CASE、およびLOOPです。VARIABLESも制限されており、シーケンシャルコードでのみ使用されることになっています。VARIABLEをグローバルにすることはできないため、その値を直接渡すことはできません。

構造モデリング

このモデリングでは、エンティティは相互接続されたコンポーネントのセットとして記述されます。コンポーネントのインスタンス化ステートメントは、並行ステートメントです。したがって、これらのステートメントの順序は重要ではありません。モデリングの構造スタイルは、コンポーネント自体の動作やコンポーネントが集合的に表すエンティティの動作を意味することなく、コンポーネントの相互接続（ブラックボックスとして表示）のみを記述します。

構造モデリングでは、アーキテクチャ本体は2つの部分で構成されます。宣言部分（キーワードbeginの前）とステートメント部分（キーワードbeginの後）です。

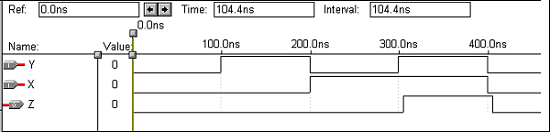
論理演算– AND GATE

バツ	Y	Z
0	0	0
0	1	0
1	0	0
1	1	1

VHDL Code:
Library ieee;
use ieee.std_logic_1164.all;

entity and1 is
   port(x,y:in bit ; z:out bit);
end and1;

architecture virat of and1 is
begin
   z<=x and y; 
end virat;

波形

論理演算–ORゲート

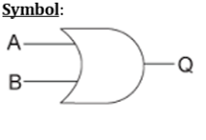
バツ	Y	Z
0	0	0
0	1	1
1	0	1
1	1	1

VHDL Code: 
Library ieee; 
use ieee.std_logic_1164.all;  

entity or1 is
   port(x,y:in bit ; z:out bit); 
end or1; 
 
architecture virat of or1 is
begin
   z<=x or y; 
end virat;

波形

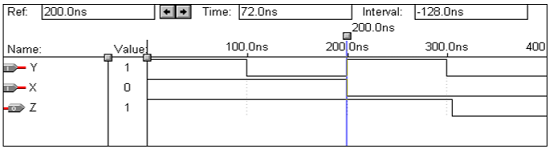
論理演算–ゲートではありません

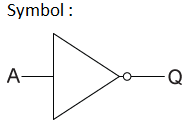
バツ	Y
0	1
1	0

VHDL Code:
  
Library ieee; 
use ieee.std_logic_1164.all; 
 
entity not1 is
   port(x:in bit ; y:out bit); 
end not1; 
 
architecture virat of not1 is
begin
   y<=not x;
end virat;

波形

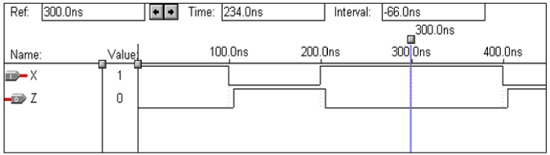
論理演算–NANDゲート

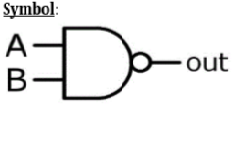
バツ	Y	z
0	0	1
0	1	1
1	0	1
1	1	0

VHDL Code:
  
Library ieee; 
use ieee.std_logic_1164.all; 

entity nand1 is
   port(a,b:in bit ; c:out bit); 
end nand1; 
 
architecture virat of nand1 is
begin
   c<=a nand b; 
end virat;

波形

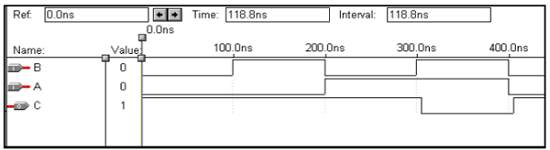
論理演算–NORゲート

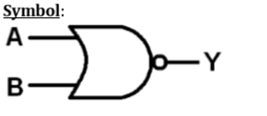
バツ	Y	z
0	0	1
0	1	0
1	0	0
1	1	0

VHDL Code: 
 
Library ieee; 
use ieee.std_logic_1164.all; 
 
entity nor1 is
   port(a,b:in bit ; c:out bit); 
end nor1; 
 
architecture virat of nor1 is
begin
   c<=a nor b;
end virat;

波形

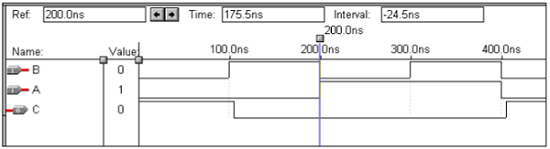
論理演算–XORゲート

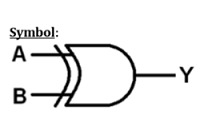
バツ	Y	Z
0	0	1
0	1	1
1	0	1
1	1	0

VHDL Code: 
 
Library ieee; 
use ieee.std_logic_1164.all;
  
entity xor1 is
   port(a,b:in bit ; c:out bit); 
end xor1;
  
architecture virat of xor1 is
begin
   c<=a xor b; 
end virat;

波形

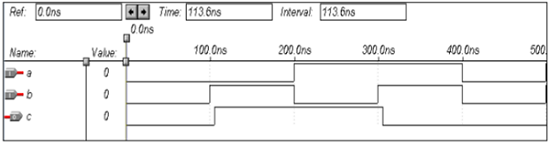
論理演算–X-NORゲート

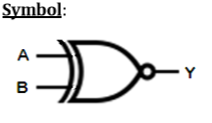
バツ	Y	Z
0	0	1
0	1	1
1	0	1
1	1	0

VHDL Code: 
 
Library ieee; 
use ieee.std_logic_1164.all; 

entity xnor1 is
   port(a,b:in bit ; c:out bit); 
end xnor1; 
 
architecture virat of xnor1 is
begin
   c<=not(a xor b); 
end virat;

波形

この章では、組み合わせ回路のVHDLプログラミングについて説明します。

半加算器のVHDLコード

VHDL Code:
  
Library ieee; 
use ieee.std_logic_1164.all;
  
entity half_adder is
   port(a,b:in bit; sum,carry:out bit); 
end half_adder; 
 
architecture data of half_adder is
begin
   sum<= a xor b;  
   carry <= a and b;  
end data;

波形

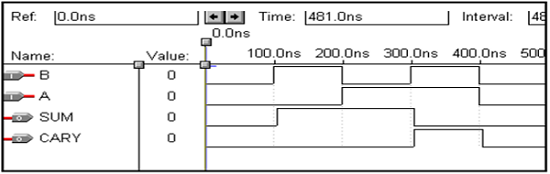
全加算器のVHDLコード

Library ieee; 
use ieee.std_logic_1164.all;
 
entity full_adder is port(a,b,c:in bit; sum,carry:out bit); 
end full_adder;
  
architecture data of full_adder is
begin
   sum<= a xor b xor c; 
   carry <= ((a and b) or (b and c) or (a and c)); 
end data;

波形

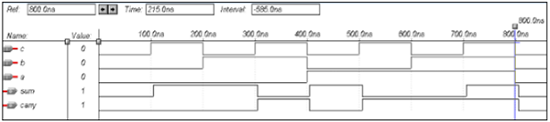
ハーフ減算器のVHDLコード

Library ieee;
use ieee.std_logic_1164.all;
  
entity half_sub is
   port(a,c:in bit; d,b:out bit);
end half_sub;  

architecture data of half_sub is
begin
   d<= a xor c;
   b<= (a and (not c));
end data;

波形

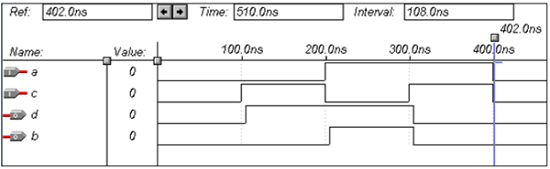
フル減算器のVHDLコード

Library ieee; 
use ieee.std_logic_1164.all;
  
entity full_sub is
   port(a,b,c:in bit; sub,borrow:out bit); 
end full_sub; 
 
architecture data of full_sub is
begin
   sub<= a xor b xor c; 
   borrow <= ((b xor c) and (not a)) or (b and c); 
end data;

波形

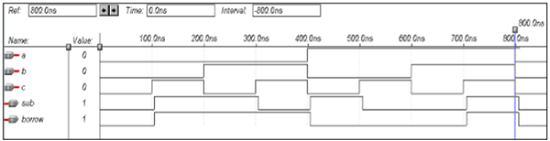
マルチプレクサのVHDLコード

Library ieee; 
use ieee.std_logic_1164.all;
  
entity mux is
   port(S1,S0,D0,D1,D2,D3:in bit; Y:out bit);
end mux;
  
architecture data of mux is
begin 
   Y<= (not S0 and not S1 and D0) or 
      (S0 and not S1 and D1) or 
      (not S0 and S1 and D2) or
      (S0 and S1 and D3); 
end data;

波形

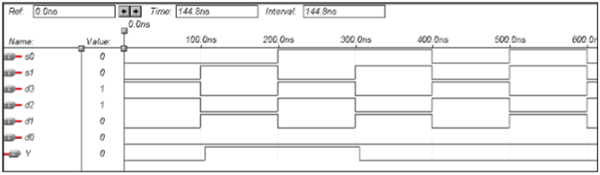
デマルチプレクサ用のVHDLコード

Library ieee; 
use ieee.std_logic_1164.all;
  
entity demux is
   port(S1,S0,D:in bit; Y0,Y1,Y2,Y3:out bit); 
end demux;
  
architecture data of demux is
begin 
   Y0<=  ((Not S0) and (Not S1) and D); 
   Y1<=  ((Not S0) and S1 and D); 
   Y2<=  (S0 and (Not S1) and D); 
   Y3<=  (S0 and S1 and D); 
end data;

波形

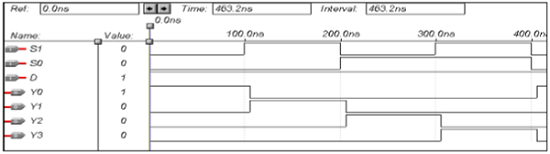
8 x3エンコーダーのVHDLコード

library ieee; 
use ieee.std_logic_1164.all; 
 
entity enc is
   port(i0,i1,i2,i3,i4,i5,i6,i7:in bit; o0,o1,o2: out bit); 
end enc; 
 
architecture vcgandhi of enc is
begin 
   o0<=i4 or i5 or i6 or i7; 
   o1<=i2 or i3 or i6 or i7; 
   o2<=i1 or i3 or i5 or i7; 
end vcgandhi;

波形

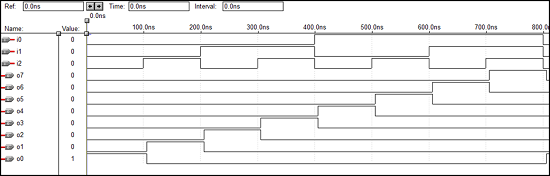
3 x8デコーダーのVHDLコード

library ieee; 
use ieee.std_logic_1164.all;

entity dec is
   port(i0,i1,i2:in bit; o0,o1,o2,o3,o4,o5,o6,o7: out bit); 
end dec; 
 
architecture vcgandhi of dec is
begin 
   o0<=(not i0) and (not i1) and (not i2); 
   o1<=(not i0) and (not i1) and i2; 
   o2<=(not i0) and i1 and (not i2); 
   o3<=(not i0) and i1 and i2; 
   o4<=i0 and (not i1) and (not i2); 
   o5<=i0 and (not i1) and i2; 
   o6<=i0 and i1 and (not i2); 
   o7<=i0 and i1 and i2; 
end vcgandhi;

波形

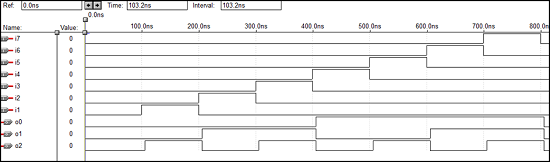
VHDLコード–4ビット並列加算器

library IEEE; 
use IEEE.STD_LOGIC_1164.all;
  
entity pa is
   port(a : in STD_LOGIC_VECTOR(3 downto 0);
      b : in STD_LOGIC_VECTOR(3 downto 0);
      ca : out STD_LOGIC;
      sum : out STD_LOGIC_VECTOR(3 downto 0) 
   ); 
end pa; 
 
architecture vcgandhi of pa is
   Component fa is
      port (a : in STD_LOGIC; 
         b : in STD_LOGIC; 
         c : in STD_LOGIC; 
         sum : out STD_LOGIC; 
         ca : out STD_LOGIC
      ); 
   end component;         
   signal s : std_logic_vector (2 downto 0); 
   signal temp: std_logic;
begin 
   temp<='0'; 
   u0 : fa port map (a(0),b(0),temp,sum(0),s(0)); 
   u1 : fa port map (a(1),b(1),s(0),sum(1),s(1)); 
   u2 : fa port map (a(2),b(2),s(1),sum(2),s(2));
   ue : fa port map (a(3),b(3),s(2),sum(3),ca);  
end vcgandhi;

波形

VHDLコード–4ビットパリティチェッカー

library ieee; 
use ieee.std_logic_1164.all; 
 
entity parity_checker is 
   port (a0,a1,a2,a3 : in std_logic; 
      p : out std_logic); 
end parity_checker;  

architecture vcgandhi of parity_checker is 
begin    
   p <= (((a0 xor a1) xor a2) xor a3); 
end vcgandhi;

波形

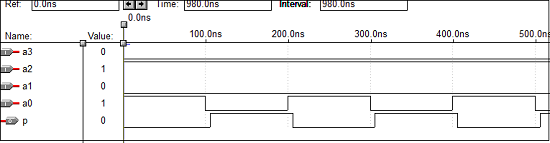
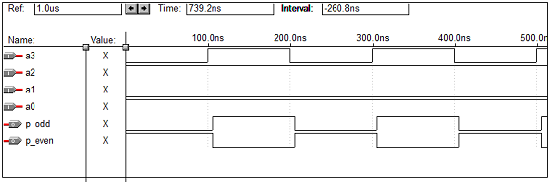
VHDLコード–4ビットパリティジェネレータ

library ieee;
use ieee.std_logic_1164.all;

entity paritygen is
   port (a0, a1, a2, a3: in std_logic; p_odd, p_even: out std_logic);
end paritygen;  

architecture vcgandhi of paritygen is
begin
   process (a0, a1, a2, a3)
   
	if (a0 ='0' and a1 ='0' and a2 ='0' and a3 =’0’)
      then odd_out <= "0";
      even_out <= "0";
   else
      p_odd <= (((a0 xor a1) xor a2) xor a3);
      p_even <= not(((a0 xor a1) xor a2) xor a3);  
end vcgandhi

波形

この章では、シーケンシャル回路のVHDLプログラミングを行う方法について説明します。

SRラッチのVHDLコード

library ieee; 
use ieee.std_logic_1164.all;
  
entity srl is 
   port(r,s:in bit; q,qbar:buffer bit); 
end srl;  

architecture virat of srl is 
   signal s1,r1:bit; 
begin 
   q<= s nand qbar; 
   qbar<= r nand q; 
end virat;

波形

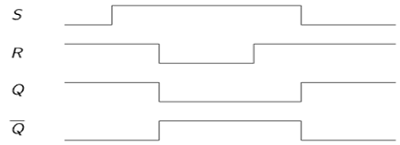
DラッチのVHDLコード

library ieee; 
use ieee.std_logic_1164.all;

entity Dl is 
   port(d:in bit; q,qbar:buffer bit); 
end Dl; 
 
architecture virat of Dl is 
   signal s1,r1:bit; 
begin 
   q<= d nand qbar; 
   qbar<= d nand q; 
end virat;

波形

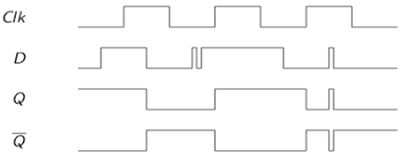
SRフリップフロップのVHDLコード

library ieee; 
use ieee.std_logic_1164.all;
  
entity srflip is 
   port(r,s,clk:in bit; q,qbar:buffer bit); 
end srflip;
  
architecture virat of srflip is 
   signal s1,r1:bit; 
begin 
   s1<=s nand clk; 
   r1<=r nand clk;
   q<= s1 nand qbar;
   qbar<= r1 nand q;
end virat;

波形

JKフリップフロップのVHDLコード

library IEEE; 
use IEEE.STD_LOGIC_1164.all;  

entity jk is 
   port(
      j : in STD_LOGIC; 
      k : in STD_LOGIC; 
      clk : in STD_LOGIC; 
      reset : in STD_LOGIC; 
      q : out STD_LOGIC; 
      qb : out STD_LOGIC 
   ); 
end jk;
  
architecture virat of jk is 
begin 
   jkff : process (j,k,clk,reset) is 
   variable m : std_logic := '0'; 
   
   begin 
      if (reset = '1') then 
         m : = '0'; 
      elsif (rising_edge (clk)) then 
         if (j/ = k) then
            m : = j; 
         elsif (j = '1' and k = '1') then 
            m : = not m; 
         end if; 
      end if; 
      
      q <= m; 
      qb <= not m; 
   end process jkff; 
end virat;

波形

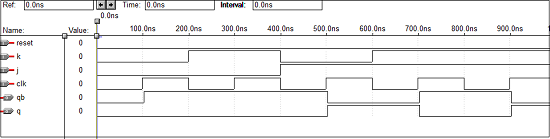
DフリップフロップのVHDLコード

Library ieee; 
use ieee.std_logic_1164.all;  

entity dflip is 
   port(d,clk:in bit; q,qbar:buffer bit); 
end dflip; 
 
architecture virat of dflip is 
   signal d1,d2:bit; 
begin 
   d1<=d nand clk; 
   d2<=(not d) nand clk; 
   q<= d1 nand qbar; 
   qbar<= d2 nand q; 
end virat;

波形

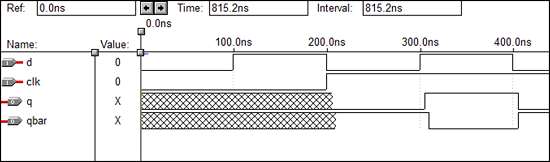
TフリップフロップのVHDLコード

library IEEE; 
use IEEE.STD_LOGIC_1164.all;  

entity Toggle_flip_flop is 
   port( 
      t : in STD_LOGIC; 
      clk : in STD_LOGIC; 
      reset : in STD_LOGIC; 
      dout : out STD_LOGIC
   ); 
end Toggle_flip_flop;  

architecture virat of Toggle_flip_flop is 
begin 
   tff : process (t,clk,reset) is 
   variable m : std_logic : = '0'; 
   
   begin 
      if (reset = '1') then 
         m : = '0'; 
      elsif (rising_edge (clk)) then 
         if (t = '1') then 
            m : = not m;        
         end if; 
      end if; 
      dout < = m; 
   end process tff; 
end virat;

波形

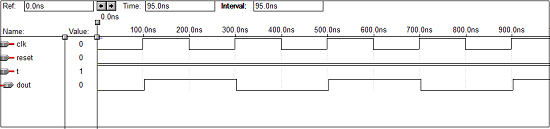
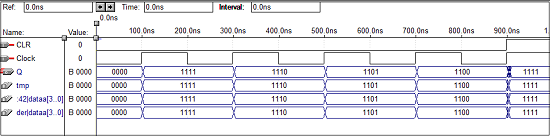
4ビットアップカウンターのVHDLコード

library IEEE; 
use ieee.std_logic_1164.all; 
use ieee.std_logic_unsigned.all;
  
entity counter is 
   port(Clock, CLR : in std_logic; 
      Q : out std_logic_vector(3 downto 0)
   ); 
end counter;  

architecture virat of counter is 
   signal tmp: std_logic_vector(3 downto 0); 
begin 
   process (Clock, CLR) 
   
   begin 
      if (CLR = '1') then 
         tmp < = "0000"; 
      elsif (Clock'event and Clock = '1') then 
         mp <= tmp + 1; 
      end if; 
   end process; 
   Q <= tmp; 
end virat;

波形

4ビットダウンカウンターのVHDLコード

library ieee; 
use ieee.std_logic_1164.all; 
use ieee.std_logic_unsigned.all;
  
entity dcounter is 
   port(Clock, CLR : in std_logic; 
      Q : out std_logic_vector(3 downto 0)); 
end dcounter; 
 
architecture virat of dcounter is 
   signal tmp: std_logic_vector(3 downto 0); 

begin 
   process (Clock, CLR) 
   begin 
      if (CLR = '1') then 
         tmp <= "1111"; 
      elsif (Clock'event and Clock = '1') then 
         tmp <= tmp - 1; 
      end if; 
   end process; 
   Q <= tmp; 
end virat;

波形

Verilogはハードウェア記述言語（HDL）です。これは、ネットワークスイッチ、マイクロプロセッサ、メモリ、フリップフロップなどのデジタルシステムを記述するために使用される言語です。つまり、HDLを使用することで、あらゆるレベルのあらゆるデジタルハードウェアを記述できます。HDLで記述されている設計は、テクノロジに依存せず、設計とデバッグが非常に簡単であり、通常、特に大規模な回路の場合、回路図よりも便利です。

Verilogは、さまざまな抽象化レベルで設計をサポートします。主要な3つは-

• 行動レベル
• レジスタ転送レベル
• ゲートレベル

行動レベル

このレベルは、並行アルゴリズム（動作）によってシステムを記述します。すべてのアルゴリズムはシーケンシャルです。つまり、1つずつ実行される一連の命令で構成されます。関数、タスク、およびブロックが主要な要素です。デザインの構造的な実現には関係ありません。

レジスタ転送レベル

レジスタ転送レベルを使用する設計では、演算とレジスタ間のデータ転送を使用して回路の特性を指定します。RTLコードの最新の定義は、「合成可能なコードはすべてRTLコードと呼ばれます」です。

ゲートレベル

論理レベル内では、システムの特性は論理リンクとそのタイミングプロパティによって記述されます。すべての信号は離散信号です。それらは明確な論理値（ `0 '、` 1'、 `X '、` Z`）のみを持つことができます。使用可能な操作は、事前定義された論理プリミティブ（基本ゲート）です。ゲートレベルのモデリングは、ロジック設計にとって正しいアイデアではない場合があります。ゲートレベルのコードは、合成ツールなどのツールを使用して生成され、彼のネットリストはゲートレベルのシミュレーションとバックエンドに使用されます。

字句トークン

Verilog言語のソーステキストファイルは、字句トークンのストリームです。トークンは1つ以上の文字で構成され、各1文字は正確に1つのトークンに含まれます。

Verilog HDLで使用される基本的な字句トークンは、Cプログラミング言語のものと似ています。Verilogでは大文字と小文字が区別されます。すべてのキーワードは小文字です。

ホワイトスペース

空白には、スペース、タブ、新行、およびフォームフィードの文字を含めることができます。これらの文字は、トークンを区切る場合を除いて無視されます。

空白文字は、空白、タブ、キャリッジリターン、改行、およびフォームフィードです。

コメント

コメントを表す2つの形式があります

• 1）1行のコメントは、トークン//で始まり、キャリッジリターンで終わります。

例：//これは1行の構文です

• 2）複数行コメントはトークン/ *で始まり、トークン* /で終わります。

例：/ *これは複数行の構文です* /

数字

数値は、2進数、8進数、10進数、または16進数の形式で指定できます。負の数は2の補数で表されます。Verilogでは、整数、実数、符号付きおよび符号なしの数値を使用できます。

構文は次の式で与えられます-<サイズ> <基数> <値>

サイズまたはサイズなしの数値は<Size>で定義でき、<radix>は、2進数、8進数、16進数、または10進数のいずれであるかを定義します。

識別子

識別子は、関数、モジュール、レジスタなどのオブジェクトを定義するために使用される名前です。識別子は、アルファベット文字またはアンダースコア文字で始める必要があります。例 A_Z、a_z、_

識別子は、アルファベット、数字、アンダースコア、および$文字の組み合わせです。最大1024文字の長さにすることができます。

演算子

演算子は、条件を設定したり、変数を操作したりするために使用される特殊文字です。変数の操作を実行するために使用される文字は1つ、2つ、場合によっては3つあります。

例 >、+、〜、＆！=。

Verilogキーワード

Verilogで特別な意味を持つ単語は、Verilogキーワードと呼ばれます。たとえば、assign、case、while、wire、reg、and、or、nand、moduleなどです。それらは識別子として使用されるべきではありません。Verilogキーワードには、コンパイラ指令、システムタスクおよび関数も含まれます。

ゲートレベルモデリング

Verilogには、論理ゲート、伝送ゲート、スイッチなどのプリミティブが組み込まれています。これらは設計作業に使用されることはめったにありませんが、ASIC / FPGAセルのモデリングのために合成後の世界で使用されます。

ゲートレベルモデリングは2つの特性を示します-

Drive strength−出力ゲートの強度はドライブ強度によって定義されます。ソースに直接接続している場合、出力が最も強くなります。接続が導電性トランジスタを介している場合、およびプルアップ/ダウン抵抗を介して接続されている場合、強度は低下します。通常、ドライブ強度は指定されていません。この場合、強度はデフォルトでstrong1とstrong0になります。

Delays−遅延が指定されていない場合、ゲートには伝搬遅延がありません。2つの遅延が指定されている場合、最初の遅延は立ち上がり遅延を表し、2番目の遅延は立ち下がり遅延を表します。遅延が1つだけ指定されている場合、立ち上がりと立ち下がりの両方が等しくなります。合成では遅延は無視できます。

ゲートプリミティブ

Verilogでは、1つの出力と多くの入力を使用する基本的な論理ゲートが使用されます。GATEは、キーワードの1つを使用します-and、nand、or、nor、xor、xnorは、VerilogでN個の入力と1個の出力に使用されます。

Example:  
   Module gate() 
   Wire ot0; 
   Wire ot1; 
   Wire ot2; 
   
   Reg in0,in1,in2,in3; 
   Not U1(ot0,in0); 
   Xor U2(ot1,in1,in2,in3); 
   And U3(ot2, in2,in3,in0)

トランスミッションゲートプリミティブ

トランスミッションゲートプリミティブには、バッファとインバータの両方が含まれます。それらには、単一の入力と1つ以上の出力があります。以下に示すゲートインスタンス化構文では、GATEはキーワードbufまたはNOTゲートのいずれかを表します。

例：Not、buf、bufif0、bufif1、notif0、notif1

ない– noutoutインバーター

Buf –n出力バッファー

Bufifo –トライステートバッファ、アクティブローイネーブル

Bufif1 –トライステートバッファ、アクティブハイイネーブル

Notifo –トライステートインバーター、アクティブローイネーブル

Notif1 –トライステートインバーター、アクティブハイイネーブル

Example:  
   Module gate() 
   Wire out0; 
   Wire out1; 
   
   Reg in0,in1;
   Not U1(out0,in0); 
   Buf U2(out0,in0);

データ型

値セット

Verilogは、主に4つの基本値で構成されます。Verilogで使用されるすべてのVerilogデータ型は、これらの値を格納します-

0（論理ゼロ、または誤った条件）

1（論理的なもの、または真の状態）

x（不明な論理値）

z（高インピーダンス状態）

xとzの使用は、合成には非常に制限されています。

ワイヤー

ワイヤは、回路内の物理的なワイヤを表すために使用され、ゲートまたはモジュールの接続に使用されます。ワイヤの値は読み取りのみが可能で、関数またはブロックに割り当てることはできません。ワイヤは値を格納できませんが、常に連続割り当てステートメントによって、またはワイヤをゲート/モジュールの出力に接続することによって駆動されます。他の特定の種類のワイヤーは次のとおりです。

Wand (wired-AND) −ここで、Wandの値は、それに接続されているすべてのデバイスドライバーの論理ANDに依存します。

Wor (wired-OR) −ここで、Worの値は、それに接続されているすべてのデバイスドライバーの論理ORに依存します。

Tri (three-state) −ここで、triに接続されているすべてのドライバーはzでなければなりません。ただし、1つだけ（triの値を決定する）を除きます。

Example: 
   Wire [msb:lsb] wire_variable_list; 
   Wirec // simple wire 
   Wand d; 
   
   Assign d = a; // value of d is the logical AND of 
   Assign d = b; // a and b 
   Wire [9:0] A; // a cable (vector) of 10 wires. 
   
   Wand [msb:lsb] wand_variable_list; 
   Wor [msb:lsb] wor_variable_list; 
   Tri [msb:lsb] tri_variable_list;

登録

reg（レジスタ）はデータオブジェクトであり、ある手続き型割り当てから次の割り当てへの値を保持し、さまざまな関数および手続き型ブロックでのみ使用されます。regは、単純なVerilogの可変型レジスタであり、物理レジスタを意味することはできません。マルチビットレジスタでは、データは符号なし数値の形式で格納され、符号拡張は使用されません。

例-

reg c; //単一の1ビットレジスタ変数

reg [5：0] gem; // 6ビットのベクトル;

reg [6：0] d、e; // 2つの7ビット変数

入力、出力、入出力

これらのキーワードは、タスクまたはモジュールの入力、出力、および双方向ポートを宣言するために使用されます。ここで、入力ポートと入出力ポートはワイヤタイプであり、出力ポートはワイヤ、reg、ワンド、ワー、またはトライタイプであるように構成されています。常に、デフォルトはワイヤタイプです。

Example

Module sample(a, c, b, d);  
Input c;   // An input where wire is used. 

Output a, b;  // Two outputs where wire is used. 
Output [2:0] d;  /* A three-bit output. One must declare type in a separate statement. */ 
reg [1:0] a;  // The above ‘a’ port is for declaration in reg.

整数

整数は汎用変数で使用されます。これらは主にループで使用されます-インデックス、定数、およびパラメーター。それらは「reg」タイプのデータ型です。これらはデータを符号付き数値として格納しますが、明示的に宣言されたregタイプはそれらを符号なしデータとして格納します。コンパイル時に整数が定義されていない場合、デフォルトのサイズは32ビットになります。

整数が定数を保持している場合、シンセサイザーはコンパイル時に必要な最小幅にそれらを調整します。

Example

Integer c;   // single 32-bit integer 
Assign a = 63;  // 63 defaults to a 7-bit variable.

Supply0、Supply1

Supply0はロジック0（アース）に接続されたワイヤを定義し、supply1はロジック1（電源）に接続されたワイヤを定義します。

Example

supply0 logic_0_wires; 
supply0 gnd1;  // equivalent to a wire assigned as 0 

supply1 logic_1_wires; 
supply1 c, s;

時間

時間は64ビットの量であり、シミュレーション時間を保持するために$ timeシステムタスクと組み合わせて使用​​できます。時間は合成ではサポートされていないため、シミュレーションの目的でのみ使用されます。

Example

time time_variable_list; 
time c; 
c = $time;   //c = current simulation time

パラメータ

パラメータは、モジュールを使用するときに設定できる定数を定義します。これにより、インスタンス化プロセス中にモジュールをカスタマイズできます。

Example 
Parameter add = 3’b010, sub = 2’b11; 
Parameter n = 3; 
Parameter [2:0] param2 = 3’b110; 

reg [n-1:0] jam; /* A 3-bit register with length of n or above. */ 
always @(z) 
y = {{(add - sub){z}};  

if (z)
begin 
   state = param2[1];
else
   state = param2[2]; 
end

演算子

算術演算子

これらの演算子は算術演算を実行します。+および-は、単項（x）またはバイナリ（z-y）演算子として使用されます。

算術演算に含まれる演算子は次のとおりです。

+（加算）、-（減算）、*（乗算）、/（除算）、％（モジュラス）

Example −

parameter v = 5;
reg[3:0] b, d, h, i, count; 
h = b + d; 
i = d - v; 
cnt = (cnt +1)%16; //Can count 0 thru 15.

関係演算子

これらの演算子は2つのオペランドを比較し、結果を1ビットまたは0で返します。

Wire変数とreg変数は正です。したがって、（-3'd001）= = 3'd111および（-3b001）> 3b110です。

関係演算に含まれる演算子は次のとおりです。

• ==（等しい）
• ！=（等しくない）
• >（より大きい）
• > =（以上）
• <（未満）
• <=（以下）

Example

if (z = = y) c = 1; 
   else c = 0; // Compare in 2’s compliment; d>b 
reg [3:0] d,b; 

if (d[3]= = b[3]) d[2:0] > b[2:0]; 
   else b[3]; 
Equivalent Statement 
e = (z == y);

ビット単位の演算子

2つのオペランド間でビットごとの比較を行うビット単位の演算子。

ビット演算に含まれる演算子は次のとおりです。

• ＆（ビットごとのAND）
• | （bitwiseOR）
• 〜（ビット単位ではありません）
• ^（ビット単位のXOR）
• 〜^または^〜（ビット単位のXNOR）

Example

module and2 (d, b, c); 
input [1:0] d, b; 
output [1:0] c; 
assign c = d & b; 
end module

論理演算子

論理演算子はビット単位の演算子であり、シングルビットオペランドにのみ使用されます。これらは、0または1の単一ビット値を返します。整数またはビットのグループ、式を処理し、ゼロ以外のすべての値を1として扱います。論理演算子は、式を処理するため、通常、条件ステートメントで使用されます。

論理演算に含まれる演算子は次のとおりです。

• ！（論理否定）
• &&（論理積）
• || （論理OR）

Example

wire[7:0] a, b, c; // a, b and c are multibit variables. 
reg x; 

if ((a == b) && (c)) x = 1; //x = 1 if a equals b, and c is nonzero. 
   else x = !a; // x =0 if a is anything but zero.

削減演算子

リダクション演算子はビット単位演算子の単項形式であり、オペランドベクトルのすべてのビットを操作します。これらもシングルビット値を返します。

リダクション操作に含まれる演算子は次のとおりです。

• ＆（削減AND）
• | （削減または）
• 〜＆（リダクションNAND）
• 〜| （削減NOR）
• ^（削減XOR）
• 〜^または^〜（縮小XNOR）

Example

Module chk_zero (x, z); 

Input [2:0] x; 
Output z; 
Assign z = & x; // Reduction AND 
End module

シフト演算子

構文の第2オペランドで指定されたビット数だけ第1オペランドをシフトするシフト演算子。空いている位置は、左右のシフトの両方向でゼロで埋められます（使用記号拡張はありません）。

Shift操作に含まれる演算子は次のとおりです。

• <<（左シフト）
• >>（右シフト）

Example

Assign z = c << 3; /* z = c shifted left 3 bits;

空いている位置は0で埋められます* /

連結演算子

連結演算子は、2つ以上のオペランドを組み合わせて、より大きなベクトルを形成します。

連結演算に含まれる演算子は− {}（連結）です。

Example

wire [1:0] a, h; wire [2:0] x; wire [3;0] y, Z; 
assign x = {1’b0, a}; // x[2] = 0, x[1] = a[1], x[0] = a[0] 
assign b = {a, h}; /* b[3] = a[1], b[2] = a[0], b[1] = h[1], 
b[0] = h[0] */ 
assign {cout, b} = x + Z; // Concatenation of a result

レプリケーション演算子

レプリケーションオペレータは、アイテムの複数のコピーを作成しています。

レプリケーション操作で使用される演算子は、-{n {item}}（アイテムのn回のレプリケーション）です。

Example

Wire [1:0] a, f; wire [4:0] x; 
Assign x = {2{1’f0}, a}; // Equivalent to x = {0,0,a } 
Assign y = {2{a}, 3{f}}; //Equivalent to y = {a,a,f,f} 
For synthesis, Synopsis did not like a zero replication.

For example:- 
Parameter l = 5, k = 5; 
Assign x = {(l-k){a}}

条件付き演算子

条件演算子はマルチプレクサに合成します。これはC / C ++で使用されるものと同じ種類であり、条件に基づいて2つの式のいずれかを評価します。

条件付き演算で使用される演算子は-です。

（状態） ？（条件が真の場合の結果）-

（条件がfalseの場合の結果）

Example

Assign x = (g) ? a : b; 
Assign x = (inc = = 2) ? x+1 : x-1; 
/* if (inc), x = x+1, else x = x-1 */

オペランド

リテラル

リテラルは、Verilog式で使用される定数値のオペランドです。一般的に使用される2つのVerilogリテラルは次のとおりです。

• String −文字列リテラルオペランドは、文字の1次元配列であり、二重引用符（ ""）で囲まれています。

• Numeric −定数オペランドは、2進数、8進数、10進数、または16進数で指定されます。

Example

n −ビット数を表す整数

F − 4つの可能な基本フォーマットの1つ−

bは2進数、oは8進数、dは10進数、hは16進数です。

“time is”  // string literal 
267        // 32-bit decimal number 
2’b01      // 2-bit binary 
20’hB36F   // 20-bit hexadecimal number 
‘062       // 32-bit octal number

ワイヤ、登録、およびパラメータ

ワイヤ、レジスタ、およびパラメータは、Verilog式のオペランドとして使用されるデータ型です。

ビット選択「x [2]」およびパート選択「x [4：2]」

ビット選択と部分選択は、角括弧「[]」を使用して、ワイヤ、レジスタ、またはパラメータベクトルからそれぞれ1ビットと複数ビットを選択するために使用されます。ビット選択と部分選択も、メインのデータオブジェクトが使用されるのと同じ方法で、式のオペランドとして使用されます。

Example

reg [7:0] x, y; 
reg [3:0] z; 
reg a; 
a = x[7] & y[7];      // bit-selects 
z = x[7:4] + y[3:0];  // part-selects

関数呼び出し

関数呼び出しでは、関数の戻り値は、最初にレジスターまたはワイヤーに割り当てる必要なしに、式で直接使用されます。関数呼び出しをオペランドのタイプの1つとして配置するだけです。関数呼び出しの戻り値のビット幅を知っていることを確認する必要があります。

Example  
Assign x = y & z & chk_yz(z, y); // chk_yz is a function 

. . ./* Definition of the function */ 
Function chk_yz; // function definition 
Input z,y; 
chk_yz = y^z; 
End function

モジュール

モジュール宣言

Verilogでは、モジュールが主要な設計エンティティです。これは、名前とポートリスト（引数）を示します。次の数行は、各ポートの入力/出力タイプ（入力、出力、または入力）と幅を指定します。デフォルトのポート幅はわずか1ビットです。ポート変数は、wire、wand、。で宣言する必要があります。。。、reg。デフォルトのポート変数はwireです。通常、入力はデータがモジュールの外部でラッチされるため、有線です。信号が内部に格納されている場合、出力はregタイプです。

Example

module sub_add(add, in1, in2, out); 
input add; // defaults to wire 
input [7:0] in1, in2; wire in1, in2; 

output [7:0] out; reg out; 
... statements ... 
End module

継続的な割り当て

モジュール内の連続割り当ては、ワイヤに値を割り当てるために使用されます。これは、alwaysブロックまたは初期ブロックの外側で使用される通常の割り当てです。この割り当ては、明示的な割り当てステートメントを使用するか、宣言中にワイヤに値を割り当てるために行われます。シミュレーション時に連続代入を連続実行します。割り当てステートメントの順序は影響しません。右側の入力信号のいずれかを変更すると、左側の出力信号が変更されます。

Example

Wire [1:0] x = 2’y01;   // assigned on declaration 
Assign y = c | d;       // using assign statement 
Assign d = a & b; 
/* the order of the assign statements does not matter. */

モジュールのインスタンス化

モジュール宣言は、実際のオブジェクトを作成するためのテンプレートです。モジュールは他のモジュール内でインスタンス化され、各インスタンス化はそのテンプレートから単一のオブジェクトを作成します。例外は、独自のインスタンス化であるトップレベルモジュールです。モジュールのポートは、テンプレートで定義されているポートと一致している必要があります。指定されています−

• By name、ドット「.templateポート名（ポートに接続されているワイヤの名前）」を使用します。または

• By position、テンプレートとインスタンスの両方のポートリストの同じ場所にポートを配置します。

Example

MODULE DEFINITION 
Module and4 (x, y, z); 
Input [3:0] x, y; 
Output [3:0] z; 
Assign z = x | y; 
End module

Verilogの動作モデルには、シミュレーションを制御し、データ型の変数を操作する手続き型ステートメントが含まれています。これらのすべてのステートメントは、プロシージャ内に含まれています。各手順には、アクティビティフローが関連付けられています。

動作モデルのシミュレーション中、「always」ステートメントと「initial」ステートメントで定義されたすべてのフローは、シミュレーション時間「zero」で一緒に開始されます。最初のステートメントは1回実行され、alwaysステートメントは繰り返し実行されます。このモデルでは、レジスタ変数aとbは、シミュレーション時間「ゼロ」でそれぞれバイナリ1と0に初期化されます。その後、最初のステートメントが完了し、シミュレーションの実行中に再度実行されることはありません。この最初のステートメントには、ステートメントの開始-終了ブロック（順次ブロックとも呼ばれます）が含まれています。この開始-終了タイプのブロックでは、aが最初に初期化され、次にbが初期化されます。

行動モデリングの例

module behave; 
reg [1:0]a,b; 

initial 
begin 
   a = ’b1; 
   b = ’b0; 
end 

always 
begin 
   #50 a = ~a; 
end 

always 
begin 
   #100 b = ~b; 
end 
End module

手続き上の割り当て

手続き型の割り当ては、reg、integer、time、およびmemory変数を更新するためのものです。以下に説明するように、手続き型割り当てと連続割り当ての間には大きな違いがあります。

連続割り当てはネット変数を駆動し、入力オペランドが値を変更するたびに評価および更新されます。

手続き型割り当ては、レジスタ変数を囲む手続き型フロー構造の制御下でレジスタ変数の値を更新します。

手続き型代入の右辺は、値に評価される任意の式にすることができます。ただし、右側の部分選択には定数インデックスが必要です。左側は、右側から割り当てを受け取る変数を示します。手続き型割り当ての左側は、次のいずれかの形式を取ることができます-

• レジスター、整数、実数、または時間変数-これらのデータ型の1つの名前参照への割り当て。

• レジスタ、整数、実数、または時間変数のビット選択-他のビットをそのままにしておく単一ビットへの割り当て。

• レジスタ、整数、実数、または時間変数の部分選択-残りのビットをそのままにしておく2つ以上の連続するビットの部分選択。部分選択形式の場合、定数式のみが有効です。

• メモリ要素-メモリの1ワード。ビット選択と部分選択は、メモリ要素の参照では無効であることに注意してください。

• 上記のいずれかの連結-前の4つの形式のいずれかの連結を指定できます。これにより、右辺の式の結果が効果的に分割され、分割部分が順番に連結のさまざまな部分に割り当てられます。

割り当ての遅延（合成用ではありません）

遅延割り当てでは、ステートメントが実行されて左側の割り当てが行われる前に、Δt時間単位が経過します。割り当て内遅延を使用すると、右側がすぐに評価されますが、結果が左側の割り当てに配置されるまでにΔtの遅延があります。Δt中に別の手順で右側の信号が変更されても、出力には影響しません。遅延は合成ツールではサポートされていません。

構文

• Procedural Assignment変数=式

• Delayed assignment＃Δt変数=式;

• Intra-assignment delay変数=＃Δt式;

例

reg [6:0] sum; reg h, ziltch; 
sum[7] = b[7] ^ c[7]; // execute now. 
ziltch = #15 ckz&h; /* ckz&a evaluated now; ziltch changed 
after 15 time units. */ 

#10 hat = b&c; /* 10 units after ziltch changes, b&c is
evaluated and hat changes. */

割り当てのブロック

ブロッキング手続き型割り当てステートメントは、シーケンシャルブロックでそれに続くステートメントを実行する前に実行する必要があります。ブロッキング手続き型割り当てステートメントは、並列ブロックでそれに続くステートメントの実行を妨げません。

構文

ブロッキング手続き型割り当ての構文は次のとおりです。

<lvalue> = <timing_control> <expression>

ここで、lvalueは手続き型代入ステートメントに有効なデータ型、=は代入演算子、タイミング制御はオプションの代入内遅延です。タイミング制御遅延は、遅延制御（たとえば、＃6）またはイベント制御（たとえば、@（posedge clk））のいずれかです。式は、シミュレーターが左側に割り当てる右側の値です。手続き型代入をブロックすることによって使用される=代入演算子は、手続き型連続代入および連続代入でも使用されます。

例

rega = 0; 
rega[3] = 1;            // a bit-select 
rega[3:5] = 7;          // a part-select 
mema[address] = 8’hff;  // assignment to a memory element 
{carry, acc} = rega + regb;  // a concatenation

ノンブロッキング（RTL）割り当て

非ブロッキング手続き型割り当てを使用すると、手続き型フローをブロックせずに割り当てをスケジュールできます。順序や相互依存関係に関係なく、同じタイムステップ内で複数のレジスタ割り当てを行いたい場合はいつでも、ノンブロッキング手続き型ステートメントを使用できます。

構文

ノンブロッキング手続き型割り当ての構文は次のとおりです。

<lvalue> <= <timing_control> <expression>

lvalueが手続き型代入ステートメントに有効なデータ型である場合、<=は非ブロッキング代入演算子であり、タイミング制御はオプションの代入内タイミング制御です。タイミング制御遅延は、遅延制御またはイベント制御のいずれかです（たとえば、@（posedge clk））。式は、シミュレーターが左側に割り当てる右側の値です。ノンブロッキング代入演算子は、シミュレーターが等しくない関係演算子に使用するのと同じ演算子です。シミュレーターは、式で使用する場合は<=演算子を関係演算子として解釈し、非ブロッキング手続き型代入構造で使用する場合は<=演算子を代入演算子として解釈します。

シミュレーターが非ブロッキング手続き型割り当てを評価する方法シミュレーターが非ブロッキング手続き型割り当てに遭遇すると、シミュレーターは次の2つのステップで非ブロッキング手続き型割り当てを評価して実行します。

• シミュレータは右側を評価し、手続き型タイミング制御で指定された時間に新しい値の割り当てが行われるようにスケジュールします。シミュレータは右側を評価し、手続き型タイミング制御で指定された時間に新しい値の割り当てが行われるようにスケジュールします。

• 指定された遅延が期限切れになった、または適切なイベントが発生したタイムステップの終了時に、シミュレータは値を左側に割り当てることによって割り当てを実行します。

例

module evaluates2(out); 
output out; 
reg a, b, c; 
initial 

begin 
   a = 0; 
   b = 1; 
   c = 0; 
end 
always c = #5 ~c; 
always @(posedge c) 

begin 
   a <= b; 
   b <= a; 
end 
endmodule

条件

条件ステートメント（またはif-elseステートメント）は、ステートメントが実行されるかどうかを決定するために使用されます。

正式には、構文は次のとおりです。

<statement> 
::= if ( <expression> ) <statement_or_null> 
||= if ( <expression> ) <statement_or_null> 
   else <statement_or_null> 
<statement_or_null> 

::= <statement> 
||= ;

<式>が評価されます。trueの場合（つまり、既知の値がゼロ以外の場合）、最初のステートメントが実行されます。falseの場合（値がゼロであるか、値がxまたはzの場合）、最初のステートメントは実行されません。elseステートメントがあり、<expression>がfalseの場合、elseステートメントが実行されます。if式の数値がゼロであるかどうかがテストされるため、特定のショートカットが可能です。

たとえば、次の2つのステートメントは同じロジックを表します-

if (expression) 
if (expression != 0)

if-elseのelse部分はオプションであるため、ネストされたifシーケンスからelseが省略されると、混乱が生じる可能性があります。これは、elseがない場合は、常にelseを最も近い前の値に関連付けることで解決されます。

例

if (index > 0) 
if (rega > regb) 
   result = rega; 
   else // else applies to preceding if 
   result = regb; 

If that association is not what you want, use a begin-end block statement 
to force the proper association 

if (index > 0) 
begin 

if (rega > regb) 
result = rega; 
end 
   else 
   result = regb;

の構築：if- else- if

次の構造は非常に頻繁に発生するため、簡単に個別に説明する価値があります。

Example

if (<expression>) 
   <statement> 
   else if (<expression>) 
   <statement> 
   else if (<expression>) 
   <statement> 
   else  
   <statement>

この一連のif（if-else-if構文として知られている）は、多方向の決定を記述する最も一般的な方法です。式は順番に評価されます。いずれかの式がtrueの場合、それに関連付けられたステートメントが実行され、これによりチェーン全体が終了します。各ステートメントは、単一のステートメントまたはステートメントのブロックのいずれかです。

if-else-if構文の最後のelse部分は、「上記のいずれでもない」または他の条件のいずれも満たされないデフォルトのケースを処理します。デフォルトの明示的なアクションがない場合があります。その場合、末尾のelseを省略したり、エラーチェックに使用して不可能な状態をキャッチしたりできます。

ケースステートメント

caseステートメントは、式が他の多くの式の1つと一致するかどうかをテストし、それに応じて分岐する特別な多方向決定ステートメントです。caseステートメントは、たとえばマイクロプロセッサ命令のデコードを説明するのに役立ちます。caseステートメントの構文は次のとおりです-

Example

<statement> 
::= case ( <expression> ) <case_item>+ endcase 
||= casez ( <expression> ) <case_item>+ endcase 
||= casex ( <expression> ) <case_item>+ endcase 
<case_item> 
::= <expression> <,<expression>>* : <statement_or_null> 
||= default : <statement_or_null> 
||= default <statement_or_null>

ケース式は、指定された正確な順序で評価および比較されます。線形検索中に、ケースアイテムの式の1つが括弧内の式と一致する場合、そのケースアイテムに関連付けられたステートメントが実行されます。すべての比較が失敗し、デフォルトのアイテムが指定されている場合、デフォルトのアイテムステートメントが実行されます。デフォルトのステートメントが指定されておらず、すべての比較が失敗した場合、caseitemステートメントは実行されません。

構文とは別に、caseステートメントは2つの重要な点で多方向if-else-if構文とは異なります-

• if-else-if構文の条件式は、caseステートメントのように、1つの式を他の複数の式と比較するよりも一般的です。

• 式にx値とz値がある場合、caseステートメントは決定的な結果を提供します。

ループステートメント

ループステートメントには4つのタイプがあります。これらは、ステートメントの実行を0回、1回、またはそれ以上制御する手段を提供します。

• 永久にステートメントを継続的に実行します。

• repeatは、ステートメントを一定の回数実行します。

• whileは、式がfalseになるまでステートメントを実行します。式がfalseで始まる場合、ステートメントはまったく実行されません。

• 次のように、3ステップのプロセスによって関連するステートメントの実行を制御します。

  • 実行されるループの数を制御する変数を初期化するために通常使用される割り当てを実行します

  • 式を評価します。結果がゼロの場合、forループは終了し、ゼロでない場合、forループは関連するステートメントを実行してから、手順3を実行します。

  • ループ制御変数の値を変更するために通常使用される割り当てを実行してから、ステップ2を繰り返します。

ループステートメントの構文規則は次のとおりです-

Example

<statement> 
::= forever <statement> 
||=forever 
begin 
   <statement>+ 
end  

<Statement> 
::= repeat ( <expression> ) <statement> 
||=repeat ( <expression> ) 
begin
   <statement>+ 
end  

<statement> 
::= while ( <expression> ) <statement> 
||=while ( <expression> ) 
begin 
   <statement>+ 
end  
<statement> 
::= for ( <assignment> ; <expression> ; <assignment> ) 
<statement> 
||=for ( <assignment> ; <expression> ; <assignment> ) 
begin 
   <statement>+ 
end

遅延制御

遅延制御

手続き型ステートメントの実行は、次の構文を使用して遅延制御できます。

<statement> 
::= <delay_control> <statement_or_null> 
<delay_control> 
::= # <NUMBER> 
||= # <identifier> 
||= # ( <mintypmax_expression> )

次の例では、割り当ての実行を10時間単位遅らせます-

＃10 rega = regb;

次の3つの例は、番号記号（＃）に続く式を提供します。割り当ての実行は、式の値で指定されたシミュレーション時間だけ遅延します。

イベント制御

手続き型ステートメントの実行は、次のイベント制御構文を使用して、ネットまたはレジスタの値の変更、または宣言されたイベントの発生と同期させることができます。

Example

<statement> 
::= <event_control> <statement_or_null> 

<event_control> 
::= @ <identifier> 
||= @ ( <event_expression> ) 

<event_expression> 
::= <expression> 
||= posedge <SCALAR_EVENT_EXPRESSION> 
||= negedge <SCALAR_EVENT_EXPRESSION> 
||= <event_expression> <or <event_expression>>

* <SCALAR_EVENT_EXPRESSION>は、1ビット値に解決される式です。

ネットとレジスタの値の変更は、ステートメントの実行をトリガーするイベントとして使用できます。これは、暗黙的なイベントの検出として知られています。Verilog構文では、変更の方向に基づいて変更を検出することもできます。つまり、値1（ポーズ）または値0（ネガ）に向かっています。未知の式の値に対するポーズとネゲッジの動作は次のとおりです。

• 1から不明への遷移および不明から0への遷移でネガエッジが検出されます
• ポーズは、0から不明への遷移および不明から1への遷移で検出されます

手順：常に最初のブロック

Verilogのすべてのプロシージャは、次の4つのブロックのいずれかで指定されます。1）初期ブロック2）常にブロック3）タスク4）機能

初期ステートメントとalwaysステートメントは、シミュレーションの開始時に有効になります。最初のブロックは1回だけ実行され、ステートメントが終了するとそのアクティビティは終了します。対照的に、alwaysブロックは繰り返し実行されます。そのアクティビティは、シミュレーションが終了したときにのみ停止します。モジュールで定義できる初期ブロックと常にブロックの数に制限はありません。タスクと機能は、他の手順の1つ以上の場所から有効になる手順です。

初期ブロック

最初のステートメントの構文は次のとおりです-

<initial_statement> 
::= initial <statement>

次の例は、シミュレーションの開始時に変数を初期化するための初期ステートメントの使用を示しています。

Initial 
Begin 
   Areg = 0; // initialize a register 
   For (index = 0; index < size; index = index + 1) 
   Memory [index] = 0; //initialize a memory 
   Word 
End

初期ブロックのもう1つの一般的な使用法は、シミュレートされる回路の主要部分に刺激を提供するために1回実行される波形記述の指定です。

Initial 
Begin 
   Inputs = ’b000000; 
   // initialize at time zero 
   #10 inputs = ’b011001; // first pattern 
   #10 inputs = ’b011011; // second pattern 
   #10 inputs = ’b011000; // third pattern 
   #10 inputs = ’b001000; // last pattern 
End

常にブロック

'always'ステートメントは、シミュレーションの実行全体を通して継続的に繰り返されます。alwaysステートメントの構文を以下に示します。

<always_statement> 
::= always <statement>

'always'ステートメントは、ループの性質があるため、何らかの形式のタイミング制御と組み合わせて使用​​した場合にのみ役立ちます。'always'ステートメントが前進する時間を提供しない場合、 'always'ステートメントはシミュレーションのデッドロック状態を作成します。たとえば、次のコードは、無限のゼロ遅延ループを作成します-

Always areg = ~areg;

上記のコードにタイミング制御を提供すると、次の例のように、潜在的に有用な説明が作成されます。

Always #half_period areg = ~areg;