빠른 가이드
현대 전자 세계에서 용어 Digital 일반적으로 컴퓨터와 관련이 있습니다. Digital숫자를 세어 컴퓨터가 작업을 수행하는 방식에서 파생됩니다. 수년 동안 디지털 전자 장치의 응용은 컴퓨터 시스템에만있었습니다. 그러나 오늘날 디지털 전자는 다른 많은 응용 분야에서 사용됩니다. 다음은 몇 가지 예입니다.Digital electronics 많이 사용됩니다.
- 산업 공정 제어
- 군사 시스템
- Television
- 의사 소통 시스템
- 의료 장비
- Radar
- Navigation
신호
Signal일부 정보를 포함하는 물리량으로 정의 할 수 있습니다. 하나 이상의 독립 변수의 함수입니다. 신호는 두 가지 유형이 있습니다.
- 아날로그 신호
- 디지털 신호
아날로그 신호
안 analog signal연속적인 값을 갖는 신호로 정의됩니다. 아날로그 신호는 무한한 수의 다른 값을 가질 수 있습니다. 실제 시나리오에서 자연에서 관찰되는 대부분의 것은 아날로그입니다. 아날로그 신호의 예는 다음과 같습니다.
- Temperature
- Pressure
- Distance
- Sound
- Voltage
- Current
- Power
아날로그 신호의 그래픽 표현 (온도)
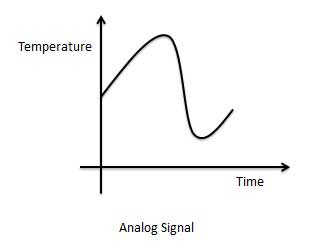
아날로그 신호를 처리하는 회로를 아날로그 회로 또는 시스템이라고합니다. 아날로그 시스템의 예는 다음과 같습니다.
- Filter
- Amplifiers
- 텔레비전 수신기
- 모터 속도 컨트롤러
아날로그 시스템의 단점
- 덜 정확도
- 덜 다재다능 함
- 더 많은 소음 효과
- 더 많은 왜곡
- 날씨의 더 많은 영향
디지털 신호
ㅏ digital signal한정된 수의 고유 값만있는 신호로 정의됩니다. 디지털 신호는 연속 신호가 아닙니다. 디지털 전자 계산기에서 입력은 스위치를 사용하여 제공됩니다. 이 입력은 두 개의 개별 값 또는 레벨이있는 전기 신호로 변환됩니다. 이들 중 하나는 로우 레벨이라고 할 수 있고 다른 하나는 하이 레벨이라고 할 수 있습니다. 신호는 항상 두 레벨 중 하나입니다. 이러한 유형의 신호를 디지털 신호라고합니다. 디지털 신호의 예는 다음과 같습니다.
- 이진 신호
- 8 진법 신호
- 16 진수 신호
디지털 신호의 그래픽 표현 (바이너리)
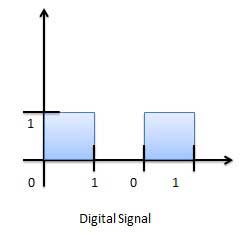
디지털 신호를 처리하는 회로를 디지털 시스템 또는 디지털 회로라고합니다. 디지털 시스템의 예는 다음과 같습니다.
- Registers
- Flip-flop
- Counters
- Microprocessors
디지털 시스템의 장점
- 더 많은 정확성
- 더 다양한 기능
- 덜 왜곡
- 쉬운 의사 소통
- 정보 저장 가능
아날로그 및 디지털 신호 비교
| SN | 아날로그 신호 | 디지털 신호 |
|---|---|---|
| 1 | 아날로그 신호에는 무한한 값이 있습니다. | 디지털 신호에는 유한 한 수의 값이 있습니다. |
| 2 | 아날로그 신호는 연속적인 특성을 가지고 있습니다. | 디지털 신호는 불연속적인 특성을 가지고 있습니다. |
| 삼 | 아날로그 신호는 변환기와 신호 발생기에 의해 생성됩니다. | 디지털 신호는 A-D 변환기에 의해 생성됩니다. |
| 4 | 아날로그 신호의 예-사인파, 삼각파. | 디지털 신호의 예-이진 신호. |
디지털 시스템은 숫자라는 기호가 몇 개있는 경우에만 위치 번호 시스템을 이해할 수 있으며 이러한 기호는 숫자에서 차지하는 위치에 따라 다른 값을 나타냅니다.
숫자의 각 자릿수 값은 다음을 사용하여 결정할 수 있습니다.
숫자
숫자에서 숫자의 위치
숫자 체계의 기수 (여기서 기수는 숫자 체계에서 사용 가능한 총 자릿수로 정의 됨).
십진수 체계
우리가 일상 생활에서 사용하는 숫자 체계는 십진수 체계입니다. 10 진수 시스템은 0부터 9까지 10 자리를 사용하므로 밑 수가 10입니다. 10 진수 시스템에서 소수점 왼쪽의 연속 된 위치는 단위, 수십, 수백, 수천 등을 나타냅니다.
각 위치는베이스 (10)의 특정 힘을 나타냅니다. 예를 들어, 10 진수 1234는 단위 위치의 숫자 4, 10 위치의 3, 수백 위치의 2, 천 위치의 1로 구성되며 그 값은 다음과 같이 쓸 수 있습니다.
(1×1000) + (2×100) + (3×10) + (4×l)
(1×103) + (2×102) + (3×101) + (4×l00)
1000 + 200 + 30 + 1
1234컴퓨터 프로그래머 또는 IT 전문가는 컴퓨터에서 자주 사용되는 다음 숫자 체계를 이해해야합니다.
| SN | 번호 체계 및 설명 |
|---|---|
| 1 | Binary Number System 기본 2. 사용 된 숫자 : 0, 1 |
| 2 | Octal Number System 기본 8. 사용 된 숫자 : 0 ~ 7 |
| 삼 | Hexa Decimal Number System 기본 16. 사용 된 숫자 : 0 ~ 9, 사용 된 문자 : A-F |
이진수 시스템
형질
두 자리, 0과 1을 사용합니다.
base 2 number system이라고도 함
이진수의 각 위치는 밑 (2)의 0 거듭 제곱을 나타냅니다. 예 : 2 0
이진수의 마지막 위치는 밑 (2)의 x 거듭 제곱을 나타냅니다. 예 : 2 x 여기서 x는 마지막 위치-1을 나타냅니다.
예
이진수 : 10101 2
등가 십진수 계산 −
| 단계 | 이진수 | 십진수 |
|---|---|---|
| 1 단계 | 10101 2 | ((1 × 2 4 ) + (0 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 )) 10 |
| 2 단계 | 10101 2 | (16 + 0 + 4 + 0 + 1) 10 |
| 3 단계 | 10101 2 | 21 10 |
Note:10101 2 는 일반적으로 10101로 작성됩니다.
8 진법
형질
8 자리 숫자 0,1,2,3,4,5,6,7을 사용합니다.
8 진법이라고도 함
8 진수의 각 위치는 밑수 (8)의 0 거듭 제곱을 나타냅니다. 예 : 8 0
8 진수의 마지막 위치는 밑 (8)의 x 거듭 제곱을 나타냅니다. 예 : 8 x 여기서 x는 마지막 위치-1을 나타냅니다.
예
8 진수 − 12570 8
등가 십진수 계산 −
| 단계 | 8 진수 | 십진수 |
|---|---|---|
| 1 단계 | 12570 8 | ((1 × 8 (4) ) + (2 × 8 (3) ) + (5 × 8 2 ) + (8 × 7 (1) ) + (0 × 8 0 )) 10 |
| 2 단계 | 12570 8 | (4096 + 1024 + 320 + 56 + 0) 10 |
| 3 단계 | 12570 8 | 5496 10 |
Note:12570 8 은 일반적으로 12570으로 작성됩니다.
16 진수 시스템
형질
10 자리 숫자와 6 자리 문자 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F를 사용합니다.
문자는 10부터 시작하는 숫자를 나타냅니다. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
16 진수 시스템이라고도합니다.
16 진수의 각 위치는 밑수 (16)의 0 거듭 제곱을 나타냅니다. 예제 16 0 .
16 진수의 마지막 위치는 밑수 (16)의 x 거듭 제곱을 나타냅니다. 예 16 x 여기서 x는 마지막 위치-1을 나타냅니다.
예-
16 진수 : 19FDE 16
등가 십진수 계산 −
| 단계 | 16 진수 | 십진수 |
|---|---|---|
| 1 단계 | 19FDE 16 | ((1 × 16 4 ) + (8 × 16 3 ) + (F × 16 (2) ) + (D × 16 1 ) + (16 × E 0 )) 10 |
| 2 단계 | 19FDE 16 | ((1 × 16 4 ) + (8 × 16 3 ) + (15 × 16 (2) ) + (13 × 16 1 ) + (14 × 16 0 )) 10 |
| 3 단계 | 19FDE 16 | (65536 + 36864 + 3840 + 208 + 14) 10 |
| 4 단계 | 19FDE 16 | 106462 10 |
Note −19FDE 16 은 일반적으로 19FDE로 작성됩니다.
한 염기에서 다른 염기로 숫자를 변환하는 데 사용할 수있는 많은 방법이나 기술이 있습니다. 여기에서 다음을 시연합니다.
- 다른 기본 시스템에 대한 10 진수
- 기타 기본 시스템을 10 진수로
- 10 진수가 아닌 다른 기본 시스템
- 바로 가기 방법-2 진수에서 8 진수로
- 바로 가기 방법-8 진법에서 2 진법
- 바로 가기 방법-2 진수에서 16 진수로
- 바로 가기 방법-16 진수를 2 진수로
다른 기본 시스템에 대한 10 진수
단계
Step 1 − 변환 할 10 진수를 새 밑수로 나눕니다.
Step 2 − 1 단계의 나머지를 새 기본 번호의 가장 오른쪽 자리 (최하위 자리)로 가져옵니다.
Step 3 − 이전 나누기의 몫을 새 밑으로 나눕니다.
Step 4 − 3 단계의 나머지를 새 기본 번호의 다음 숫자 (왼쪽)로 기록합니다.
3 단계에서 몫이 0이 될 때까지 나머지를 오른쪽에서 왼쪽으로 가져와 3 단계와 4 단계를 반복합니다.
이렇게 얻은 마지막 나머지는 새 기본 번호의 MSD (Most Significant Digit)가됩니다.
예-
10 진수 : 29 10
이진 등가 계산 −
| 단계 | 조작 | 결과 | 나머지 |
|---|---|---|---|
| 1 단계 | 29/2 | 14 | 1 |
| 2 단계 | 14/2 | 7 | 0 |
| 3 단계 | 7/2 | 삼 | 1 |
| 4 단계 | 3/2 | 1 | 1 |
| 5 단계 | 1/2 | 0 | 1 |
2 단계와 4 단계에서 언급했듯이 나머지는 첫 번째 나머지가 LSD (Least Significant Digit)가되고 마지막 나머지가 MSD (Most Significant Digit)가되도록 역순으로 정렬해야합니다.
십진수 − 29 10 = 이진수 − 11101 2 .
기타 기본 시스템에서 10 진수 시스템으로
단계
Step 1 − 각 숫자의 열 (위치) 값을 결정합니다 (숫자의 위치와 숫자 체계의 밑수에 따라 다름).
Step 2 − 획득 한 열 값 (1 단계)에 해당 열의 숫자를 곱합니다.
Step 3 − 2 단계에서 계산 된 제품의 합계를 구하십시오. 합계는 십진수로 표시된 동등한 값입니다.
예
이진수 − 11101 2
등가 십진수 계산 −
| 단계 | 이진수 | 십진수 |
|---|---|---|
| 1 단계 | 11101 2 | ((1 × 2 4 ) + (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 )) 10 |
| 2 단계 | 11101 2 | (16 + 8 + 4 + 0 + 1) 10 |
| 3 단계 | 11101 2 | 29 10 |
이진수 − 11101 2 = 10 진수 − 29 10
기타 기본 시스템에서 10 진수가 아닌 시스템으로
단계
Step 1 − 원래 숫자를 10 진수 (밑수 10)로 변환합니다.
Step 2 − 이렇게 얻은 10 진수를 새로운 기본 숫자로 변환합니다.
예
8 진수 − 25 8
이진 등가 계산 −
1 단계-10 진수로 변환
| 단계 | 8 진수 | 십진수 |
|---|---|---|
| 1 단계 | 25 8 | ((2 × 8 1 ) + (5 × 8 0 )) 10 |
| 2 단계 | 25 8 | (16 + 5) 10 |
| 3 단계 | 25 8 | 21 10 |
8 진수 − 25 8 = 10 진수 − 21 10
2 단계-십진수를 이진수로 변환
| 단계 | 조작 | 결과 | 나머지 |
|---|---|---|---|
| 1 단계 | 21/2 | 10 | 1 |
| 2 단계 | 10/2 | 5 | 0 |
| 3 단계 | 5/2 | 2 | 1 |
| 4 단계 | 2/2 | 1 | 0 |
| 5 단계 | 1/2 | 0 | 1 |
10 진수 − 21 10 = 이진수 − 10101 2
8 진수 − 25 8 = 이진수 − 10101 2
바로 가기 방법-2 진수에서 8 진수로
단계
Step 1 − 이진수를 3 개의 그룹으로 나눕니다 (오른쪽에서 시작).
Step 2 − 3 개의 이진수 그룹을 8 진수 1 개로 변환합니다.
예
이진수 − 10101 2
등가 8 진법 계산 −
| 단계 | 이진수 | 8 진수 |
|---|---|---|
| 1 단계 | 10101 2 | 010101 |
| 2 단계 | 10101 2 | 2 8 5 8 |
| Step 3 | 101012 | 258 |
Binary Number − 101012 = Octal Number − 258
Shortcut method - Octal to Binary
Steps
Step 1 − Convert each octal digit to a 3 digit binary number (the octal digits may be treated as decimal for this conversion).
Step 2 − Combine all the resulting binary groups (of 3 digits each) into a single binary number.
Example
Octal Number − 258
Calculating Binary Equivalent −
| Step | Octal Number | Binary Number |
|---|---|---|
| Step 1 | 258 | 210 510 |
| Step 2 | 258 | 0102 1012 |
| Step 3 | 258 | 0101012 |
Octal Number − 258 = Binary Number − 101012
Shortcut method - Binary to Hexadecimal
Steps
Step 1 − Divide the binary digits into groups of four (starting from the right).
Step 2 − Convert each group of four binary digits to one hexadecimal symbol.
Example
Binary Number − 101012
Calculating hexadecimal Equivalent −
| Step | Binary Number | Hexadecimal Number |
|---|---|---|
| Step 1 | 101012 | 0001 0101 |
| Step 2 | 101012 | 110 510 |
| Step 3 | 101012 | 1516 |
Binary Number − 101012 = Hexadecimal Number − 1516
Shortcut method - Hexadecimal to Binary
Steps
Step 1 − Convert each hexadecimal digit to a 4 digit binary number (the hexadecimal digits may be treated as decimal for this conversion).
Step 2 − Combine all the resulting binary groups (of 4 digits each) into a single binary number.
Example
Hexadecimal Number − 1516
Calculating Binary Equivalent −
| Step | Hexadecimal Number | Binary Number |
|---|---|---|
| Step 1 | 1516 | 110 510 |
| Step 2 | 1516 | 00012 01012 |
| Step 3 | 1516 | 000101012 |
Hexadecimal Number − 1516 = Binary Number − 101012
In the coding, when numbers, letters or words are represented by a specific group of symbols, it is said that the number, letter or word is being encoded. The group of symbols is called as a code. The digital data is represented, stored and transmitted as group of binary bits. This group is also called as binary code. The binary code is represented by the number as well as alphanumeric letter.
Advantages of Binary Code
Following is the list of advantages that binary code offers.
Binary codes are suitable for the computer applications.
Binary codes are suitable for the digital communications.
Binary codes make the analysis and designing of digital circuits if we use the binary codes.
Since only 0 & 1 are being used, implementation becomes easy.
Classification of binary codes
The codes are broadly categorized into following four categories.
- Weighted Codes
- Non-Weighted Codes
- Binary Coded Decimal Code
- Alphanumeric Codes
- Error Detecting Codes
- Error Correcting Codes
Weighted Codes
Weighted binary codes are those binary codes which obey the positional weight principle. Each position of the number represents a specific weight. Several systems of the codes are used to express the decimal digits 0 through 9. In these codes each decimal digit is represented by a group of four bits.
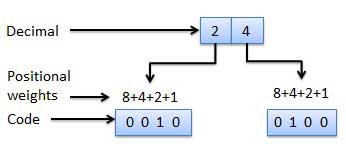
Non-Weighted Codes
In this type of binary codes, the positional weights are not assigned. The examples of non-weighted codes are Excess-3 code and Gray code.
Excess-3 code
The Excess-3 code is also called as XS-3 code. It is non-weighted code used to express decimal numbers. The Excess-3 code words are derived from the 8421 BCD code words adding (0011)2 or (3)10 to each code word in 8421. The excess-3 codes are obtained as follows −

Example
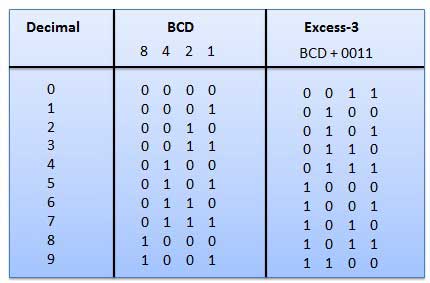
Gray Code
It is the non-weighted code and it is not arithmetic codes. That means there are no specific weights assigned to the bit position. It has a very special feature that, only one bit will change each time the decimal number is incremented as shown in fig. As only one bit changes at a time, the gray code is called as a unit distance code. The gray code is a cyclic code. Gray code cannot be used for arithmetic operation.
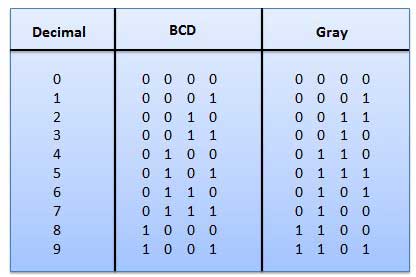
Application of Gray code
Gray code is popularly used in the shaft position encoders.
A shaft position encoder produces a code word which represents the angular position of the shaft.
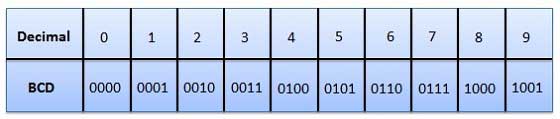
Binary Coded Decimal (BCD) code
In this code each decimal digit is represented by a 4-bit binary number. BCD is a way to express each of the decimal digits with a binary code. In the BCD, with four bits we can represent sixteen numbers (0000 to 1111). But in BCD code only first ten of these are used (0000 to 1001). The remaining six code combinations i.e. 1010 to 1111 are invalid in BCD.
Advantages of BCD Codes
- It is very similar to decimal system.
- We need to remember binary equivalent of decimal numbers 0 to 9 only.
Disadvantages of BCD Codes
The addition and subtraction of BCD have different rules.
The BCD arithmetic is little more complicated.
BCD needs more number of bits than binary to represent the decimal number. So BCD is less efficient than binary.
Alphanumeric codes
A binary digit or bit can represent only two symbols as it has only two states '0' or '1'. But this is not enough for communication between two computers because there we need many more symbols for communication. These symbols are required to represent 26 alphabets with capital and small letters, numbers from 0 to 9, punctuation marks and other symbols.
The alphanumeric codes are the codes that represent numbers and alphabetic characters. Mostly such codes also represent other characters such as symbol and various instructions necessary for conveying information. An alphanumeric code should at least represent 10 digits and 26 letters of alphabet i.e. total 36 items. The following three alphanumeric codes are very commonly used for the data representation.
- American Standard Code for Information Interchange (ASCII).
- Extended Binary Coded Decimal Interchange Code (EBCDIC).
- Five bit Baudot Code.
ASCII code is a 7-bit code whereas EBCDIC is an 8-bit code. ASCII code is more commonly used worldwide while EBCDIC is used primarily in large IBM computers.
Error Codes
There are binary code techniques available to detect and correct data during data transmission.
| Error Code | Description |
|---|---|
Error Detection and Correction |
Error detection and correction code techniques |
There are many methods or techniques which can be used to convert code from one format to another. We'll demonstrate here the following
- Binary to BCD Conversion
- BCD to Binary Conversion
- BCD to Excess-3
- Excess-3 to BCD
Binary to BCD Conversion
Steps
Step 1 -- Convert the binary number to decimal.
Step 2 -- Convert decimal number to BCD.
Example − convert (11101)2 to BCD.
Step 1 − Convert to Decimal
Binary Number − 111012
Calculating Decimal Equivalent −
| Step | Binary Number | Decimal Number |
|---|---|---|
| Step 1 | 111012 | ((1 × 24) + (1 × 23) + (1 × 22) + (0 × 21) + (1 × 20))10 |
| Step 2 | 111012 | (16 + 8 + 4 + 0 + 1)10 |
| Step 3 | 111012 | 2910 |
Binary Number − 111012 = Decimal Number − 2910
Step 2 − Convert to BCD
Decimal Number − 2910
Calculating BCD Equivalent. Convert each digit into groups of four binary digits equivalent.
| Step | Decimal Number | Conversion |
|---|---|---|
| Step 1 | 2910 | 00102 10012 |
| Step 2 | 2910 | 00101001BCD |
Result
(11101)2 = (00101001)BCDBCD to Binary Conversion
Steps
Step 1 -- Convert the BCD number to decimal.
Step 2 -- Convert decimal to binary.
Example − convert (00101001)BCD to Binary.
Step 1 - Convert to BCD
BCD Number − (00101001)BCD
Calculating Decimal Equivalent. Convert each four digit into a group and get decimal equivalent for each group.
| Step | BCD Number | Conversion |
|---|---|---|
| Step 1 | (00101001)BCD | 00102 10012 |
| Step 2 | (00101001)BCD | 210 910 |
| Step 3 | (00101001)BCD | 2910 |
BCD Number − (00101001)BCD = Decimal Number − 2910
Step 2 - Convert to Binary
Used long division method for decimal to binary conversion.
Decimal Number − 2910
Calculating Binary Equivalent −
| Step | Operation | Result | Remainder |
|---|---|---|---|
| Step 1 | 29 / 2 | 14 | 1 |
| Step 2 | 14 / 2 | 7 | 0 |
| Step 3 | 7 / 2 | 3 | 1 |
| Step 4 | 3 / 2 | 1 | 1 |
| Step 5 | 1 / 2 | 0 | 1 |
As mentioned in Steps 2 and 4, the remainders have to be arranged in the reverse order so that the first remainder becomes the least significant digit (LSD) and the last remainder becomes the most significant digit (MSD).
Decimal Number − 2910 = Binary Number − 111012
Result
(00101001)BCD = (11101)2BCD to Excess-3
Steps
Step 1 -- Convert BCD to decimal.
Step 2 -- Add (3)10 to this decimal number.
Step 3 -- Convert into binary to get excess-3 code.
Example − convert (0110)BCD to Excess-3.
Step 1 − Convert to decimal
(0110)BCD = 610
Step 2 − Add 3 to decimal
(6)10 + (3)10 = (9)10
Step 3 − Convert to Excess-3
(9)10 = (1001)2
Result
(0110)BCD = (1001)XS-3Excess-3 to BCD Conversion
Steps
Step 1 -- Subtract (0011)2 from each 4 bit of excess-3 digit to obtain the corresponding BCD code.
Example − convert (10011010)XS-3 to BCD.
Given XS-3 number = 1 0 0 1 1 0 1 0
Subtract (0011)2 = 1 0 0 1 0 1 1 1
--------------------
BCD = 0 1 1 0 0 1 1 1Result
(10011010)XS-3 = (01100111)BCDComplements are used in the digital computers in order to simplify the subtraction operation and for the logical manipulations. For each radix-r system (radix r represents base of number system) there are two types of complements.
| S.N. | Complement | Description |
|---|---|---|
| 1 | Radix Complement | The radix complement is referred to as the r's complement |
| 2 | Diminished Radix Complement | The diminished radix complement is referred to as the (r-1)'s complement |
Binary system complements
As the binary system has base r = 2. So the two types of complements for the binary system are 2's complement and 1's complement.
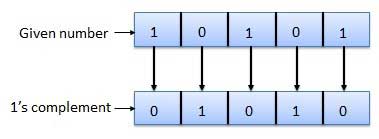
1's complement
The 1's complement of a number is found by changing all 1's to 0's and all 0's to 1's. This is called as taking complement or 1's complement. Example of 1's Complement is as follows.
2's complement
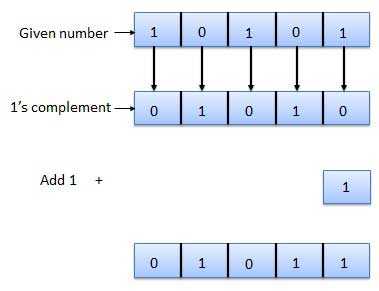
The 2's complement of binary number is obtained by adding 1 to the Least Significant Bit (LSB) of 1's complement of the number.
2's complement = 1's complement + 1
Example of 2's Complement is as follows.
Binary arithmetic is essential part of all the digital computers and many other digital system.
Binary Addition
It is a key for binary subtraction, multiplication, division. There are four rules of binary addition.
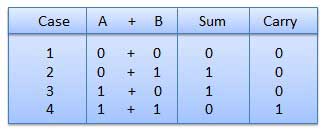
In fourth case, a binary addition is creating a sum of (1 + 1 = 10) i.e. 0 is written in the given column and a carry of 1 over to the next column.
Example − Addition
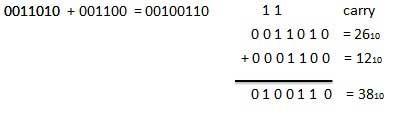
Binary Subtraction
Subtraction and Borrow, these two words will be used very frequently for the binary subtraction. There are four rules of binary subtraction.
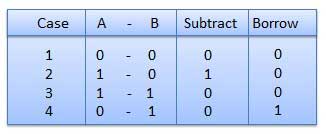
Example − Subtraction
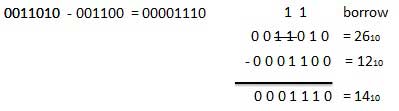
Binary Multiplication
Binary multiplication is similar to decimal multiplication. It is simpler than decimal multiplication because only 0s and 1s are involved. There are four rules of binary multiplication.
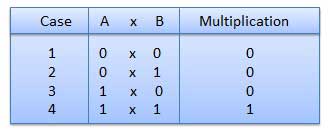
Example − Multiplication

Binary Division
Binary division is similar to decimal division. It is called as the long division procedure.
Example − Division

Octal Number System
Following are the characteristics of an octal number system.
Uses eight digits, 0,1,2,3,4,5,6,7.
Also called base 8 number system.
Each position in an octal number represents a 0 power of the base (8). Example: 80
Last position in an octal number represents an x power of the base (8). Example: 8x where x represents the last position - 1.
Example
Octal Number − 125708
Calculating Decimal Equivalent −
| Step | Octal Number | Decimal Number |
|---|---|---|
| Step 1 | 125708 | ((1 × 84) + (2 × 83) + (5 × 82) + (7 × 81) + (0 × 80))10 |
| Step 2 | 125708 | (4096 + 1024 + 320 + 56 + 0)10 |
| Step 3 | 125708 | 549610 |
Note − 125708 is normally written as 12570.
Octal Addition
Following octal addition table will help you to handle octal addition.

To use this table, simply follow the directions used in this example: Add 68 and 58. Locate 6 in the A column then locate the 5 in the B column. The point in 'sum' area where these two columns intersect is the 'sum' of two numbers.
68 + 58 = 138.Example − Addition
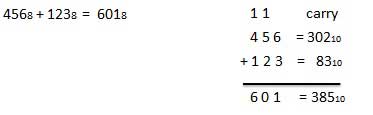
Octal Subtraction
The subtraction of octal numbers follows the same rules as the subtraction of numbers in any other number system. The only variation is in borrowed number. In the decimal system, you borrow a group of 1010. In the binary system, you borrow a group of 210. In the octal system you borrow a group of 810.
Example − Subtraction
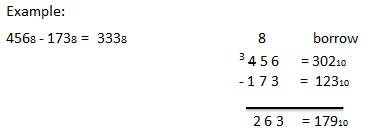
Hexadecimal Number System
Following are the characteristics of a hexadecimal number system.
Uses 10 digits and 6 letters, 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.
Letters represents numbers starting from 10. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Also called base 16 number system.
Each position in a hexadecimal number represents a 0 power of the base (16). Example − 160
Last position in a hexadecimal number represents an x power of the base (16). Example − 16x where x represents the last position - 1.
Example
Hexadecimal Number − 19FDE16
Calculating Decimal Equivalent −
| Step | Hexadecimal Number | Decimal Number |
|---|---|---|
| Step 1 | 19FDE16 | ((1 × 164) + (9 × 163) + (F × 162) + (D × 161) + (E × 160))10 |
| Step 2 | 19FDE16 | ((1 × 164) + (9 × 163) + (15 × 162) + (13 × 161) + (14 × 160))10 |
| Step 3 | 19FDE16 | (65536 + 36864 + 3840 + 208 + 14)10 |
| Step 4 | 19FDE16 | 10646210 |
Note − 19FDE16 is normally written as 19FDE.
Hexadecimal Addition
Following hexadecimal addition table will help you greatly to handle Hexadecimal addition.
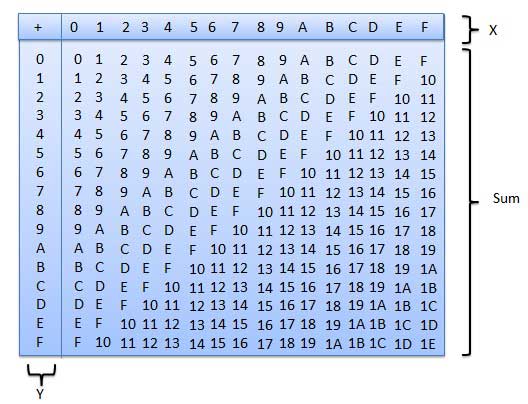
To use this table, simply follow the directions used in this example − Add A16 and 516. Locate A in the X column then locate the 5 in the Y column. The point in 'sum' area where these two columns intersect is the sum of two numbers.
A16 + 516 = F16.Example − Addition
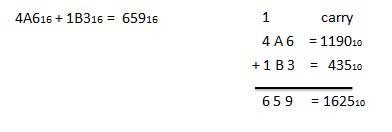
Hexadecimal Subtraction
The subtraction of hexadecimal numbers follow the same rules as the subtraction of numbers in any other number system. The only variation is in borrowed number. In the decimal system, you borrow a group of 1010. In the binary system, you borrow a group of 210. In the hexadecimal system you borrow a group of 1610.
Example - Subtraction

Boolean Algebra is used to analyze and simplify the digital (logic) circuits. It uses only the binary numbers i.e. 0 and 1. It is also called as Binary Algebra or logical Algebra. Boolean algebra was invented by George Boole in 1854.
Rule in Boolean Algebra
Following are the important rules used in Boolean algebra.
Variable used can have only two values. Binary 1 for HIGH and Binary 0 for LOW.
Complement of a variable is represented by an overbar (-). Thus, complement of variable B is represented as
. Thus if B = 0 then = 1 and B = 1 then
= 1 and B = 1 then = 0.
= 0.
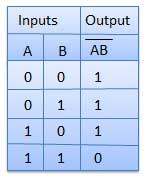
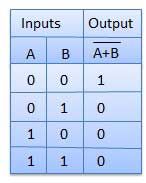
ORing of the variables is represented by a plus (+) sign between them. For example ORing of A, B, C is represented as A + B + C.
Logical ANDing of the two or more variable is represented by writing a dot between them such as A.B.C. Sometime the dot may be omitted like ABC.
Boolean Laws
There are six types of Boolean Laws.
Commutative law
Any binary operation which satisfies the following expression is referred to as commutative operation.

Commutative law states that changing the sequence of the variables does not have any effect on the output of a logic circuit.
Associative law
This law states that the order in which the logic operations are performed is irrelevant as their effect is the same.
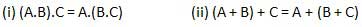
Distributive law
Distributive law states the following condition.
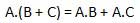
AND law
These laws use the AND operation. Therefore they are called as AND laws.
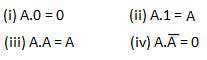
OR law
These laws use the OR operation. Therefore they are called as OR laws.
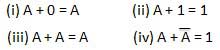
INVERSION law
This law uses the NOT operation. The inversion law states that double inversion of a variable results in the original variable itself.
Important Boolean Theorems
Following are few important boolean Theorems.
| Boolean function/theorems | Description |
|---|---|
Boolean Functions |
Boolean Functions and Expressions, K-Map and NAND Gates realization |
De Morgan's Theorems |
De Morgan's Theorem 1 and Theorem 2 |
Logic gates are the basic building blocks of any digital system. It is an electronic circuit having one or more than one input and only one output. The relationship between the input and the output is based on a certain logic. Based on this, logic gates are named as AND gate, OR gate, NOT gate etc.
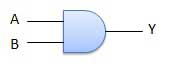
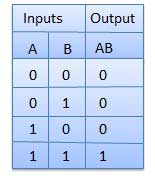
AND Gate
A circuit which performs an AND operation is shown in figure. It has n input (n >= 2) and one output.

Logic diagram
Truth Table
OR Gate
A circuit which performs an OR operation is shown in figure. It has n input (n >= 2) and one output.
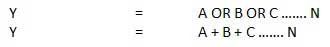
Logic diagram
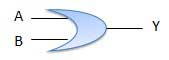
Truth Table
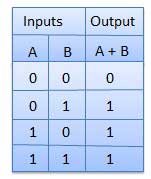
NOT Gate
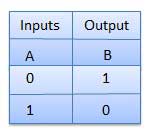
NOT gate is also known as Inverter. It has one input A and one output Y.
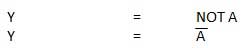
Logic diagram
Truth Table
NAND Gate
A NOT-AND operation is known as NAND operation. It has n input (n >= 2) and one output.
Logic diagram
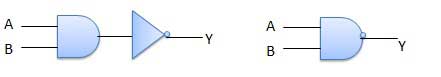
Truth Table
NOR Gate
A NOT-OR operation is known as NOR operation. It has n input (n >= 2) and one output.
Logic diagram
Truth Table
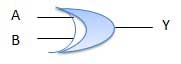
XOR Gate
XOR or Ex-OR gate is a special type of gate. It can be used in the half adder, full adder and subtractor. The exclusive-OR gate is abbreviated as EX-OR gate or sometime as X-OR gate. It has n input (n >= 2) and one output.
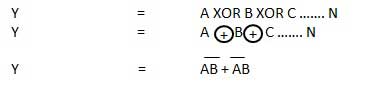
Logic diagram
Truth Table
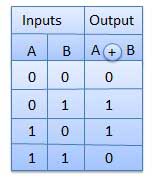
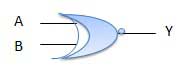
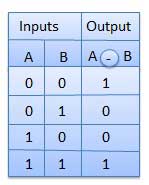
XNOR Gate
XNOR gate is a special type of gate. It can be used in the half adder, full adder and subtractor. The exclusive-NOR gate is abbreviated as EX-NOR gate or sometime as X-NOR gate. It has n input (n >= 2) and one output.
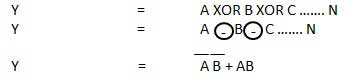
Logic diagram
Truth Table
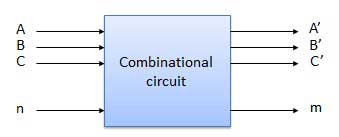
Combinational circuit is a circuit in which we combine the different gates in the circuit, for example encoder, decoder, multiplexer and demultiplexer. Some of the characteristics of combinational circuits are following −
The output of combinational circuit at any instant of time, depends only on the levels present at input terminals.
The combinational circuit do not use any memory. The previous state of input does not have any effect on the present state of the circuit.
A combinational circuit can have an n number of inputs and m number of outputs.
Block diagram
We're going to elaborate few important combinational circuits as follows.
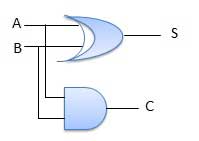
Half Adder
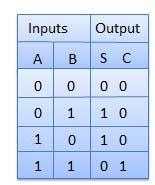
Half adder is a combinational logic circuit with two inputs and two outputs. The half adder circuit is designed to add two single bit binary number A and B. It is the basic building block for addition of two single bit numbers. This circuit has two outputs carry and sum.
Block diagram

Truth Table
Circuit Diagram
Full Adder
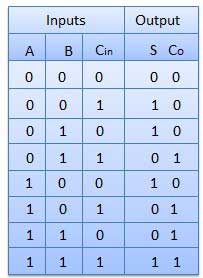
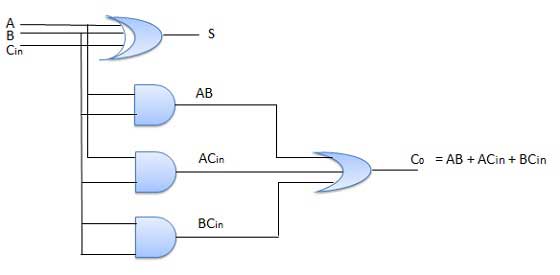
Full adder is developed to overcome the drawback of Half Adder circuit. It can add two one-bit numbers A and B, and carry c. The full adder is a three input and two output combinational circuit.
Block diagram

Truth Table
Circuit Diagram
N-Bit Parallel Adder
The Full Adder is capable of adding only two single digit binary number along with a carry input. But in practical we need to add binary numbers which are much longer than just one bit. To add two n-bit binary numbers we need to use the n-bit parallel adder. It uses a number of full adders in cascade. The carry output of the previous full adder is connected to carry input of the next full adder.
4 Bit Parallel Adder
In the block diagram, A0 and B0 represent the LSB of the four bit words A and B. Hence Full Adder-0 is the lowest stage. Hence its Cin has been permanently made 0. The rest of the connections are exactly same as those of n-bit parallel adder is shown in fig. The four bit parallel adder is a very common logic circuit.
Block diagram

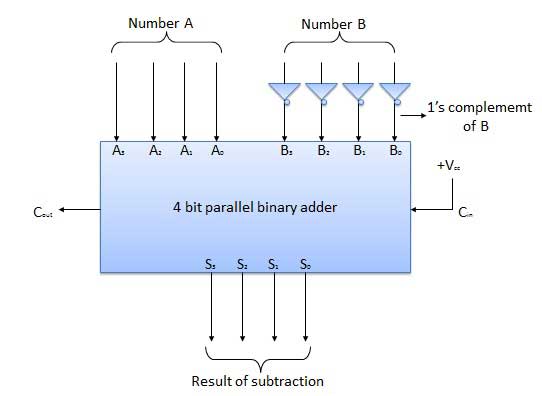
N-Bit Parallel Subtractor
The subtraction can be carried out by taking the 1's or 2's complement of the number to be subtracted. For example we can perform the subtraction (A-B) by adding either 1's or 2's complement of B to A. That means we can use a binary adder to perform the binary subtraction.
4 Bit Parallel Subtractor
The number to be subtracted (B) is first passed through inverters to obtain its 1's complement. The 4-bit adder then adds A and 2's complement of B to produce the subtraction. S3 S2 S1 S0 represents the result of binary subtraction (A-B) and carry output Cout represents the polarity of the result. If A > B then Cout = 0 and the result of binary form (A-B) then Cout = 1 and the result is in the 2's complement form.
Block diagram
Half Subtractors
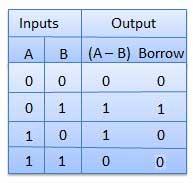
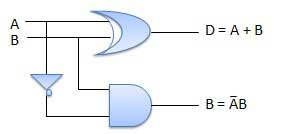
Half subtractor is a combination circuit with two inputs and two outputs (difference and borrow). It produces the difference between the two binary bits at the input and also produces an output (Borrow) to indicate if a 1 has been borrowed. In the subtraction (A-B), A is called as Minuend bit and B is called as Subtrahend bit.
Truth Table
Circuit Diagram
Full Subtractors
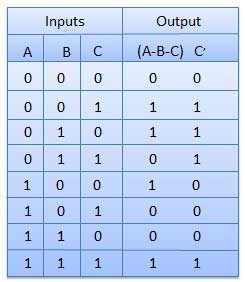
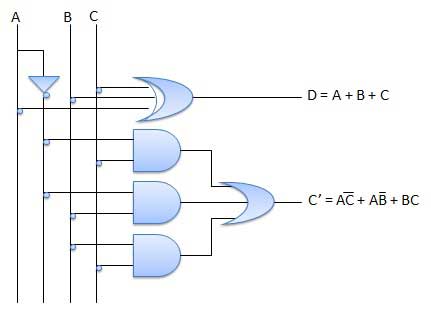
The disadvantage of a half subtractor is overcome by full subtractor. The full subtractor is a combinational circuit with three inputs A,B,C and two output D and C'. A is the 'minuend', B is 'subtrahend', C is the 'borrow' produced by the previous stage, D is the difference output and C' is the borrow output.
Truth Table
Circuit Diagram
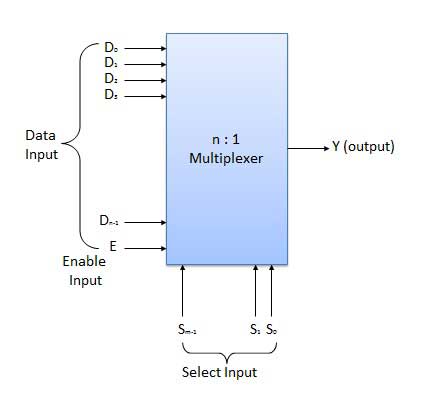
Multiplexers
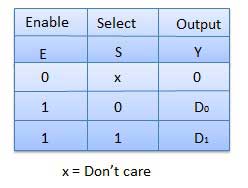
Multiplexer is a special type of combinational circuit. There are n-data inputs, one output and m select inputs with 2m = n. It is a digital circuit which selects one of the n data inputs and routes it to the output. The selection of one of the n inputs is done by the selected inputs. Depending on the digital code applied at the selected inputs, one out of n data sources is selected and transmitted to the single output Y. E is called the strobe or enable input which is useful for the cascading. It is generally an active low terminal that means it will perform the required operation when it is low.
Block diagram
Multiplexers come in multiple variations
- 2 : 1 multiplexer
- 4 : 1 multiplexer
- 16 : 1 multiplexer
- 32 : 1 multiplexer
Block Diagram
Truth Table
Demultiplexers
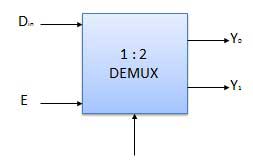
A demultiplexer performs the reverse operation of a multiplexer i.e. it receives one input and distributes it over several outputs. It has only one input, n outputs, m select input. At a time only one output line is selected by the select lines and the input is transmitted to the selected output line. A de-multiplexer is equivalent to a single pole multiple way switch as shown in fig.
Demultiplexers comes in multiple variations.
- 1 : 2 demultiplexer
- 1 : 4 demultiplexer
- 1 : 16 demultiplexer
- 1 : 32 demultiplexer
Block diagram
Truth Table
Decoder
A decoder is a combinational circuit. It has n input and to a maximum m = 2n outputs. Decoder is identical to a demultiplexer without any data input. It performs operations which are exactly opposite to those of an encoder.
Block diagram

Examples of Decoders are following.
- Code converters
- BCD to seven segment decoders
- Nixie tube decoders
- Relay actuator
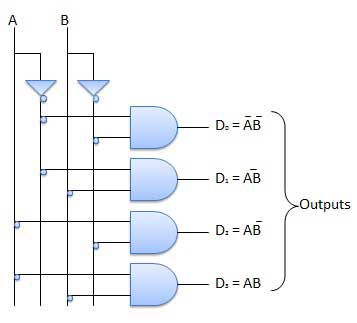
2 to 4 Line Decoder
The block diagram of 2 to 4 line decoder is shown in the fig. A and B are the two inputs where D through D are the four outputs. Truth table explains the operations of a decoder. It shows that each output is 1 for only a specific combination of inputs.
Block diagram

Truth Table

Logic Circuit
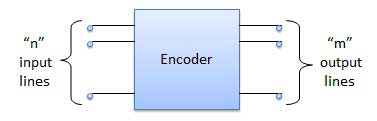
Encoder
Encoder is a combinational circuit which is designed to perform the inverse operation of the decoder. An encoder has n number of input lines and m number of output lines. An encoder produces an m bit binary code corresponding to the digital input number. The encoder accepts an n input digital word and converts it into an m bit another digital word.
Block diagram
Examples of Encoders are following.
- Priority encoders
- Decimal to BCD encoder
- Octal to binary encoder
- Hexadecimal to binary encoder
Priority Encoder
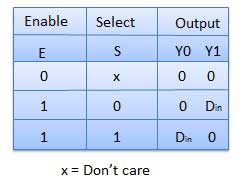
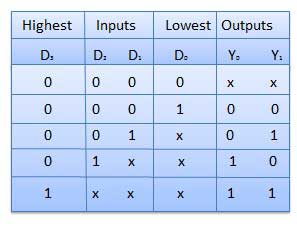
This is a special type of encoder. Priority is given to the input lines. If two or more input line are 1 at the same time, then the input line with highest priority will be considered. There are four input D0, D1, D2, D3 and two output Y0, Y1. Out of the four input D3 has the highest priority and D0 has the lowest priority. That means if D3 = 1 then Y1 Y1 = 11 irrespective of the other inputs. Similarly if D3 = 0 and D2 = 1 then Y1 Y0 = 10 irrespective of the other inputs.
Block diagram

Truth Table
Logic Circuit
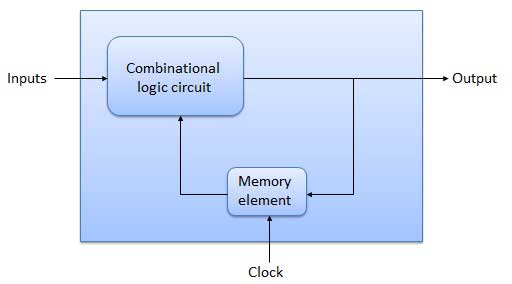
The combinational circuit does not use any memory. Hence the previous state of input does not have any effect on the present state of the circuit. But sequential circuit has memory so output can vary based on input. This type of circuits uses previous input, output, clock and a memory element.
Block diagram
Flip Flop
Flip flop is a sequential circuit which generally samples its inputs and changes its outputs only at particular instants of time and not continuously. Flip flop is said to be edge sensitive or edge triggered rather than being level triggered like latches.
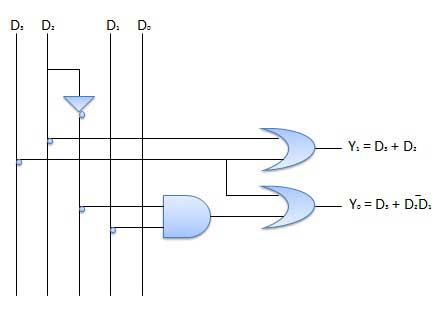
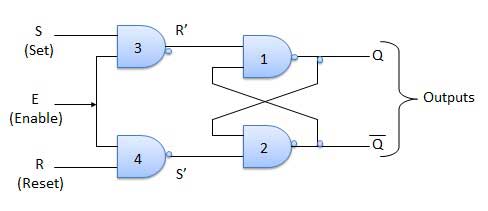
S-R Flip Flop
It is basically S-R latch using NAND gates with an additional enable input. It is also called as level triggered SR-FF. For this, circuit in output will take place if and only if the enable input (E) is made active. In short this circuit will operate as an S-R latch if E = 1 but there is no change in the output if E = 0.
Block Diagram
Circuit Diagram
Truth Table
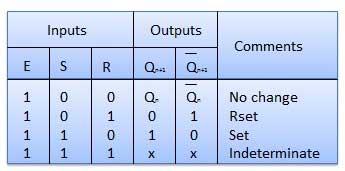
Operation
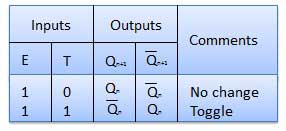
| S.N. | Condition | Operation |
|---|---|---|
| 1 | S = R = 0 : No change | If S = R = 0 then output of NAND gates 3 and 4 are forced to become 1. Hence R' and S' both will be equal to 1. Since S' and R' are the input of the basic S-R latch using NAND gates, there will be no change in the state of outputs. |
| 2 | S = 0, R = 1, E = 1 | Since S = 0, output of NAND-3 i.e. R' = 1 and E = 1 the output of NAND-4 i.e. S' = 0. Hence Qn+1 = 0 and Qn+1 bar = 1. This is reset condition. |
| 3 | S = 1, R = 0, E = 1 | Output of NAND-3 i.e. R' = 0 and output of NAND-4 i.e. S' = 1. Hence output of S-R NAND latch is Qn+1 = 1 and Qn+1 bar = 0. This is the reset condition. |
| 4 | S = 1, R = 1, E = 1 | As S = 1, R = 1 and E = 1, the output of NAND gates 3 and 4 both are 0 i.e. S' = R' = 0. Hence the Race condition will occur in the basic NAND latch. |
Master Slave JK Flip Flop
Master slave JK FF is a cascade of two S-R FF with feedback from the output of second to input of first. Master is a positive level triggered. But due to the presence of the inverter in the clock line, the slave will respond to the negative level. Hence when the clock = 1 (positive level) the master is active and the slave is inactive. Whereas when clock = 0 (low level) the slave is active and master is inactive.
Circuit Diagram
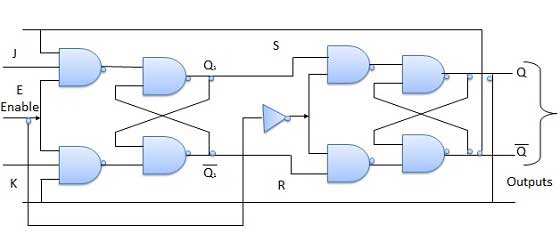
Truth Table
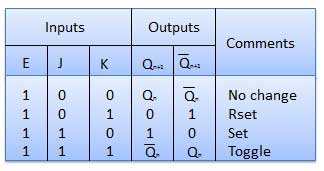
Operation
| S.N. | Condition | Operation |
|---|---|---|
| 1 | J = K = 0 (No change) | When clock = 0, the slave becomes active and master is inactive. But since the S and R inputs have not changed, the slave outputs will also remain unchanged. Therefore outputs will not change if J = K =0. |
| 2 | J = 0 and K = 1 (Reset) | Clock = 1 − Master active, slave inactive. Therefore outputs of the master become Q1 = 0 and Q1 bar = 1. That means S = 0 and R =1. Clock = 0 − Slave active, master inactive. Therefore outputs of the slave become Q = 0 and Q bar = 1. Again clock = 1 − Master active, slave inactive. Therefore even with the changed outputs Q = 0 and Q bar = 1 fed back to master, its output will be Q1 = 0 and Q1 bar = 1. That means S = 0 and R = 1. Hence with clock = 0 and slave becoming active the outputs of slave will remain Q = 0 and Q bar = 1. Thus we get a stable output from the Master slave. |
| 3 | J = 1 and K = 0 (Set) | Clock = 1 − Master active, slave inactive. Therefore outputs of the master become Q1 = 1 and Q1 bar = 0. That means S = 1 and R =0. Clock = 0 − Slave active, master inactive. Therefore outputs of the slave become Q = 1 and Q bar = 0. Again clock = 1 − then it can be shown that the outputs of the slave are stabilized to Q = 1 and Q bar = 0. |
| 4 | J = K = 1 (Toggle) | Clock = 1 − Master active, slave inactive. Outputs of master will toggle. So S and R also will be inverted. Clock = 0 − Slave active, master inactive. Outputs of slave will toggle. These changed output are returned back to the master inputs. But since clock = 0, the master is still inactive. So it does not respond to these changed outputs. This avoids the multiple toggling which leads to the race around condition. The master slave flip flop will avoid the race around condition. |
Delay Flip Flop / D Flip Flop
Delay Flip Flop or D Flip Flop is the simple gated S-R latch with a NAND inverter connected between S and R inputs. It has only one input. The input data is appearing at the output after some time. Due to this data delay between i/p and o/p, it is called delay flip flop. S and R will be the complements of each other due to NAND inverter. Hence S = R = 0 or S = R = 1, these input condition will never appear. This problem is avoid by SR = 00 and SR = 1 conditions.
Block Diagram
Circuit Diagram
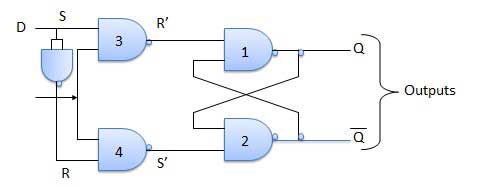
Truth Table
Operation
| S.N. | Condition | Operation |
|---|---|---|
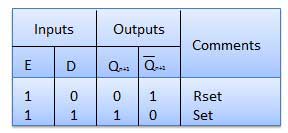
| 1 | E = 0 | Latch is disabled. Hence no change in output. |
| 2 | E = 1 and D = 0 | If E = 1 and D = 0 then S = 0 and R = 1. Hence irrespective of the present state, the next state is Qn+1 = 0 and Qn+1 bar = 1. This is the reset condition. |
| 3 | E = 1 and D = 1 | If E = 1 and D = 1, then S = 1 and R = 0. This will set the latch and Qn+1 = 1 and Qn+1 bar = 0 irrespective of the present state. |
Toggle Flip Flop / T Flip Flop
Toggle flip flop is basically a JK flip flop with J and K terminals permanently connected together. It has only input denoted by T as shown in the Symbol Diagram. The symbol for positive edge triggered T flip flop is shown in the Block Diagram.
Symbol Diagram
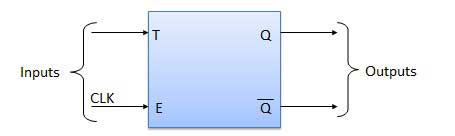
Block Diagram
Truth Table
Operation
| S.N. | Condition | Operation |
|---|---|---|
| 1 | T = 0, J = K = 0 | The output Q and Q bar won't change |
| 2 | T = 1, J = K = 1 | Output will toggle corresponding to every leading edge of clock signal. |
Flip-flop is a 1 bit memory cell which can be used for storing the digital data. To increase the storage capacity in terms of number of bits, we have to use a group of flip-flop. Such a group of flip-flop is known as a Register. The n-bit register will consist of n number of flip-flop and it is capable of storing an n-bit word.
The binary data in a register can be moved within the register from one flip-flop to another. The registers that allow such data transfers are called as shift registers. There are four mode of operations of a shift register.
- 직렬 입력 직렬 출력
- 직렬 입력 병렬 출력
- 병렬 입력 직렬 출력
- 병렬 입력 병렬 출력
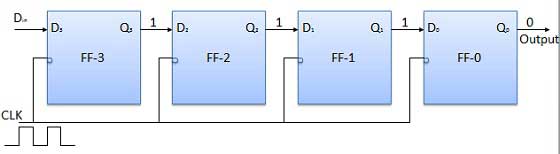
직렬 입력 직렬 출력
모든 플립 플롭이 초기에 리셋 상태에 있도록합니다. 즉 Q 3 = Q 2 = Q 1 = Q 0 = 0입니다. 레지스터에 4 비트 이진 숫자 1 1 1 1이 입력되면이 숫자는 다음과 같아야합니다. 적용DinLSB 비트가 먼저 적용된 비트. FF-3 즉 D 3 의 D 입력은 직렬 데이터 입력에 연결됩니다.Din. FF-3, 즉 Q 3 의 출력은 다음 플립 플롭, 즉 D 2 의 입력에 연결됩니다 .
블록 다이어그램
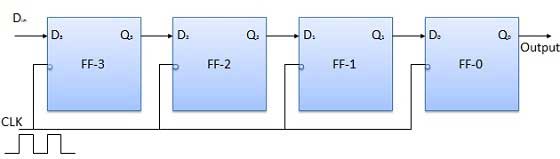
조작
클럭 신호를 적용하기 전에 Q 3 Q 2 Q 1 Q 0 = 0000으로하고 입력 할 숫자의 LSB 비트 를 . 따라서 D in = D 3 = 1. 시계를 적용합니다. 클록의 첫 번째 하강 에지에서 FF-3이 설정되고 레지스터에 저장된 워드는 Q 3 Q 2 Q 1 Q 0 = 1000입니다.
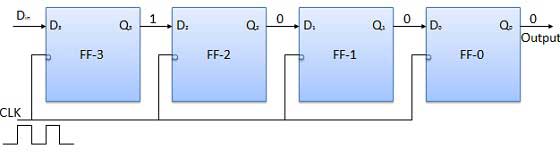
에서 D 에 다음 비트를 적용합니다 . 따라서 D in = 1입니다. 클럭의 다음 음의 에지에 도달하면 FF-2가 설정되고 저장된 워드가 Q 3 Q 2 Q 1 Q 0 = 1100으로 변경됩니다.
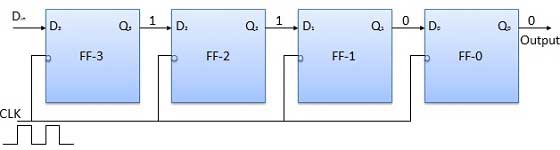
저장 될 다음 비트를 적용합니다 . 즉 1에서 D in . 클럭 펄스를 적용합니다. 세 번째 네거티브 클록 에지에 도달하자마자 FF-1이 설정되고 출력이 Q 3 Q 2 Q 1 Q 0 = 1110 으로 수정됩니다 .
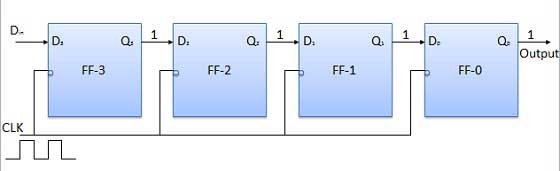
마찬가지로 D in = 1이고 네 번째 음의 클록 에지가 도착하면 레지스터에 저장된 워드는 Q 3 Q 2 Q 1 Q 0 = 1111입니다.
진실 테이블
파형

직렬 입력 병렬 출력
이러한 유형의 작업에서 데이터는 직렬로 입력되고 병렬 방식으로 추출됩니다.
데이터는 비트 단위로로드됩니다. 데이터가로드되는 동안에는 출력이 비활성화됩니다.
데이터 로딩이 완료 되 자마자 모든 플립 플롭에 필요한 데이터가 포함되고 출력이 활성화되어로드 된 모든 데이터를 모든 출력 라인에서 동시에 사용할 수 있습니다.
4 비트 워드를로드하려면 4 클럭 사이클이 필요합니다. 따라서 SIPO 모드의 작동 속도는 SISO 모드의 속도와 동일합니다.
블록 다이어그램
병렬 입력 직렬 출력 (PISO)
데이터 비트는 병렬 방식으로 입력됩니다.
아래에 표시된 회로는 4 비트 병렬 입력 직렬 출력 레지스터입니다.
이전 플립 플롭의 출력은 조합 회로를 통해 다음 플립 플롭의 입력에 연결됩니다.
바이너리 입력 워드 B 0 , B 1 , B 2 , B 3 은 동일한 조합 회로를 통해 적용됩니다.
이 회로가 작동 할 수있는 두 가지 모드, 즉 시프트 모드 또는로드 모드가 있습니다.
로드 모드
시프트 /로드 바 라인이 낮 으면 (0) AND 게이트 2, 4 및 6이 활성화되어 B 1 , B 2 , B 3 비트를 해당 플립 플롭에 전달합니다. 클럭의 낮은 에지에서 이진 입력 B 0 , B 1 , B 2 , B 3 은 해당 플립 플롭에로드됩니다. 따라서 병렬 로딩이 발생합니다.
시프트 모드
변속 / 부하 막대 라인이 낮 으면 (1) AND 게이트 2, 4 및 6이 비활성화됩니다. 따라서 데이터의 병렬로드가 불가능합니다. 그러나 AND 게이트 1,3 및 5가 활성화됩니다. 따라서 클럭 펄스를 적용 할 때 데이터가 왼쪽에서 오른쪽으로 조금씩 이동합니다. 따라서 직렬 출력 작업에서 병렬이 발생합니다.
블록 다이어그램
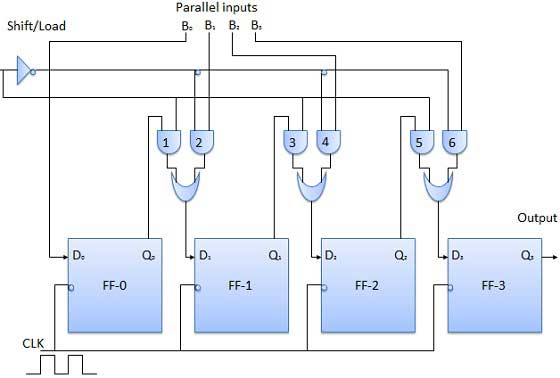
병렬 입력 병렬 출력 (PIPO)
이 모드에서 4 비트 이진 입력 B 0 , B 1 , B 2 , B 3 은 4 개의 플립 플롭 의 데이터 입력 D 0 , D 1 , D 2 , D 3 각각에 적용됩니다. 네거티브 클럭 에지가 적용되 자마자 입력 이진 비트가 플립 플롭에 동시에로드됩니다. 로드 된 비트는 출력 측에 동시에 나타납니다. 모든 비트를로드하려면 클럭 펄스 만 필요합니다.
블록 다이어그램
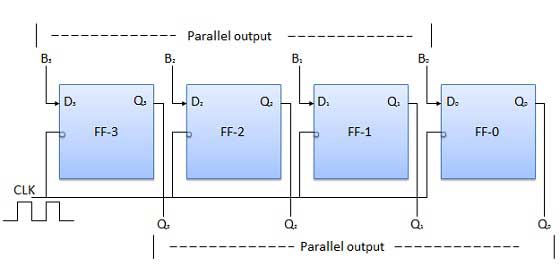
양방향 시프트 레지스터
이진수가 한 자리 왼쪽으로 이동하면 원래 숫자에 2를 곱하는 것과 같습니다. 마찬가지로 이진수가 오른쪽으로 한 자리 이동하면 원래 숫자를 2로 나눈 것과 같습니다.
따라서 주어진 이진수를 곱하고 나누기 위해 시프트 레지스터를 사용하려면 데이터를 왼쪽 또는 오른쪽 방향으로 이동할 수 있어야합니다.
이러한 레지스터를 양방향 레지스터라고합니다. 4 비트 양방향 시프트 레지스터가 그림에 나와 있습니다.
직렬 오른쪽 시프트 데이터 입력 DR과 모드 선택 입력 (M)과 함께 직렬 왼쪽 시프트 데이터 입력 DL의 두 개의 직렬 입력이 있습니다.
블록 다이어그램
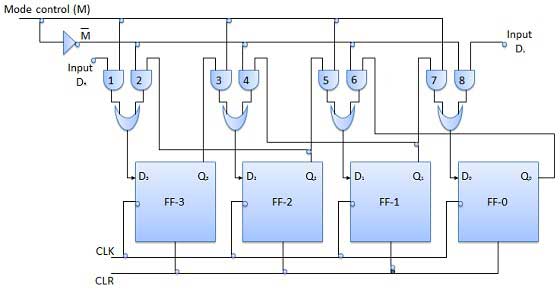
조작
| SN | 질환 | 조작 |
|---|---|---|
| 1 | With M = 1 − Shift right operation | M = 1이면 AND 게이트 1, 3, 5 및 7이 활성화되고 나머지 AND 게이트 2, 4, 6 및 8은 비활성화됩니다. D R 의 데이터 는 클럭 펄스를 적용 할 때 FF-3에서 FF-0으로 비트 단위로 오른쪽으로 이동합니다. 따라서 M = 1이면 직렬 오른쪽 시프트 연산이 수행됩니다. |
| 2 | With M = 0 − Shift left operation | 모드 제어 M이 0에 연결되면 AND 게이트 2, 4, 6 및 8이 활성화되고 1, 3, 5 및 7은 비활성화됩니다. D L 의 데이터 는 클럭 펄스를 적용 할 때 FF-0에서 FF-3으로 비트 씩 왼쪽으로 이동합니다. 따라서 M = 0으로 직렬 오른쪽 시프트 연산을 얻습니다. |
범용 시프트 레지스터
데이터를 한 방향으로 만 시프트 할 수있는 시프트 레지스터를 단방향 시프트 레지스터라고합니다. 양방향으로 데이터를 이동할 수있는 시프트 레지스터를 양방향 시프트 레지스터라고합니다. 동일한 논리를 적용하여 데이터를 양방향으로 이동하고 병렬로로드 할 수있는 시프트 레지스터를 범용 시프트 레지스터라고합니다. 시프트 레지스터는 다음 작업을 수행 할 수 있습니다.
- 병렬 로딩
- 왼쪽 이동
- 오른쪽 이동
모드 제어 입력은 병렬 로딩 작동을 위해 로직 1에 연결되고 직렬 시프 팅을 위해 0에 연결됩니다. 모드 제어 핀이 접지에 연결된 상태에서 범용 시프트 레지스터는 양방향 레지스터로 작동합니다. 직렬 왼쪽 작업의 경우 입력은 그림과 같이 AND gate-1로가는 직렬 입력에 적용됩니다. 오른쪽 시프트 작업의 경우 직렬 입력이 D 입력에 적용됩니다.
블록 다이어그램
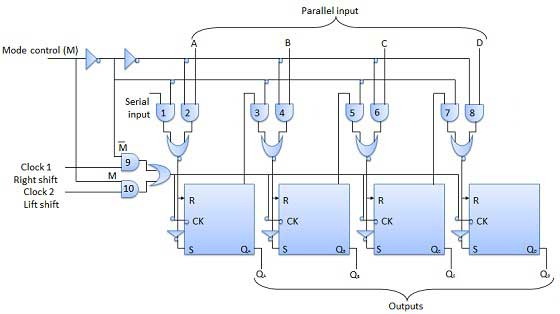
카운터는 순차 회로입니다. 카운트 펄스에 사용되는 디지털 회로는 알려진 카운터입니다. 카운터는 플립 플롭의 가장 광범위한 응용 프로그램입니다. 클럭 신호가 적용된 플립 플롭 그룹입니다. 카운터는 두 가지 유형이 있습니다.
- 비동기 또는 리플 카운터.
- 동기식 카운터.
비동기 또는 리플 카운터
2 비트 리플 업 카운터의 논리 다이어그램이 그림에 나와 있습니다. 토글 (T) 플립 플롭이 사용되고 있습니다. 그러나 J와 K가 로직 1에 영구적으로 연결된 상태에서도 JK 플립 플롭을 사용할 수 있습니다. 외부 클럭은 플립 플롭 A 의 클럭 입력에 적용 되고 Q A 출력은 다음 플립 플롭의 클럭 입력에 적용됩니다. FF-B.
논리 다이어그램
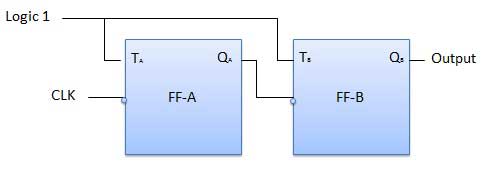
조작
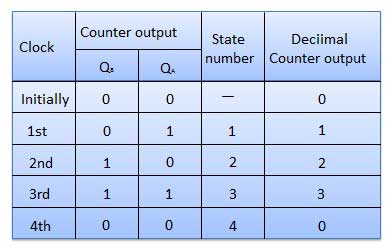
| SN | 질환 | 조작 |
|---|---|---|
| 1 | Initially let both the FFs be in the reset state | Q B Q A = 처음에는 00 |
| 2 | After 1st negative clock edge | 첫 번째 네거티브 클럭 에지가 적용되 자마자 FF-A가 토글되고 Q A 는 1이됩니다. Q A 는 FF-B의 클럭 입력에 연결됩니다. Q A 가 0에서 1로 변경되었으므로 FF-B에 의해 양의 클럭 에지로 처리됩니다. FF-B는 네거티브 에지 트리거 FF이기 때문에 Q B 에는 변화가 없습니다 . Q B Q A = 첫 번째 클록 펄스 이후 01. |
| 삼 | After 2nd negative clock edge | 두 번째 네거티브 클럭 에지에 도달하면 FF-A가 다시 토글되고 Q A = 0입니다. Q A 의 변화는 FF-B의 음의 클록 에지 역할을합니다. 따라서 또한 토글되고 Q B 는 1이됩니다. Q B Q A = 두 번째 클럭 펄스 이후 10. |
| 4 | After 3rd negative clock edge | 세 번째 음의 클럭 에지가 도착하면 FF-A가 다시 토글되고 Q A 는 0에서 1이됩니다. 이것은 긍정적 인 변화이기 때문에 FF-B는 이에 응답하지 않고 비활성 상태로 유지됩니다. 따라서 Q B 는 변하지 않고 계속 1과 같습니다. Q B Q A = 11 번째 클럭 펄스 이후. |
| 5 | After 4th negative clock edge | 네 번째 네거티브 클럭 에지에 도달하면 FF-A가 다시 토글되고 Q A 는 0에서 1이됩니다. Q A의 이러한 음의 변화는 FF-B의 클럭 펄스 역할을합니다. 따라서 Q B 를 1에서 0 으로 변경하도록 전환됩니다 . Q B Q A = 네 번째 클록 펄스 이후 00. |
진실 테이블
동기식 카운터
"클록"펄스가 카운터의 모든 플립 플롭에 동시에 적용되는 경우 이러한 카운터를 동기식 카운터라고합니다.
2 비트 동기식 업 카운터
FF-A 의 J A 및 K A 입력은 논리 1에 연결됩니다. 따라서 FF-A는 토글 플립 플롭으로 작동합니다. J B 및 K B 입력은 Q A에 연결됩니다 .
논리 다이어그램

조작
| SN | 질환 | 조작 |
|---|---|---|
| 1 | Initially let both the FFs be in the reset state | Q B Q A = 처음에는 00. |
| 2 | After 1st negative clock edge | 첫 번째 네거티브 클럭 에지가 적용되 자마자 FF-A가 토글되고 Q A 가 0에서 1로 변경됩니다. 그러나 네거티브 클럭 에지를 적용하는 순간 Q A , J B = K B = 0. 따라서 FF-B는 상태를 변경하지 않습니다. 따라서 Q B 는 0으로 유지됩니다. Q B Q A = 첫 번째 클록 펄스 이후 01. |
| 삼 | After 2nd negative clock edge | 두 번째 네거티브 클럭 에지에 도달하면 FF-A가 다시 토글되고 Q A 가 1에서 0으로 변경됩니다. 그러나이 순간 Q A 는 1이었습니다. 따라서 J B = K B = 1이고 FF-B가 전환됩니다. 따라서 Q B 는 0에서 1로 변경됩니다. Q B Q A = 두 번째 클럭 펄스 이후 10. |
| 4 | After 3rd negative clock edge | 세 번째 하강 클럭 에지를 적용하면 FF-A가 0에서 1로 전환되지만 FF-B에 대한 상태 변경은 없습니다. Q B Q A = 11 번째 클럭 펄스 이후. |
| 5 | After 4th negative clock edge | 다음 클럭 펄스 를 적용하면 Q B 도 1에서 0으로 변경되므로 Q A 는 1에서 0으로 변경됩니다. Q B Q A = 네 번째 클록 펄스 이후 00. |
카운터 분류
계산이 진행되는 방식에 따라 동기식 또는 비동기식 카운터는 다음과 같이 분류됩니다.
- 업 카운터
- 다운 카운터
- 업 / 다운 카운터
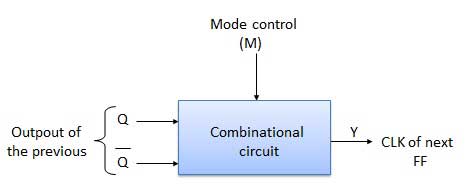
UP / DOWN 카운터
업 카운터와 다운 카운터를 결합하여 UP / DOWN 카운터를 얻습니다. 모드 제어 (M) 입력도 제공되어 업 또는 다운 모드를 선택합니다. 업 / 다운 작동을 위해서는 각 플립 플롭 쌍 사이에 조합 회로를 설계하고 사용해야합니다.
- 업 / 다운 카운터 유형
- 위 / 아래 리플 카운터
- UP / DOWN 동기 카운터
위 / 아래 리플 카운터
UP / DOWN 리플 카운터에서 모든 FF는 토글 모드에서 작동합니다. 따라서 T 플립 플롭 또는 JK 플립 플롭이 사용됩니다. LSB 플립 플롭은 클럭을 직접 수신합니다. 그러나 다른 모든 FF에 대한 클럭은 이전 FF의 (Q = Q bar) 출력에서 얻습니다.
UP counting mode (M=0)− 업 카운팅을 달성하려면 선행 FF의 Q 출력이 다음 단계의 클록에 연결됩니다. 이 모드의 경우 모드 선택 입력 M은 논리 0 (M = 0)에 있습니다.
DOWN counting mode (M=1)− M = 1이면 이전 FF의 Q bar 출력이 다음 FF에 연결됩니다. 이것은 계수 모드에서 카운터를 작동합니다.
예
3 비트 바이너리 업 / 다운 리플 카운터.
3 비트-따라서 3 개의 FF가 필요합니다.
UP / DOWN-따라서 모드 제어 입력이 필수적입니다.
리플 업 카운터의 경우 이전 FF의 Q 출력은 다음 FF의 클록 입력에 연결됩니다.
리플 업 카운터의 경우 이전 FF의 Q 출력은 다음 FF의 클록 입력에 연결됩니다.
리플 다운 카운터의 경우 이전 FF의 Q 바 출력은 다음 FF의 클록 입력에 연결됩니다.
이전 FF의 Q 및 Q bar 출력 선택이 모드 제어 입력 M에 의해 제어되어 M = 0이면 UP 카운팅이됩니다. 따라서 Q를 CLK에 연결하십시오. M = 1이면 DOWN 카운팅. 따라서 Q bar를 CLK에 연결하십시오.
블록 다이어그램
진실 테이블
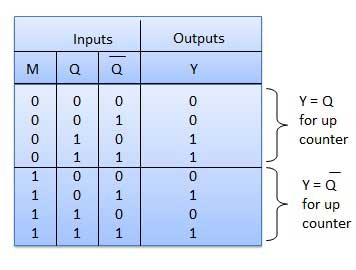
조작
| SN | 질환 | 조작 |
|---|---|---|
| 1 | Case 1 − With M = 0 (Up counting mode) | M = 0이고 M bar = 1이면 그림의 AND 게이트 1과 3입니다. AND 게이트 2와 4는 비활성화됩니다. 따라서 Q A 는 FF-B 의 클록 입력에 연결 되고 Q B 는 FF-C의 클록 입력에 연결됩니다. 이러한 연결은 일반 업 카운터의 연결과 동일합니다. 따라서 M = 0이면 회로가 업 카운터로 작동합니다. |
| 2 | Case 2: With M = 1 (Down counting mode) | M = 1이면 그림의 AND 게이트 2와 4. AND 게이트 1과 3은 비활성화되어 있습니다. 따라서 Q A 바는 FF-B 의 클럭 입력에 연결 되고 Q B 바는 FF-C의 클럭 입력에 연결됩니다. 이러한 연결은 다운 카운터를 생성합니다. 따라서 M = 1이면 회로가 다운 카운터로 작동합니다. |
모듈러스 카운터 (MOD-N 카운터)
2 비트 리플 카운터를 MOD-4 카운터라고하고 3 비트 리플 카운터를 MOD-8 카운터라고합니다. 따라서 일반적으로 n 비트 리플 카운터를 모듈로 N 카운터라고합니다. 여기서 MOD 번호 = 2n .
계수 유형
- 2 비트 업 또는 다운 (MOD-4)
- 3 비트 위로 또는 아래로 (MOD-8)
- 4 비트 업 또는 다운 (MOD-16)
카운터 적용
- 주파수 카운터
- 디지털 시계
- 시간 측정
- A to D 변환기
- 주파수 분배기 회로
- 디지털 삼각파 발생기.
기억은 인간의 뇌와 같습니다. 데이터 및 명령어를 저장하는 데 사용됩니다. 컴퓨터 메모리는 데이터가 처리되고 처리에 필요한 명령이 저장되는 컴퓨터의 저장 공간입니다.
메모리는 많은 수의 작은 부분으로 나뉩니다. 각 부분을 셀이라고합니다. 각 위치 또는 셀에는 0에서 메모리 크기에서 1을 뺀 고유 주소가 있습니다.
예를 들어 컴퓨터에 64k 단어가있는 경우이 메모리 장치에는 64 * 1024 = 65536 메모리 위치가 있습니다. 이러한 위치의 주소는 0에서 65535까지 다양합니다.
메모리는 주로 두 가지 유형입니다.
Internal Memory − 캐시 메모리 및 기본 / 메인 메모리
External Memory − 자기 디스크 / 광 디스크 등
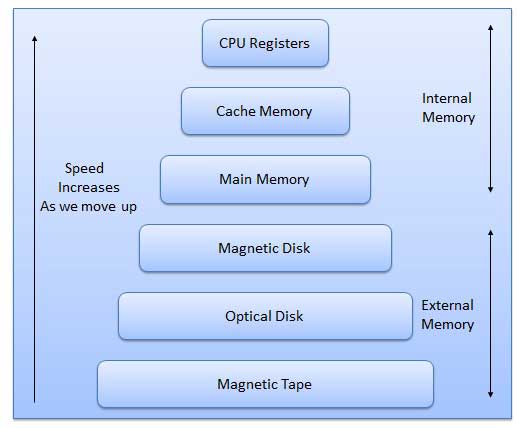
메모리 계층 구조의 특성은 위에서 아래로 이동할 때 따릅니다.
- 스토리지 측면에서 용량이 증가합니다.
- 스토리지 비트 당 비용이 감소합니다.
- CPU에 의한 메모리 액세스 빈도가 감소합니다.
- CPU에 의한 액세스 시간이 증가합니다.
램
RAM은 데이터, 프로그램 및 프로그램 결과를 저장하기위한 CPU의 내부 메모리를 구성합니다. 읽기 / 쓰기 메모리입니다. RAM (Random Access Memory)이라고합니다.
RAM의 액세스 시간은 단어에 대한 주소와 무관하기 때문에 메모리 내부의 각 저장 위치는 다른 위치만큼 쉽게 접근 할 수 있으며 동일한 시간이 걸립니다. 무작위로 매우 빠르게 메모리에 도달 할 수 있지만 비용이 많이들 수도 있습니다.
RAM은 휘발성입니다. 즉, 컴퓨터를 끄거나 정전이 발생하면 저장된 데이터가 손실됩니다. 따라서 백업 무정전 전원 시스템 (UPS)은 종종 컴퓨터와 함께 사용됩니다. RAM은 물리적 크기와 보유 할 수있는 데이터 양면에서 모두 작습니다.
RAM은 두 가지 유형입니다.
- 정적 RAM (SRAM)
- 동적 RAM (DRAM)
정적 RAM (SRAM)
단어 static전원이 공급되는 동안 메모리가 내용을 유지함을 나타냅니다. 그러나 휘발성으로 인해 전원이 꺼지면 데이터가 손실됩니다. SRAM 칩은 6 트랜지스터 매트릭스를 사용하고 커패시터는 사용하지 않습니다. 트랜지스터는 누설을 방지하기 위해 전력이 필요하지 않으므로 SRAM을 정기적으로 새로 고칠 필요가 없습니다.
매트릭스의 추가 공간으로 인해 SRAM은 동일한 양의 저장 공간에 DRAM보다 더 많은 칩을 사용하므로 제조 비용이 높아집니다.
정적 RAM은 캐시 메모리가 매우 빠르고 작아야하기 때문에 사용됩니다.
동적 RAM (DRAM)
SRAM과 달리 DRAM은 지속적으로 refreshed데이터를 유지하기 위해. 이것은 초당 수백 번 데이터를 다시 쓰는 리프레시 회로에 메모리를 배치하여 수행됩니다. DRAM은 저렴하고 작기 때문에 대부분의 시스템 메모리에 사용됩니다. 모든 DRAM은 메모리 셀로 구성됩니다. 이 셀은 하나의 커패시터와 하나의 트랜지스터로 구성됩니다.
ROM
ROM은 읽기 전용 메모리를 의미합니다. 우리가 읽을 수는 있지만 쓸 수는없는 메모리. 이 유형의 메모리는 비 휘발성입니다. 정보는 제조 과정에서 이러한 메모리에 영구적으로 저장됩니다.
ROM은 전기를 처음 켰을 때 컴퓨터를 시작하는 데 필요한 명령을 저장합니다.이 작업을 부트 스트랩이라고합니다. ROM 칩은 컴퓨터뿐만 아니라 세탁기, 전자 레인지 등의 전자 제품에도 사용됩니다.
다음은 다양한 유형의 ROM입니다-
MROM (Masked ROM)
최초의 ROM은 사전 프로그래밍 된 데이터 또는 명령 세트를 포함하는 유선 장치였습니다. 이러한 종류의 ROM을 마스크 된 ROM이라고합니다. 저렴한 ROM입니다.
PROM (프로그래밍 가능한 읽기 전용 메모리)
PROM은 사용자가 한 번만 수정할 수있는 읽기 전용 메모리입니다. 사용자는 빈 PROM을 구입하고 PROM 프로그래머를 사용하여 원하는 내용을 입력합니다. PROM 칩 내부에는 프로그래밍 중에 타는 작은 퓨즈가 있습니다. 한 번만 프로그래밍 할 수 있으며 지울 수 없습니다.
EPROM (삭제 및 프로그래밍 가능 읽기 전용 메모리)
EPROM은 최대 40 분 동안 자외선에 노출시켜 지울 수 있습니다. 일반적으로 EPROM 지우개가이 기능을 수행합니다. 프로그래밍하는 동안 전하가 절연 된 게이트 영역에 갇혀 있습니다. 전하에 누출 경로가 없기 때문에 전하가 10 년 이상 유지됩니다. 이 전하를 소거하기 위해 자외선이 수정 창 (뚜껑)을 통과합니다. 자외선에 노출되면 전하가 소멸됩니다. 정상적인 사용 중에 석영 뚜껑은 스티커로 밀봉되어 있습니다.
EEPROM (전기적 삭제 및 프로그래밍 가능 읽기 전용 메모리)
EEPROM은 프로그래밍되고 전기적으로 지워집니다. 약 1 만 번 삭제하고 다시 프로그래밍 할 수 있습니다. 삭제와 프로그래밍 모두 약 4 ~ 10ms (밀리 초)가 걸립니다. EEPROM에서는 모든 위치를 선택적으로 지우고 프로그래밍 할 수 있습니다. EEPROM은 전체 칩을 지우지 않고 한 번에 한 바이트 씩 지울 수 있습니다. 따라서 재 프로그래밍 프로세스는 유연하지만 느립니다.
직렬 액세스 메모리
순차 액세스는 시스템이 필요한 데이터를 찾을 때까지 메모리 주소의 처음부터 저장 장치를 검색해야 함을 의미합니다. 이러한 액세스를 지원하는 메모리 장치를 Sequential Access Memory 또는 Serial Access Memory라고합니다. 자기 테이프는 직렬 액세스 메모리의 예입니다.
직접 액세스 메모리
직접 액세스 메모리 또는 랜덤 액세스 메모리는 시스템이 사용자가 원하는 정보로 직접 이동할 수있는 조건을 나타냅니다. 이러한 액세스를 지원하는 메모리 장치를 직접 액세스 메모리라고합니다. 자기 디스크, 광 디스크는 직접 액세스 메모리의 예입니다.
캐시 메모리
캐시 메모리는 CPU 속도를 높일 수있는 초고속 반도체 메모리입니다. CPU와 메인 메모리 사이의 버퍼 역할을합니다. CPU에서 가장 많이 사용하는 데이터 및 프로그램 부분을 보관하는 데 사용됩니다. 데이터 및 프로그램의 일부는 CPU가 액세스 할 수있는 운영 체제에 의해 디스크에서 캐시 메모리로 전송됩니다.
장점
- 캐시 메모리는 주 메모리보다 빠릅니다.
- 메인 메모리에 비해 액세스 시간이 적습니다.
- 단시간에 실행할 수있는 프로그램을 저장합니다.
- 임시 사용을 위해 데이터를 저장합니다.
단점
- 캐시 메모리는 용량이 제한되어 있습니다.
- 그것은 매우 비싸다.
가상 메모리는 메모리에서 완전히 사용할 수없는 프로세스의 실행을 허용하는 기술입니다. 이 체계의 주요 눈에 띄는 장점은 프로그램이 실제 메모리보다 클 수 있다는 것입니다. 가상 메모리는 실제 메모리에서 사용자 논리 메모리를 분리하는 것입니다.
이러한 분리를 통해 더 작은 실제 메모리 만 사용할 수있는 경우 프로그래머에게 매우 큰 가상 메모리를 제공 할 수 있습니다. 다음은 전체 프로그램을 주 메모리에 완전히로드 할 필요가없는 상황입니다.
사용자가 작성한 오류 처리 루틴은 데이터 또는 계산에 오류가 발생한 경우에만 사용됩니다.
프로그램의 특정 옵션 및 기능은 거의 사용되지 않을 수 있습니다.
실제로 적은 양의 테이블 만 사용하더라도 많은 테이블에 고정 된 양의 주소 공간이 할당됩니다.
부분적으로 만 메모리에있는 프로그램을 실행할 수있는 능력은 많은 이점을 상쇄합니다.
각 사용자 프로그램을 메모리에로드하거나 스왑하는 데 필요한 I / O 수가 적습니다.
프로그램은 더 이상 사용 가능한 실제 메모리의 양에 의해 제한되지 않습니다.
각 사용자 프로그램은 더 적은 실제 메모리를 사용하고 더 많은 프로그램을 동시에 실행할 수 있으며 이에 따라 CPU 사용률과 처리량이 증가합니다.
보조 메모리
보조 메모리는 주 메모리보다 크기가 훨씬 크지 만 느립니다. 일반적으로 시스템 프로그램, 명령 및 데이터 파일을 저장합니다. 보조 메모리라고도합니다. 메인 메모리 용량이 초과 된 경우 오버플로 / 가상 메모리로도 사용할 수 있습니다. 2 차 메모리는 프로세서에서 직접 액세스 할 수 없습니다. 먼저 보조 메모리의 데이터 / 정보가 주 메모리로 전송 된 다음 CPU에서 해당 정보에 액세스 할 수 있습니다. 보조 메모리의 특성은 다음과 같습니다-
Non-volatile memory − 전원이 차단 되어도 데이터가 손실되지 않습니다.
Reusable − 데이터는 사용자가 덮어 쓰거나 삭제하지 않을 때까지 영구적으로 보조 저장소에 보관됩니다.
Reliable − 2 차 저장 장치의 물리적 안정성이 높아 2 차 저장 장치의 데이터는 안전합니다.
Convenience − 권한이있는 사람은 컴퓨터 소프트웨어를 사용하여 데이터를 빠르게 찾고 액세스 할 수 있습니다.
Capacity − 보조 스토리지는 여러 디스크 세트에 많은 양의 데이터를 저장할 수 있습니다.
Cost − 데이터를 기본 메모리보다 테이프 또는 디스크에 저장하는 것이 훨씬 저렴합니다.
마이크로 프로세싱 유닛은 전통적인 컴퓨터에서 사용되는 CPU 인 중앙 처리 장치와 동의어입니다. 마이크로 프로세서 (MPU)는 다음 작업을 수행하는 장치 또는 장치 그룹의 역할을합니다.
- 주변 장치와 통신
- 타이밍 신호 제공
- 직접적인 데이터 흐름
- 메모리의 지침에 지정된대로 컴퓨터 작업을 수행합니다.
8085 마이크로 프로세서
8085 마이크로 프로세서는 64k 메모리를 처리 할 수있는 8 비트 범용 마이크로 프로세서입니다. 이 프로세서에는 40 개의 핀이 있으며 + 5V 단일 전원 공급 장치와 3MHz 단상 클럭이 필요합니다.
블록 다이어그램
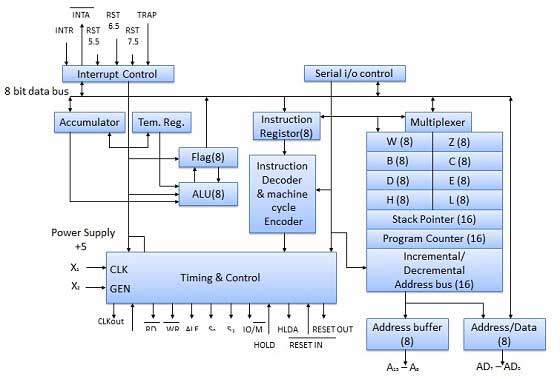
ALU
ALU는 마이크로 프로세서의 컴퓨팅 기능을 수행합니다. 누산기, 임시 레지스터, 산술 및 논리 회로 및 5 개의 플래그가 포함됩니다. 결과는 누산기 및 플래그에 저장됩니다.
블록 다이어그램

어큐뮬레이터
ALU의 일부인 8 비트 레지스터입니다. 이 레지스터는 8 비트 데이터를 저장하고 산술 및 논리 연산을 수행하는 데 사용됩니다. 연산 결과는 누산기에 저장됩니다.
도표
플래그
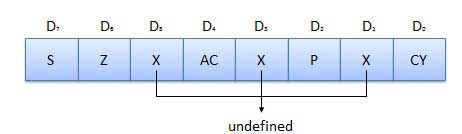
플래그는 프로그래밍 가능합니다. 명령어를 사용하여 레지스터에서 데이터를 저장하고 전송하는 데 사용할 수 있습니다. ALU에는 누산기 및 기타 레지스터의 데이터 조건에 따라 설정 및 재설정되는 5 개의 플립 플롭이 포함되어 있습니다.
S (Sign) flag− 산술 연산 실행 후 결과의 비트 D 7 이 1이면 부호 플래그가 설정됩니다. 서명 된 숫자에 사용됩니다. 주어진 바이트에서 D7 이 1이면 음수를 의미합니다. 0이면 양수임을 의미합니다.
Z (Zero) flag − ALU 연산 결과가 0이면 제로 플래그가 설정됩니다.
AC (Auxiliary Carry) flag− 산술 연산에서 D3 자리에 캐리가 생성되어 D 4 자리에 전달 되면 AC 플래그가 설정됩니다. 이 플래그는 내부적으로 BCD 작업에만 사용됩니다.
P (Parity) flag− 산술 또는 논리 연산 후 결과에 1이 짝수이면 플래그가 설정됩니다. 홀수 1이 있으면 플래그가 재설정됩니다.
C (Carry) flag − 산술 연산 결과가 캐리이면 캐리 플래그가 설정되고, 그렇지 않으면 리셋됩니다.
섹션 등록
기본적으로 저장 장치이며 명령어를 사용하여 레지스터에서 데이터를 전송합니다.
Stack Pointer (SP)− 스택 포인터는 메모리 포인터로 사용되는 16 비트 레지스터이기도합니다. 스택이라고하는 읽기 / 쓰기 메모리의 메모리 위치를 가리 킵니다. 프로그램 실행 사이에 때때로 데이터가 스택에 저장됩니다. 스택의 시작은 스택 포인터에 16 비트 주소를로드하여 정의됩니다.
Program Counter (PC)−이 16 비트 레지스터는 명령어 실행 순서를 지정하는 네 번째 연산을 다룹니다. 이 레지스터는 메모리 포인터이기도합니다. 메모리 위치에는 16 비트 주소가 있습니다. 실행 주소를 저장하는 데 사용됩니다. 프로그램 카운터의 기능은 다음 바이트를 가져올 메모리 주소를 가리키는 것입니다.
Storage registers−이 레지스터는 프로그램 실행 중에 8 비트 데이터를 저장합니다. 이러한 레지스터는 B, C, D, E, H, L로 식별됩니다. 레지스터 쌍 BC, DE 및 HL로 결합하여 16 비트 작업을 수행 할 수 있습니다.
시간 및 제어 섹션
이 장치는 클럭 펄스에 따라 마이크로 프로세서 작동을 동기화하고 마이크로 프로세서와 주변 장치 간의 원활한 통신에 필요한 제어 신호를 생성하는 역할을합니다. RD bar 및 WR bar 신호는 데이터 버스에서 데이터를 사용할 수 있는지 여부를 나타내는 동기 펄스입니다. 제어 장치는 마이크로 프로세서, 메모리 및 주변 장치 간의 데이터 흐름을 제어합니다.
PIN 다이어그램

모든 신호는 6 개의 그룹으로 분류 될 수 있습니다
| SN | 그룹 | 기술 |
|---|---|---|
| 1 | Address bus | 8085 마이크로 프로세서에는 8 개의 신호 라인, A 15 -A 8 이 있으며 단방향이며 상위 주소 버스로 사용됩니다. |
| 2 | Data bus | 신호 라인 AD7-AD0은 이중 목적을 위해 양방향입니다. 데이터 버스뿐만 아니라 하위 주소 버스로도 사용됩니다. |
| 삼 | Control signal and Status signal | 제어 신호 RD bar− 읽기 제어 신호 (액티브 로우)입니다. 활성화되면 메모리가 데이터를 읽습니다. WR bar− 쓰기 제어 신호 (액티브 로우)입니다. 선택한 메모리에 쓸 때 활성화됩니다. 상태 신호 ALU (Address Latch Enable)− ALU가 높을 때. 8085 마이크로 프로세서는 주소 버스를 사용합니다. ALU가 낮을 때. 8085 마이크로 프로세서는 데이터 버스를 사용합니다. IO/M bar− 이것은 I / O와 메모리 작동을 구별하는 데 사용되는 상태 신호입니다. 높으면 I / O 동작을 나타내고, 낮 으면 메모리 동작을 나타냅니다. S1 and S0 − 이러한 상태 신호는 I / O 및 메모리 바와 유사하여 다양한 작동을 식별 할 수 있지만 소규모 시스템에서는 거의 사용되지 않습니다. |
| 4 | Power supply and frequency signal | Vcc − + 5v 전원 공급 장치. Vss − 접지 기준. X, X−이 두 핀에 크리스탈이 연결되어 있습니다. 주파수는 내부적으로 3MHz에서 두 개의 작동 시스템으로 나뉘며 수정은 6MHz의 주파수를 가져야합니다. CLK out −이 신호는 다른 장치의 시스템 클럭으로 사용할 수 있습니다. |
| 5 | Externally initiated signal | INTR (i/p) − 인터럽트 요청. INTA bar (o/p) − 승인 인터럽트로 사용됩니다. TRAP (i/p) − 이것은 마스크 불가능한 인터럽트이며 가장 높은 우선 순위를 갖습니다. HOLD (i/p) − 실행중인 프로그램을 유지합니다. HLDA (o/p) − 확인 보류. READY (i/p) −이 신호는 느리게 응답하는 주변 장치가 데이터를 수신하거나 전송할 준비가 될 때까지 마이크로 프로세서 읽기 또는 쓰기주기를 지연시키는 데 사용됩니다. RESET IN bar −이 핀의 신호가 낮아지면 프로그램 카운터가 0으로 설정되고 버스가 3 중 상태가되고 MPU가 재설정됩니다. RESET OUT−이 신호는 MPU가 재설정 중임을 나타냅니다. 이 신호는 다른 장치를 재설정하는 데 사용할 수 있습니다. RST 7.5, RST 6.5, RST 5.5 (Request interrupt)− 프로그램 제어를 특정 메모리 위치로 전송하는 데 사용됩니다. INTR 인터럽트보다 우선 순위가 높습니다. |
| 6 | Serial I/O ports | 8085 마이크로 프로세서에는 직렬 전송 직렬 입력 데이터 및 직렬 출력 데이터를 구현하는 두 개의 신호가 있습니다. |
지시 형식
각 명령어는 컴퓨터 내의 일련의 비트로 표시됩니다. 명령어는 필드라는 비트 그룹으로 나뉩니다. 명령어가 표현되는 방식을 명령어 형식이라고합니다. 일반적으로 직사각형 상자 형태로 표시됩니다. 명령어 형식은 다음 유형일 수 있습니다.
가변 명령어 형식
이는 명령어 길이가 opcode 및 주소 지정자에 따라 달라지는 명령어 형식입니다. 예를 들어, VAX 명령어는 1 바이트에서 53 바이트 사이이며 X86 명령은 1 바이트에서 17 바이트 사이입니다.
체재

이점
이러한 형식은 코드 밀도가 좋습니다.
약점
이러한 명령어 형식은 디코딩 및 파이프 라인이 매우 어렵습니다.
고정 명령어 형식
이 유형의 명령어 형식에서는 모든 명령어의 크기가 동일합니다. 예 : MIPS, Power PC, Alpha, ARM.
체재

이점
디코딩 및 파이프 라인이 쉽습니다.
약점
코드 밀도가 좋지 않습니다.
하이브리드 명령어 형식
이 유형의 명령어 형식에서는 opcode에 의해 지정된 여러 형식 길이가 있습니다. 예 : IBM 360/70, MIPS 16, Thumb.
체재

이점
이러한 유형의 코드 밀도와 명령어 간의 이러한 절충은 디코딩하기가 매우 쉽습니다.
주소 지정 모드
주소 지정 모드는 프로세서에 주어진 데이터에 대한 주소에 액세스하는 다양한 방법을 제공합니다. 작동 데이터는 메모리 위치에 저장되며, 각 명령어는 작동해야하는 특정 데이터가 필요합니다. 데이터 주소를 지정하는 방법에는 여러 가지가 있습니다. 이러한 기술을 주소 지정 모드라고합니다.
Direct addressing mode− 직접 주소 지정 모드에서 피연산자의 주소는 명령어에 제공되며 데이터는 명령어에 제공된 메모리 위치에서 사용할 수 있습니다. 이 데이터를 원하는 위치로 이동합니다.
Indirect addressing mode− 간접 주소 지정 모드에서 명령어는 피연산자의 주소를 포함하는 레지스터를 지정합니다. 내부 RAM과 외부 RAM 모두 간접 주소 지정 모드를 통해 액세스 할 수 있습니다.
Immediate addressing mode− 즉시 주소 지정 모드에서는 누산기에서 데이터를 이동하는 피연산자에 직접 데이터가 제공됩니다. 매우 빠릅니다.
Relative addressing mode− 상대 주소 모드에서 유효 주소는 범용 프로세서 레지스터 대신 프로그램 카운터를 사용하여 인덱스 모드에 의해 결정됩니다. 이 모드를 상대 주소 모드라고합니다.
Index addressing mode− 인덱스 주소 모드에서는 레지스터 내용에 내용 값을 추가하여 피연산자의 유효 주소를 생성합니다. 이 모드를 인덱스 주소 모드라고합니다.