마이크로파 공학-마이크로파 장치

다른 시스템과 마찬가지로 마이크로 웨이브 시스템은 주로 한쪽 끝에 소스가 있고 다른 쪽 끝에로드가있는 많은 마이크로 웨이브 구성 요소로 구성되며, 모두 도파관이나 동축 케이블 또는 전송 라인 시스템과 연결됩니다.

다음은 도파관의 속성입니다.

높은 SNR
낮은 감쇠
낮은 삽입 손실

도파관 마이크로파 기능

4 개의 포트가있는 도파관을 고려하십시오. 전원이 하나의 포트에 적용되면 일부 비율로 3 개의 포트를 모두 통과하며 일부는 동일한 포트에서 반사 될 수 있습니다. 이 개념은 다음 그림에 명확하게 설명되어 있습니다.

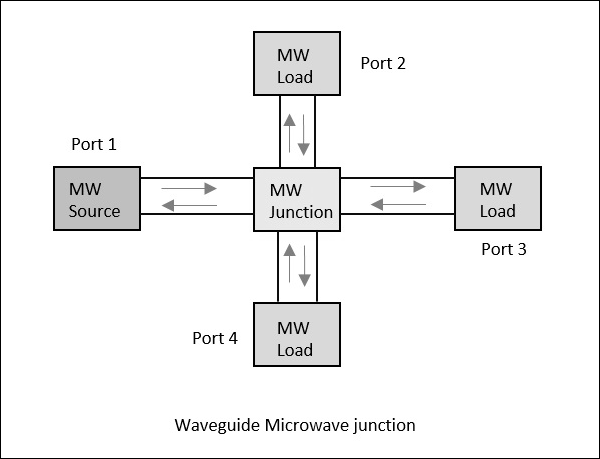
산란 매개 변수

다음 그림과 같이 2 포트 네트워크의 경우 방금 설명한 것처럼 한 포트에 전원이 공급되면 대부분의 전원이 다른 포트에서 빠져 나가고 일부는 동일한 포트로 다시 반사됩니다. 다음 그림에서V₁ 또는 V₂ 적용되면 I₁ 또는 I₂ 전류가 각각 흐릅니다.

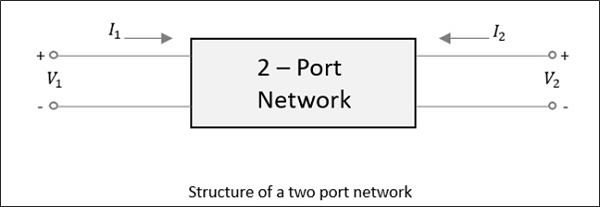
소스가 반대쪽 포트에 적용되는 경우 다른 두 가지 조합이 고려됩니다. 따라서 2 포트 네트워크의 경우 2 × 2 = 4 조합이 발생할 가능성이 높습니다.

포트를 통해 흩어질 때 연관된 힘을 가진 진행파, 마이크로파 접합은 S- 파라미터 또는 Scattering Parameters, "라고하는 행렬 형식으로 표시됩니다.Scattering Matrix".

산란 행렬

마이크로파 접합의 다양한 입력 및 출력 포트 사이의 모든 전력 관계 조합을 제공하는 정사각형 매트릭스입니다. 이 행렬의 요소는"Scattering Coefficients" 또는 "Scattering (S) Parameters".

다음 그림을 고려하십시오.

여기서 소스는 $ i ^ {th} $ 라인을 통해 연결되고 $ a_1 $은 입사 파이고 $ b_1 $는 반사파입니다.

$ b_1 $와 $ a_1 $ 사이에 관계가 주어지면

$$ b_1 = (반사 \ : \ : 계수) a_1 = S_ {1i} a_1 $$

어디

$ S_ {1i} $ = $ 1 ^ {st} $ 라인의 반사 계수 (여기서 $ i $는 입력 포트이고 $ 1 $는 출력 포트)
$ 1 $ = $ 1 ^ {st} $ 라인에서 반사
$ i $ = $ i ^ {th} $ 라인에 연결된 소스

임피던스가 일치하면 전력이 부하로 전달됩니다. 부하 임피던스가 특성 임피던스와 일치하지 않는 경우는 거의 없습니다. 그런 다음 반사가 발생합니다. 즉, 다음과 같은 경우 반사가 발생합니다.

$$ Z_l \ neq Z_o $$

그러나 이러한 불일치가 둘 이상의 포트 (예 : $ 'n'$ 포트)에있는 경우 $ i = 1 $ ~ $ n $입니다 ($ i $는 $ 1 $에서 $ n $까지의 모든 라인이 될 수 있기 때문에).

따라서 우리는

$$ b_1 = S_ {11} a_1 + S_ {12} a_2 + S_ {13} a_3 + ............... + S_ {1n} a_n $$

$$ b_2 = S_ {21} a_1 + S_ {22} a_2 + S_ {23} a_3 + ............... + S_ {2n} a_n $$

$$. $$

$$ b_n = S_ {n1} a_1 + S_ {n2} a_2 + S_ {n3} a_3 + ............... + S_ {nn} a_n $$

이 모든 것이 매트릭스 형태로 유지되면

$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \\. \\. \\. \\ b_n \ end {bmatrix} = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13 } & ... & S_ {1n} \\ S_ {21} & S_ {22} & S_ {23} & ... & S_ {2n} \\. &. &. & ... &. \\. &. &. & ... &. \\. &. &. & ... &. \\ S_ {n1} & S_ {n2} & S_ {n3} & ... & S_ {nn} \\ \ end {bmatrix} \ times \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \\. \ \. \\. \\ a_n \ end {bmatrix} $$

Column matrix $ [b] $ Scattering matrix $ [S] $Matrix $ [a] $

열 행렬 $ \ left [b \ right] $는 반사파 또는 출력에 해당하고 행렬 $ \ left [a \ right] $는 입사 파 또는 입력에 해당합니다. $ n \ x n $ 정도의 산란 열 행렬 $ \ left [s \ right] $는 반사 계수와 투과 계수를 포함합니다. 따라서,

$$ \ 왼쪽 [b \ 오른쪽] = \ 왼쪽 [S \ 오른쪽] \ 왼쪽 [a \ 오른쪽] $$