마이크로파 엔지니어링-퀵 가이드
전자기 스펙트럼은 전체 범위의 전자기 복사로 구성됩니다. 방사선은 전파되는 동안 이동하고 퍼지는 에너지입니다. 전자기 스펙트럼을 만드는 전자기 복사 유형은 다음 스크린 샷에 나와 있습니다.
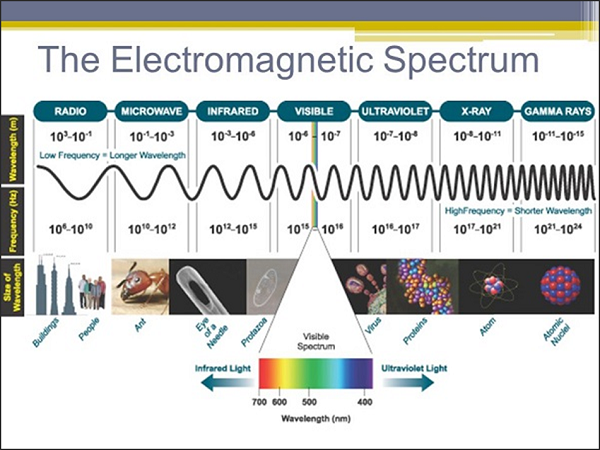
이제 마이크로파의 속성을 살펴 보겠습니다.
마이크로파의 특성
다음은 전자 레인지의 주요 속성입니다.
마이크로파는 더 짧은 파장으로 전자기 에너지를 방출하는 파동입니다.
마이크로파는 전리층에 반사되지 않습니다.
마이크로파는 직선으로 이동하며 전도 표면에 반사됩니다.
마이크로파는 짧은 거리 내에서 쉽게 감쇠됩니다.
마이크로파 전류는 케이블의 얇은 층을 통해 흐를 수 있습니다.
마이크로파의 장점
다음과 같은 마이크로파의 많은 장점이 있습니다-
더 큰 대역폭을 지원하므로 더 많은 정보가 전송됩니다. 이러한 이유로 마이크로파는 지점 간 통신에 사용됩니다.
더 많은 안테나 이득이 가능합니다.
대역폭이 많을수록 더 높은 데이터 속도가 전송됩니다.
주파수가 높을수록 안테나 크기가 줄어 듭니다.
신호의 주파수가 높기 때문에 전력 소비가 적습니다.
시선 전파를 사용하면 페이딩 효과가 감소합니다.
레이더 시스템에 효과적인 반사 영역을 제공합니다.
고용량 위성 및 지상파 통신이 가능합니다.
저가의 소형 마이크로파 부품을 개발할 수 있습니다.
사용 가능한 모든 작동 주파수 범위에서 다양한 응용 분야에서 효과적인 스펙트럼 사용.
마이크로파의 단점
다음과 같은 마이크로파의 몇 가지 단점이 있습니다-
- 장비 비용 또는 설치 비용이 높습니다.
- 그들은 무겁고 더 많은 공간을 차지합니다.
- 전자기 간섭이 발생할 수 있습니다.
- 온도에 따른 유전 특성의 변화가 발생할 수 있습니다.
- 전력의 본질적인 비 효율성.
마이크로파의 응용
다른 방사선에는 불가능한 마이크로파에 대한 다양한 응용 프로그램이 있습니다. 그들은-
무선 통신
- 장거리 전화
- Bluetooth
- WIMAX 운영
- 야외 방송 전송
- 방송 보조 서비스
- 원격 픽업 장치
- 스튜디오 / 송신기 링크
- 직접 방송 위성 (DBS)
- 개인 통신 시스템 (PCS)
- 무선 근거리 통신망 (WLAN)
- 셀룰러 비디오 (CV) 시스템
- 자동차 충돌 방지 시스템
전자
- 빠른 지터없는 스위치
- 위상 시프터
- HF 생성
- 튜닝 요소
- ECM / ECCM (Electronic Counter Measure) 시스템
- 확산 스펙트럼 시스템
상업적 용도
- 도난 경보기
- 차고 문 오프너
- 경찰 속도 감지기
- 비접촉 방식으로 식별
- 휴대폰, 호출기, 무선 LAN
- 위성 텔레비전, XM 라디오
- 동작 감지기
- 원격 감지
항해
- 글로벌 항법 위성 시스템
- GPS (Global Positioning System)
군사 및 레이더
표적의 범위와 속도를 감지하는 레이더.
SONAR 애플리케이션
항공 교통 관제
일기 예보
선박 항해
지뢰 제거 애플리케이션
속도 제한 시행
군사는 통신 및 위에서 언급 한 애플리케이션에 마이크로파 주파수를 사용합니다.
연구 응용
- 원자 공명
- 핵 공명
전파 천문학
- 우주 마이크로파 배경 방사선 표시
- 우주의 강력한 파도 감지
- 우주와 지구 대기의 많은 방사선 감지
음식 산업
- 재가열 및 요리에 사용되는 전자 레인지
- 식품 가공 응용
- 예열 애플리케이션
- Pre-cooking
- 곡물 / 콩 구이
- 감자 칩 건조
- 수분 레벨링
- 물 분자 흡수
산업 용도
- 가황 고무
- 분석 화학 응용
- 건조 및 반응 과정
- 세라믹 가공
- 폴리머 매트릭스
- 표면 수정
- 화학 증기 처리
- 분말 가공
- 의약품 살균
- 화학 합성
- 폐기물 개선
- 동력 전달
- 터널 보링
- 바위 / 콘크리트 깨기
- 석탄 이음새 끊기
- 시멘트 경화
- RF 조명
- 핵융합로
- 능동적 거부 시스템
반도체 처리 기술
- 반응성 이온 에칭
- 화학 기상 증착
분광학
- 전자 상자성 공명 (EPR 또는 ESR) 분광법
- 화학 물질에서 짝을 이루지 않은 전자에 대해 알기
- 물질의 자유 라디칼을 알기 위해
- 전자 화학
의료 응용
- 하트 비트 모니터링
- 폐수 감지
- 종양 탐지
- 지역 고열
- 치료 응용
- 지역 난방
- Angioplasty
- 마이크로파 단층 촬영
- 마이크로파 음향 이미징
전파를 전파하기 위해서는 매체가 필요합니다. 다른 유형의 전송 라인은 마이크로파의 전파에 사용됩니다. 다음 장에서 그들에 대해 알아 보겠습니다.
ㅏ transmission line한 지점에서 다른 지점으로 에너지를 전달하는 커넥터입니다. 송전선로 이론 연구는 전력 및 장비의 효과적인 사용에 도움이됩니다.
기본적으로 4 가지 유형의 전송선이 있습니다.
- 2 선식 병렬 전송선
- 동축 선
- 스트립 형 기판 전송 라인
- Waveguides
전송 중 또는 수신 중에는 전력 낭비없이 에너지 전송을 효과적으로 수행해야합니다. 이를 달성하기 위해 고려해야 할 몇 가지 중요한 매개 변수가 있습니다.
전송선의 주요 매개 변수
전송선의 중요한 매개 변수는 저항, 인덕턴스, 커패시턴스 및 컨덕턴스입니다.
저항과 인덕턴스를 함께 전송선이라고합니다. impedance.
커패시턴스와 컨덕턴스는 함께 admittance.
저항
전송 라인이 만들어지는 재료가 제공하는 저항은 특히 짧은 라인의 경우 상당한 양이 될 것입니다. 라인 전류가 증가함에 따라 옴 손실 $ \ left (I ^ {2} R \ : loss \ right) $ 또한 증가합니다.
저항 $R$ 길이의 지휘자의 "$l$" 및 단면 "$a$" 다음과 같이 표현됩니다.
$$ R = \ rho \ frac {l} {a} $$
어디
?? $ \ rho $ = 일정한 도체 재료의 저항.
전류의 온도와 주파수는 라인의 저항에 영향을 미치는 주요 요소입니다. 도체의 저항은 온도 변화에 따라 선형 적으로 변합니다. 반면 전류의 주파수가 증가하면 도체 표면에 대한 전류 밀도도 증가합니다. 그렇지 않으면 도체 중심으로 향하는 전류 밀도가 증가합니다.
즉, 전류가 도체 표면으로 더 많이 흐르고 중앙으로 덜 흐릅니다. Skin Effect.
인덕턴스
AC 전송선에서 전류는 정현파로 흐릅니다. 이 전류는 전기장에 수직 인 자기장을 유도하며 이는 정현파로도 변합니다. 이것은 패러데이의 법칙으로 잘 알려져 있습니다. 필드는 다음 그림에 설명되어 있습니다.

이 다양한 자기장은 도체에 일부 EMF를 유도합니다. 이제이 유도 전압 또는 EMF는 처음에 흐르는 전류와 반대 방향으로 흐릅니다. 반대 방향으로 흐르는이 EMF는 다음과 같은 매개 변수로 동일하게 표시됩니다.Inductance, 이것은 현재의 이동에 반대하는 속성입니다.
"로 표시됩니다.L". 측정 단위는"Henry(H)".
컨덕턴스
전송 라인과 접지 사이 및 위상 도체 사이에도 누설 전류가 있습니다. 이 소량의 누설 전류는 일반적으로 절연체 표면을 통해 흐릅니다. 이 누설 전류의 역은 다음과 같이 불립니다.Conductance. "로 표시됩니다.G".
라인 전류의 흐름은 인덕턴스와 관련되고 두 지점 간의 전압 차이는 커패시턴스와 관련됩니다. 인덕턴스는 자기장과 관련이 있고 커패시턴스는 전기장과 관련이 있습니다.
정전 용량
사이의 전압 차이 Phase conductors도체 사이에 전기장이 발생합니다. 두 도체는 평행 판과 같으며 그 사이의 공기는 유전체가됩니다. 이 패턴은 도체 사이에 커패시턴스 효과를 발생시킵니다.
특성 임피던스
균일 한 무손실 전송선을 고려하면 한 방향으로 진행하는 파동에 대해 반사가없는 해당 선을 따라 전압과 전류의 진폭 비율을 다음과 같이 부릅니다. Characteristic impedance.
$ Z_0 $로 표시됩니다.
$$ Z_0 = \ sqrt {\ frac {전압 \ : \ : 파동 \ : \ : 값} {전류 \ : \ : 파동 \ : \ : 값}} $$
$$ Z_0 = \ sqrt {\ frac {R + jwL} {G + jwC}} $$
무손실 회선의 경우 $ R_0 = \ sqrt {\ frac {L} {C}} $
$ L $ & $ C $는 단위 길이 당 인덕턴스와 커패시턴스입니다.
임피던스 매칭
부하로의 최대 전력 전송을 달성하려면 임피던스 매칭을 수행해야합니다. 이 임피던스 매칭을 달성하려면 다음 조건을 충족해야합니다.
부하의 저항은 소스의 저항과 같아야합니다.
$$ R_L = R_S $$
부하의 리액턴스는 소스의 리액턴스와 같지만 부호가 반대 여야합니다.
$$ X_L = -X_S $$
즉, 소스가 유도 성이면 부하가 용량 성이어야하며 그 반대의 경우도 마찬가지입니다.
반사 계수
송전선로에서 임피던스 불일치로 인한 반사 에너지의 양을 나타내는 매개 변수를 Reflection coefficient. $ \ rho $로 표시됩니다.(rho).
이는 "부하 단자에서 입사 전압에 대한 반사 전압의 비율"로 정의 할 수 있습니다.
$$ \ rho = \ frac {reflected \ : voltage} {incident \ : voltage} = \ frac {V_r} {V_i} \ : at \ : load \ : terminal $$
장치와 전송선 사이의 임피던스가 서로 일치하지 않으면 에너지가 반사됩니다. 반사되는 에너지가 높을수록 $ \ rho $ 반사 계수의 값이 커집니다.
전압 정재파 비율 (VSWR)
입사 파가 반사되면 정상파가 형성됩니다. 형성된 정재파에는 약간의 전압이 포함되어 있습니다. 정재파의 크기는 정재파 비율로 측정 할 수 있습니다.
정재파에서 최소 전압에 대한 최대 전압의 비율은 전압 정재파 비율 (VSWR)로 정의 할 수 있습니다. "$ S $"로 표시됩니다.
$$ S = \ frac {\ left | V_ {max} \ right |} {\ left | V_ {min} \ right |} \ quad 1 \ : \ leq S \ leq \ infty $$
VSWR은 입사 파 및 반사파의 위상 추가 및 감산으로 인해 전송 라인에 존재하는 전압 정재파 패턴을 설명합니다.
따라서 다음과 같이 쓸 수도 있습니다.
$$ S = \ frac {1 + \ rho} {1-\ rho} $$
임피던스 불일치가 클수록 정재파의 진폭이 높아집니다. 따라서 임피던스가 완벽하게 일치하면
$$ V_ {최대} : V_ {최소} = 1 : 1 $$
따라서 VSWR의 값은 단일성이며 전송이 완벽 함을 의미합니다.
전송선의 효율성
전송 라인의 효율은 입력 전력에 대한 출력 전력의 비율로 정의됩니다.
$ \ % \ : 효율 \ : \ : 전송 \ : 회선 \ : \ eta = \ frac {전력 \ : 전달 \ : \ : 수신} {전력 \ : 보낸 \ : \ : \ : 전송 \ : end} \ times 100 $
전압 규정
전압 조정은 전송 라인의 송신 및 수신 끝 사이의 전압 크기 변화로 정의됩니다.
$ \ % \ : 전압 \ : 규정 = \ frac {전송 \ : 끝 \ : 전압-\ : 수신 \ : 끝 \ : 전압} {보내기 \ : 끝 \ : 전압} \ times 100 $
임피던스 불일치로 인한 손실
일치하는 부하로 종단되지 않으면 전송 라인이 손실됩니다. 이러한 손실은 감쇠 손실, 반사 손실, 전송 손실, 반사 손실, 삽입 손실 등과 같은 많은 유형입니다.
감쇠 손실
전송 라인에서 신호 흡수로 인해 발생하는 손실을 감쇠 손실이라고하며 다음과 같이 표현됩니다.
$$ 감쇠 \ : 손실 (dB) = 10 \ : log_ {10} \ left [\ frac {E_i-E_r} {E_t} \ right] $$
어디
$ E_i $ = 입력 에너지
$ E_r $ = 부하에서 입력으로의 반사 에너지
$ E_t $ = 부하로 전달 된 에너지
반사 손실
전송선의 임피던스 불일치로 인한 신호 반사로 인해 발생하는 손실을 반사 손실이라고하며 다음과 같이 표현됩니다.
$$ Reflection \ : 손실 (dB) = 10 \ : log_ {10} \ left [\ frac {E_i} {E_i-E_r} \ right] $$
어디
$ E_i $ = 입력 에너지
$ E_r $ = 부하에서 반사 된 에너지
전송 손실
전송 라인을 통해 전송하는 동안 발생하는 손실을 전송 손실이라고하며 다음과 같이 표현됩니다.
$$ 전송 \ : 손실 (dB) = 10 \ : log_ {10} \ : \ frac {E_i} {E_t} $$
어디
$ E_i $ = 입력 에너지
$ E_t $ = 전달 된 에너지
반환 손실
전송선에 의해 반사되는 전력 측정은 반사 손실이라고하며, 다음과 같이 표현됩니다.
$$ Return \ : 손실 (dB) = 10 \ : log_ {10} \ : \ frac {E_i} {E_r} $$
어디
$ E_i $ = 입력 에너지
$ E_r $ = 반사 된 에너지
삽입 손실
전송선이없는 에너지 전달과 비교하여 전송선을 사용한 에너지 전달로 인해 발생하는 손실을 삽입 손실이라고하며 다음과 같이 표현됩니다.
$$ 삽입 \ : 손실 (dB) = 10 \ : log_ {10} \ : \ frac {E_1} {E_2} $$
어디
$ E_1 $ = 송전선없이 소스에 직접 연결되었을 때 부하가받는 에너지.
$ E_2 $ = 전송 라인이 부하와 소스 사이에 연결될 때 부하가받는 에너지.
스텁 매칭
부하 임피던스가 소스 임피던스와 일치하지 않으면 "Stub Matching"이라는 방법을 사용하여 매칭을 달성하는 경우가 있습니다.
개방 또는 단락 회로 섹션을 연결하는 과정 stubs 어떤 지점 또는 지점에서 메인 라인과 션트에서 다음과 같이 불릴 수 있습니다. Stub Matching.
더 높은 마이크로파 주파수에서는 기본적으로 두 가지 스터브 매칭 기술이 사용됩니다.
단일 스텁 매칭
단일 스터브 매칭에서 특정 고정 길이의 스터브는 부하에서 어느 정도 떨어진 곳에 배치됩니다. 고정 된 주파수에만 사용됩니다. 주파수가 변경되면 스텁의 위치를 변경해야하므로 수행되지 않습니다. 이 방법은 동축 선에는 적합하지 않습니다.
이중 스텁 매칭
이중 스터드 매칭에서는 가변 길이의 두 스터브가 특정 위치에 고정됩니다. 부하가 변경되면 일치를 달성하기 위해 스텁의 길이 만 조정됩니다. 이것은 단일 주파수 매칭 장치로 실험실 실습에서 널리 사용됩니다.
다음 그림은 스텁 일치가 어떻게 보이는지 보여줍니다.
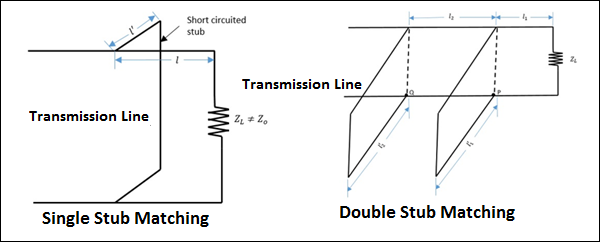
위 그림에 표시된 것처럼 단일 스터브 매칭 및 이중 스터브 매칭은 임피던스 매칭을 달성하기 위해 전송 라인에서 수행됩니다.
파동에는 전기장과 자기장이 모두 있습니다. 전기장 및 자기장의 모든 가로 성분은 z 방향에서 전기장 및 자기장의 축 성분으로부터 결정됩니다. 이것은 마이크로파에서 TE, TM, TEM 및 Hybrid와 같은 모드 형성을 허용합니다. 모드 유형을 살펴 보겠습니다.
서로 수직 인 세 방향 x, y, z에 따른 전기장 성분과 자기장 성분의 방향은 다음 그림과 같습니다.

모드 유형
마이크로파의 전파 모드는 다음과 같습니다.
TEM (Transverse Electromagnetic Wave)
이 모드에서 전기장과 자기장은 순전히 전파 방향을 가로지 릅니다. $ 'Z'$ 방향에는 구성 요소가 없습니다.
$$ E_z = 0 \ : 및 \ : H_z = 0 $$
TE (횡 전파)
이 모드에서 전기장은 순전히 전파 방향을 가로 지르는 반면 자기장은 그렇지 않습니다.
$$ E_z = 0 \ : 및 \ : H_z \ ne 0 $$
TM (횡자 기파)
이 모드에서 자기장은 순전히 전파 방향을 가로 지르는 반면 전기장은 그렇지 않습니다.
$$ E_z \ ne 0 \ : 및 \ : H_z = 0 $$
HE (하이브리드 웨이브)
이 모드에서는 전기장이나 자기장이 순전히 전파 방향을 가로 지르지 않습니다.
$$ E_z \ ne 0 \ : 및 \ : H_z \ ne 0 $$
다중 도체 라인은 일반적으로 TEM 전파 모드를 지원합니다. 전송 라인의 이론은 이동 및 복귀 경로가있는 도체 시스템, 즉 TEM 파를 지원할 수있는 도체 시스템에만 적용 할 수 있기 때문입니다.
도파관은 TE 및 TM 모드를 허용하지만 TEM 모드는 허용하지 않는 단일 도체 라인입니다. 개방형 도체 가이드는 하이브리드 웨이브를 지원합니다. 전송선의 유형은 다음 장에서 설명합니다.
기존의 개방 와이어 전송 라인은 복사 손실이 높기 때문에 마이크로파 전송에 적합하지 않습니다. 마이크로파 주파수에서 사용되는 전송선은 크게 세 가지 유형으로 분류 할 수 있습니다. 그들은-
- 다중 컨덕터 라인
- 동축 라인
- 스트립 라인
- 마이크로 스트립 라인
- 슬롯 라인
- 동일 평면상의 선 등
- 단일 도체 라인 (Waveguides)
- 직사각형 도파관
- 원형 도파관
- 타원형 도파관
- 단일 능선 도파관
- 이중 능선 도파관 등
- 열린 경계 구조
- 유전체 봉
- 개방형 도파관 등
다중 컨덕터 라인
하나 이상의 도체가있는 전송선을 다중 도체 선로라고합니다.
동축 라인
이것은 주로 고주파 애플리케이션에 사용됩니다.
동축 선은 내경이있는 내부 도체로 구성됩니다. d, 그리고 그 주위에 동심 원통형 단열재가 있습니다. 이것은 내부 직경을 가진 동심원 인 외부 도체로 둘러싸여 있습니다.D. 이 구조는 다음 그림을 보면 잘 이해됩니다.
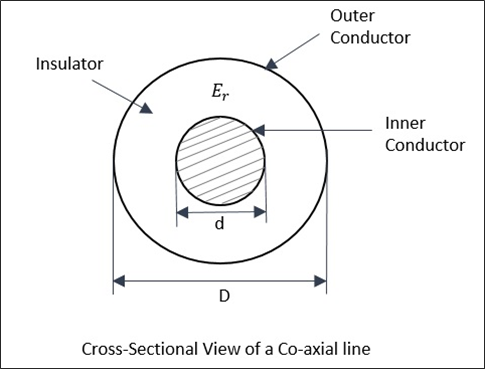
동축 케이블의 기본 및 지배적 모드는 TEM 모드입니다. 동축 케이블에는 차단 주파수가 없습니다. 모든 주파수를 통과합니다. 그러나 더 높은 주파수의 경우 일부 고차 비 TEM 모드가 전파되기 시작하여 많은 감쇠가 발생합니다.
스트립 라인
이들은 100MHz ~ 100GHz의 주파수에서 사용되는 평면 전송선입니다.
ㅏ Strip line 중앙의 얇은 전도성 스트립 폭으로 구성 ω 두께보다 큽니다 t. 두 개의 넓은 접지 판 사이에 두께 b / 2의 저손실 유전체 (ε r ) 기판 내부에 배치됩니다 . 접지 판의 너비는 판 사이의 간격보다 5 배 더 큽니다.
금속 중심 도체의 두께와 금속 접지면의 두께는 동일합니다. 다음 그림은 스트립 라인 구조의 단면도를 보여줍니다.
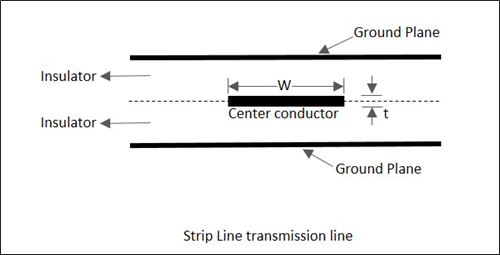
스트립 라인의 기본 및 지배적 모드는 TEM 모드입니다. 에 대한b<λ/2, 가로 방향으로 전파되지 않습니다. 스트립 라인의 임피던스는 폭 비율에 반비례합니다.ω 내부 도체의 거리 b 접지면 사이.
마이크로 스트립 라인
스트립 라인은 조정 및 튜닝을 위해 접근 할 수 없다는 단점이 있습니다. 이는 능동 또는 수동 장치를 장착 할 수있는 마이크로 스트립 라인에서 방지되며 회로가 제작 된 후 약간의 조정이 가능합니다.
마이크로 스트립 라인은 비대칭 평행 플레이트 전송 라인으로, 바닥에 금속 화 된 접지가 있고 상단에 두께가있는 얇은 전도성 스트립이있는 유전체 기판이 있습니다.t'및 너비'ω'. 이것은 마이크로 스트립 라인을 보여주는 다음 그림을 보면 이해할 수 있습니다.
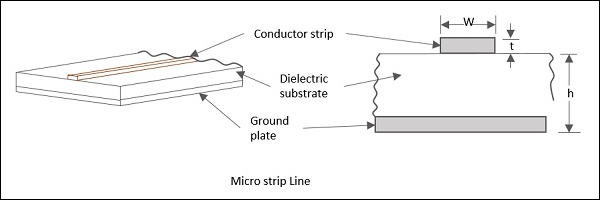
마이크로 스트립의 특성 임피던스는 스트립 선폭의 함수입니다. (ω), 두께 (t) 그리고 선과지면 사이의 거리 (h). 마이크로 스트립 라인은 임베디드 마이크로 스트립, 인버 티드 마이크로 스트립, 매달린 마이크로 스트립 및 슬롯 형 마이크로 스트립 전송 라인과 같은 다양한 유형입니다.
이 외에도 병렬 스트립 라인 및 동일 평면 스트립 라인과 같은 다른 TEM 라인도 마이크로파 집적 회로에 사용되었습니다.
기타 라인
ㅏ Parallel Strip line두 도체 전송선과 유사합니다. 준 TEM 모드를 지원할 수 있습니다. 다음 그림은이를 설명합니다.

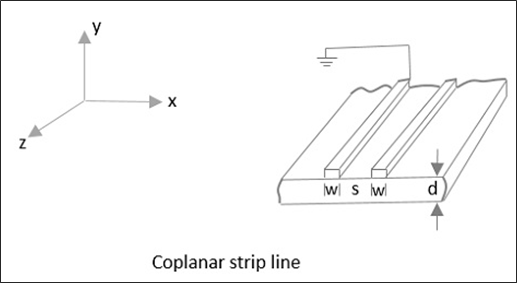
ㅏ Coplanar strip line편리한 연결을 위해 하나의 스트립이 접지 된 두 개의 전도성 스트립으로 형성되며 둘 다 동일한 기판 표면에 배치됩니다. 다음 그림은이를 설명합니다.
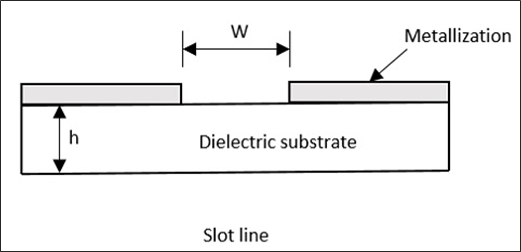
ㅏ Slot line transmission line, 유전체 기판의 전도성 코팅에있는 슬롯 또는 틈으로 구성되며이 제조 공정은 마이크로 스트립 라인과 동일합니다. 다음은 그 도식적 표현입니다.
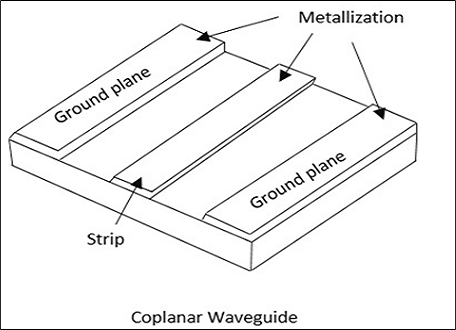
동일 평면 도파관은 유전체 슬래브의 표면에 증착되는 얇은 금속 필름 스트립으로 구성됩니다. 이 슬래브에는 동일한 표면의 스트립에 인접하고 평행하게 연결된 두 개의 전극이 있습니다. 다음 그림은이를 설명합니다.
이러한 모든 마이크로 스트립 라인은 부피가 크고 값 비싼 전송 라인을 제조하는 것이 단점이되는 마이크로파 애플리케이션에 사용됩니다.
열린 경계 구조
이들은 또한 다음과 같이 말할 수 있습니다. Open Electromagnetic Waveguides. 금속 차폐로 완전히 둘러싸여 있지 않은 도파관은 개방형 도파관으로 간주 할 수 있습니다. 여유 공간은 일종의 개방형 도파관으로 간주됩니다.
개방형 도파관은 전자기파를 안내 할 수있는 종축 대칭 및 무한 단면을 가진 물리적 장치로 정의 할 수 있습니다. 그들은 더 이상 분리되지 않는 스펙트럼을 가지고 있습니다. 마이크로 스트립 라인과 광섬유도 개방형 도파관의 예입니다.
일반적으로 신호 또는 특정 신호 대역의 주파수가 높으면 신호가 다른 신호가 누적 될 수있는 더 많은 공간을 제공하므로 대역폭 사용률이 높습니다. 그러나 고주파 신호는 감쇠되지 않고 더 먼 거리를 이동할 수 없습니다. 우리는 전송선이 신호가 더 먼 거리를 이동하도록 돕는다는 것을 연구했습니다.
마이크로파는 마이크로파 전송 라인의 일부로 작동하는 마이크로파 회로, 구성 요소 및 장치를 통해 전파되며 광범위하게 도파관이라고합니다.
튜브의 내벽에서 연속적인 반사에 의해 전자파를 전달하기위한 균일 한 단면의 중공 금속 튜브를 Waveguide.
다음 그림은 도파관의 예를 보여줍니다.
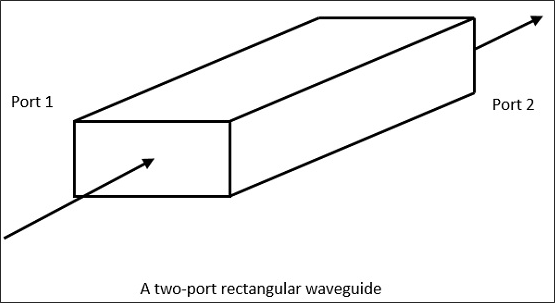
도파관은 일반적으로 마이크로파 통신에서 선호됩니다. 도파관은 중공 금속 튜브 인 특수한 형태의 전송선입니다. 전송선과 달리 도파관에는 중심 도체가 없습니다.
도파관의 주요 특징은-
튜브 벽은 분산 인덕턴스를 제공합니다.
튜브 벽 사이의 빈 공간은 분산 된 정전 용량을 제공합니다.
이들은 부피가 크고 비싸다.
도파관의 장점
다음은 도파관의 몇 가지 장점입니다.
도파관은 제조가 쉽습니다.
매우 큰 전력 (킬로와트)을 처리 할 수 있습니다.
전력 손실은 도파관에서 매우 무시할 수 있습니다.
매우 낮은 손실 (낮은 알파 감쇠 값)을 제공합니다.
마이크로파 에너지가 도파관을 통해 이동할 때 동축 케이블보다 손실이 적습니다.
도파관의 유형
도파관에는 5 가지 유형이 있습니다.
- 직사각형 도파관
- 원형 도파관
- 타원형 도파관
- 단일 능선 도파관
- 이중 능선 도파관
다음 그림은 도파관의 유형을 보여줍니다.
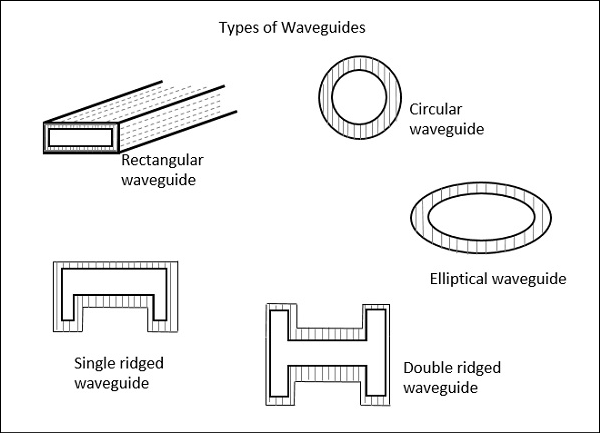
위에 표시된 도파관 유형은 중앙이 비어 있으며 구리 벽으로 구성됩니다. 이들은 내부 표면에 얇은 Au 또는 Ag 라이닝이 있습니다.
이제 전송선과 도파관을 비교해 보겠습니다.
전송 라인 대 도파관
전송선과 도파관의 주요 차이점은-
ㅏ two conductor structure TEM 파를 지원할 수있는 것은 전송선입니다.
ㅏ one conductor structure TE 파 또는 TM 파는 지원할 수 있지만 TEM 파는 지원하지 않는 것을 도파관이라고합니다.
다음 표는 전송 라인과 도파관의 차이점을 보여줍니다.
| 전송 라인 | 도파관 |
|---|---|
| TEM 웨이브 지원 | TEM 웨이브를 지원할 수 없습니다. |
| 모든 주파수는 통과 할 수 있습니다. | 차단 주파수보다 큰 주파수 만 통과 할 수 있습니다. |
| 두 도체 전송 | 하나의 도체 전송 |
| 반사가 적다 | 웨이브가 도파관의 벽에서 반사를 통해 이동합니다. |
| 그것은 특성 임피던스가 있습니다 | 그것은 파동 임피던스가 있습니다 |
| 파도의 전파는 "회로 이론"에 따릅니다. | 파동의 전파는 "장 이론"에 따릅니다. |
| 접지로의 복귀 도체가 있습니다. | 도파관 본체가 접지 역할을하므로 리턴 도체가 필요하지 않습니다. |
| 대역폭은 제한되지 않습니다 | 대역폭이 제한됨 |
| 파도가 흩어지지 않는다 | 파도가 흩어진 다 |
위상 속도
위상 속도는 파동이 위상 변화를 겪기 위해 위상을 변경하는 속도입니다. 2π라디안. 변조 될 때 사인파의 파동 성분의 속도 변화로 이해 될 수 있습니다.
위상 속도에 대한 방정식을 유도 해 보겠습니다.
정의에 따르면 위상 변화율은 2π 라디안이 고려됩니다.
즉, $λ$ / $T$ 그 후,
$$ V = \ frac {\ lambda} {T} $$
어디,
$ λ $ = 파장 및 $ T $ = 시간
$$ V = \ frac {\ lambda} {T} = \ lambda f $$
$ f = \ frac {1} {T} $ 이후
분자와 분모에 2π 그런 다음 우리는
$$ V = \ lambda f = \ frac {2 \ pi \ lambda f} {2 \ pi} $$
우리는 $ \ omega = 2 \ pi f $ and $ \ beta = \ frac {2 \ pi} {f} $
위의 방정식은 다음과 같이 쓸 수 있습니다.
$$ V = \ frac {2 \ pi f} {\ frac {2 \ pi} {\ lambda}} = \ frac {\ omega} {\ beta} $$
따라서 위상 속도에 대한 방정식은 다음과 같이 표현됩니다.
$$ V_p = \ frac {\ omega} {\ beta} $$
그룹 속도
Group Velocity는 웨이브가 도파관을 통해 전파되는 속도로 정의 할 수 있습니다. 이것은 변조 된 엔벨로프가 캐리어 단독에 비해 이동하는 속도로 이해 될 수 있습니다. 이 변조 된 파동은 도파관을 통해 이동합니다.
Group Velocity의 방정식은 다음과 같이 표현됩니다.
$$ V_g = \ frac {d \ omega} {d \ beta} $$
변조 된 엔벨로프의 속도는 일반적으로 반송파 신호보다 느립니다.
이 장에서는 마이크로파 트랜지스터 및 다양한 유형의 다이오드와 같은 마이크로파 구성 요소에 대해 설명합니다.
마이크로파 트랜지스터
마이크로파 주파수를 견딜 수있는 특수 트랜지스터를 개발할 필요가 있습니다. 따라서 마이크로파 애플리케이션의 경우silicon n-p-n transistors마이크로파 주파수에서 적절한 전력을 제공 할 수있는 것이 개발되었습니다. 일반적으로 3GHz 주파수에서 5 와트이고 이득은 5dB입니다. 이러한 트랜지스터의 단면도가 다음 그림에 나와 있습니다.
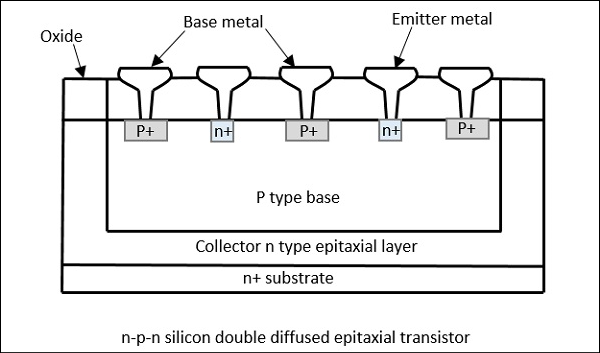
마이크로파 트랜지스터의 구성
안 n 유형 에피 택셜 층은 n+수집기를 구성하는 기판. 이에n영역에서 SiO2 층은 열적으로 성장합니다. ㅏp-base 그리고 많이 도핑 n-emitters베이스로 확산됩니다. 개구부는 옴 접촉을 위해 산화물로 만들어집니다. 연결은 병렬로 이루어집니다.
이러한 트랜지스터는 맞물림, 오버레이 또는 매트릭스로 분류되는 표면 기하학을 가지고 있습니다. 이러한 양식은 다음 그림에 나와 있습니다.
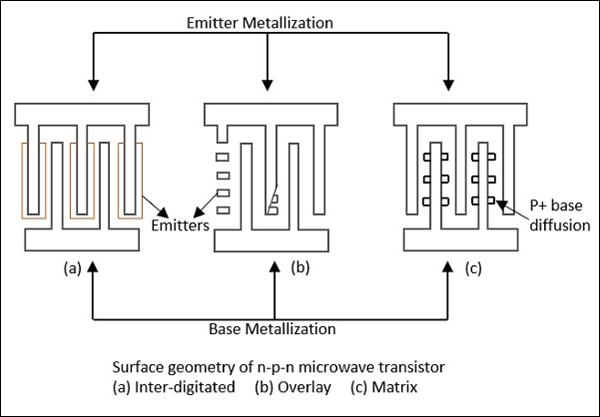
전력 트랜지스터는 세 가지 표면 구조를 모두 사용합니다.
소 신호 트랜지스터는 서로 맞물린 표면 형상을 사용합니다. 맞물림 구조는 L, S 및 C 대역의 소 신호 애플리케이션에 적합합니다.
매트릭스 지오메트리는 메시 또는 이미 터 그리드라고도합니다. 오버레이 및 매트릭스 구조는 UHF 및 VHF 영역에서 전력 장치로 유용합니다.
마이크로파 트랜지스터의 작동
마이크로파 트랜지스터에서 초기에 이미 터-베이스 및 컬렉터-베이스 접합은 역 바이어스됩니다. 마이크로파 신호를 적용하면 이미 터-베이스 접합이 순방향 바이어스됩니다. 만약p-n-p신호의 양의 피크를 적용하는 트랜지스터를 고려하면 이미 터-베이스 접합을 순방향 바이어스하여 홀이 얇은 음의베이스로 드리프트됩니다. 홀은 콜렉터와베이스 단자 사이의 바이어스 전압의 음극 단자까지 더욱 가속됩니다. 콜렉터에 연결된 부하는 전류 펄스를 수신합니다.
솔리드 스테이트 장치
고체 상태 마이크로 웨이브 장치의 분류를 수행 할 수 있습니다.
전기적 행동에 따라
-
비선형 저항 유형.
예-배리스터 (가변 저항)
-
비선형 리액턴스 유형.
예-버 랙터 (가변 반응기)
-
네거티브 저항 유형.
예-터널 다이오드, Impatt 다이오드, 건 다이오드
-
제어 가능한 임피던스 유형.
예-PIN 다이오드
-
- 건설에 따라
- 포인트 접점 다이오드
- 쇼트 키 배리어 다이오드
- 금속 산화물 반도체 장치 (MOS)
- 금속 절연 장치
여기서 언급 한 다이오드 유형은 증폭, 감지, 발전, 위상 이동, 하향 변환, 상향 변환, 변조 제한, 스위칭 등과 같은 많은 용도로 사용됩니다.
버 랙터 다이오드
역방향 바이어스 접합의 전압 가변 커패시턴스는 Varactor 다이오드라고 할 수 있습니다. 버 랙터 다이오드는 다이오드의 역방향 바이어스의 함수로 접합 커패시턴스를 변경할 수있는 반도체 장치입니다. 일반적인 Varactor 다이오드의 CV 특성과 해당 기호는 다음 그림에 나와 있습니다.
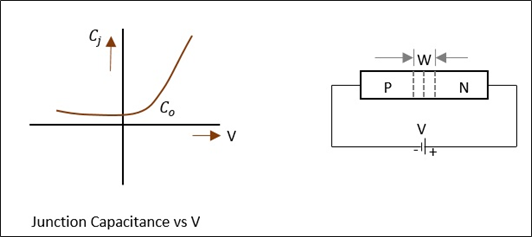
접합 커패시턴스는 적용된 전압 및 접합 설계에 따라 다릅니다. 우리는 알고 있습니다.
$$ C_j \ : \ alpha \ : V_ {r} ^ {-n} $$
어디
$ C_j $ = 접합 커패시턴스
$ V_r $ = 역 바이어스 전압
$n$ = 접합 유형을 결정하는 매개 변수
접합이 역 바이어스되면 이동 캐리어는 접합을 고갈시켜 다이오드가 커패시터로 작동하고 접합이 유전체로 작동하는 일부 커패시턴스를 발생시킵니다. 역 바이어스가 증가하면 커패시턴스가 감소합니다.
다이오드의 캡슐화에는 반도체 웨이퍼에 부착 된 전기 리드와 세라믹 케이스에 부착 된 리드가 포함되어 있습니다. 다음 그림은 마이크로파 버 랙터 다이오드의 모양을 보여줍니다.
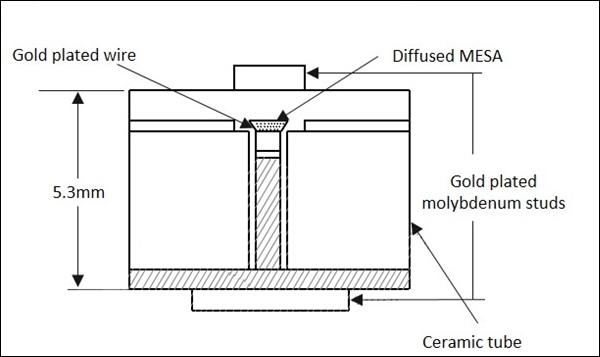
이들은 큰 전력과 큰 역 항복 전압을 처리 할 수 있습니다. 소음이 적습니다. 접합 커패시턴스의 변화가이 다이오드에서 중요한 요소이지만, 기생 저항, 커패시턴스 및 컨덕턴스는 모든 실제 다이오드와 관련이 있으므로 낮게 유지해야합니다.
버 랙터 다이오드의 응용
Varactor 다이오드는 다음 응용 분야에서 사용됩니다.
- 업 컨버전
- 파라 메트릭 증폭기
- 펄스 생성
- 펄스 형성
- 스위칭 회로
- 마이크로파 신호 변조
쇼트 키 배리어 다이오드
이것은 비선형 임피던스를 나타내는 간단한 다이오드입니다. 이 다이오드는 주로 마이크로파 감지 및 혼합에 사용됩니다.
쇼트 키 배리어 다이오드의 구성
반도체 펠릿이 금속베이스에 장착됩니다. 스프링이 장착 된 와이어가이 실리콘 펠릿에 날카로운 지점으로 연결됩니다. 이것은 동축 또는 도파관 라인에 쉽게 장착 할 수 있습니다. 다음 그림은 구조에 대한 명확한 그림을 제공합니다.
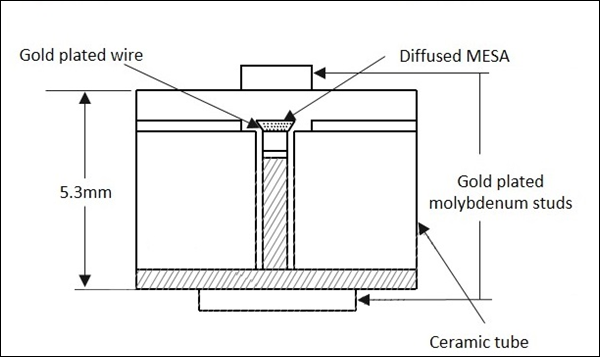
쇼트 키 배리어 다이오드의 작동
반도체와 금속 사이의 접촉으로 공핍 영역이 형성됩니다. 금속 영역은 상대적으로 공핍 폭이 더 작습니다. 접촉이 이루어지면 반도체에서 금속으로 전자 흐름이 발생합니다. 이 고갈은 반도체에 양의 공간 전하를 축적하고 전기장은 추가 흐름에 반대하여 인터페이스에 장벽을 생성합니다.
순방향 바이어스 동안 장벽 높이가 감소하고 전자가 금속에 주입되는 반면, 역방향 바이어스 동안 장벽 높이가 증가하고 전자 주입이 거의 중단됩니다.
쇼트 키 배리어 다이오드의 장점
다음과 같은 장점이 있습니다.
- 저렴한 비용
- Simplicity
- Reliable
- 소음 수치 4 ~ 5dB
쇼트 키 배리어 다이오드의 응용
이들은 다음과 같은 응용 프로그램입니다.
- 저소음 믹서
- 연속파 레이더의 밸런스드 믹서
- 마이크로파 감지기
건 효과 장치
JB Gunn은 전류의주기적인 변동을 발견했습니다. n-type GaAs인가 전압이 특정 임계 값을 초과 할 때 시편. 이 다이오드에는 두 개의 계곡이 있습니다.L & U valleys전도대에서 전자 전달은 적용된 전기장에 따라 그들 사이에서 발생합니다. 하부 L- 밸리에서 상부 U- 밸리로의 인구 반전 효과를Transfer Electron Effect 따라서 이것들은 Transfer Electron Devices (TED).
건 다이오드의 응용
Gunn 다이오드는 다음 장치에서 광범위하게 사용됩니다.
- 레이더 송신기
- 항공 교통 관제 용 트랜스 폰더
- 산업용 원격 측정 시스템
- 전력 발진기
- 논리 회로
- 광대역 선형 증폭기
물질을 통해 통과 시간과 함께 눈사태에서 전압과 전류 사이의 지연이 발생하는 과정을 네거티브 저항이라고합니다. 다이오드가 이러한 특성을 나타내도록하는 장치를 다음과 같이 부릅니다.Avalanche transit time devices.
이 범주에 속하는 장치의 예는 IMPATT, TRAPATT 및 BARITT 다이오드입니다. 각각에 대해 자세히 살펴 보겠습니다.
IMPATT 다이오드
고주파 마이크로파 애플리케이션에 사용되는 고전력 반도체 다이오드입니다. 완전한 형태의 IMPATT는IMPact ionization Avalanche Transit Time diode.
IMPATT 다이오드에 적용될 때 전압 구배는 높은 전류를 발생시킵니다. 정상적인 다이오드는 결국 이것에 의해 고장날 것입니다. 그러나 IMPATT 다이오드는이 모든 것을 견딜 수 있도록 개발되었습니다. 다이오드를 백 바이어스하기 위해 높은 전위 기울기가 적용되므로 소수 캐리어가 접합부를 가로 질러 흐릅니다.
높은 DC 전압에 중첩되는 경우 RF AC 전압을 적용하면 정공과 전자의 속도가 증가하면 충격 이온화에 의해 결정 구조에서 제거되어 추가 정공과 전자가 생성됩니다. 적용된 원래 DC 필드가이 상황을 개발하는 임계 값에 있었다면 눈사태 전류 증가로 이어지고이 프로세스가 계속됩니다. 이것은 다음 그림으로 이해할 수 있습니다.
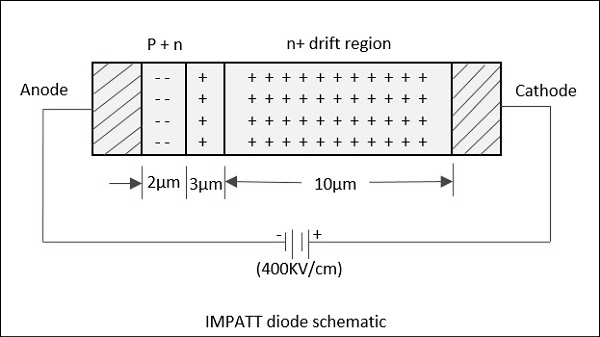
이 효과로 인해 전류 펄스는 90 °의 위상 편이를 취합니다. 그러나 거기에있는 대신 역 바이어스가 적용되어 음극쪽으로 이동합니다. 펄스가 음극에 도달하는 데 걸리는 시간은n+90 ° 위상 편이가되도록 조정됩니다. 이제 동적 RF 네거티브 저항이 존재 함이 입증되었습니다. 따라서 IMPATT 다이오드는 발진기와 증폭기의 역할을 모두 수행합니다.
다음 그림은 IMPATT 다이오드의 구조적 세부 사항을 보여줍니다.

IMPATT 다이오드의 효율은 다음과 같이 표현됩니다.
$$ \ eta = \ left [\ frac {P_ {ac}} {P_ {dc}} \ right] = \ frac {V_a} {V_d} \ left [\ frac {I_a} {I_d} \ right] $$
어디,
$ P_ {ac} $ = AC 전원
$ P_ {dc} $ = DC 전원
$ V_a \ : \ & \ : I_a $ = AC 전압 및 전류
$ V_d \ : \ & \ : I_d $ = DC 전압 및 전류
단점
다음은 IMPATT 다이오드의 단점입니다.
- 눈사태는 시끄러운 과정이므로 시끄 럽습니다.
- 튜닝 범위가 Gunn 다이오드만큼 좋지 않습니다.
응용
다음은 IMPATT 다이오드의 응용 분야입니다.
- 마이크로파 발진기
- 마이크로파 발생기
- 변조 된 출력 발진기
- 수신기 국부 발진기
- 네거티브 저항 증폭
- 침입 경보 네트워크 (높은 Q IMPATT)
- 경찰 레이더 (높은 Q IMPATT)
- 저전력 마이크로파 송신기 (높은 Q IMPATT)
- FM 텔레콤 송신기 (낮은 Q IMPATT)
- CW 도플러 레이더 송신기 (낮은 Q IMPATT)
TRAPATT 다이오드
TRAPATT 다이오드의 전체 형태는 다음과 같습니다. TRApped Plasma Avalanche Triggered Transit diode. 수백 MHz ~ GHz 사이에서 작동하는 마이크로파 발생기. 이들은 일반적으로 높은 피크 전력 다이오드입니다.n+- p-p+ 또는 p+-n-n+n 형 공핍 영역이있는 구조, 2.5에서 1.25 µm까지 다양한 너비. 다음 그림은이를 설명합니다.
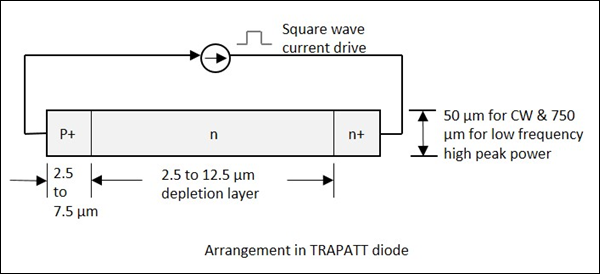
영역 뒤의 낮은 필드 영역에 갇힌 전자와 정공은 다이오드의 공핍 영역을 채우기 위해 만들어집니다. 이것은 다이오드를 통해 전파되는 높은 필드 애벌랜치 영역에 의해 수행됩니다.
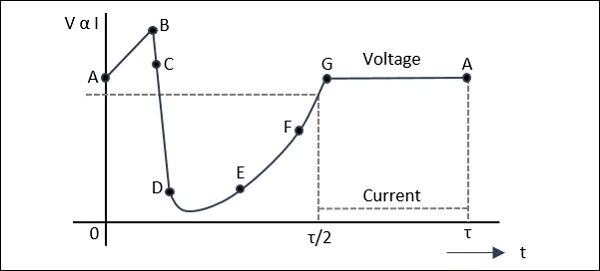
다음 그림은 AB가 충전을 나타내고 BC는 플라즈마 형성을, DE는 플라즈마 추출을, EF는 잔류 추출을, FG는 충전을 나타내는 그래프를 보여줍니다.
각 지점에서 어떤 일이 발생하는지 살펴 보겠습니다.
A:A 지점의 전압은 눈사태 고장이 발생하기에 충분하지 않습니다. A에서 열 발생으로 인한 전하 캐리어는 선형 커패시턴스처럼 다이오드를 충전합니다.
A-B:이 시점에서 전기장의 크기가 증가합니다. 충분한 수의 캐리어가 생성되면 공핍 영역 전체에서 전기장이 낮아져 전압이 B에서 C로 감소합니다.
C:이 전하는 눈사태가 계속되고 전자와 정공의 밀도가 높은 플라즈마가 생성됩니다. 전자 또는 정공이 공 핍층에서 빠져 나가지 않도록 필드가 더 눌려지고 나머지 플라즈마를 가두어 둡니다.
D: 전압은 D 지점에서 감소합니다. 전체 플라즈마 전하가 외부 전류의 단위 시간당 전하에 비해 크기 때문에 플라즈마를 제거하는 데 오랜 시간이 필요합니다.
E:E 지점에서 플라즈마가 제거됩니다. 정공과 전자의 잔류 전하는 편향 층의 한쪽 끝에 각각 남아 있습니다.
E to F: 잔류 전하가 제거되면 전압이 증가합니다.
F: 지점 F에서 내부적으로 생성 된 모든 전하가 제거됩니다.
F to G: 다이오드는 커패시터처럼 충전됩니다.
G:지점 G에서 다이오드 전류는 반 기간 동안 0이됩니다. 전압은 위 그래프와 같이 일정하게 유지됩니다. 이 상태는 전류가 다시 켜지고주기가 반복 될 때까지 계속됩니다.
눈사태 지역 속도 $ V_s $는 다음과 같이 표현됩니다.
$$ V_s = \ frac {dx} {dt} = \ frac {J} {qN_A} $$
어디
$J$ = 전류 밀도
$q$= 전자 전하 1.6 × 10 -19
$ N_A $ = 도핑 농도
눈사태 영역은 대부분의 다이오드를 빠르게 스윕하며 캐리어의 이동 시간은 다음과 같이 표시됩니다.
$$ \ tau_s = \ frac {L} {V_s} $$
어디
$ V_s $ = 포화 반송파 드리프트 속도
$ L $ = 표본의 길이
여기서 계산 된 운송 시간은 주입과 수집 사이의 시간입니다. 반복되는 동작은 출력을 증가시켜 증폭기로 만드는 반면, 회로와 션트로 연결된 마이크로파 저역 통과 필터는 발진기로 작동 할 수 있습니다.
응용
이 다이오드의 많은 응용 프로그램이 있습니다.
- 저전력 도플러 레이더
- 레이더 용 국부 발진기
- 마이크로파 비콘 랜딩 시스템
- 전파 고도계
- 위상 배열 레이더 등
BARITT 다이오드
전체 형태 BARITT Diode is BARrier Injection Transit Time diode. 이들은이 제품군의 최신 발명품입니다. 이러한 다이오드에는 IMPATT 다이오드와 같은 긴 드리프트 영역이 있지만 BARITT 다이오드의 캐리어 주입은 순방향 바이어스 접합에 의해 발생하지만 눈사태 영역의 플라즈마에서는 발생하지 않습니다.
IMPATT 다이오드에서 캐리어 주입은 충격 이온화로 인해 상당히 시끄 럽습니다. BARITT 다이오드에서는 노이즈를 방지하기 위해 공핍 영역을 펀칭하여 캐리어 주입이 제공됩니다. BARITT 다이오드의 네거티브 저항은 p- 타입 재료로 만들어진 다이오드의 컬렉터 끝으로 주입 된 홀의 드리프트 때문에 얻어집니다.
다음 그림은 BARITT 다이오드의 구조적 세부 사항을 보여줍니다.
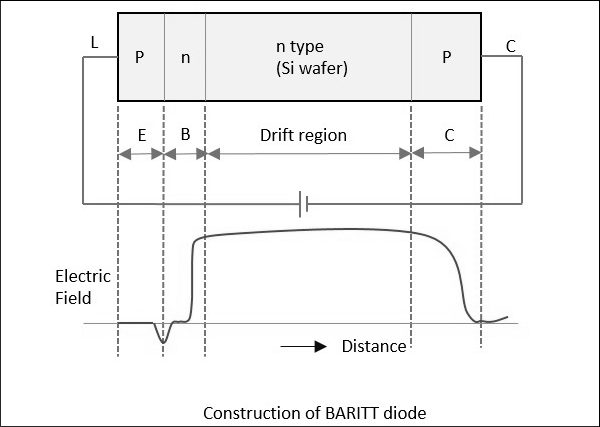
에 대한 m-n-m BARITT 다이오드, Ps-Si 쇼트 키 장벽은 금속과 접촉합니다. n-type Si wafer사이. 인가 전압 (30v 이상)에 따른 전류의 급격한 증가는 반도체에 열 이온 정공 주입으로 인한 것입니다.
임계 전압 $ (Vc) $는 도핑 상수 $ (N) $, 반도체 길이 $ (L) $ 및 다음과 같이 표현되는 반도체 유전 유전율 $ (\ epsilon S) $에 따라 달라집니다.
$$ V_c = \ frac {qNL ^ 2} {2 \ epsilon S} $$
모 놀리 식 마이크로파 집적 회로 (MMIC)
마이크로 웨이브 IC는 무게가 작고 크기가 작고 신뢰성이 높고 재현성이 뛰어 나기 때문에 기존 도파관 또는 동축 회로에 대한 최상의 대안입니다. 모 놀리 식 마이크로파 집적 회로에 사용되는 기본 재료는 다음과 같습니다.
- 기판 재료
- 도체 재료
- 유전체 필름
- 저항 막
이들은 이상적인 특성과 높은 효율성을 갖도록 선택되었습니다. 회로 요소가 제작되는 기판은 재료의 유전 상수가 높아야하고 다른 이상적인 특성과 함께 낮은 손실 계수로 높아야하기 때문에 중요합니다. 사용되는 기판 재료는 GaAs, 페라이트 / 가넷, 알루미늄, 베릴륨, 유리 및 루틸입니다.
전도체 재료는 높은 전도도, 낮은 온도 저항 계수, 기판 및 에칭 등에 대한 우수한 접착력을 갖도록 선택됩니다. 알루미늄, 구리, 금 및 은은 주로 전도체 재료로 사용됩니다. 유전체 재료와 저항 재료는 저손실과 우수한 안정성을 갖도록 선택되었습니다.
제작 기술
하이브리드 집적 회로에서 반도체 장치와 수동 회로 소자는 유전체 기판에 형성됩니다. 수동 회로는 분산 또는 집중 요소이거나 둘 다의 조합입니다.
하이브리드 집적 회로에는 두 가지 유형이 있습니다.
- 하이브리드 IC
- 미니어처 하이브리드 IC
위의 두 공정 모두에서 하이브리드 IC는 단일 레이어 금속 화 기술을 사용하여 IC에서 제조 된 분산 회로 요소를 사용하는 반면 미니어처 하이브리드 IC는 다중 레벨 요소를 사용합니다.
대부분의 아날로그 회로는 메조 절연 기술을 사용하여 FET 및 다이오드에 사용되는 활성 n 형 영역을 분리합니다. 평면 회로는 반 절연 기판에 이온을 주입하여 제조되며, 절연을 제공하기 위해 영역이 마스킹됩니다.
"Via hole"기술은 다음 그림에 표시된 GaAs FET에서 접지에 연결된 소스 전극과 소스를 연결하는 데 사용됩니다.

MMIC에는 많은 응용 프로그램이 있습니다.
- 군사 통신
- Radar
- ECM
- 위상 배열 안테나 시스템
- 확산 스펙트럼 및 TDMA 시스템
비용 효율적이며 DTH, 통신 및 계측 등과 같은 많은 국내 소비자 애플리케이션에도 사용됩니다.
다른 시스템과 마찬가지로 마이크로 웨이브 시스템은 주로 한쪽 끝에 소스가 있고 다른 쪽 끝에로드가있는 많은 마이크로 웨이브 구성 요소로 구성되며, 모두 도파관이나 동축 케이블 또는 전송 라인 시스템과 연결됩니다.
다음은 도파관의 속성입니다.
- 높은 SNR
- 낮은 감쇠
- 낮은 삽입 손실
도파관 마이크로파 기능
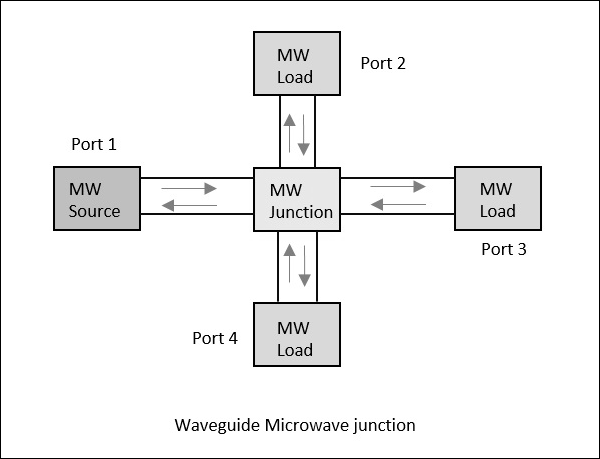
4 개의 포트가있는 도파관을 고려하십시오. 전원이 하나의 포트에 적용되면 일부 비율로 3 개의 포트를 모두 통과하며 일부는 동일한 포트에서 반사 될 수 있습니다. 이 개념은 다음 그림에 명확하게 설명되어 있습니다.
산란 매개 변수
다음 그림과 같이 2 포트 네트워크의 경우 방금 설명한 것처럼 한 포트에 전원이 공급되면 대부분의 전원이 다른 포트에서 빠져 나가고 일부는 동일한 포트로 다시 반사됩니다. 다음 그림에서V1 또는 V2 적용되면 I1 또는 I2 전류가 각각 흐릅니다.
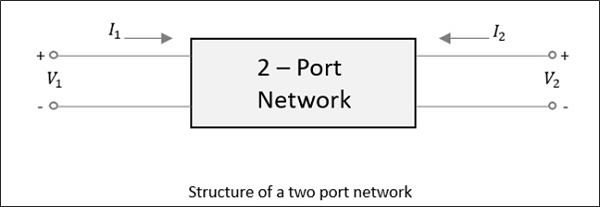
소스가 반대쪽 포트에 적용되는 경우 다른 두 가지 조합이 고려됩니다. 따라서 2 포트 네트워크의 경우 2 × 2 = 4 조합이 발생할 가능성이 높습니다.
포트를 통해 흩어질 때 연관된 힘을 가진 진행파, 마이크로파 접합은 S- 파라미터 또는 Scattering Parameters, "라고하는 행렬 형식으로 표시됩니다.Scattering Matrix".
산란 행렬
마이크로파 접합의 다양한 입력 및 출력 포트 사이의 모든 전력 관계 조합을 제공하는 정사각형 매트릭스입니다. 이 행렬의 요소는"Scattering Coefficients" 또는 "Scattering (S) Parameters".
다음 그림을 고려하십시오.

여기서 소스는 $ i ^ {th} $ 라인을 통해 연결되고 $ a_1 $은 입사 파이고 $ b_1 $는 반사파입니다.
$ b_1 $와 $ a_1 $ 사이에 관계가 주어지면
$$ b_1 = (반사 \ : \ : 계수) a_1 = S_ {1i} a_1 $$
어디
$ S_ {1i} $ = $ 1 ^ {st} $ 라인의 반사 계수 (여기서 $ i $는 입력 포트이고 $ 1 $는 출력 포트)
$ 1 $ = $ 1 ^ {st} $ 라인에서 반사
$ i $ = $ i ^ {th} $ 라인에 연결된 소스
임피던스가 일치하면 전력이 부하로 전달됩니다. 부하 임피던스가 특성 임피던스와 일치하지 않는 경우는 거의 없습니다. 그런 다음 반사가 발생합니다. 즉, 다음과 같은 경우 반사가 발생합니다.
$$ Z_l \ neq Z_o $$
그러나 이러한 불일치가 둘 이상의 포트 (예 : $ 'n'$ 포트)에있는 경우 $ i = 1 $ ~ $ n $입니다 ($ i $는 $ 1 $에서 $ n $까지의 모든 라인이 될 수 있기 때문에).
따라서 우리는
$$ b_1 = S_ {11} a_1 + S_ {12} a_2 + S_ {13} a_3 + ............... + S_ {1n} a_n $$
$$ b_2 = S_ {21} a_1 + S_ {22} a_2 + S_ {23} a_3 + ............... + S_ {2n} a_n $$
$$. $$
$$. $$
$$. $$
$$. $$
$$. $$
$$ b_n = S_ {n1} a_1 + S_ {n2} a_2 + S_ {n3} a_3 + ............... + S_ {nn} a_n $$
이 모든 것이 매트릭스 형태로 유지되면
$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \\. \\. \\. \\ b_n \ end {bmatrix} = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13 } & ... & S_ {1n} \\ S_ {21} & S_ {22} & S_ {23} & ... & S_ {2n} \\. &. &. & ... &. \\. &. &. & ... &. \\. &. &. & ... &. \\ S_ {n1} & S_ {n2} & S_ {n3} & ... & S_ {nn} \\ \ end {bmatrix} \ times \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \\. \ \. \\. \\ a_n \ end {bmatrix} $$
Column matrix $ [b] $ Scattering matrix $ [S] $Matrix $ [a] $
열 행렬 $ \ left [b \ right] $는 반사파 또는 출력에 해당하고 행렬 $ \ left [a \ right] $는 입사 파 또는 입력에 해당합니다. $ n \ x n $ 정도의 산란 열 행렬 $ \ left [s \ right] $는 반사 계수와 투과 계수를 포함합니다. 따라서,
$$ \ 왼쪽 [b \ 오른쪽] = \ 왼쪽 [S \ 오른쪽] \ 왼쪽 [a \ 오른쪽] $$
[S] 행렬의 속성
산란 행렬은 $ [S] $ 행렬로 표시됩니다. $ [S] $ 행렬에 대한 몇 가지 표준 속성이 있습니다. 그들은-
-
$ [S] $는 항상 차수의 정방 행렬 (nxn)입니다.
$ [S] _ {n \ times n} $
-
$ [S] $는 대칭 행렬입니다.
즉, $ S_ {ij} = S_ {ji} $
-
$ [S] $는 단일 행렬입니다.
즉, $ [S] [S] ^ * = I $
행이나 열의 각 항에 다른 행이나 열의 해당 항의 켤레 복소수를 곱한 곱의 합은 0입니다. 즉,
$$ \ sum_ {i = j} ^ {n} S_ {ik} S_ {ik} ^ {*} = 0 \ : for \ : k \ neq j $$
$$ (k = 1,2,3, ... \ : n) \ : 및 \ : (j = 1,2,3, ... \ : n) $$
-
$ k ^ {th} $ 포트와 접합부 사이의 전기적 거리가 $ \ beta _kI_k $이면 $ k $를 포함하는 $ S_ {ij} $의 계수에 $ e ^ {-계수를 곱합니다. j \ beta kIk} $
다음 몇 장에서는 다양한 유형의 Microwave Tee 접합을 살펴볼 것입니다.
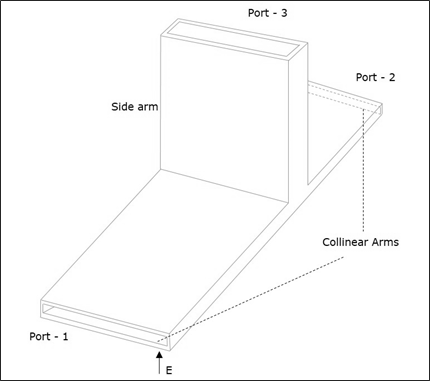
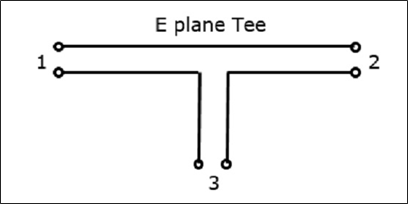
E-Plane Tee 접합은 이미 두 개의 포트가있는 직사각형 도파관의 더 넓은 치수에 간단한 도파관을 부착하여 형성됩니다. 직사각형 도파관의 암은collinear ports 즉, Port1 및 Port2, 새로운 Port3은 Side arm 또는 E-arm. 그의 E-plane Tee는Series Tee.
측면 암의 축이 전기장과 평행하기 때문에이 접합을 E-Plane Tee 접합이라고합니다. 이것은 또한Voltage 또는 Series junction. 포트 1과 2는 서로 180 ° 위상이 다릅니다. E-plane tee의 단면 세부 사항은 다음 그림에서 이해할 수 있습니다.
다음 그림은 병렬 포트를 형성하기 위해 사이드 암이 양방향 도파관에 연결하는 것을 보여줍니다.
E-Plane Tee의 특성
E-Plane Tee의 속성은 $ [S] _ {3x3} $ 행렬로 정의 할 수 있습니다.
3 개의 가능한 입력과 3 개의 가능한 출력이 있기 때문에 3x3 매트릭스입니다.
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {21} & S_ {22} & S_ {23} \\ S_ {31} & S_ {32 } & S_ {33} \ end {bmatrix} $ ........ Equation 1
산란 계수 $ S_ {13} $ 및 $ S_ {23} $는 포트 3의 입력에서 180 ° 위상이 다릅니다.
$ S_ {23} = -S_ {13} $........ Equation 2
포트는 교차점과 완벽하게 일치합니다.
$ S_ {33} = 0 $........ Equation 3
대칭 속성에서
$ S_ {ij} = S_ {ji} $
$ S_ {12} = S_ {21} \ : \ : S_ {23} = S_ {32} \ : \ : S_ {13} = S_ {31} $........ Equation 4
방정식 3과 4를 고려하면 $ [S] $ 행렬은 다음과 같이 쓸 수 있습니다.
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & -S_ {13} \\ S_ {13} & -S_ {13} & 0 \ end {bmatrix} $........ Equation 5
대칭성을 고려할 때 미지수가 4 개 있다고 말할 수 있습니다.
Unitary 속성에서
$$ [S] [S] \ ast = [I] $$
$$ \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & -S_ {13} \\ S_ {13} & -S_ {13} & 0 \ end {bmatrix} \ : \ begin {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} & S_ {13} ^ {*} \\ S_ {12} ^ {*} & S_ {22} ^ {*} & -S_ {13} ^ {*} \\ S_ {13} ^ {*} & -S_ {13} ^ {*} & 0 \ end {bmatrix} = \ begin { bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
곱하면,
(R을 행으로, C를 열로 표시)
$ R_1C_1 : S_ {11} S_ {11} ^ {*} + S_ {12} S_ {12} ^ {*} + S_ {13} S_ {13} ^ {*} = 1 $
$ \ 왼쪽 | S_ {11} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {11} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {11} \ 오른쪽 | ^ 2 = 1 $........ Equation 6
$ R_2C_2 : \ left | S_ {12} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {22} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {13} \ 오른쪽 | ^ 2 = 1 $......... Equation 7
$ R_3C_3 : \ 왼쪽 | S_ {13} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {13} \ 오른쪽 | ^ 2 = 1 $......... Equation 8
$ R_3C_1 : S_ {13} S_ {11} ^ {*}-S_ {13} S_ {12} ^ {*} = 1 $ ......... Equation 9
방정식 6과 7을 동일시하면
$ S_ {11} = S_ {22} $ ......... Equation 10
방정식 8에서
$ 2 \ 남음 | S_ {13} \ right | ^ 2 \ quad 또는 \ quad S_ {13} = \ frac {1} {\ sqrt {2}} $......... Equation 11
방정식 9에서
$ S_ {13} \ 왼쪽 (S_ {11} ^ {*}-S_ {12} ^ {*} \ 오른쪽) $
또는 $ S_ {11} = S_ {12} = S_ {22} $ ......... Equation 12
방정식 6의 방정식 10, 11, 12를 사용하여,
우리는 얻는다,
$ \ 왼쪽 | S_ {11} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {11} \ 오른쪽 | ^ 2 + \ frac {1} {2} = 1 $
$ 2 \ 남음 | S_ {11} \ right | ^ 2 = \ frac {1} {2} $
또는 $ S_ {11} = \ frac {1} {2} $ ......... Equation 13
$ [S] $ 행렬에서 위 방정식의 값을 대체합니다.
우리는
$$ \ 왼쪽 [S \ 오른쪽] = \ begin {bmatrix} \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac { 1} {2} & \ frac {1} {2} &-\ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} &-\ frac {1} { \ sqrt {2}} & 0 \ end {bmatrix} $$
$ [b] $ = $ [S] [a] $
$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \ end {bmatrix} = \ begin {bmatrix} \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {2} & \ frac {1} {2} &-\ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2 }} &-\ frac {1} {\ sqrt {2}} & 0 \ end {bmatrix} \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \ end {bmatrix} $$
이것은 E-Plane Tee의 산란 매트릭스로, 산란 특성을 설명합니다.
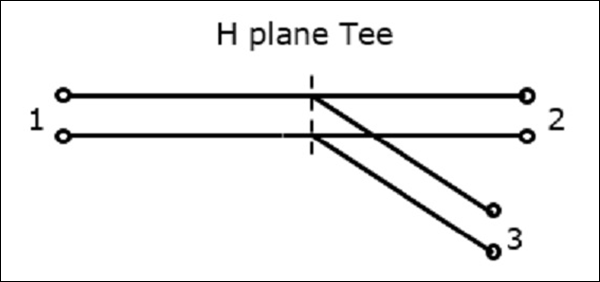
H-Plane Tee 접합은 이미 두 개의 포트가있는 직사각형 도파관에 간단한 도파관을 부착하여 형성됩니다. 직사각형 도파관의 암은collinear ports 즉, Port1 및 Port2, 새로운 Port3은 Side arm 또는 H-arm. 이 H-plane Tee는Shunt Tee.
측면 암의 축이 자기장과 평행하기 때문에이 접합을 H-Plane Tee 접합이라고합니다. 이것은 또한Current junction, 자기장이 자신을 팔로 나눕니다. H- 평면 티의 단면 세부 사항은 다음 그림에서 이해할 수 있습니다.

다음 그림은 직렬 포트를 형성하기 위해 사이드 암이 양방향 도파관에 연결하는 것을 보여줍니다.
H-Plane Tee의 특성
H-Plane Tee의 속성은 $ \ left [S \ right] _ {3 \ times 3} $ 행렬로 정의 할 수 있습니다.
3 개의 가능한 입력과 3 개의 가능한 출력이 있기 때문에 3x3 매트릭스입니다.
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {21} & S_ {22} & S_ {23} \\ S_ {31} & S_ {32 } & S_ {33} \ end {bmatrix} $ ........ Equation 1
여기서 산란계 수 $ S_ {13} $ 및 $ S_ {23} $는 교차점이 평면에서 대칭이기 때문에 동일합니다.
대칭 속성에서
$ S_ {ij} = S_ {ji} $
$ S_ {12} = S_ {21} \ : \ : S_ {23} = S_ {32} = S_ {13} \ : \ : S_ {13} = S_ {31} $
항구는 완벽하게 일치합니다
$ S_ {33} = 0 $
이제 $ [S] $ 행렬은 다음과 같이 쓸 수 있습니다.
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & S_ {13} \\ S_ {13} & S_ {13 } & 0 \ end {bmatrix} $ ........ Equation 2
대칭성을 고려할 때 미지수가 4 개 있다고 말할 수 있습니다.
Unitary 속성에서
$$ [S] [S] \ ast = [I] $$
$$ \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & S_ {13} \\ S_ {13} & S_ {13} & 0 \ end {bmatrix} \ : \ begin {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} & S_ {13} ^ {*} \\ S_ {12} ^ {*} & S_ {22} ^ {*} & S_ {13} ^ {*} \\ S_ {13} ^ {*} & S_ {13} ^ {*} & 0 \ end {bmatrix} = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
곱하면,
(R을 행으로, C를 열로 표시)
$ R_1C_1 : S_ {11} S_ {11} ^ {*} + S_ {12} S_ {12} ^ {*} + S_ {13} S_ {13} ^ {*} = 1 $
$ \ 왼쪽 | S_ {11} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {12} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {13} \ 오른쪽 | ^ 2 = 1 $........ Equation 3
$ R_2C_2 : \ left | S_ {12} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {22} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {13} \ 오른쪽 | ^ 2 = 1 $......... Equation 4
$ R_3C_3 : \ 왼쪽 | S_ {13} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {13} \ 오른쪽 | ^ 2 = 1 $......... Equation 5
$ R_3C_1 : S_ {13} S_ {11} ^ {*}-S_ {13} S_ {12} ^ {*} = 0 $ ......... Equation 6
$ 2 \ 남음 | S_ {13} \ right | ^ 2 = 1 \ quad 또는 \ quad S_ {13} = \ frac {1} {\ sqrt {2}} $......... Equation 7
$ \ 왼쪽 | S_ {11} \ 오른쪽 | ^ 2 = \ 왼쪽 | S_ {22} \ 오른쪽 | ^ 2 $
$ S_ {11} = S_ {22} $ ......... Equation 8
방정식 6에서 $ S_ {13} \ left (S_ {11} ^ {*} + S_ {12} ^ {*} \ right) = 0 $
이후 $ S_ {13} \ neq 0, S_ {11} ^ {*} + S_ {12} ^ {*} = 0, \ : 또는 \ : S_ {11} ^ {*} = -S_ {12} ^ {*} $
또는 $ S_ {11} = -S_ {12} \ : \ : 또는 \ : \ : S_ {12} = -S_ {11} $......... Equation 9
이를 방정식 3에서 사용하면
이후 $ S_ {13} \ neq 0, S_ {11} ^ {*} + S_ {12} ^ {*} = 0, \ : 또는 \ : S_ {11} ^ {*} = -S_ {12} ^ {*} $
$ \ 왼쪽 | S_ {11} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {11} \ right | ^ 2 + \ frac {1} {2} = 1 \ quad 또는 \ quad 2 \ left | S_ {11} \ right | ^ 2 = \ frac {1} {2} \ quad 또는 \ quad S_ {11} = \ frac {1} {2} $..... Equation 10
방정식 8과 9에서
$ S_ {12} =-\ frac {1} {2} $......... Equation 11
$ S_ {22} = \ frac {1} {2} $......... Equation 12
방정식 2에서 방정식 7과 10, 11과 12에서 $ S_ {13} $, $ S_ {11} $, $ S_ {12} $ 및 $ S_ {22} $를 대체합니다.
우리는
$$ \ 왼쪽 [S \ 오른쪽] = \ begin {bmatrix} \ frac {1} {2} &-\ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\-\ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & \ frac {1} { \ sqrt {2}} & 0 \ end {bmatrix} $$
$ [b] $ = $ [s] [a] $
$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \ end {bmatrix} = \ begin {bmatrix} \ frac {1} {2} &-\ frac {1} {2} & \ frac {1} { \ sqrt {2}} \\-\ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt { 2}} & \ frac {1} {\ sqrt {2}} & 0 \ end {bmatrix} \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \ end {bmatrix} $$
이것은 산란 특성을 설명하는 H-Plane Tee의 산란 행렬입니다.
EH Plane Tee 접합은 두 개의 간단한 도파관을 하나는 평행하고 다른 하나는 직렬로 연결하여 이미 두 개의 포트가있는 직사각형 도파관에 연결합니다. 이것은 또한Magic Tee, 또는 Hybrid 또는 3dB coupler.
직사각형 도파관의 암은 collinear ports 즉, 포트 1과 포트 2, 포트 3은 H-Arm 또는 Sum port 또는 Parallel port. 포트 4는E-Arm 또는 Difference port 또는 Series port.
Magic Tee의 단면 세부 사항은 다음 그림으로 이해할 수 있습니다.
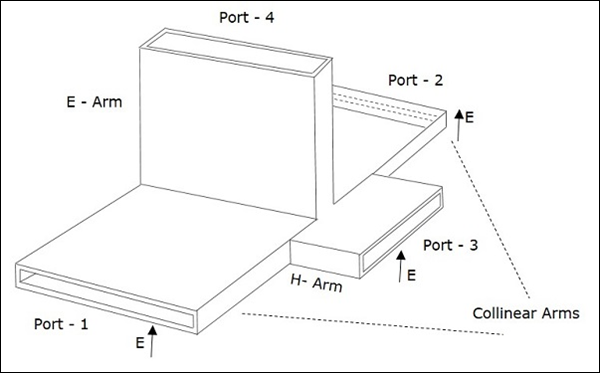
다음 그림은 병렬 및 직렬 포트를 모두 형성하기 위해 양방향 도파관에 대한 측면 암의 연결을 보여줍니다.
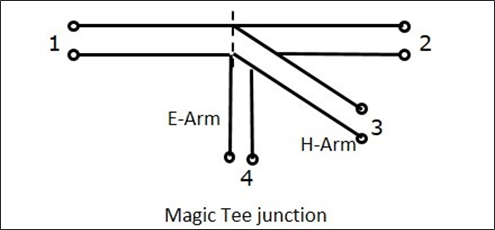
EH Plane Tee의 특징
동일한 위상과 크기의 신호가 포트 1과 포트 2로 전송되면 포트 4의 출력은 0이고 포트 3의 출력은 포트 1과 2의 추가 값이됩니다.
신호가 포트 4 (E-arm)로 전송되면 전원이 포트 1과 2 사이에서 동일하지만 반대 위상으로 분배되고 포트 3에는 출력이 없습니다. 따라서 $ S_ {34} $ = 0 .
신호가 포트 3에서 공급되면 전원이 포트 1과 2로 균등하게 분배되는 반면 포트 4에서는 출력이 없습니다. 따라서 $ S_ {43} $ = 0입니다.
신호가 동일 선상 포트 중 하나에서 공급되면 E-arm이 위상 지연을 생성하고 H-arm이 위상 전진을 생성하기 때문에 다른 동일 선상 포트에 출력이 나타나지 않습니다. 따라서 $ S_ {12} $ = $ S_ {21} $ = 0입니다.
EH 평면 티의 특성
EH Plane Tee의 속성은 $ \ left [S \ right] _ {4 \ times 4} $ 행렬로 정의 할 수 있습니다.
4 개의 가능한 입력과 4 개의 가능한 출력이 있기 때문에 4x4 매트릭스입니다.
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} & S_ {14} \\ S_ {21} & S_ {22} & S_ {23} & S_ {24} \\ S_ {31} & S_ {32} & S_ {33} & S_ {34} \\ S_ {41} & S_ {42} & S_ {43} & S_ {44} \ end {bmatrix} $ ........ Equation 1
H-Plane Tee 섹션이 있으므로
$ S_ {23} = S_ {13} $........ Equation 2
E-Plane Tee 섹션이 있으므로
$ S_ {24} = -S_ {14} $........ Equation 3
E-Arm 포트와 H-Arm 포트는 너무 격리되어있어 입력이 둘 중 하나에 적용될 경우 다른 하나가 출력을 제공하지 않습니다. 따라서 이것은 다음과 같이 지적 할 수 있습니다.
$ S_ {34} = S_ {43} = 0 $........ Equation 4
대칭 속성에서 우리는
$ S_ {ij} = S_ {ji} $
$ S_ {12} = S_ {21}, S_ {13} = S_ {31}, S_ {14} = S_ {41} $
$ S_ {23} = S_ {32}, S_ {24} = S_ {42}, S_ {34} = S_ {43} $........ Equation 5
포트 3과 4가 정션과 완벽하게 일치하면
$ S_ {33} = S_ {44} = 0 $........ Equation 6
$ [S] $ 행렬을 구하려면 위의 모든 방정식을 방정식 1에 대입하고
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} & S_ {14} \\ S_ {12} & S_ {22} & S_ {13} & -S_ {14 } \\ S_ {13} & S_ {13} & 0 & 0 \\ S_ {14} & -S_ {14} & 0 & 0 \ end {bmatrix} $........ Equation 7
단일 속성에서 $ [S] [S] ^ \ ast = [I] $
$ \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} & S_ {14} \\ S_ {12} & S_ {22} & S_ {13} & -S_ {14} \\ S_ {13} & S_ {13} & 0 & 0 \\ S_ {14} & -S_ {14} & 0 & 0 \ end {bmatrix} \ begin {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} & S_ {13} ^ {*} & S_ {14} ^ {*} \\ S_ {12} ^ {*} & S_ {22} ^ {*} & S_ {13} ^ {*} & -S_ {14} ^ {*} \\ S_ {13} & S_ {13} & 0 & 0 \\ S_ {14} & -S_ {14} & 0 & 0 \ end {bmatrix} $
$ = \ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $
$ R_1C_1 : \ 왼쪽 | S_ {11} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {12} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {13} \ 오른쪽 | ^ 2 = 1 + \ 왼쪽 | S_ {14} \ 오른쪽 | ^ 2 = 1 $......... Equation 8
$ R_2C_2 : \ left | S_ {12} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {22} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {13} \ 오른쪽 | ^ 2 = 1 + \ 왼쪽 | S_ {14} \ 오른쪽 | ^ 2 = 1 $......... Equation 9
$ R_3C_3 : \ 왼쪽 | S_ {13} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {13} \ 오른쪽 | ^ 2 = 1 $......... Equation 10
$ R_4C_4 : \ left | S_ {14} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {14} \ 오른쪽 | ^ 2 = 1 $......... Equation 11
방정식 10과 11에서 우리는
$ S_ {13} = \ frac {1} {\ sqrt {2}} $........ Equation 12
$ S_ {14} = \ frac {1} {\ sqrt {2}} $........ Equation 13
방정식 8과 9를 비교하면
$ S_ {11} = S_ {22} $ ......... Equation 14
방정식 12와 13의 값을 사용하여
$ \ 왼쪽 | S_ {11} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {12} \ 오른쪽 | ^ 2 + \ frac {1} {2} + \ frac {1} {2} = 1 $
$ \ 왼쪽 | S_ {11} \ 오른쪽 | ^ 2 + \ 왼쪽 | S_ {12} \ 오른쪽 | ^ 2 = 0 $
$ S_ {11} = S_ {22} = 0 $ ......... Equation 15
방정식 9에서 $ S_ {22} = 0 $가됩니다. ......... Equation 16
이제 포트 1과 2가 교차점에 완벽하게 일치한다는 것을 이해합니다. 이것은 4 포트 접합이므로 두 포트가 완벽하게 일치 할 때마다 다른 두 포트도 접합과 완벽하게 일치합니다.
4 개의 포트가 모두 완벽하게 일치하는 교차점을 Magic Tee Junction이라고합니다.
방정식 7의 $ [S] $ 행렬에서 12에서 16까지의 방정식을 대입하여 Magic Tee의 산란 행렬을 다음과 같이 얻습니다.
$$ [S] = \ begin {bmatrix} 0 & 0 & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ 0 & 0 & \ frac {1} {2} &-\ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & \ frac {1} {\ sqrt {2}} & 0 & 0 \\ \ frac {1} {\ sqrt {2}} &-\ frac {1} {\ sqrt {2}} & 0 & 0 \ end {bmatrix} $$
우리는 이미 알고 있습니다. $ [b] $ = $ [S] [a] $
위의 내용을 다시 작성하면
$$ \ begin {vmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \ end {vmatrix} = \ begin {bmatrix} 0 & 0 & \ frac {1} {2} & \ frac {1} {\ sqrt {2} } \\ 0 & 0 & \ frac {1} {2} &-\ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & \ frac {1} {\ sqrt {2}} & 0 & 0 \\ \ frac {1} {\ sqrt {2}} &-\ frac {1} {\ sqrt {2}} & 0 & 0 \ end {bmatrix} \ begin {vmatrix} a_1 \ \ a_2 \\ a_3 \\ a_4 \ end {vmatrix} $$
EH 평면 티의 응용
EH Plane Tee의 가장 일반적인 응용 프로그램은 다음과 같습니다.
EH Plane junction은 임피던스를 측정하는 데 사용됩니다.-null 검출기는 E-Arm 포트에 연결되고 Microwave 소스는 H-Arm 포트에 연결됩니다. 이 포트와 함께 동일 선상 포트는 브리지를 만들고 임피던스 측정은 브리지 균형을 유지하여 수행됩니다.
EH Plane Tee는 듀플렉서로 사용됩니다. 듀플렉서는 두 가지 목적을 위해 단일 안테나를 사용하여 송신기와 수신기 모두로 작동하는 회로입니다. 포트 1과 2는 분리되어 간섭하지 않는 수신기와 송신기로 사용됩니다. 안테나는 E-Arm 포트에 연결됩니다. 일치하는 부하가 반사를 제공하지 않는 H-Arm 포트에 연결됩니다. 이제 아무런 문제없이 송수신이 있습니다.
EH Plane Tee는 믹서로 사용됩니다. E-Arm 포트는 안테나와 연결되고 H-Arm 포트는 로컬 발진기와 연결됩니다. 포트 2에는 반사가없는 정합 된 부하가 있고 포트 1에는 IF 주파수를 생성하기 위해 신호 전력의 절반과 발진기 전력의 절반을 가져 오는 믹서 회로가 있습니다.
위의 응용 프로그램 외에도 EH Plane Tee 접합은 Microwave Bridge, Microwave Discriteria 등으로도 사용됩니다.
이 마이크로 웨이브 장치는 위상차가없는 두 신호를 결합하고 경로 차이가있는 신호를 피하기 위해 사용됩니다.
정상적인 3 포트 Tee 접합을 취하고 여기에 네 번째 포트를 추가하여 ratrace 접합으로 만듭니다. 이 모든 포트는 직렬 또는 병렬 접합을 사용하여 동일한 간격으로 각 링 형태로 연결됩니다.
전체 레이스의 평균 원주는 1.5λ이고 4 개의 포트 각각은 λ / 4의 거리로 분리됩니다. 다음 그림은 Rat-race 접합의 이미지를 보여줍니다.
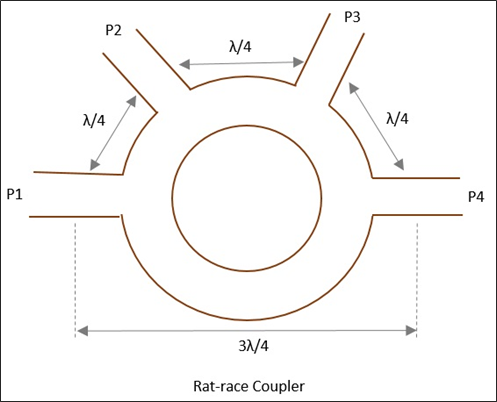
Rat-race 접합의 작동을 이해하기 위해 몇 가지 사례를 고려해 보겠습니다.
사례 1
입력 전원이 포트 1에 공급되면 똑같이 두 개의 포트로 나뉘지만 포트 2는 시계 방향으로, 포트 4는 시계 반대 방향으로 나뉩니다. 포트 3은 출력이 전혀 없습니다.
그 이유는 포트 2와 4에서 전력이 위상으로 결합되는 반면 포트 3에서는 λ / 2 경로 차이로 인해 취소가 발생하기 때문입니다.
사례 2
입력 전원이 포트 3에 공급되면 전원이 포트 2와 포트 4에 균등하게 분배되지만 포트 1에는 출력이 없습니다.
사례 3
두 개의 동일하지 않은 신호가 포트 1 자체에 적용되는 경우 출력은 포트 2와 4로 나누어 진 두 입력 신호의 합에 비례합니다. 이제 포트 3에 차동 출력이 나타납니다.
Rat-race 접합에 대한 산란 매트릭스는 다음과 같이 표현됩니다.
$$ [S] = \ begin {bmatrix} 0 & S_ {12} & 0 & S_ {14} \\ S_ {21} & 0 & S_ {23} & 0 \\ 0 & S_ {32} & 0 & S_ {34} \ \ S_ {41} & 0 & S_ {43} & 0 \ end {bmatrix} $$
응용
Rat-race junction은 두 신호를 결합하고 신호를 두 개로 나누는 데 사용됩니다.
ㅏ Directional coupler측정 목적으로 소량의 마이크로파 전력을 샘플링하는 장치입니다. 전력 측정에는 입사 전력, 반사 전력, VSWR 값 등이 포함됩니다.
방향성 결합기는 1 차 주 도파관과 2 차 보조 도파관으로 구성된 4 포트 도파관 접합입니다. 다음 그림은 방향성 커플러의 이미지를 보여줍니다.
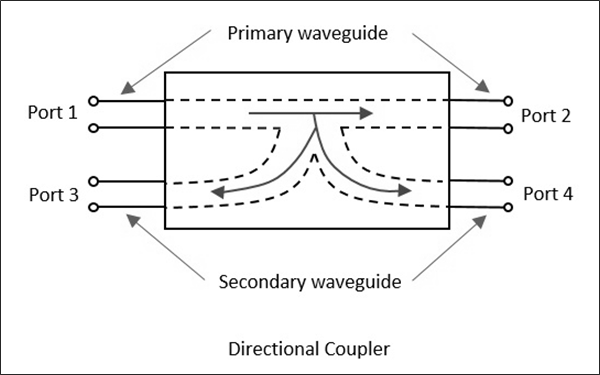
방향성 결합기는 단방향 또는 양방향 일 수있는 마이크로파 전력을 결합하는 데 사용됩니다.
방향성 커플러의 특성
이상적인 방향성 커플러의 특성은 다음과 같습니다.
모든 종단은 포트와 일치합니다.
전원이 포트 1에서 포트 2로 이동할 때 일부는 포트 4에 연결되지만 포트 3에는 연결되지 않습니다.
양방향 커플러이기도하므로 전원이 포트 2에서 포트 1로 이동할 때 일부는 포트 3에 연결되지만 포트 4에는 연결되지 않습니다.
전원이 포트 3을 통해 들어 오면 일부가 포트 2에 연결되지만 포트 1에는 연결되지 않습니다.
전원이 포트 4를 통해 들어 오면 일부가 포트 1에 연결되지만 포트 2에는 연결되지 않습니다.
포트 1과 3은 포트 2와 포트 4처럼 분리됩니다.
이상적으로는 포트 3의 출력이 0이어야합니다. 그러나 실제로는back power 다음 그림은 방향성 커플러의 전원 흐름을 나타냅니다.
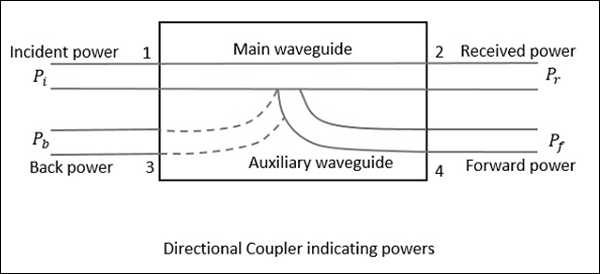
어디
$ P_i $ = 포트 1의 인시던트 전력
$ P_r $ = 포트 2에서 수신 된 전력
$ P_f $ = 포트 4의 순방향 결합 전원
$ P_b $ = 포트 3의 백 파워
다음은 방향성 커플러의 성능을 정의하는 데 사용되는 매개 변수입니다.
결합 계수 (C)
방향성 커플러의 결합 계수는 dB 단위로 측정 된 순방향 전력에 대한 입사 전력의 비율입니다.
$$ C = 10 \ : log_ {10} \ frac {P_i} {P_f} dB $$
지향성 (D)
방향성 커플러의 지향성은 dB 단위로 측정 된 후방 전력에 대한 순방향 전력의 비율입니다.
$$ D = 10 \ : log_ {10} \ frac {P_f} {P_b} dB $$
격리
방향성 커플러의 지시 속성을 정의합니다. dB 단위로 측정 한 후면 전력에 대한 입사 전력의 비율입니다.
$$ I = 10 \ : log_ {10} \ frac {P_i} {P_b} dB $$
Isolation in dB = Coupling factor + Directivity
2- 홀 방향성 커플러
이것은 동일한 주 도파관과 보조 도파관이 있지만 두 개의 작은 구멍이 공통적으로있는 방향성 커플러입니다. 이 구멍은 $ {\ lambda_g} / {4} $ 거리이며, 여기서 λg는 가이드 파장입니다. 다음 그림은 2 홀 방향성 커플러의 이미지를 보여줍니다.
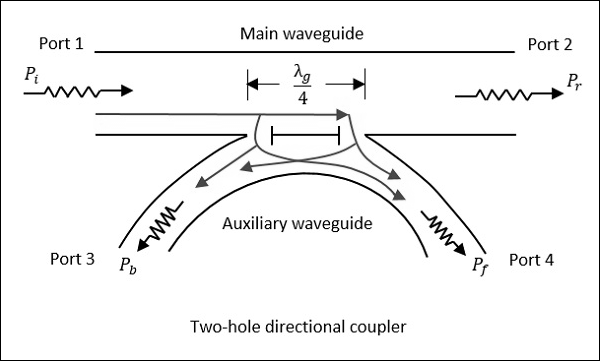
2 홀 방향성 커플러는 방향성 커플러의 이상적인 요구 사항을 충족하도록 설계되어 백 파워를 방지합니다. 포트 1과 포트 2 사이를 이동하는 동안 일부 전력은 구멍 1과 2를 통해 빠져 나갑니다.
힘의 크기는 구멍의 크기에 따라 다릅니다. 두 홀의 누설 전력은 홀 2에서 위상이 같아서 순방향 전력에 기여하는 전력을 더합니다.Pf. 그러나 홀 1에서 위상이 다르므로 서로 상쇄되고 백 파워가 발생하지 않습니다.
따라서 방향성 커플러의 지향성이 향상됩니다.
도파관 조인트
도파관 시스템은 항상 단일 부품으로 구축 될 수 없기 때문에 때로는 다른 도파관을 결합해야합니다. 이 결합은-반사 효과, 정재파 생성 및 감쇠 증가 등과 같은 문제를 방지하기 위해 신중하게 수행되어야합니다.
도파관 조인트는 불규칙성을 피하는 것 외에도 E 및 H 필드 패턴에 영향을주지 않도록주의해야합니다. 볼트 플랜지, 플랜지 조인트, 초크 조인트 등과 같은 많은 유형의 도파관 조인트가 있습니다.
마이크로파의 생성 및 증폭을 위해서는 다음과 같은 특수 튜브가 필요합니다. Microwave tubes. 그중에서도,Klystron 중요한 것입니다.
Klystron의 필수 요소는 전자빔과 공동 공진기입니다. 전자빔은 소스에서 생성되고 캐비티 클라이스트론은 신호를 증폭하는 데 사용됩니다. 전자를 수집하기 위해 끝에 수집기가 있습니다. 전체 설정은 다음 그림과 같습니다.
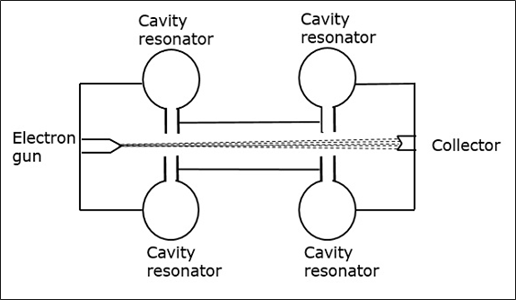
음극에서 방출되는 전자는 첫 번째 공진기를 향해 가속됩니다. 끝에있는 수집기는 공진기와 동일한 전위에 있습니다. 따라서 일반적으로 전자는 공동 공진기 사이의 간격에서 일정한 속도를 갖습니다.
처음에 첫 번째 캐비티 공진기에는 증폭되어야하는 약한 고주파 신호가 공급됩니다. 신호는 캐비티 내부의 전자기장을 시작합니다. 이 신호는 다음 그림과 같이 동축 케이블을 통해 전달됩니다.

이 장으로 인해 공동 공진기를 통과하는 전자가 변조됩니다. 두 번째 공진기에 도달하면 전자는 동일한 주파수에서 다른 EMF로 유도됩니다. 이 필드는 두 번째 캐비티에서 큰 신호를 추출 할만큼 충분히 강합니다.
공동 공진기
먼저 캐비티 공진기의 구조적 세부 사항과 작동을 이해하려고합니다. 다음 그림은 공동 공진기를 나타냅니다.
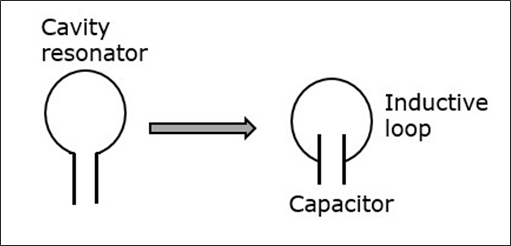
커패시터와 유도 루프로 구성된 단순한 공진 회로를이 캐비티 공진기와 비교할 수 있습니다. 도체에는 자유 전자가 있습니다. 이 극성의 전압으로 충전하기 위해 커패시터에 전하가 가해지면 많은 전자가 상부 플레이트에서 제거되어 하부 플레이트로 유입됩니다.
전자 증착이 많은 판이 음극이되고 전자 수가 적은 판이 양극이됩니다. 다음 그림은 커패시터의 전하 증착을 보여줍니다.
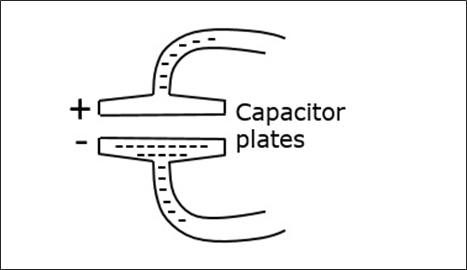
전기장 라인은 양전하에서 음으로 향합니다. 커패시터가 역 극성으로 충전되면 필드의 방향도 반전됩니다. 튜브에서 전자의 변위는 교류를 구성합니다. 이 교류는 커패시터의 전기장과 위상이 다른 교류 자기장을 발생시킵니다.
자기장이 최대 강도 일 때 전기장은 0이고 잠시 후 자기장이 0에있는 동안 전기장은 최대가됩니다. 이 힘의 교환은주기 동안 발생합니다.
폐쇄 형 공진기
커패시터의 값과 루프의 유도 성이 작을수록 발진 또는 공진 주파수가 높아집니다. 루프의 인덕턴스가 매우 작기 때문에 고주파수를 얻을 수 있습니다.
더 높은 주파수 신호를 생성하기 위해 다음 그림과 같이 더 많은 유도 루프를 병렬로 배치하여 인덕턴스를 더 줄일 수 있습니다. 그 결과 매우 높은 주파수를 갖는 폐쇄 공진기가 형성됩니다.
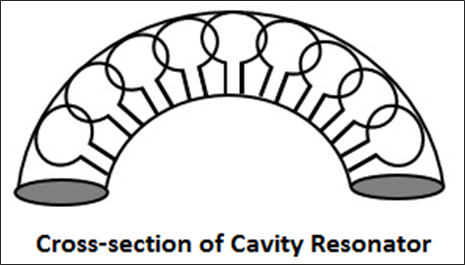
폐쇄 형 공진기에서 전기장과 자기장은 공동 내부로 제한됩니다. 공동의 첫 번째 공진기는 증폭 될 외부 신호에 의해 여기됩니다. 이 신호에는 공동이 공명 할 수있는 주파수가 있어야합니다. 이 동축 케이블의 전류는 전기장이 발생하는 자기장을 설정합니다.
Klystron의 작업
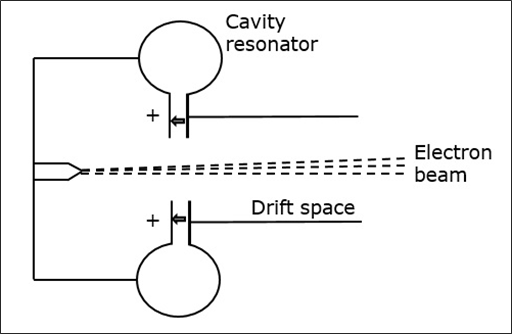
첫 번째 캐비티에 들어가는 전자 빔의 변조를 이해하기 위해 전기장을 고려해 봅시다. 공진기의 전기장은 유도장의 방향을 계속 변경합니다. 이것에 따라 전자총에서 나오는 전자는 속도를 제어합니다.
전자는 음전하를 띠기 때문에 전기장의 방향과 반대로 움직이면 가속됩니다. 또한 전자가 전기장의 같은 방향으로 움직이면 감속됩니다. 이 전기장은 계속 변하기 때문에 전자는 장의 변화에 따라 가속 및 감속됩니다. 다음 그림은 장이 반대 방향 일 때 전자 흐름을 나타냅니다.
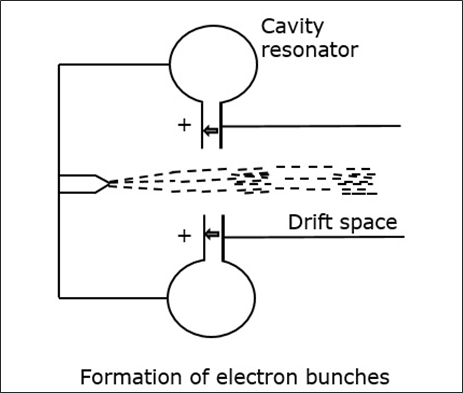
이동하는 동안 이러한 전자는 drift space다양한 속도로 공진기 사이에서 전자 다발을 생성합니다. 이 묶음은 이동 속도의 변화로 인해 생성됩니다.
이 묶음은 첫 번째 공진기가 진동하는 주파수에 해당하는 주파수로 두 번째 공진기로 들어갑니다. 모든 캐비티 공진기가 동일하기 때문에 전자의 움직임으로 인해 두 번째 공진기가 진동합니다. 다음 그림은 전자 다발의 형성을 보여줍니다.
두 번째 공진기에서 유도 된 자기장은 동축 케이블에 약간의 전류를 유도하여 출력 신호를 시작합니다. 두 번째 공동에있는 전자의 운동 에너지는 첫 번째 공동에있는 전자의 운동 에너지와 거의 동일하므로 공동에서 에너지를 가져 오지 않습니다.
전자는 두 번째 공동을 통과하는 동안 가속되는 반면 전자 다발이 감속됩니다. 따라서 모든 운동 에너지는 전자기 에너지로 변환되어 출력 신호를 생성합니다.
이러한 2- 캐비티 Klystron의 증폭은 낮으므로 다중 캐비티 Klystron이 사용됩니다.
다음 그림은 다중 캐비티 Klystron 증폭기의 예를 보여줍니다.
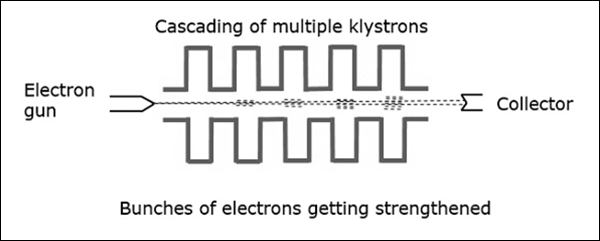
첫 번째 캐비티에 신호가 적용되면 두 번째 캐비티에서 약한 묶음이 생깁니다. 이것들은 세 번째 캐비티에 필드를 설정하여 더 집중된 뭉치를 생성합니다. 따라서 증폭이 더 큽니다.
이 마이크로파 발생기는 가변 주파수를 갖는 단일 공동에서 반사 및 진동에 대해 작동하는 Klystron입니다.
Reflex Klystron은 전자총, 음극 필라멘트, 양극 캐비티 및 음극 전위의 전극으로 구성됩니다. 저전력을 제공하고 효율성이 낮습니다.
Reflex Klystron의 건설
전자총은 양극 캐비티의 틈을 통과하는 전자빔을 방출합니다. 이 전자는 음전위가 높은 Repeller 전극으로 이동합니다. 높은 음의 장으로 인해 전자는 양극 캐비티로 다시 반발합니다. 돌아 오는 여정에서 전자는 갭에 더 많은 에너지를 제공하고 이러한 진동이 지속됩니다. 이 반사 클라이스트론의 구조적 세부 사항은 다음 그림과 같습니다.
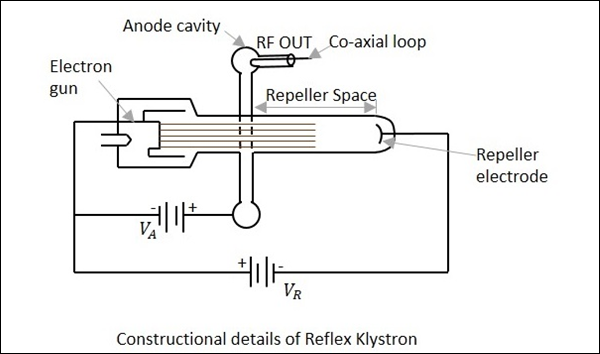
진동은 이미 튜브에 존재하고 작동에 의해 유지된다고 가정합니다. 양극 공동을 통과하는 동안 전자는 약간의 속도를 얻습니다.
Reflex Klystron의 작동
Reflex Klystron의 작동은 몇 가지 가정으로 이해됩니다. 전자빔은 양극 캐비티쪽으로 가속됩니다.
기준 전자가 er애노드 캐비티를 가로 지르지 만 추가 속도가 없으며 동일한 속도로 Repeller 전극에 도달 한 후 다시 반발합니다. 또 다른 전자,ee 이 기준 전자보다 일찍 시작된 것은 먼저 리 펠러에 도달하지만 천천히 돌아와 기준 전자와 동시에 도달합니다.
우리는 또 다른 전자를 가지고 있습니다. el, 둘 다 이후에 시작 er 과 ee그러나 er 및 ee와 동시에 도달하면서 되돌아 가면서 더 빠른 속도로 이동합니다.
자,이 세 개의 전자, 즉 er, ee 과 el 동시에 간격에 도달하여 electron bunch. 이 여행 시간을transit time, 최적의 값을 가져야합니다. 다음 그림은이를 보여줍니다.

양극 캐비티는 이동하는 동안 전자를 가속화하고 반환 여행 중에 전자를 지연시켜 에너지를 얻습니다. 갭 전압이 최대 양수이면 최대 음의 전자가 지연됩니다.
최적의 운송 시간은 다음과 같이 표시됩니다.
$$ T = n + \ frac {3} {4} \ quad 여기서 \ : n \ :은 \ : an \ : integer $$입니다.
이 이동 시간은 Repeller 및 양극 전압에 따라 다릅니다.
Reflex Klystron의 응용
Reflex Klystron은 다음과 같이 가변 주파수가 바람직한 응용 분야에 사용됩니다.
- 라디오 수신기
- 휴대용 마이크로파 링크
- 파라 메트릭 증폭기
- 마이크로파 수신기의 국부 발진기
- 마이크로파 발생기에서 가변 주파수가 바람직한 신호 소스로 사용됩니다.
이동 파 튜브는 Klystrons와 같은 공동 공진기가없는 광대역 마이크로파 장치입니다. 증폭은 전자빔과 무선 주파수 (RF) 장 사이의 장기간 상호 작용을 통해 이루어집니다.
Traveling Wave Tube의 구조
이동 파동 관은 음극관의 전자총을 포함하는 원통형 구조입니다. 양극판, 나선 및 수집기가 있습니다. RF 입력은 나선의 한쪽 끝으로 전송되고 출력은 나선의 다른 쪽 끝에서 가져옵니다.
전자총은 빛의 속도로 전자빔을 집중시킵니다. 자기장은 산란없이 빔이 초점을 맞추도록 안내합니다. RF 필드는 또한 나선에 의해 지연되는 빛의 속도로 전파됩니다. 나선은 느린 파도 구조로 작동합니다. 나선으로 전파되는인가 된 RF 장은 나선의 중심에 전기장을 생성합니다.
적용된 RF 신호로 인해 발생하는 전기장은 나선 원주에 대한 나선 피치의 비율을 곱한 빛의 속도와 함께 이동합니다. 나선을 통해 이동하는 전자 빔의 속도는 나선의 RF 파에 에너지를 유도합니다.
다음 그림은 진행파 튜브의 구조적 특징을 설명합니다.

따라서 증폭 된 출력은 TWT의 출력에서 얻어집니다. 축 위상 속도 $ V_p $는 다음과 같이 표현됩니다.
$$ V_p = V_c \ left ({Pitch} / {2 \ pi r} \ right) $$
어디 r나선의 반지름입니다. 나선은 $ V_p $ 위상 속도의 변화가 가장 적기 때문에 TWT에 대한 다른 느린 파도 구조보다 선호됩니다. TWT에서 전자총은 양극판 사이의 틈에있는 전자빔을 나선에 집중시킨 다음 수집기에서 수집합니다. 다음 그림은 진행파 튜브의 전극 배열을 설명합니다.
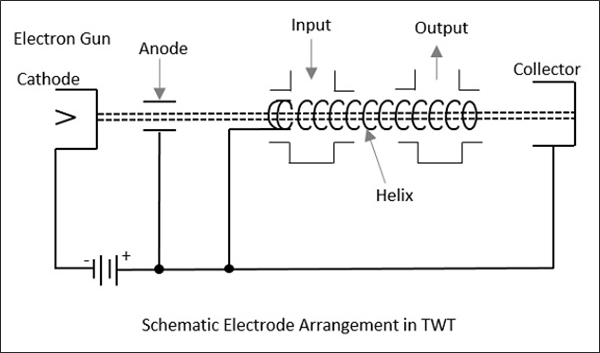
Traveling Wave Tube의 작동
양극판은 전위가 0 일 때, 즉 축 전기장이 노드에있을 때 전자빔 속도는 영향을받지 않습니다. 축 전기장의 파동이 양의 안티 노드에있을 때 전자 빔의 전자는 반대 방향으로 이동합니다. 가속되는이 전자는 RF 축장의 노드를 만나는 후기 전자를 따라 잡으려고합니다.
RF 축 방향 장이 음의 안티 노드에있는 지점에서 앞에서 언급 한 전자는 음의 전계 효과로 인해 추월하려고합니다. 전자는 변조 된 속도를받습니다. 누적 결과로 나선에서 두 번째 파동이 유도됩니다. 출력이 입력보다 커지고 결과적으로 증폭됩니다.
Traveling Wave Tube의 응용
진행파 튜브에는 많은 응용 분야가 있습니다.
TWT는 마이크로파 수신기에서 저잡음 RF 증폭기로 사용됩니다.
TWT는 또한 광대역 통신 링크 및 동축 케이블에서 중계기 증폭기 또는 중간 증폭기로 낮은 신호를 증폭하는 데 사용됩니다.
TWT는 튜브 수명이 길기 때문에 통신 위성에서 전원 출력 튜브로 사용됩니다.
연속파 고전력 TWT는 큰 전력과 큰 대역폭으로 인해 Troposcatter 링크에 사용되어 먼 거리로 분산됩니다.
TWT는 고출력 펄스 레이더 및 지상 기반 레이더에 사용됩니다.
지금까지 논의 된 튜브와 달리 마그네트론은 전기장과 자기장이 교차하는 교차 장 튜브입니다. 즉, 서로 수직으로 실행됩니다. TWT에서 전자가 Klystron에서보다 더 오랜 시간 동안 RF와 상호 작용할 때 더 높은 효율을 가져 오는 것으로 관찰되었습니다. 마그네트론에서도 동일한 기술을 따릅니다.
마그네트론의 유형
마그네트론에는 세 가지 주요 유형이 있습니다.
부정적인 저항 유형
- 두 양극 세그먼트 사이의 음의 저항이 사용됩니다.
- 효율성이 낮습니다.
- 저주파 (<500MHz)에서 사용됩니다.
사이클로트론 주파수 마그네트론
전기 부품과 진동하는 전자 사이의 동기화가 고려됩니다.
100MHz 이상의 주파수에 유용합니다.
이동 파 또는 공동 유형
전자와 회전하는 EM 장 사이의 상호 작용이 고려됩니다.
높은 피크 전력 진동이 제공됩니다.
레이더 애플리케이션에 유용합니다.
캐비티 마그네트론
마그네트론은 양극이 공진 캐비티로 만들어지고 영구 자석이 강력한 자기장을 생성하는 데 사용되기 때문에 캐비티 마그네트론이라고 불립니다.이 두 가지 작용으로 장치가 작동합니다.
캐비티 마그네트론의 건설
두꺼운 원통형 음극이 중앙에 있고 원통형 구리 블록이 축 방향으로 고정되어 양극 역할을합니다. 이 양극 블록은 공진 양극 공동 역할을하는 여러 슬롯으로 구성됩니다.
양극과 음극 사이에 존재하는 공간을 Interaction space. 전기장은 방사형으로 존재하는 반면 자기장은 캐비티 마그네트론에서 축 방향으로 존재합니다. 이 자기장은 영구 자석에 의해 생성되며, 자석 라인이 음극과 평행하고 양극과 음극 사이에 존재하는 전기장에 수직이되도록 배치됩니다.
다음 그림은 캐비티 마그네트론의 구조적 세부 사항과 축 방향으로 존재하는 자속의 자선을 보여줍니다.

이 캐비티 마그네트론에는 서로 단단히 결합 된 8 개의 캐비티가 있습니다. N 캐비티 마그네트론에는 $ N $ 작동 모드가 있습니다. 이러한 작업은 진동의 주파수와 위상에 따라 달라집니다. 이 캐비티 공진기의 링 주변의 총 위상 편이는 $ 2n \ pi $이어야합니다. 여기서 $ n $는 정수입니다.
$ \ phi_v $가 인접한 공동에 걸친 AC 전기장의 상대적 위상 변화를 나타내는 경우
$$ \ phi_v = \ frac {2 \ pi n} {N} $$
여기서 $ n = 0, \ : \ pm1, \ : \ pm2, \ : \ pm \ : (\ frac {N} {2} -1), \ : \ pm \ frac {N} {2} $
즉, $ N $가 짝수이면 $ \ frac {N} {2} $ 공명 모드가 존재할 수 있습니다.
만약,
$$ n = \ frac {N} {2} \ quad 다음 \ quad \ phi_v = \ pi $$
이 공명 모드를 $ \ pi-mode $라고합니다.
$$ n = 0 \ quad 다음 \ quad \ phi_v = 0 $$
이것은 Zero mode, 양극과 음극 사이에 RF 전기장이 없기 때문입니다. 이것은 또한Fringing Field 이 모드는 마그네트론에서 사용되지 않습니다.
캐비티 마그네트론의 작동
Cavity Klystron이 작동 중일 때 고려해야 할 다른 사례가 있습니다. 자세히 살펴 보겠습니다.
Case 1
자기장이 없으면, 즉 B = 0이면 다음 그림에서 전자의 거동을 관찰 할 수 있습니다. 예를 들어 전자가a 방사형 전기력 하에서 직접 양극으로 이동합니다.
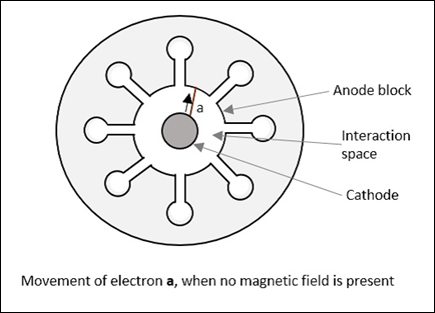
Case 2
자기장이 증가하면 횡력이 전자에 작용합니다. 이것은 전자를 고려할 때 다음 그림에서 볼 수 있습니다.b 두 힘이 작용하는 동안 곡선 경로를 사용합니다.

이 경로의 반경은 다음과 같이 계산됩니다.
$$ R = \ frac {mv} {eB} $$
그것은 전자의 속도에 비례하여 변하며 자기장 강도에 반비례합니다.
Case 3
자기장이 B 더 증가하면 전자는 전자와 같은 경로를 따릅니다. c, 양극 표면을 방목하고 양극 전류를 0으로 만듭니다. 이것을 "Critical magnetic field"$ (B_c) $는 차단 자기장입니다. 이해를 돕기 위해 다음 그림을 참조하십시오.
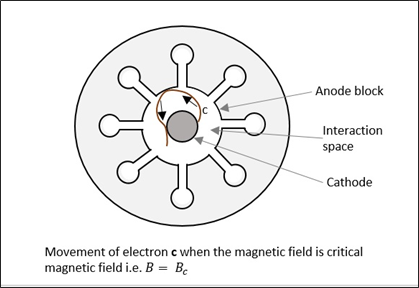
Case 4
자기장이 임계 장보다 커지면
$$ B> B_c $$
그런 다음 전자는 전자로 경로를 따라 d, 전자가 양극으로 가지 않고 음극으로 다시 점프합니다. 이로 인해 "back heating다음 그림을 참조하십시오.
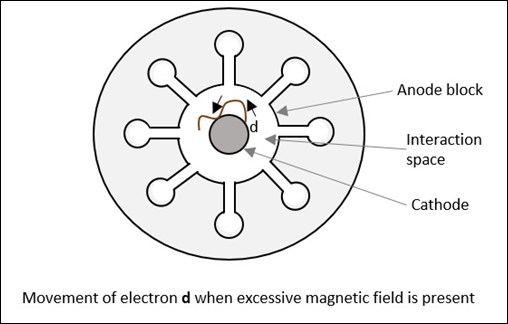
이것은 진동이 시작되면 전기 공급을 차단함으로써 달성됩니다. 이것이 계속되면 음극의 방출 효율이 영향을받습니다.
활성 RF 필드가있는 캐비티 마그네트론의 작동
지금까지 마그네트론의 공동 (정적 케이스)에 RF 필드가없는 공동 마그네트론의 작동에 대해 논의했습니다. 이제 활성 RF 필드가있을 때 작동에 대해 설명하겠습니다.
TWT에서와 같이 약간의 과도 잡음으로 인해 초기 RF 발진이 존재한다고 가정 해 보겠습니다. 진동은 장치의 작동에 의해 유지됩니다. 이 과정에서 방출되는 전자에는 세 종류가 있으며, 그 작용은 전자로 이해됩니다.a, b 과 c, 세 가지 다른 경우.
Case 1
진동이 존재하면 전자 a, 진동하는 에너지 전달 속도를 늦 춥니 다. 에너지를 진동으로 전달하는 이러한 전자를favored electrons. 이 전자는bunching effect.
Case 2
이 경우 다른 전자는 b, 진동에서 에너지를 가져와 속도를 증가시킵니다. 이 작업이 완료되면
- 더 날카롭게 구부러집니다.
- 상호 작용 공간에서 시간을 거의 소비하지 않습니다.
- 그것은 음극으로 돌아갑니다.
이 전자들은 unfavored electrons. 그들은 번칭 효과에 참여하지 않습니다. 또한 이러한 전자는 "역열"을 유발하므로 유해합니다.
Case 3
이 경우 전자 c조금 늦게 방출되는은 더 빠르게 이동합니다. 전자를 따라 잡으려고합니다a. 다음 방출 된 전자d, 단계적 시도 a. 결과적으로 선호되는 전자는a, c 과 d전자 다발 또는 전자 구름을 형성합니다. 이를 "위상 초점 효과"라고합니다.
이 전체 프로세스는 다음 그림을 보면 더 잘 이해됩니다.

그림 A는 다른 경우의 전자 이동을 보여주고 그림 B는 형성된 전자 구름을 보여줍니다. 이러한 전자 구름은 장치가 작동하는 동안 발생합니다. 이러한 양극 세그먼트의 내부 표면에 존재하는 전하는 공동의 진동을 따릅니다. 이것은 시계 방향으로 회전하는 전기장을 생성하여 실제 실험을 수행하는 동안 실제로 볼 수 있습니다.
전기장이 회전하는 동안 자속 선은 음극과 평행하게 형성되며, 그 결합 효과 아래에서 전자 다발은 나선형 궤적에서 가장 가까운 양의 양극 세그먼트로 일정한 간격으로 향하는 4 개의 스포크로 형성됩니다.
극초단파 측정기 중 극초단파 기기로 구성된 마이크로 웨이브 벤치의 설정이 눈에 띕니다. 이 전체 설정은 몇 번의 번갈아 가며 가이드 파장, 자유 공간 파장, 차단 파장, 임피던스, 주파수, VSWR, Klystron 특성, Gunn 다이오드 특성, 전력 측정 등과 같은 많은 값을 측정 할 수 있습니다.
전력을 결정할 때 마이크로파에 의해 생성되는 출력은 일반적으로 약간의 가치가 있습니다. 전송 라인의 위치에 따라 다릅니다. 일반적으로 마이크로파 벤치 설정이 될 마이크로파 전력을 측정하는 장비가 있어야합니다.
마이크로 웨이브 벤치 일반 측정 설정
이 설정은 자세히 관찰 할 수있는 여러 부분의 조합입니다. 다음 그림은 설정을 명확하게 설명합니다.

신호 발생기
이름에서 알 수 있듯이 몇 밀리 와트 정도의 마이크로파 신호를 생성합니다. 이것은 속도 변조 기술을 사용하여 연속파 빔을 밀리 와트 전력으로 전송합니다.
Gunn 다이오드 발진기 또는 Reflex Klystron 튜브가이 마이크로파 신호 발생기의 예가 될 수 있습니다.
정밀 감쇠기
원하는 주파수를 선택하고 출력을 0 ~ 50db로 제한하는 감쇠기입니다. 이것은 가변적이며 요구 사항에 따라 조정할 수 있습니다.
가변 감쇠기
이 감쇠기는 감쇠량을 설정합니다. 정밀 감쇠기의 값과 비교하여 판독 값을 확인하는 값의 미세 조정으로 이해할 수 있습니다.
아이솔레이터
이렇게하면 감지기 마운트에 도달하는 데 필요하지 않은 신호가 제거됩니다. 아이솔레이터를 사용하면 신호가 한 방향으로 만 도파관을 통과 할 수 있습니다.
주파수 측정기
이것은 신호의 주파수를 측정하는 장치입니다. 이 주파수 측정기를 사용하면 신호를 공진 주파수로 조정할 수 있습니다. 또한 신호를 도파관에 연결하는 기능을 제공합니다.
크리스탈 검출기
크리스탈 검출기 프로브 및 크리스탈 검출기 마운트는 위 그림에 표시되어 있으며 검출기는 프로브를 통해 마운트에 연결됩니다. 이것은 신호를 복조하는 데 사용됩니다.
정재파 표시기
정재파 전압계는 dB 단위의 정재파 비율 판독 값을 제공합니다. 도파관은 신호의 클럭 사이클을 조정하기 위해 약간의 간격으로 슬롯이 있습니다. 도파관으로 전송 된 신호는 BNC 케이블을 통해 VSWR 또는 CRO로 전달되어 특성을 측정합니다.
실시간 애플리케이션으로 설정된 마이크로파 벤치는 다음과 같습니다.

이제이 마이크로파 벤치의 중요한 부분 인 슬롯 형 라인을 살펴 보겠습니다.
슬롯 라인
마이크로파 전송 라인 또는 도파관에서 전자기장은 발생기에서 발생하는 입사 파와 발생기로 전달되는 반사파의 합으로 간주됩니다. 반사는 불일치 또는 불연속성을 나타냅니다. 반사파의 크기와 위상은 반사 임피던스의 진폭과 위상에 따라 달라집니다.
얻은 정상파는 효과적인 전송을 위해 임피던스 불일치에 대한 지식을 갖기 위해 필요한 전송 라인 결함을 알기 위해 측정됩니다. 이 슬롯 라인은 마이크로파 장치의 정재파 비율을 측정하는 데 도움이됩니다.
구성
슬롯 라인은 측정이 수행되어야하는 전송 라인의 슬롯 섹션으로 구성됩니다. 프로브를 필요할 때마다 연결할 수있는 이동식 프로브 캐리지와 기기를 부착하고 감지하는 기능이 있습니다.
도파관에서 슬롯은 넓은 측면의 중앙에 축 방향으로 만들어집니다. 크리스탈 검출기에 연결된 이동식 프로브가 도파관의 슬롯에 삽입됩니다.
조작
크리스탈 검출기의 출력은 적용된 입력 전압의 제곱에 비례합니다. 이동식 프로브를 사용하면 해당 위치에서 편리하고 정확한 측정이 가능합니다. 그러나 프로브가 이동함에 따라 출력은 도파관 내부에 형성된 정상파 패턴에 비례합니다. 정확한 결과를 얻기 위해 가변 감쇠기가 여기에 사용됩니다.
출력 VSWR은 다음과 같이 얻을 수 있습니다.
$$ VSWR = \ sqrt {\ frac {V_ {max}} {V_ {min}}} $$
여기서 $ V $는 출력 전압입니다.
다음 그림은 레이블이 지정된 슬롯 라인의 여러 부분을 보여줍니다.

위 그림에 표시된 부품은 다음을 나타냅니다.
- Launcher-신호를 초대합니다.
- 도파관의 더 작은 섹션.
- Isolator-소스에 대한 반사를 방지합니다.
- 회전식 가변 감쇠기-미세 조정용.
- 슬롯 섹션-신호를 측정합니다.
- 프로브 깊이 조정.
- 조정 조정-정확도를 얻으려면.
- 크리스탈 검출기-신호를 감지합니다.
- Matched load-나가는 힘을 흡수합니다.
- 단락-부하로 교체 할 준비.
- 회전 노브-측정하는 동안 조정합니다.
- 버니어 게이지-정확한 결과를 위해.
오실로스코프에서 저주파 변조 신호를 얻기 위해 조정 가능한 검출기가있는 슬롯 라인이 사용됩니다. 조정 가능한 감지기가있는 슬롯 형 라인 캐리지는 다음을 측정하는 데 사용할 수 있습니다.
- VSWR (전압 정재파 비율)
- 정재파 패턴
- Impedance
- 반사 계수
- 반사 손실
- 사용 된 발전기의 주파수
조정 가능한 감지기
조정 가능 감지기는 저주파 구형파 변조 마이크로파 신호를 감지하는 데 사용되는 감지기 마운트입니다. 다음 그림은 조정 가능한 감지기 마운트에 대한 아이디어를 제공합니다.
다음 이미지는이 장치의 실제 적용을 나타냅니다. 끝이 끝나고 위와 같이 다른 쪽 끝에 구멍이 있습니다.

마이크로파 전송 시스템과 검출기 마운트 간의 일치를 제공하기 위해 조정 가능한 스터브가 자주 사용됩니다. 튜너 블 스텁에는 세 가지 유형이 있습니다.
- 조정 가능한 도파관 감지기
- 조정 가능한 동축 감지기
- 조정 가능한 프로브 감지기
또한 다음과 같은 고정 스텁이 있습니다.
- 고정 광대역 튜닝 프로브
- 고정 도파관 일치 감지기 마운트
검출기 마운트는 끝에서 종료되는 마이크로 웨이브 벤치의 마지막 단계입니다.
마이크로 웨이브 엔지니어링 분야에서는 이미 첫 번째 장에서 언급했듯이 많은 응용 분야가 발생합니다. 따라서 다양한 애플리케이션을 사용하는 동안 효과적인 사용을 위해 전력, 감쇠, 위상 편이, VSWR, 임피던스 등과 같은 다양한 값을 측정해야하는 경우가 종종 있습니다.
이 장에서는 다양한 측정 기술을 살펴 보겠습니다.
전력 측정
측정 된 마이크로파 전력은 도파관의 모든 위치에서 평균 전력입니다. 전력 측정은 세 가지 유형이 있습니다.
-
저전력 측정 (0.01mW ~ 10mW)
예-부피 측정 기법
-
중전 력 측정 (10mW ~ 1W)
예-열량계 기술
-
고전력 측정 (> 10W)
예-열량계 전력계
자세히 살펴 보겠습니다.
저전력 측정
0.01mW ~ 10mW의 마이크로파 전력 측정은 저전력 측정으로 이해할 수 있습니다.
Bolometer낮은 마이크로파 전력 측정에 사용되는 장치입니다. 볼로미터에 사용되는 요소는 양 또는 음의 온도 계수 일 수 있습니다. 예를 들어, barrater는 온도가 증가함에 따라 저항이 증가하는 양의 온도 계수를 갖습니다. 서미스터는 온도가 증가함에 따라 저항이 감소하는 음의 온도 계수를 갖습니다.
볼로미터에는 어느 것이나 사용할 수 있지만 저항의 변화는 측정에 적용되는 마이크로파 전력에 비례합니다. 이 볼로미터는 팔 다리에서 하나로 사용되어 불균형이 발생하여 출력에 영향을 미칩니다. 볼로미터를 사용하는 브리지 회로의 일반적인 예는 다음 그림과 같습니다.
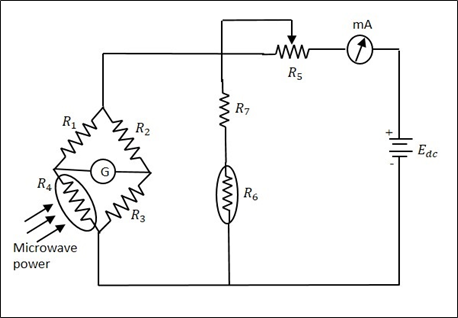
여기서 밀리미터는 흐르는 전류의 값을 나타냅니다. 배터리는 가변적이며 볼로미터의 동작으로 인해 불균형이 발생할 때 균형을 얻기 위해 변경됩니다. DC 배터리 전압에서 이루어지는이 조정은 마이크로파 전력에 비례합니다. 이 회로의 전력 처리 용량은 제한되어 있습니다.
중 출력 측정
10mW에서 1W 정도의 마이크로파 전력 측정은 중간 전력의 측정으로 이해 될 수 있습니다.
일반적으로 특정 값의 비열을 유지하는 특수 부하가 사용됩니다. 측정 할 전력은 이미 유지하고있는 부하의 출력 온도를 비례 적으로 변경하는 입력에 적용됩니다. 온도 상승의 차이는 부하에 대한 입력 마이크로파 전력을 지정합니다.
브리지 균형 기술은 여기에서 출력을 얻는 데 사용됩니다. 열 전달 방법은 열량 측정 기술인 전력 측정에 사용됩니다.
고출력 측정
10W ~ 50KW 주변의 마이크로파 전력 측정은 고전력 측정으로 이해 될 수 있습니다.
높은 마이크로파 전력은 일반적으로 건식 및 흐름 유형일 수있는 열량계 전력계로 측정됩니다. 건식 타입은 히스테리시스 손실이 높은 유전체로 채워진 동축 케이블을 사용하여 명명 된 반면, 플로우 타입은 마이크로파 흡수에 좋은 물이나 기름 또는 액체를 사용하여 명명되었습니다.
부하에 들어가기 전과 후의 액체 온도 변화는 값 교정을 위해 사용됩니다. 이 방법의 한계는 유량 결정, 교정 및 열 관성 등과 같습니다.
감쇠 측정
실제로 마이크로파 구성 요소 및 장치는 종종 약간의 감쇠를 제공합니다. 제공되는 감쇠량은 두 가지 방법으로 측정 할 수 있습니다. 그들은-전력비 방법 및 RF 대체 방법입니다.
감쇠는 입력 전력 대 출력 전력의 비율이며 일반적으로 데시벨로 표시됩니다.
$$ 감쇠 \ : in \ : dBs = 10 \ : log \ frac {P_ {in}} {P_ {out}} $$
$ P_ {in} $ = 입력 전력, $ P_ {out} $ = 출력 전력
전력비 방법
이 방법에서 감쇠 측정은 두 단계로 이루어집니다.
Step 1 − 전체 마이크로 웨이브 벤치의 입력 및 출력 전력은 감쇠를 계산해야하는 장치없이 수행됩니다.
Step 2 − 전체 마이크로 웨이브 벤치의 입력 및 출력 전력은 감쇠를 계산해야하는 장치로 수행됩니다.
비교했을 때 이러한 전력의 비율은 감쇠 값을 제공합니다.
다음 그림은이를 설명하는 두 가지 설정입니다.

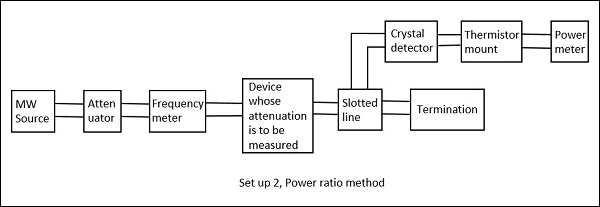
Drawback − 입력 전력이 낮고 네트워크 감쇠가 큰 경우 전력 및 감쇠 측정이 정확하지 않을 수 있습니다.
RF 대체 방법
이 방법에서는 감쇠 측정이 세 단계로 이루어집니다.
Step 1 − 전체 마이크로 웨이브 벤치의 출력 전력은 감쇠를 계산해야하는 네트워크로 측정됩니다.
Step 2 − 전체 Microwave 벤치의 출력 전력은 네트워크를 정밀 보정 된 감쇠기로 교체하여 측정됩니다.
Step 3 − 이제이 감쇠기는 네트워크로 측정 된 것과 동일한 전력을 얻도록 조정됩니다.
다음 그림은이를 설명하는 두 가지 설정입니다.
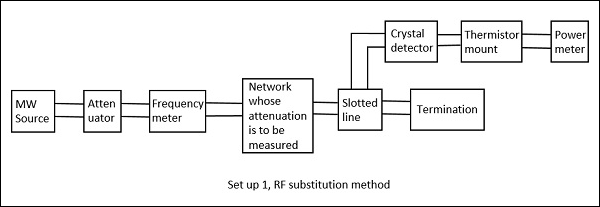
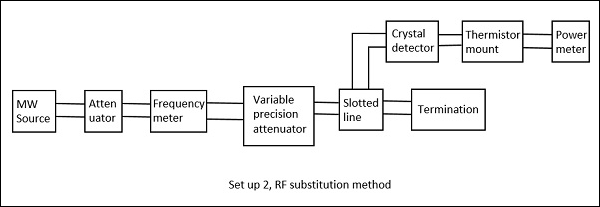
감쇠기의 조정 된 값은 네트워크의 감쇠를 직접 제공합니다. 위 방법의 단점은 여기서 피할 수 있으므로 감쇠를 측정하는 더 좋은 절차입니다.
위상 편이 측정
실제 작업 조건에서 실제 신호에서 신호의 위상 변화가 발생할 수 있습니다. 이러한 위상 편이를 측정하기 위해 우리는 위상 편이를 보정 할 수있는 비교 기법을 사용합니다.
위상 편이를 계산하기위한 설정은 다음 그림에 나와 있습니다.
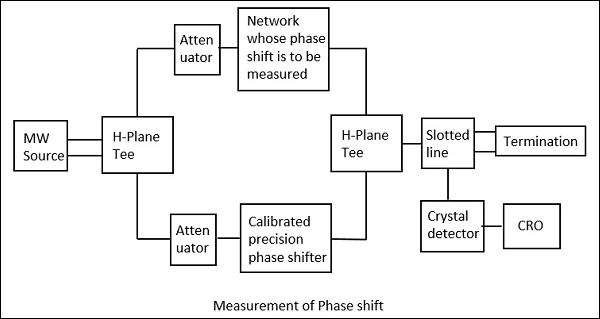
여기에서 마이크로파 소스가 신호를 생성 한 후에는 한 포트가 위상 편이를 측정 할 네트워크에 연결되고 다른 포트가 조정 가능한 정밀 위상 시프터에 연결되는 H- 평면 Tee 접합을 통과합니다.
복조 된 출력은 연결된 CRO에서 관찰되는 1KHz 사인파입니다. 이 위상 시프터는 1KHz 사인파의 출력도 위와 일치하도록 조정됩니다. 듀얼 모드 CRO에서 관찰하여 매칭이 완료된 후이 정밀 위상 시프터는 위상 시프트를 판독합니다. 이것은 다음 그림에서 명확하게 이해됩니다.
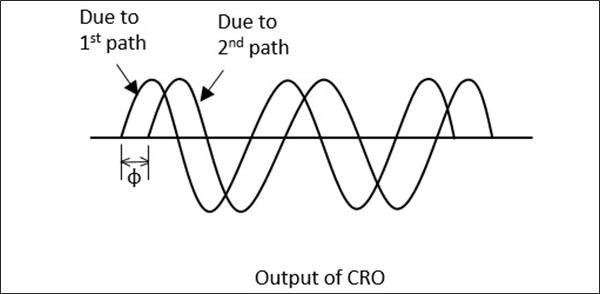
이 절차는 위상 편이 측정에 가장 많이 사용되는 절차입니다. 이제 VSWR을 계산하는 방법을 살펴 보겠습니다.
VSWR 측정
모든 Microwave 실제 응용 분야에서 모든 종류의 임피던스 불일치는 정상파의 형성으로 이어집니다. 이러한 정상파의 강도는 전압 정상파 비율 ($ VSWR $)로 측정됩니다. 최대 전압과 최소 전압의 비율은 $ VSWR $를 제공하며 $ S $로 표시됩니다.
$$ S = \ frac {V_ {max}} {V_ {min}} = \ frac {1+ \ rho} {1- \ rho} $$
여기서 $ \ rho = 반사 \ : co-효율적 = \ frac {P_ {reflected}} {P_ {incident}} $
$ VSWR $의 측정은 Low $ VSWR $ 및 High $ VSWR $ 측정의 두 가지 방법으로 수행 할 수 있습니다.
낮은 VSWR 측정 (S <10)
낮은 $ VSWR $의 측정은 감쇠기를 조정하여 VSWR 미터 인 DC 밀리 볼트 미터에서 판독 값을 얻을 수 있습니다. DC 밀리 볼트 미터가 최소 판독 값뿐 아니라 전체 스케일 판독 값을 표시하도록 슬롯 라인과 감쇠기를 조정하여 판독 값을 얻을 수 있습니다.
이제이 두 판독 값을 계산하여 네트워크의 $ VSWR $를 찾습니다.
높은 VSWR 측정 (S> 10)
값이 10보다 큰 높은 $ VSWR $의 측정은 다음과 같은 방법으로 측정 할 수 있습니다. double minimum method. 이 방법에서는 최소값의 판독 값을 취하고 문장 전과 후의 문장에서 최소값의 절반 지점에서 판독 값도 취합니다. 이것은 다음 그림으로 이해할 수 있습니다.
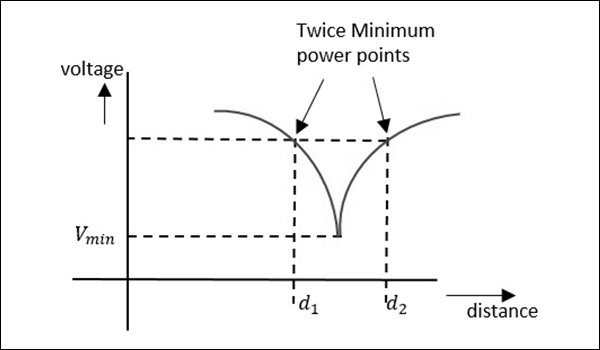
이제 $ VSWR $는 다음과 같은 관계식으로 계산할 수 있습니다.
$$ VSWR = \ frac {\ lambda_ {g}} {\ pi (d_2-d_1)} $$
여기서 $ \ lambda_g \ :는 \ : \ : 유도 된 \ : 파장 $입니다.
$$ \ lambda_g = \ frac {\ lambda_0} {\ sqrt {1-(\ frac {\ lambda_0} {\ lambda_c}) ^ 2}} \ quad 여기서 \ : \ lambda_0 \ : = {c} / {f} $$
여기서는 두 가지 최소 점을 고려하고 있으므로이를 이중 최소 방법이라고합니다. 이제 임피던스 측정에 대해 알아 보겠습니다.
임피던스 측정
Magic Tee 외에도 두 가지 방법이 있습니다. 하나는 슬롯 라인을 사용하는 것이고 다른 하나는 반사 계를 사용하는 것입니다.
슬롯 라인을 사용한 임피던스
이 방법에서는 슬롯 라인과 부하 $ Z_L $를 사용하여 임피던스를 측정하고이를 사용하여 $ V_ {max} $ 및 $ V_ {min} $를 결정할 수 있습니다. 이 방법에서는 임피던스 측정이 두 단계로 이루어집니다.
Step 1 − $ Z_L $ 부하를 사용하여 Vmin 결정.
Step 2 − 부하를 단락시켜 Vmin을 결정합니다.
이것은 다음 그림에 나와 있습니다.
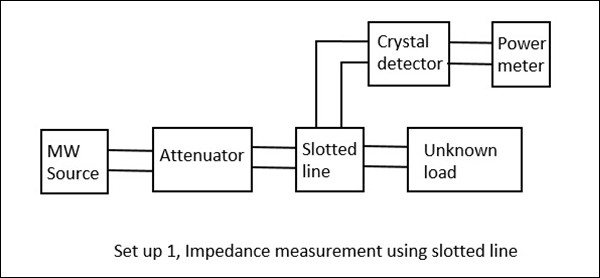
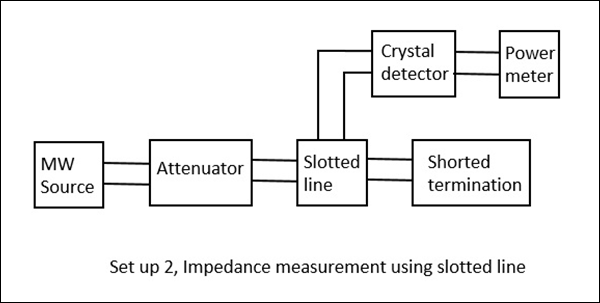
부하를 사용하여 $ V_ {max} $ 및 $ V_ {min} $의 값을 얻으려고하면 특정 값을 얻습니다. 그러나 부하를 단락시켜 동일한 작업을 수행하면 최소값이 오른쪽 또는 왼쪽으로 이동합니다. 이 이동이 왼쪽이면 부하가 유도 성임을 의미하고 오른쪽으로 이동하면 부하가 본질적으로 용량 성임을 의미합니다. 다음 그림은이를 설명합니다.
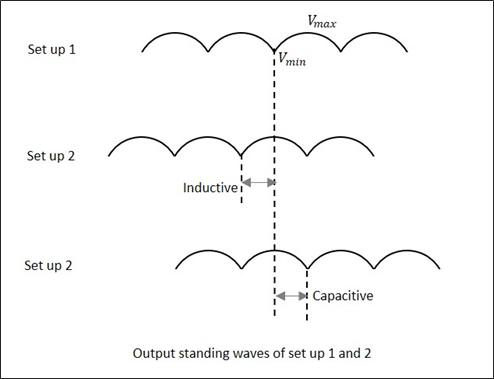
데이터를 기록하면 알 수없는 임피던스가 계산됩니다. 임피던스 및 반사 계수 $ \ rho $는 크기와 위상 모두에서 얻을 수 있습니다.
반사 계를 사용한 임피던스
슬롯 형 라인과 달리 반사 계는 위상 각이 아닌 임피던스의 크기 만 찾는 데 도움이됩니다. 이 방법에서는 동일하지만 방향이 다른 두 개의 방향성 커플러가 사용됩니다.
이 두 커플러는 부하에서 입사 전력 $ P_i $ 및 반사 전력 $ P_r $을 샘플링하는 데 사용됩니다. 반사 계는 다음 그림과 같이 연결됩니다. 임피던스를 구할 수있는 반사 계수 $ \ rho $의 크기를 구하는 데 사용됩니다.

반사 계 판독 값에서 우리는
$$ \ rho = \ sqrt {\ frac {P_r} {P_i}} $$
$ \ rho $의 값에서 $ VSWR $, 즉 $ S $와 임피던스는 다음과 같이 계산할 수 있습니다.
$$ S = \ frac {1+ \ rho} {1- \ rho} \ quad 및 \ quad \ frac {z-z_g} {z + z_g} = \ rho $$
여기서 $ z_g $는 알려진 파동 임피던스이고 $ z $는 알려지지 않은 임피던스입니다.
여기서는 순파 및 역파 매개 변수가 관찰되지만 커플러의 방향 특성으로 인해 간섭이 없습니다. 감쇠기는 낮은 입력 전력을 유지하는 데 도움이됩니다.
공동 공진기의 Q 측정
측정 방법은 Transmission 방식, Impedance 방식, Transient Decay 또는 Decrement 방식의 세 가지 방법이 있지만 Q 공동 공진기의 가장 쉽고 가장 많이 따르는 방법은 Transmission Method. 따라서 측정 설정을 살펴 보겠습니다.
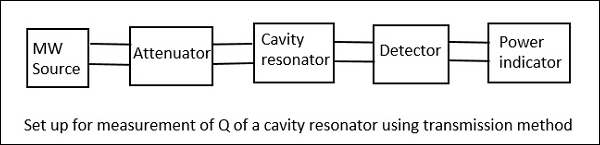
이 방법에서 공동 공진기는 전송하는 장치 역할을합니다. 출력 신호는 다음 그림과 같이 공진 곡선을 생성하는 주파수 함수로 표시됩니다.
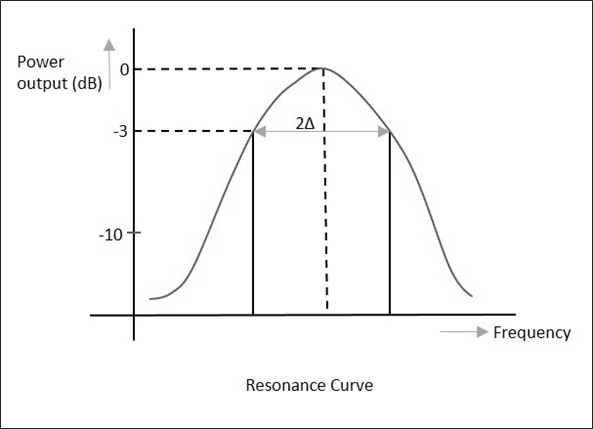
위의 설정에서 마이크로파 소스의 신호 주파수가 변경되어 신호 레벨을 일정하게 유지 한 다음 출력 전력을 측정합니다. 캐비티 공진기는이 주파수로 조정되고 신호 레벨과 출력 전력이 다시 기록되어 차이를 알 수 있습니다.
출력이 플로팅되면 공명 곡선이 얻어지며 여기서 HPBW (Half Power Bandwidth) $ (2 \ Delta) $ 값을 확인할 수 있습니다.
$$ 2 \ 델타 = \ pm \ frac {1} {Q_L} $$
여기서 $ Q_L $은로드 된 값입니다.
$$ 또는 \ quad Q_L = \ pm \ frac {1} {2 \ Delta} = \ pm \ frac {w} {2 (w-w_0)} $$
마이크로파 소스와 캐비티 간의 커플 링과 검출기와 캐비티 간의 커플 링이 무시되면
$$ Q_L = Q_0 \ : (언로드 됨 \ : Q) $$
약점
이 시스템의 가장 큰 단점은 좁은 작동 대역으로 인해 매우 높은 Q 시스템에서 정확도가 약간 떨어진다는 것입니다.
우리는 다양한 매개 변수에 대한 여러 유형의 측정 기술을 다루었습니다. 이제 이것에 대한 몇 가지 예제 문제를 해결해 보겠습니다.
이 장에서는 마이크로파와 관련된 몇 가지 수치 문제를 풀면서 재미를 보겠습니다.
문제 1
$ a = 5cm, b = 3cm $ 크기의 $ TE_ {10} $ 모드 도파관을 사용하는 전송 시스템은 10GHz. 두 개의 최소 전력 점 사이에서 측정 된 거리는 다음과 같습니다.1mm on a slotted line. Calculate the VSWR of the system.
해결책
$ f = 10GHz라고 가정하면; a = 5cm; b = 3cm $
$ TE_ {10} $ 모드 도파관의 경우
$$ \ lambda_c = 2a = 2 \ times 5 = 10cm $$
$$ \ lambda_0 = \ frac {c} {f} = \ frac {3 \ times10 ^ {10}} {10 \ times10 ^ 9} = 3cm $$
$$ d_2-d_1 = 1mm = 10 ^ {-1} cm $$
우린 알아
$$ \ lambda_g = \ frac {\ lambda_0} {1-({\ lambda_0} / {\ lambda_c}) ^ 2} = \ frac {3} {\ sqrt {1-({3} / {10}) ^ 2}} = 3.144cm $$
이중 최소 방법의 경우 VSWR은 다음과 같이 제공됩니다.
$$ VSWR = \ frac {\ lambda_g} {\ pi (d_2-d_1)} = \ frac {3.144} {\ pi (1 \ times10 ^ {-1})} = 10.003 = 10 $$
따라서 주어진 전송 시스템의 VSWR 값은 10입니다.
문제 2
반사 계의 임피던스 측정 설정에서 두 커플러의 출력이 다음과 같을 때 반사 계수는 얼마입니까? 2mw 과 0.5mw 각기?
해결책
을 고려하면
$$ \ frac {P_i} {100} = 2mw \ quad 및 \ quad \ frac {P_r} {100} = 0.5mw $$
$$ P_i = 2 \ times 100mw = 200mw $$
$$ P_r = 0.5 \ times 100mw = 50mw $$
$$ \ rho = \ sqrt {\ frac {P_r} {P_i}} = \ sqrt {\ frac {50mw} {200mw}} = \ sqrt {0.25} = 0.5 $$
따라서 주어진 설정의 반사 계수 $ \ rho $는 0.5입니다.
문제 3
두 개의 동일한 커플러가 도파관에 사용되어 입사 전력을 3mw로 샘플링하고 반사 전력을 0.25mw, $ VSWR $의 값을 찾으십시오.
해결책
우리는 알고 있습니다
$$ \ rho = \ sqrt {\ frac {P_r} {P_i}} = \ sqrt {\ frac {0.25} {3}} = \ sqrt {0.0833} = 0.288 $$
$$ VSWR = S = \ frac {1+ \ rho} {1- \ rho} = \ frac {1 + 0.288} {1-0.288} = \ frac {1.288} {0.712} = 1.80 $$
따라서 위 시스템의 $ VSWR $ 값은 1.80입니다.
문제 4
두 개의 동일한 30dB지향성 커플러는 도파관에서 입사 및 반사 전력을 샘플링하는 데 사용됩니다. VSWR의 값은 다음과 같습니다.6 커플러 샘플링 입사 전력의 출력은 5mw. 반사 된 전력의 가치는 무엇입니까?
해결책
우리는 알고 있습니다
$$ VSWR = S = \ frac {1+ \ rho} {1- \ rho} = 6 $$
$$ (1+ \ rho) = 6 (1- \ rho) = 6-6 \ rho $$
$$ 7 \ rho = 5 $$
$$ \ rho = \ frac {5} {7} = 0.174 $$
반사 된 전력의 가치를 얻기 위해
$$ \ rho = \ sqrt {\ frac {{P_r} / {10 ^ 3}} {{P_i} / {10 ^ 3}}} = \ sqrt {\ frac {P_r} {P_i}} $$
$$ 또는 \ quad \ rho ^ 2 = \ frac {P_r} {P_i} $$
$$ P_r = \ rho ^ 2.P_i = (0.714) ^ 2.5 = 0.510 \ times 5 = 2.55 $$
따라서이 도파관의 반사 전력은 2.55mW입니다.