TensorFlow-선형 회귀
이 장에서는 TensorFlow를 사용한 선형 회귀 구현의 기본 예제에 중점을 둘 것입니다. 로지스틱 회귀 또는 선형 회귀는 순서 불연속 범주의 분류를위한지도 머신 러닝 접근 방식입니다. 이 장의 목표는 사용자가 예측 변수와 하나 이상의 독립 변수 간의 관계를 예측할 수있는 모델을 구축하는 것입니다.
이 두 변수 사이의 관계는 선형으로 간주됩니다. y가 종속 변수이고 x가 독립 변수로 간주되면 두 변수의 선형 회귀 관계는 다음 방정식과 같습니다.
Y = Ax+b선형 회귀 알고리즘을 설계합니다. 이를 통해 다음 두 가지 중요한 개념을 이해할 수 있습니다.
- 비용 함수
- 경사 하강 법 알고리즘
선형 회귀의 개략적 표현은 아래에 언급되어 있습니다.

선형 회귀 방정식의 그래픽보기는 다음과 같습니다.
선형 회귀 알고리즘을 설계하는 단계
이제 선형 회귀 알고리즘을 설계하는 데 도움이되는 단계에 대해 알아 봅니다.
1 단계
선형 회귀 모듈을 그리는 데 필요한 모듈을 가져 오는 것이 중요합니다. Python 라이브러리 NumPy 및 Matplotlib 가져 오기를 시작합니다.
import numpy as np
import matplotlib.pyplot as plt2 단계
로지스틱 회귀에 필요한 계수 수를 정의합니다.
number_of_points = 500
x_point = []
y_point = []
a = 0.22
b = 0.783 단계
회귀 방정식 주위에 300 개의 임의의 점을 생성하기 위해 변수를 반복합니다.
Y = 0.22x + 0.78
for i in range(number_of_points):
x = np.random.normal(0.0,0.5)
y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x])
y_point.append([y])4 단계
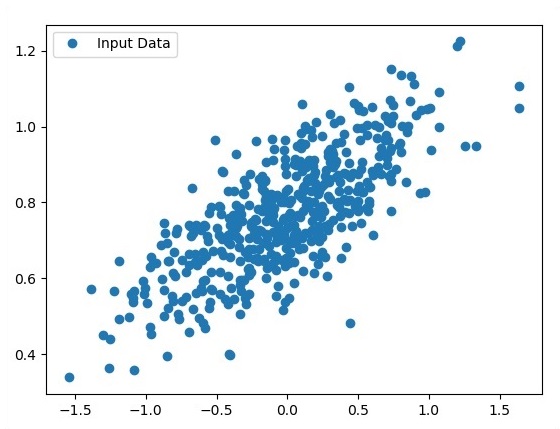
Matplotlib를 사용하여 생성 된 포인트를 봅니다.
fplt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() plt.show()로지스틱 회귀의 전체 코드는 다음과 같습니다.
import numpy as np
import matplotlib.pyplot as plt
number_of_points = 500
x_point = []
y_point = []
a = 0.22
b = 0.78
for i in range(number_of_points):
x = np.random.normal(0.0,0.5)
y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x])
y_point.append([y])
plt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend()
plt.show()입력으로 사용되는 점수는 입력 데이터로 간주됩니다.