Połączenia obwodów w kondensatorach
W obwodzie kondensator można podłączyć szeregowo lub równolegle. Jeśli zestaw kondensatorów był podłączony w obwodzie, rodzaj połączenia kondensatorów dotyczy wartości napięcia i prądu w tej sieci.
Kondensatory szeregowo
Zobaczmy, co się dzieje, gdy kilka kondensatorów jest połączonych szeregowo. Rozważmy trzy kondensatory o różnych wartościach, jak pokazano na poniższym rysunku.

Pojemność
Kiedy rozważana jest pojemność sieci, której kondensatory są połączone szeregowo, odwrotność pojemności wszystkich kondensatorów jest dodawana, aby uzyskać odwrotność całkowitej pojemności. Aby uzyskać to jaśniej,
$$ \ frac {1} {C_ {T}} \: \: = \: \: \ frac {1} {C_ {1}} \: \: + \: \: \ frac {1} {C_ { 2}} \: \: + \: \: \ frac {1} {C_ {3}} $$
Zgodnie z tym samym wzorem, jeśli tylko dwa kondensatory są połączone szeregowo, to
$$ C_ {T} \: \: = \: \: \ frac {C_ {1} \: \: \ times \: \: C_ {2}} {C_ {1} \: \: + \: \ : C_ {2}} $$
Gdzie C 1 ma pojemność przez 1 st kondensator C 2 ma pojemność przez 2 nd kondensator C 3 jest pojemność przez 3 rd kondensatora wyżej sieci.
Napięcie
Napięcie na każdym kondensatorze zależy od wartości poszczególnych pojemności. Co znaczy
$$ V_ {C1} \: \: = \: \: \ frac {Q_ {T}} {C_ {1}} \: \: V_ {C2} \: \: = \: \: \ frac {Q_ {T}} {C_ {2}} \: \: V_ {C3} \: \: = \: \: \ frac {Q_ {T}} {C_ {3}} $$
Całkowite napięcie w obwodzie kondensatorów szeregowych,
$$ V_ {T} \: \: = \: \: V_ {C1} \: \: + \: \: V_ {C2} \: \: + \: \: V_ {C3} $$
Gdzie V C1 jest napięcie na 1 st kondensatora, V C2 jest napięcie na 2 nd kondensatora i V C3 jest napięcie na 3 -ciej kondensatora wyżej sieci.
obecny
Całkowita ilość prądu przepływającego przez zestaw kondensatorów połączonych szeregowo jest taka sama we wszystkich punktach. Dlatego kondensatory będą przechowywać tę samą ilość ładunku niezależnie od ich wartości pojemności.
Prąd przez sieć,
$$ I \: \: = \: \: I_ {1} \: \: = \: \: I_ {2} \: \: = \: \: I_ {3} $$
Gdzie 1 jest obecny przez 1 st kondensatora I 2 jest obecny przez 2 nd kondensatora i 3 jest to prąd płynący przez 3 rd kondensatora wyżej sieci.
Ponieważ prąd jest taki sam, magazynowanie ładunku jest takie samo, ponieważ każda płytka kondensatora pobiera ładunek z sąsiedniego kondensatora, a zatem kondensatory połączone szeregowo będą miały ten sam ładunek.
$$ Q_ {T} \: \: = \: \: Q_ {1} \: \: = \: \: Q_ {2} \: \: = \: \: Q_ {3} $$
Kondensatory równolegle
Przyjrzyjmy się, co się dzieje, gdy kilka kondensatorów jest połączonych równolegle. Rozważmy trzy kondensatory o różnych wartościach, jak pokazano na poniższym rysunku.
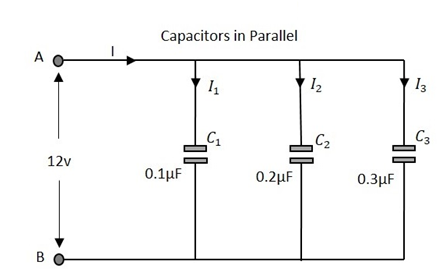
Pojemność
Całkowita pojemność obwodu jest odpowiednikiem sumy indywidualnych pojemności kondensatorów w sieci.
$$ C_ {T} \: \: = \: \: C_ {1} \: \: + \: \: C_ {2} \: \: + \: \: C_ {3} $$
Gdzie C 1 ma pojemność przez 1 st kondensator C 2 ma pojemność przez 2 nd kondensator C 3 jest pojemność przez 3 rd kondensatora wyżej sieci.
Napięcie
Napięcie zmierzone na końcu obwodu wynosi same jako napięcie na wszystkich kondensatorach połączonych równolegle.
$$ V_ {T} \: \: = \: \: V_ {1} \: \: = \: \: V_ {2} \: \: = \: \: V_ {3} $$
Gdzie V C1 jest napięcie na 1 st kondensatora, V C2 jest napięcie na 2 nd kondensatora i V C3 jest napięcie na 3 -ciej kondensatora wyżej sieci.
obecny
Całkowity przepływ prądu jest równy sumie prądów przepływających przez każdy kondensator podłączony w sieci równoległej.
$$ I_ {T} \: \: = \: \: I_ {1} \: \: + \: \: I_ {2} \: \: + \: \: I_ {3} $$
Gdzie 1 jest obecny przez 1 st kondensatora I 2 jest obecny przez 2 nd kondensatora i 3 jest to prąd płynący przez 3 rd kondensatora wyżej sieci.