Połączenia obwodów w cewkach
Cewka indukcyjna podłączona w obwodzie może być połączeniem szeregowym lub równoległym. Pozwól nam teraz wiedzieć, co się stanie z całkowitymi wartościami prądu, napięcia i rezystancji, jeśli są one również połączone szeregowo, gdy są połączone równolegle.
Cewki szeregowe
Przyjrzyjmy się, co się dzieje, gdy kilka cewek jest połączonych szeregowo. Rozważmy trzy rezystory o różnych wartościach, jak pokazano na poniższym rysunku.
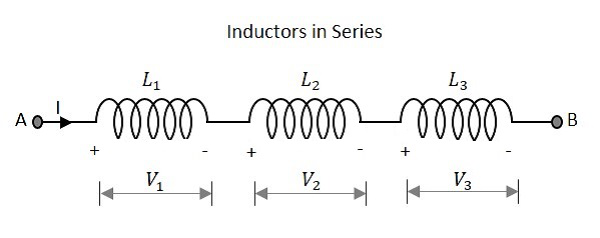
Indukcyjność
Całkowita indukcyjność obwodu z cewkami szeregowymi jest równa sumie poszczególnych indukcyjności. Całkowita wartość indukcyjności sieci podanej powyżej wynosi
$$ L_ {T} \: \: = \: \: L_ {1} \: \: + \: \: L_ {2} \: \: + \: \: L_ {3} $$
W którym L 1 jest indukcyjnością 1 st rezystor L 2 jest indukcyjnością 2 nd rezystora i L 3 jest indukcyjnością 3 rd rezystor wyżej sieci.
Napięcie
Całkowite napięcie, które pojawia się w szeregu cewek indukcyjnych, jest sumą spadków napięcia na każdej indywidualnej indukcyjności.
Całkowite napięcie, które pojawia się w obwodzie
$$ V \: \: = \: \: V_ {1} \: \: + \: \: V_ {2} \: \: + \: \: V_ {3} $$
Gdzie V 1 jest spadek napięcia na 1 st cewki V 2 jest spadek napięcia na 2 nd cewki i V 3 jest spadek napięcia na 3 -ciej induktor w powyższym sieci.
obecny
Całkowita ilość prądu przepływającego przez zestaw cewek połączonych szeregowo jest taka sama we wszystkich punktach w całej sieci.
Prąd przez sieć
$$ I \: \: = \: \: I_ {1} \: \: = \: \: I_ {2} \: \: = \: \: I_ {3} $$
Gdzie I 1 jest prądem płynącym przez pierwszą cewkę indukcyjną, Ja 2 jest prądem płynącym przez drugą cewkę indukcyjną, a Ja 3 jest prądem płynącym przez trzecią cewkę w powyższej sieci.
Induktory równoległe
Zobaczmy, co się dzieje, gdy kilka rezystorów jest połączonych równolegle. Rozważmy trzy rezystory o różnych wartościach, jak pokazano na poniższym rysunku.

Indukcyjność
Całkowitą indukcyjność obwodu z równoległymi rezystorami oblicza się inaczej niż w przypadku metody szeregowej sieci indukcyjnej. Tutaj do odwrotności (1 / R) wartości poszczególnych indukcyjności dodaje się odwrotność sumy algebraicznej, aby uzyskać całkowitą wartość indukcyjności.
Całkowita wartość indukcyjności sieci wynosi
$$ \ frac {1} {L_ {T}} \: \: = \: \: \ frac {1} {L_ {1}} \: \: + \: \: \ frac {1} {L_ { 2}} \: \: + \: \: \ frac {1} {L_ {3}} $$
W którym L 1 jest indukcyjnością 1 st cewki indukcyjnej L 2 jest indukcyjnością 2 nd cewki i L 3 jest indukcyjnością 3 rd induktor w powyższym sieci.
Z metody obliczania indukcyjności równoległej możemy wyprowadzić proste równanie dla sieci równoległej z dwoma cewkami. To jest
$$ L_ {T} \: \: = \: \: \ frac {L_ {1} \: \: \ times \: \: L_ {2}} {L_ {1} \: \: + \: \ : L_ {2}} $$
Napięcie
Całkowite napięcie, które pojawia się w sieci równoległych cewek indukcyjnych jest takie samo, jak spadki napięcia na każdej indywidualnej indukcyjności.
Napięcie pojawiające się w obwodzie
$$ V \: \: = \: \: V_ {1} \: \: = \: \: V_ {2} \: \: = \: \: V_ {3} $$
Gdzie V 1 jest spadek napięcia na 1 st cewki V 2 jest spadek napięcia na 2 nd cewki i V 3 jest spadek napięcia na 3 -ciej induktor w powyższym sieci. Stąd napięcie jest takie samo we wszystkich punktach równoległej sieci cewek.
obecny
Całkowita ilość prądu wpływającego do równoległej sieci indukcyjnej jest sumą wszystkich pojedynczych prądów płynących we wszystkich równoległych gałęziach. Wartość indukcyjności każdej gałęzi określa wartość prądu, który przez nią przepływa.
Całkowity prąd w sieci wynosi
$$ I \: \: = \: \: I_ {1} \: \: + \: \: I_ {2} \: \: + \: \: I_ {3} $$
Gdzie I 1 jest prądem płynącym przez pierwszą cewkę indukcyjną, Ja 2 jest prądem płynącym przez drugą cewkę indukcyjną, a Ja 3 jest prądem płynącym przez trzecią cewkę w powyższej sieci.
Stąd suma poszczególnych prądów w różnych gałęziach daje całkowity prąd w sieci równoległej.
Reaktywność indukcyjna
Reaktancja indukcyjna to opozycja oferowana przez cewkę do przepływu prądu przemiennego lub po prostu prądu przemiennego. Cewka ma właściwość przeciwstawiania się zmianie przepływu prądu, a zatem wykazuje pewną opozycję, którą można określić jakoreactance, ponieważ częstotliwość prądu wejściowego należy również wziąć pod uwagę wraz z rezystancją, którą oferuje.
Wskazanie - XL
Jednostki - Ohms
Symbol - Ω
W obwodzie czysto indukcyjnym prąd IL lagsprzyłożone napięcie o 90 °. Reaktancja indukcyjna jest obliczana przez,
$$ X_ {L} \: \: = \: \: 2 \ pi fL $$
Gdzie f jest częstotliwością sygnału. Stąd reaktancja indukcyjna jest funkcją częstotliwości i indukcyjności.