Podstawowa elektronika - indukcyjność
Właściwość cewki indukcyjnej polegająca na uzyskaniu napięcia indukowanego przez zmianę przepływu prądu jest definiowana jako indukcyjność. Indukcyjność to stosunek napięcia do szybkości zmiany prądu.
Szybkość zmian prądu powoduje zmianę pola magnetycznego, które indukuje pole elektromagnetyczne w kierunku przeciwnym do źródła napięcia. Ta właściwość indukcji pola elektromagnetycznego jest nazywanaInductance.
Wzór na indukcyjność to
$$ Indukcyjność \: \: = \: \: \ frac {volatge} {stopa \: z \: zmiana \: z \: bieżąca} $$
Units −
Jednostką indukcyjności jest Henry. Wskazuje na toL.
Cewki są najczęściej dostępne w mH (milli Henry) i μH (mikro Henry).
Mówi się, że cewka ma indukcyjność one Henry kiedy EMF one volt jest samoindukowane w cewce, gdzie przepływający prąd zmieniał się z prędkością one ampere per second.
Indukcyjność własna
Jeśli rozważa się cewkę, w której płynie jakiś prąd, ma ona pewne pole magnetyczne, prostopadłe do przepływu prądu. Kiedy ten prąd ciągle się zmienia, pole magnetyczne również się zmienia, a to zmieniające się pole magnetyczne indukuje pole elektromagnetyczne przeciwne do napięcia źródła. Ten wytwarzany przeciwny EMF toself-induced voltage i ta metoda jest nazywana jako self-inductance.
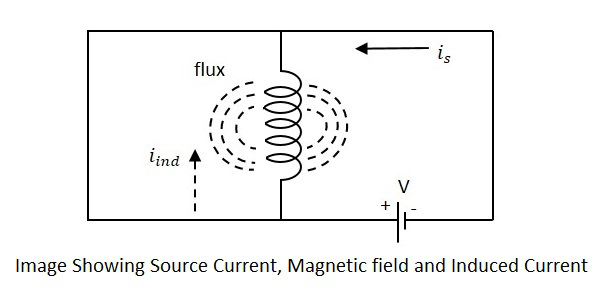
Obecny is na rysunku wskaż źródło prądu podczas iindwskazuje indukowany prąd. Strumień reprezentuje strumień magnetyczny wytworzony wokół cewki. Przy zastosowaniu napięcia prądispowstają przepływy i strumienie. Kiedy obecnyis zmienia się, strumień staje się zróżnicowany iind.
To indukowane pole elektromagnetyczne w cewce jest proporcjonalne do szybkości zmian prądu. Im wyższe tempo zmian prądu, tym wyższa wartość indukowanego pola elektromagnetycznego.
Powyższe równanie możemy zapisać jako
$$ E \: \: \ alpha \: \: \ frac {dI} {dt} $$
$$ E \: \: = \: \: L \: \: \ frac {dI} {dt} $$
Gdzie,
E jest wytwarzany EMF
dI/dt wskazuje szybkość zmian prądu
L wskazuje współczynnik indukcyjności.
Indukcyjność własna lub Współczynnik indukcyjności własnej można określić jako
$$ L \: \: = \: \: \ frac {E} {\ frac {dI} {dt}} $$
Rzeczywiste równanie jest zapisane jako
$$ E \: \: = \: \: - L \: \: \ frac {dI} {dt} $$
Wskazuje na to minus w powyższym równaniu the EMF is induced in opposite direction to the voltage source zgodnie z prawem Lenza.
Wzajemna indukcyjność
Ponieważ cewka przewodząca prąd wytwarza wokół siebie pewne pole magnetyczne, jeśli inna cewka zostanie zbliżona do tej cewki, tak że znajduje się w obszarze strumienia magnetycznego pierwotnego, wówczas zmieniający się strumień magnetyczny indukuje pole elektromagnetyczne w drugiej cewce. Jeśli ta pierwsza cewka jest nazywana jakoPrimary coil, drugi można nazwać jako Secondary coil.
Kiedy w cewce wtórnej indukowane jest pole elektromagnetyczne z powodu zmieniającego się pola magnetycznego cewki pierwotnej, to takie zjawisko nazywa się Mutual Inductance.
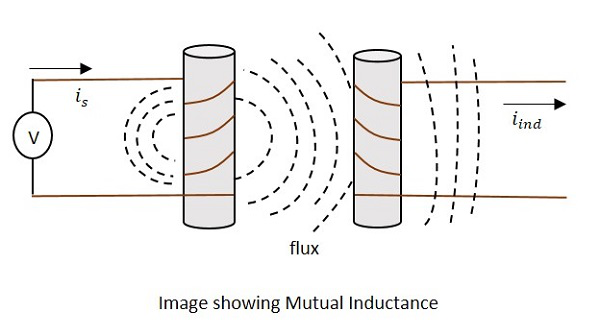
Obecny is na rysunku wskaż źródło prądu podczas iindwskazuje indukowany prąd. Strumień reprezentuje strumień magnetyczny wytworzony wokół cewki. To rozprzestrzenia się również na cewkę wtórną.
Przy zastosowaniu napięcia prąd ispowstają przepływy i strumienie. Kiedy obecnyis zmienia się, strumień staje się zróżnicowany iind w uzwojeniu wtórnym, ze względu na właściwość wzajemnej indukcyjności.
Zmiana nastąpiła w ten sposób.
$$ V_ {p} \: \: I_ {p} \ rightarrow \: \: B \: \: \ rightarrow \: \: V_ {s} \: \: I_ {s} $$
Gdzie,
Vp ip Wskaż odpowiednio napięcie i prąd w cewce pierwotnej
B Wskazuje strumień magnetyczny
Vs is Wskaż odpowiednio napięcie i prąd w cewce wtórnej
Wzajemna indukcyjność M z dwóch obwodów opisuje wielkość napięcia w obwodzie wtórnym indukowane przez zmiany prądu pierwotnego.
$$ V (Secondary) \: \: = \: \: - M \ frac {\ Delta I} {\ Delta t} $$
Gdzie $ \ frac {\ Delta I} {\ Delta t} $ tempo zmian prądu w czasie i Mjest współczynnikiem wzajemnej indukcyjności. Znak minus wskazuje kierunek przepływu prądu przeciwny do źródła.
Units −
Jednostki wzajemnej indukcyjności to
$$ volt \: \: = \: \: M \ frac {amps} {sec} $$
(Z powyższego równania)
$$ M \: \: = \: \: \ frac {volt. \: Sec} {amp} $$
$$ = \: \: Henry (H) $$
W zależności od liczby zwojów cewki pierwotnej i wtórnej zmienia się strumień magnetyczny i ilość indukowanego pola elektromagnetycznego. Liczba zwojów w podstawowym jest oznaczona przez N1, a wtórna przez N2. Współczynnik sprzężenia to termin określający wzajemną indukcyjność dwóch cewek.
Czynniki wpływające na indukcyjność
Istnieje kilka czynników, które wpływają na działanie cewki indukcyjnej. Najważniejsze z nich omówiono poniżej.
Długość cewki
Długość cewki induktora jest odwrotnie proporcjonalna do indukcyjności cewki. Jeśli długość cewki jest większa, indukcyjność oferowana przez tę cewkę zmniejsza się i odwrotnie.
Pole przekroju poprzecznego cewki
Pole przekroju poprzecznego cewki jest wprost proporcjonalne do indukcyjności cewki. Im większa powierzchnia cewki, tym wyższa będzie indukcyjność.
Liczba tur
Wraz z liczbą zwojów cewka wpływa bezpośrednio na indukcyjność. Wartość indukcyjności jest kwadratowa do liczby zwojów cewki. Stąd im większa liczba zwojów, tym jej kwadrat będzie wartością indukcyjności cewki.
Przepuszczalność rdzenia
Plik permeability (μ)materiału rdzenia induktora wskazuje podporę, którą rdzeń zapewnia tworzenie pola magnetycznego w sobie. Plikhigher przepuszczalność materiału rdzenia, higher będzie indukcyjność.
Współczynnik sprzężenia
Jest to ważny czynnik, który należy znać przy obliczaniu wzajemnej indukcyjności dwóch cewek. Rozważmy dwie pobliskie cewki zwojów N1 i N2.
Prąd płynący przez pierwszą cewkę i 1 wytwarza pewien strumień Ψ 1 . Ilość wiązań strumienia magnetycznego jest rozumiana przez zwoje Webera.
Niech ilość strumienia magnetycznego związanego z drugą cewką, ze względu na prąd jednostkowy i 1 będzie
$$ \ frac {N_ {2} \ varphi_ {1}} {i_ {1}} $$
Można to rozumieć jako Współczynnik Wzajemnej indukcyjności, co oznacza
$$ M \: \: = \: \: \ frac {N_ {2} \ varphi_ {1}} {i_ {1}} $$
Stąd współczynnik wzajemnej indukcyjności między dwiema cewkami lub obwodami jest rozumiany jako zwoje Webera w jednej cewce na skutek 1A prądu w drugiej cewce.
Jeśli indukcyjność własna pierwszej cewki wynosi L 1 , to
$$ L_ {1} i_ {1} \: \: = \: \: {N_ {1} \ varphi_ {1}} \: \: => \: \: \ frac {L_ {1}} {N_ {1}} \: \: \ frac {\ varphi_ {1}} {i_ {1}} $$
$$ M \: \: = \: \: \ frac {N_ {2} L_ {1}} {N_ {1}} $$
Podobnie, współczynnik wzajemnej indukcyjności od prądu i 2 w drugiej cewce wynosi
$$ M \: \: = \: \: \ frac {N_ {1} \ varphi_ {2}} {i_ {2}} \: \ dotsm \: \ dotsm \: \ dotsm \: \ dotsm \: \ : 1 $$
Jeżeli indukcyjność własna drugiej cewki wynosi L 2
$$ L_ {2} i_ {2} \: \: = \: \: N_ {2} \ varphi_ {2} $$
$$ \ frac {L_ {2}} {N_ {2}} \: \: = \: \: \ frac {\ varphi_ {2}} {i_ {2}} $$
W związku z tym,
$$ M \: \: = \: \: \ frac {N_ {1} L_ {2}} {N_ {2}} \: \ dotsm \: \ dotsm \: \ dotsm \: \ dotsm \: \: 2 $$
Mnożąc 1 i 2, otrzymujemy
$$ M \: \: \ times \: \: M = \: \: \ frac {N_ {2} L_ {1}} {N_ {1}} \: \: \ times \: \: \ frac { N_ {1} L_ {2}} {N_ {2}} $$
$$ M ^ {2} \: \: = \: \: L_ {1} L_ {2} \: \: => \: \: M \: \: = \: \: \ sqrt {L_ {1 } L_ {2}} $$
Powyższe równanie jest prawdziwe, gdy cały zmieniający się strumień cewki pierwotnej łączy się z cewką wtórną, co jest przypadkiem idealnym. Ale w praktyce tak nie jest. Dlatego możemy pisać jako
$$ M \: \: \ neq \: \: \ sqrt {L_ {1} L_ {2}} $$
$$ i \ frac {M} {\ sqrt {L_ {1} L_ {2}}} \: \: = \: \: K \: \: \ neq \: \: 1 $$
Gdzie K jest znane jako współczynnik sprzężenia.
Plik Coefficient of coupling K można zdefiniować jako stosunek rzeczywistego współczynnika wzajemnej indukcyjności do idealnego (maksymalnego) współczynnika wzajemnej indukcyjności.
Jeśli wartość k jest bliska jedności, to mówi się, że cewki są ściśle połączone, a jeśli wartość k = 0, to cewki są luźno połączone.
Zastosowania cewek
Istnieje wiele zastosowań cewek, takich jak -
Cewki indukcyjne są używane w obwodach filtrów do wykrywania składowych o wysokiej częstotliwości i tłumienia sygnałów szumu
Aby odizolować obwód od niepożądanych sygnałów HF.
Cewki indukcyjne są używane w obwodach elektrycznych do tworzenia transformatora i izolowania obwodów od kolców.
Cewki indukcyjne są również stosowane w silnikach.