Big Data Analytics - metody statystyczne
Analizując dane, można przyjąć podejście statystyczne. Podstawowe narzędzia potrzebne do wykonania podstawowej analizy to -
- Analiza korelacji
- Analiza wariancji
- Testowanie hipotez
Podczas pracy z dużymi zbiorami danych nie stanowi to problemu, ponieważ te metody nie wymagają intensywnych obliczeń, z wyjątkiem analizy korelacji. W takim przypadku zawsze można pobrać próbkę, a wyniki powinny być rzetelne.
Analiza korelacji
Analiza korelacji ma na celu znalezienie liniowych zależności między zmiennymi numerycznymi. Może to być przydatne w różnych okolicznościach. Jednym z powszechnych zastosowań jest eksploracyjna analiza danych, w sekcji 16.0.2 książki znajduje się podstawowy przykład tego podejścia. Po pierwsze, metryka korelacji użyta w tym przykładzie jest oparta naPearson coefficient. Istnieje jednak inna interesująca miara korelacji, na którą wartości odstające nie mają wpływu. Ta miara nazywa się korelacją włócznika.
Plik spearman correlation metryka jest bardziej odporna na obecność wartości odstających niż metoda Pearsona i daje lepsze oszacowania zależności liniowych między zmiennymi liczbowymi, gdy dane nie mają rozkładu normalnego.
library(ggplot2)
# Select variables that are interesting to compare pearson and spearman
correlation methods.
x = diamonds[, c('x', 'y', 'z', 'price')]
# From the histograms we can expect differences in the correlations of both
metrics.
# In this case as the variables are clearly not normally distributed, the
spearman correlation
# is a better estimate of the linear relation among numeric variables.
par(mfrow = c(2,2))
colnm = names(x)
for(i in 1:4) {
hist(x[[i]], col = 'deepskyblue3', main = sprintf('Histogram of %s', colnm[i]))
}
par(mfrow = c(1,1))Z histogramów na poniższym rysunku możemy spodziewać się różnic w korelacjach obu wskaźników. W tym przypadku, ponieważ zmienne wyraźnie nie mają rozkładu normalnego, korelacja Spearmana jest lepszym oszacowaniem liniowej zależności między zmiennymi numerycznymi.
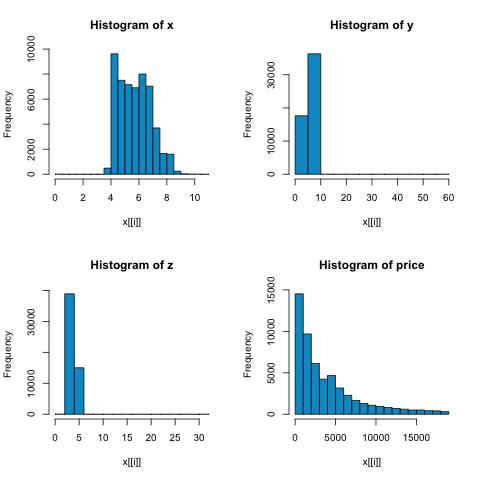
Aby obliczyć korelację w R, otwórz plik bda/part2/statistical_methods/correlation/correlation.R który ma tę sekcję kodu.
## Correlation Matrix - Pearson and spearman
cor_pearson <- cor(x, method = 'pearson')
cor_spearman <- cor(x, method = 'spearman')
### Pearson Correlation
print(cor_pearson)
# x y z price
# x 1.0000000 0.9747015 0.9707718 0.8844352
# y 0.9747015 1.0000000 0.9520057 0.8654209
# z 0.9707718 0.9520057 1.0000000 0.8612494
# price 0.8844352 0.8654209 0.8612494 1.0000000
### Spearman Correlation
print(cor_spearman)
# x y z price
# x 1.0000000 0.9978949 0.9873553 0.9631961
# y 0.9978949 1.0000000 0.9870675 0.9627188
# z 0.9873553 0.9870675 1.0000000 0.9572323
# price 0.9631961 0.9627188 0.9572323 1.0000000Test chi-kwadrat
Test chi kwadrat pozwala nam sprawdzić, czy dwie zmienne losowe są niezależne. Oznacza to, że rozkład prawdopodobieństwa każdej zmiennej nie wpływa na drugą. Aby ocenić test w R, musimy najpierw utworzyć tabelę kontyngencji, a następnie przekazać ją dochisq.test R funkcjonować.
Na przykład, sprawdźmy, czy istnieje powiązanie między zmiennymi: szlifem i kolorem ze zbioru danych o diamentach. Test jest formalnie zdefiniowany jako -
- H0: Zmienne cięcie i diament są niezależne
- H1: Zmienna szlif i diament nie są niezależne
Zakładalibyśmy, że istnieje związek między tymi dwiema zmiennymi poprzez ich nazwy, ale test może dać obiektywną „regułę” mówiącą, jak istotny jest ten wynik, czy nie.
W poniższym fragmencie kodu stwierdziliśmy, że wartość p testu wynosi 2,2e-16, co w praktyce jest prawie zerowe. Następnie po uruchomieniu testu wykonując plikMonte Carlo simulation, stwierdziliśmy, że wartość p wynosi 0,0004998, co jest nadal dość niższe niż próg 0,05. Ten wynik oznacza, że odrzucamy hipotezę zerową (H0), więc wierzymy zmiennymcut i color nie są niezależni.
library(ggplot2)
# Use the table function to compute the contingency table
tbl = table(diamonds$cut, diamonds$color)
tbl
# D E F G H I J
# Fair 163 224 312 314 303 175 119
# Good 662 933 909 871 702 522 307
# Very Good 1513 2400 2164 2299 1824 1204 678
# Premium 1603 2337 2331 2924 2360 1428 808
# Ideal 2834 3903 3826 4884 3115 2093 896
# In order to run the test we just use the chisq.test function.
chisq.test(tbl)
# Pearson’s Chi-squared test
# data: tbl
# X-squared = 310.32, df = 24, p-value < 2.2e-16
# It is also possible to compute the p-values using a monte-carlo simulation
# It's needed to add the simulate.p.value = TRUE flag and the amount of
simulations
chisq.test(tbl, simulate.p.value = TRUE, B = 2000)
# Pearson’s Chi-squared test with simulated p-value (based on 2000 replicates)
# data: tbl
# X-squared = 310.32, df = NA, p-value = 0.0004998Test T.
Pomysł t-testpolega na ocenie, czy istnieją różnice w liczbowym rozkładzie zmiennych # między różnymi grupami zmiennej nominalnej. Aby to zademonstrować, wybiorę poziomy Dostatecznego i Idealnego cięcia zmiennej czynnikowej, a następnie porównamy wartości zmiennej numerycznej między tymi dwiema grupami.
data = diamonds[diamonds$cut %in% c('Fair', 'Ideal'), ]
data$cut = droplevels.factor(data$cut) # Drop levels that aren’t used from the
cut variable
df1 = data[, c('cut', 'price')]
# We can see the price means are different for each group
tapply(df1$price, df1$cut, mean)
# Fair Ideal
# 4358.758 3457.542Testy t są implementowane w języku R z rozszerzeniem t.testfunkcjonować. Interfejs formuły do t.test jest najprostszym sposobem jego użycia, chodzi o to, że zmienna numeryczna jest wyjaśniona przez zmienną grupową.
Na przykład: t.test(numeric_variable ~ group_variable, data = data). W poprzednim przykładzienumeric_variable jest price i group_variable jest cut.
Z perspektywy statystycznej sprawdzamy, czy istnieją różnice w rozkładach zmiennej liczbowej między dwiema grupami. Formalnie test hipotezy jest opisany hipotezą zerową (H0) i hipotezą alternatywną (H1).
H0: Nie ma różnic w rozkładach zmiennej ceny między grupami Fair i Ideal
H1 Występują różnice w rozkładach zmiennej ceny między grupami Fair i Ideal
Poniższe można zaimplementować w języku R za pomocą następującego kodu -
t.test(price ~ cut, data = data)
# Welch Two Sample t-test
#
# data: price by cut
# t = 9.7484, df = 1894.8, p-value < 2.2e-16
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# 719.9065 1082.5251
# sample estimates:
# mean in group Fair mean in group Ideal
# 4358.758 3457.542
# Another way to validate the previous results is to just plot the
distributions using a box-plot
plot(price ~ cut, data = data, ylim = c(0,12000),
col = 'deepskyblue3')Możemy przeanalizować wynik testu, sprawdzając, czy wartość p jest niższa niż 0,05. W takim przypadku zachowujemy hipotezę alternatywną. Oznacza to, że znaleźliśmy różnice cen między dwoma poziomami współczynnika obniżki. Po nazwach poziomów spodziewalibyśmy się takiego wyniku, ale nie spodziewalibyśmy się, że średnia cena w grupie Fail będzie wyższa niż w grupie Ideal. Możemy to zobaczyć, porównując średnie każdego czynnika.
Plik plotpolecenie tworzy wykres pokazujący zależność między ceną a zmienną cięcia. To jest wykres pudełkowy; wykres ten omówiliśmy w sekcji 16.0.1, ale zasadniczo pokazuje on rozkład zmiennej ceny dla dwóch analizowanych przez nas poziomów cięcia.
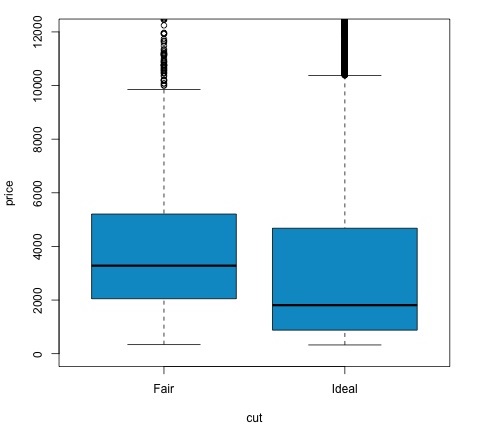
Analiza wariancji
Analiza wariancji (ANOVA) to model statystyczny używany do analizy różnic między rozkładami grup poprzez porównanie średniej i wariancji w każdej grupie, model został opracowany przez Ronalda Fishera. ANOVA zapewnia statystyczny test tego, czy średnie z kilku grup są równe, a zatem uogólnia test t na więcej niż dwie grupy.
ANOVA są przydatne do porównywania trzech lub więcej grup pod kątem istotności statystycznej, ponieważ wykonanie wielu testów t dla dwóch prób skutkowałoby zwiększeniem szansy popełnienia błędu statystycznego typu I.
Jeśli chodzi o wyjaśnienie matematyczne, do zrozumienia testu potrzebne są następujące informacje.
x ij = x + (x i - x) + (x ij - x)
Prowadzi to do następującego modelu -
x ij = μ + α i + ∈ ij
gdzie μ jest średnią wielką, a α i jest średnią i -tej grupy. Zakłada się, że składnik błędu ∈ ij jest iid z rozkładu normalnego. Hipoteza zerowa testu jest taka, że -
α 1 = α 2 =… = α k
Jeśli chodzi o obliczanie statystyki testowej, musimy obliczyć dwie wartości -
- Suma kwadratów różnicy między grupami -
$$ SSD_B = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x _ {\ bar {i}}} - \ bar {x}) ^ 2 $$
- Sumy kwadratów w grupach
$$ SSD_W = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x _ {\ bar {ij}}} - \ bar {x _ {\ bar {i}}}) ^ 2 $$
gdzie SSD B ma stopień swobody k-1, a SSD W ma stopień swobody N-k. Następnie możemy zdefiniować średnie kwadratowe różnice dla każdej metryki.
MS B = SSD B / (k - 1)
MS w = SSD z / (N - k)
Wreszcie statystyka testowa w ANOVA jest definiowana jako stosunek powyższych dwóch wielkości
F = MS B / MS w
który następuje po rozkładzie F z k-1 i N-k stopniami swobody. Jeśli hipoteza zerowa jest prawdziwa, F prawdopodobnie będzie bliskie 1. W przeciwnym razie średni kwadratowy MSB między grupami będzie prawdopodobnie duży, co skutkuje dużą wartością F.
Zasadniczo ANOVA bada dwa źródła całkowitej wariancji i widzi, która część ma większy wpływ. Dlatego nazywa się to analizą wariancji, chociaż celem jest porównanie średnich grupowych.
Jeśli chodzi o obliczanie statystyki, jest to raczej proste do zrobienia w R. Poniższy przykład pokaże, jak to się robi i wykreśli wyniki.
library(ggplot2)
# We will be using the mtcars dataset
head(mtcars)
# mpg cyl disp hp drat wt qsec vs am gear carb
# Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
# Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
# Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
# Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
# Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
# Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
# Let's see if there are differences between the groups of cyl in the mpg variable.
data = mtcars[, c('mpg', 'cyl')]
fit = lm(mpg ~ cyl, data = mtcars)
anova(fit)
# Analysis of Variance Table
# Response: mpg
# Df Sum Sq Mean Sq F value Pr(>F)
# cyl 1 817.71 817.71 79.561 6.113e-10 ***
# Residuals 30 308.33 10.28
# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 .
# Plot the distribution
plot(mpg ~ as.factor(cyl), data = mtcars, col = 'deepskyblue3')Kod wygeneruje następujący wynik -

Wartość p, którą otrzymujemy w przykładzie, jest znacznie mniejsza niż 0,05, więc R zwraca symbol „***”, aby to oznaczyć. Oznacza to, że odrzucamy hipotezę zerową i znajdujemy różnice między średnimi mpg między różnymi grupamicyl zmienna.