Big Data Analytics - Analiza szeregów czasowych
Szeregi czasowe to sekwencja obserwacji zmiennych kategorialnych lub numerycznych indeksowanych według daty lub sygnatury czasowej. Wyraźnym przykładem danych szeregów czasowych są szeregi czasowe ceny akcji. W poniższej tabeli możemy zobaczyć podstawową strukturę danych szeregów czasowych. W tym przypadku obserwacje są rejestrowane co godzinę.
| Znak czasu | Cena akcji |
|---|---|
| 11.10.2015 09:00:00 | 100 |
| 11.10.2015 10:00:00 | 110 |
| 11.10.2015 11:00:00 | 105 |
| 11.10.2015 12:00:00 | 90 |
| 11.10.2015 13:00:00 | 120 |
Zwykle pierwszym krokiem w analizie szeregów czasowych jest wykreślenie szeregu, zwykle odbywa się to za pomocą wykresu liniowego.
Najpowszechniejszym zastosowaniem analizy szeregów czasowych jest prognozowanie przyszłych wartości wartości liczbowej przy użyciu struktury czasowej danych. Oznacza to, że dostępne obserwacje służą do przewidywania wartości z przyszłości.
Uporządkowanie danych w czasie oznacza, że tradycyjne metody regresji nie są przydatne. Aby zbudować solidną prognozę, potrzebujemy modeli uwzględniających czasowe uporządkowanie danych.
Najpopularniejszy model analizy szeregów czasowych nosi nazwę Autoregressive Moving Average(ARMA). Model składa się z dwóch części, anautoregressive (AR) część i a moving average(MA) cz. Model jest zwykle nazywany modelem ARMA (p, q), gdzie p jest rzędem części autoregresyjnej, a q jest rzędem części średniej ruchomej.
Model autoregresyjny
AR (p) jest odczytywana jako Model AR rzędu p. Matematycznie jest napisane jako -
$$ X_t = c + \ sum_ {i = 1} ^ {P} \ phi_i X_ {t - i} + \ varepsilon_ {t} $$
gdzie {φ 1 ,…, φ p } to parametry do oszacowania, c jest stałą, a zmienna losowa ε t reprezentuje biały szum. Konieczne są pewne ograniczenia wartości parametrów, aby model pozostał nieruchomy.
Średnia krocząca
Notacja MA (q) odnosi się do modelu średniej ruchomej rzędu q -
$$ X_t = \ mu + \ varepsilon_t + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {t - i} $$
gdzie θ 1 , ..., θ q są parametrami modelu, μ jest oczekiwaniem X t , a ε t , ε t - 1 , ... są składnikami błędu białego szumu.
Autoregresywna średnia krocząca
Model ARMA (p, q) łączy warunki p autoregresyjne i q średniej ruchomej. Matematycznie model jest wyrażony następującym wzorem -
$$ X_t = c + \ varepsilon_t + \ sum_ {i = 1} ^ {P} \ phi_iX_ {t - 1} + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {ti} $$
Widzimy, że model ARMA (p, q) jest połączeniem modeli AR (p) i MA (q) .
Aby dać pewną intuicję modelu, weźmy pod uwagę, że część AR równania dąży do oszacowania parametrów dla obserwacji X t - i w celu przewidzenia wartości zmiennej w X t . Ostatecznie jest to średnia ważona poprzednich wartości. Sekcja MA stosuje to samo podejście, ale z błędem poprzednich obserwacji ε t - i . Ostatecznie wynikiem modelu jest średnia ważona.
Poniższy kod ilustruje sposób wdrożenia ARMA (p, q) w R .
# install.packages("forecast")
library("forecast")
# Read the data
data = scan('fancy.dat')
ts_data <- ts(data, frequency = 12, start = c(1987,1))
ts_data
plot.ts(ts_data)Wykreślenie danych jest zwykle pierwszym krokiem do ustalenia, czy dane mają strukturę czasową. Z wykresu widać, że pod koniec każdego roku są silne skoki.
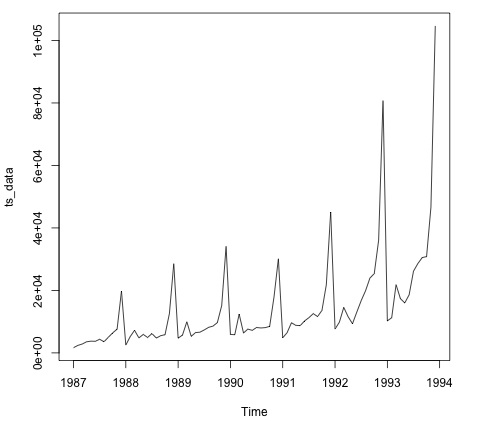
Poniższy kod dopasowuje model ARMA do danych. Uruchamia kilka kombinacji modeli i wybiera ten, który ma mniej błędów.
# Fit the ARMA model
fit = auto.arima(ts_data)
summary(fit)
# Series: ts_data
# ARIMA(1,1,1)(0,1,1)[12]
# Coefficients:
# ar1 ma1 sma1
# 0.2401 -0.9013 0.7499
# s.e. 0.1427 0.0709 0.1790
#
# sigma^2 estimated as 15464184: log likelihood = -693.69
# AIC = 1395.38 AICc = 1395.98 BIC = 1404.43
# Training set error measures:
# ME RMSE MAE MPE MAPE MASE ACF1
# Training set 328.301 3615.374 2171.002 -2.481166 15.97302 0.4905797 -0.02521172