Projekt kompilatora - automaty skończone
Automaty skończone to maszyna stanów, która pobiera ciąg symboli jako dane wejściowe i odpowiednio zmienia swój stan. Automaty skończone to aparat rozpoznawania wyrażeń regularnych. Kiedy ciąg wyrażenia regularnego jest wprowadzany do automatów skończonych, zmienia swój stan dla każdego literału. Jeśli ciąg wejściowy został pomyślnie przetworzony i automaty osiągną swój stan końcowy, jest on akceptowany, tj. O podanym właśnie łańcuchu mówi się, że jest prawidłowym tokenem używanego języka.
Model matematyczny automatów skończonych składa się z:
- Skończony zbiór stanów (Q)
- Skończony zbiór symboli wejściowych (Σ)
- Jeden stan początkowy (q0)
- Zbiór stanów końcowych (qf)
- Funkcja przejścia (δ)
Funkcja przejścia (δ) odwzorowuje skończony zbiór stanu (Q) na skończony zbiór symboli wejściowych (Σ), Q × Σ ➔ Q
Konstrukcja automatów skończonych
Niech L (r) będzie językiem regularnym rozpoznawanym przez jakieś automaty skończone (FA).
States: Stany FA są reprezentowane przez kółka. Nazwy stanów są zapisane w kółkach.
Start state: Stan, w którym automaty się uruchamiają, nazywany jest stanem początkowym. Stan początkowy ma skierowaną w jego stronę strzałkę.
Intermediate states: Wszystkie stany pośrednie mają co najmniej dwie strzałki; jeden wskazuje, a drugi wskazuje od nich.
Final state: Jeśli wejściowy ciąg znaków został pomyślnie przeanalizowany, oczekuje się, że automaty będą w tym stanie. Stan końcowy jest reprezentowany przez podwójne okręgi. Może mieć dowolną nieparzystą liczbę strzałek wskazujących na niego i parzystą liczbę strzałek wskazujących z niego. Liczba strzał nieparzystych jest o jeden większa niż parzysta, tjodd = even+1.
Transition: Przejście z jednego stanu do innego stanu następuje, gdy na wejściu zostanie znaleziony żądany symbol. Po przejściu automaty mogą albo przejść do następnego stanu, albo pozostać w tym samym stanie. Przejście z jednego stanu do drugiego jest pokazane jako skierowana strzałka, w której strzałki wskazują stan docelowy. Jeśli automaty pozostają w tym samym stanie, rysowana jest strzałka wskazująca ze stanu do samego siebie.
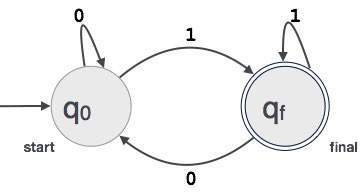
Example: Zakładamy, że FA akceptuje dowolną trzycyfrową wartość binarną kończącą się cyfrą 1. FA = {Q (q 0 , q f ), Σ (0,1), q 0 , q f , δ}