Uczenie maszynowe - umiejętności
Uczenie maszynowe ma bardzo dużą szerokość i wymaga umiejętności w kilku dziedzinach. Umiejętności, które musisz zdobyć, aby zostać ekspertem w dziedzinie uczenia maszynowego, są wymienione poniżej -
- Statistics
- Teorie prawdopodobieństwa
- Calculus
- Techniki optymalizacji
- Visualization
Konieczność różnych umiejętności uczenia maszynowego
Aby dać ci krótkie wyobrażenie o umiejętnościach, które musisz zdobyć, omówimy kilka przykładów -
Notacja matematyczna
Większość algorytmów uczenia maszynowego opiera się w dużej mierze na matematyce. Poziom matematyki, który musisz znać, to prawdopodobnie poziom początkujący. Ważne jest, abyś był w stanie przeczytać notację, której matematycy używają w swoich równaniach. Na przykład - jeśli jesteś w stanie przeczytać notację i zrozumieć, co to znaczy, jesteś gotowy do nauki uczenia maszynowego. Jeśli nie, być może będziesz musiał odświeżyć swoją wiedzę matematyczną.
$$ f_ {AN} (net- \ theta) = \ begin {cases} \ gamma & if \: net- \ theta \ geq \ epsilon \\ net- \ theta & if - \ epsilon <net- \ theta <\ epsilon \\ - \ gamma & if \: net- \ theta \ leq- \ epsilon \ end {sprawy} $$
$$ \ Displaystyle \\\ max \ limity _ {\ alfa} \ rozpocząć {bmatrix} \ Displaystyle \ sum \ limity_ {i = 1} ^ m \ alpha- \ Frac {1} {2} \ Displaystyle \ sum \ limity_ { i, j = 1} ^ m label ^ \ left (\ begin {array} {c} i \\ \ end {array} \ right) \ cdot \: label ^ \ left (\ begin {tablica} {c} j \\ \ end {array} \ right) \ cdot \: a_ {i} \ cdot \: a_ {j} \ langle x ^ \ left (\ begin {array} {c} i \\ \ end {array} \ po prawej), x ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ rangle \ end {bmatrix} $$
$$ f_ {AN} (net- \ theta) = \ left (\ frac {e ^ {\ lambda (net- \ theta)} - e ^ {- \ lambda (net- \ theta)}} {e ^ { \ lambda (net- \ theta)} + e ^ {- \ lambda (net- \ theta)}} \ right) \; $$
Teoria prawdopodobieństwa
Oto przykład, aby sprawdzić swoją obecną wiedzę na temat teorii prawdopodobieństwa: Klasyfikacja za pomocą prawdopodobieństw warunkowych.
$$ p (c_ {i} | x, y) \; = \ frac {p (x, y | c_ {i}) \; p (c_ {i}) \;} {p (x, y) \ ;} $$
Dzięki tym definicjom możemy zdefiniować regułę klasyfikacji Bayesa -
- Jeśli P (c1 | x, y)> P (c2 | x, y), klasa to c1.
- Jeśli P (c1 | x, y) <P (c2 | x, y), klasa to c2.
Problem optymalizacji
Oto funkcja optymalizacji
$$ \ Displaystyle \\\ max \ limity _ {\ alfa} \ rozpocząć {bmatrix} \ Displaystyle \ sum \ limity_ {i = 1} ^ m \ alpha- \ Frac {1} {2} \ Displaystyle \ sum \ limity_ { i, j = 1} ^ m label ^ \ left (\ begin {array} {c} i \\ \ end {array} \ right) \ cdot \: label ^ \ left (\ begin {tablica} {c} j \\ \ end {array} \ right) \ cdot \: a_ {i} \ cdot \: a_ {j} \ langle x ^ \ left (\ begin {array} {c} i \\ \ end {array} \ po prawej), x ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ rangle \ end {bmatrix} $$
Z zastrzeżeniem następujących ograniczeń -
$$ \ alpha \ geq0 i \: \ displaystyle \ sum \ limit_ {i-1} ^ m \ alpha_ {i} \ cdot \: etykieta ^ \ lewo (\ początek {tablica} {c} ja \\ \ koniec {tablica} \ right) = 0 $$
Jeśli potrafisz przeczytać i zrozumieć powyższe, wszystko jest gotowe.
Wyobrażanie sobie
W wielu przypadkach będziesz musiał zrozumieć różne typy wykresów wizualizacyjnych, aby zrozumieć dystrybucję danych i zinterpretować wyniki algorytmu.
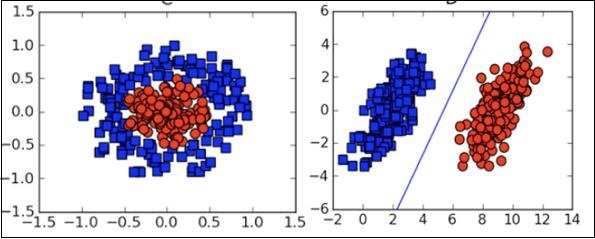
Oprócz powyższych teoretycznych aspektów uczenia maszynowego, do kodowania tych algorytmów potrzebne są dobre umiejętności programistyczne.
Więc co trzeba zrobić, aby wdrożyć ML? Przyjrzyjmy się temu w następnym rozdziale.