MATLAB - różnicowy

MATLAB zapewnia diffpolecenie do obliczania symbolicznych pochodnych. W najprostszej formie jako argument przekazujesz funkcję, którą chcesz odróżnić, do polecenia diff.

Na przykład obliczmy pochodną funkcji f (t) = 3t ² + 2t ^-2

Przykład

Utwórz plik skryptu i wpisz w nim następujący kod -

syms t
f = 3*t^2 + 2*t^(-2);
diff(f)

Kiedy powyższy kod jest kompilowany i wykonywany, daje następujący wynik -

ans =
6*t - 4/t^3

Poniżej znajduje się odpowiednik oktawowy powyższego obliczenia -

pkg load symbolic
symbols

t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)

Octave wykonuje kod i zwraca następujący wynik -

ans =
   -(4.0)*t^(-3.0)+(6.0)*t

Weryfikacja elementarnych reguł różnicowania

Przedstawmy pokrótce różne równania lub reguły różniczkowania funkcji i zweryfikujmy te zasady. W tym celu zapiszemy f '(x) dla pochodnej pierwszego rzędu, a f "(x) dla pochodnej drugiego rzędu.

Oto zasady różnicowania -

Zasada nr 1

Dla dowolnych funkcji f i g oraz dowolnych liczb rzeczywistych a i b są pochodną funkcji -

h(x) = af(x) + bg(x) w odniesieniu do x jest dane przez -

h'(x) = af'(x) + bg'(x)

Zasada 2

Plik sum i subtraction reguły mówią, że jeśli f i g są dwiema funkcjami, to odpowiednio f 'i g' są ich pochodnymi, to

(f + g)' = f' + g'

(f - g)' = f' - g'

Zasada 3

Plik product reguła mówi, że jeśli f i g są dwiema funkcjami, to odpowiednio f 'i g' są ich pochodnymi, to

(f.g)' = f'.g + g'.f

Zasada 4

Plik quotient reguła mówi, że jeśli f i g są dwiema funkcjami, to odpowiednio f 'i g' są ich pochodnymi, to

(f/g)' = (f'.g - g'.f)/g²

Zasada 5

Plik polynomial lub elementarna reguła władzy mówi, że jeśli y = f(x) = xⁿ, następnie f' = n. x^(n-1)

Bezpośrednim skutkiem tej reguły jest to, że pochodna dowolnej stałej wynosi zero, tj. Jeśli y = k, więc jakakolwiek stała

f' = 0

Zasada 6

Plik chain reguła stwierdza, że pochodna funkcji funkcji h(x) = f(g(x)) w odniesieniu do x jest,

h'(x)= f'(g(x)).g'(x)

Przykład

Utwórz plik skryptu i wpisz w nim następujący kod -

syms x
syms t

f = (x + 2)*(x^2 + 3)
der1 = diff(f)

f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)

f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)

f = (x^2 + 1)^17
der5 = diff(f)

f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)

Po uruchomieniu pliku MATLAB wyświetla następujący wynik -

f =
   (x^2 + 3)*(x + 2)
 
   der1 =
   2*x*(x + 2) + x^2 + 3
  
f =
   (t^(1/2) + t^3)*(t^2 + 3)
 
   der2 =
   (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
  
f =
   (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
  
der3 =
   (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
 
f =
   (2*x^2 + 3*x)/(x^3 + 1)
  
der4 =
   (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
  
f =
   (x^2 + 1)^17
  
der5 =
   34*x*(x^2 + 1)^16
  
f =
   1/(t^3 + 3*t^2 + 5*t - 9)^6
  
der6 =
   -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7

Poniżej znajduje się odpowiednik oktawowy powyższego obliczenia -

pkg load symbolic
symbols

x = sym("x");
t = sym("t");

f = (x + 2)*(x^2 + 3) 
der1 = differentiate(f,x) 

f = (t^2 + 3)*(t^(1/2) + t^3) 
der2 = differentiate(f,t) 

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) 
der3 = differentiate(f,x) 

f = (2*x^2 + 3*x)/(x^3 + 1) 
der4 = differentiate(f,x) 

f = (x^2 + 1)^17 
der5 = differentiate(f,x) 

f = (t^3 + 3* t^2 + 5*t -9)^(-6) 
der6 = differentiate(f,t)

Octave wykonuje kod i zwraca następujący wynik -

f =

(2.0+x)*(3.0+x^(2.0))
der1 =

3.0+x^(2.0)+(2.0)*(2.0+x)*x
f =

(t^(3.0)+sqrt(t))*(3.0+t^(2.0))
der2 =

(2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0))
f =

(1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))
der3 =

(-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x)
f =

(1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x)
der4 =

(1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x)
f =

(1.0+x^(2.0))^(17.0)
der5 =

(34.0)*(1.0+x^(2.0))^(16.0)*x
f =

(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0)
der6 =

-(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)

Pochodne funkcji wykładniczej, logarytmicznej i trygonometrycznej

Poniższa tabela zawiera pochodne powszechnie używanych funkcji wykładniczych, logarytmicznych i trygonometrycznych -

Funkcjonować	Pochodna
c^a.x	c ^a.x .ln ca (ln to logarytm naturalny)
e^x	e ^x
ln x	1 / x
ln_cx	1 / x.ln c
x^x	x ^x . (1 + ln x)
sin(x)	cos (x)
cos(x)	-sin (x)
tan(x)	sec ² (x) lub 1 / cos ² (x) lub 1 + tan ² (x)
cot(x)	-csc ² (x) lub -1 / sin ² (x) lub - (1 + cot ² (x))
sec(x)	sec (x). tan (x)
csc(x)	-csc (x) .cot (x)

Przykład

Utwórz plik skryptu i wpisz w nim następujący kod -

syms x
y = exp(x)
diff(y)

y = x^9
diff(y)

y = sin(x)
diff(y)

y = tan(x)
diff(y)

y = cos(x)
diff(y)

y = log(x)
diff(y)

y = log10(x)
diff(y)

y = sin(x)^2
diff(y)

y = cos(3*x^2 + 2*x + 1)
diff(y)

y = exp(x)/sin(x)
diff(y)

Po uruchomieniu pliku MATLAB wyświetla następujący wynik -

y =
   exp(x)
   ans =
   exp(x)

y =
   x^9
   ans =
   9*x^8
  
y =
   sin(x)
   ans =
   cos(x)
  
y =
   tan(x)
   ans =
   tan(x)^2 + 1
 
y =
   cos(x)
   ans =
   -sin(x)
  
y =
   log(x)
   ans =
   1/x
  
y =
   log(x)/log(10)
   ans =
   1/(x*log(10))
 
y =
   sin(x)^2
   ans =
   2*cos(x)*sin(x)
 
y =
   cos(3*x^2 + 2*x + 1)
   ans =
   -sin(3*x^2 + 2*x + 1)*(6*x + 2)
  
y =
   exp(x)/sin(x)
   ans =
   exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2

Poniżej znajduje się odpowiednik oktawowy powyższego obliczenia -

pkg load symbolic
symbols

x = sym("x");
y = Exp(x)
differentiate(y,x)

y = x^9
differentiate(y,x)

y = Sin(x)
differentiate(y,x)

y = Tan(x)
differentiate(y,x)

y = Cos(x)
differentiate(y,x)

y = Log(x)
differentiate(y,x)

% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)

y = Sin(x)^2
differentiate(y,x)

y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)

y = Exp(x)/Sin(x)
differentiate(y,x)

Octave wykonuje kod i zwraca następujący wynik -

y =

exp(x)
ans =

exp(x)
y =

x^(9.0)
ans =

(9.0)*x^(8.0)
y =

sin(x)
ans =

cos(x)
y =

tan(x)
ans =

1+tan(x)^2
y =

cos(x)
ans =

-sin(x)
y =

log(x)
ans =

x^(-1)
y =

sin(x)^(2.0)
ans =

(2.0)*sin(x)*cos(x)
y =

cos(1.0+(2.0)*x+(3.0)*x^(2.0))
ans =

-(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0))
y =

sin(x)^(-1)*exp(x)
ans =

sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)

Obliczanie pochodnych wyższego rzędu

Aby obliczyć wyższe pochodne funkcji f, używamy składni diff(f,n).

Obliczmy drugą pochodną funkcji y = f (x) = x. ^{E -3x}

f = x*exp(-3*x);
diff(f, 2)

MATLAB wykonuje kod i zwraca następujący wynik -

ans =
9*x*exp(-3*x) - 6*exp(-3*x)

Poniżej znajduje się odpowiednik oktawowy powyższego obliczenia -

pkg load symbolic
symbols

x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)

Octave wykonuje kod i zwraca następujący wynik -

ans =

(9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)

Przykład

W tym przykładzie rozwiążmy problem. Biorąc pod uwagę, że funkcjay = f(x) = 3 sin(x) + 7 cos(5x). Będziemy musieli dowiedzieć się, czy równanief" + f = -5cos(2x) trzyma się prawdy.

Utwórz plik skryptu i wpisz w nim następujący kod -

syms x
y = 3*sin(x)+7*cos(5*x);  % defining the function
lhs = diff(y,2)+y;        %evaluting the lhs of the equation
rhs = -5*cos(2*x);        %rhs of the equation
if(isequal(lhs,rhs))
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Po uruchomieniu pliku wyświetla następujący wynik -

No, the equation does not hold true
Value of LHS is: 
-168*cos(5*x)

Poniżej znajduje się odpowiednik oktawowy powyższego obliczenia -

pkg load symbolic
symbols

x = sym("x");
y = 3*Sin(x)+7*Cos(5*x);           % defining the function
lhs = differentiate(y, x, 2) + y;  %evaluting the lhs of the equation
rhs = -5*Cos(2*x);                 %rhs of the equation

if(lhs == rhs)
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Octave wykonuje kod i zwraca następujący wynik -

No, the equation does not hold true
Value of LHS is: 
-(168.0)*cos((5.0)*x)

Znajdowanie maksimów i minimów krzywej

Jeśli szukamy lokalnych maksimów i minimów dla wykresu, w zasadzie szukamy najwyższych lub najniższych punktów na wykresie funkcji w określonej miejscowości lub określonego zakresu wartości zmiennej symbolicznej.

Dla funkcji y = f (x) nazywane są punkty na wykresie, w których wykres ma zerowe nachylenie stationary points. Innymi słowy, punkty stacjonarne to gdzie f '(x) = 0.

Aby znaleźć stacjonarne punkty funkcji, którą rozróżniamy, musimy ustawić pochodną równą zero i rozwiązać równanie.

Przykład

Znajdźmy punkty stacjonarne funkcji f (x) = 2x ³ + 3x ² - 12x + 17

Wykonaj następujące kroki -

First let us enter the function and plot its graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y)

MATLAB wykonuje kod i zwraca następujący wykres -

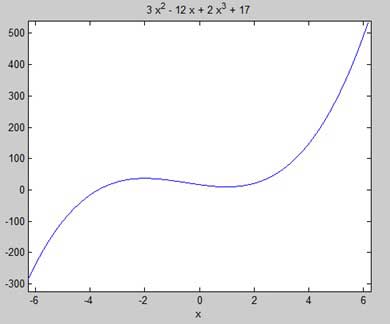
Here is Octave equivalent code for the above example −

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y)
print -deps graph.eps

Our aim is to find some local maxima and minima on the graph, so let us find the local maxima and minima for the interval [-2, 2] on the graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y, [-2, 2])

MATLAB executes the code and returns the following plot −

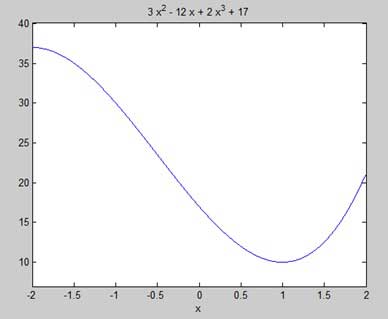
Here is Octave equivalent code for the above example −

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y, [-2, 2])
print -deps graph.eps

Next, let us compute the derivative.

g = diff(y)

MATLAB executes the code and returns the following result −

g =
   6*x^2 + 6*x - 12

Here is Octave equivalent of the above calculation −

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

Octave executes the code and returns the following result −

g =
   -12.0+(6.0)*x+(6.0)*x^(2.0)

Let us solve the derivative function, g, to get the values where it becomes zero.

s = solve(g)

MATLAB executes the code and returns the following result −

s =
   1
   -2

Following is Octave equivalent of the above calculation −

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])

Octave executes the code and returns the following result −

g =

-12.0+(6.0)*x^(2.0)+(6.0)*x
ans =

  -2
   1

This agrees with our plot. So let us evaluate the function f at the critical points x = 1, -2. We can substitute a value in a symbolic function by using the subs command.

subs(y, 1), subs(y, -2)

MATLAB executes the code and returns the following result −

ans =
   10
ans =
   37

Following is Octave equivalent of the above calculation −

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)

ans =
   10.0
ans =
   37.0-4.6734207789940138748E-18*I

Therefore, The minimum and maximum values on the function f(x) = 2x³ + 3x² − 12x + 17, in the interval [-2,2] are 10 and 37.

Solving Differential Equations

MATLAB provides the dsolve command for solving differential equations symbolically.

The most basic form of the dsolve command for finding the solution to a single equation is

dsolve('eqn')

where eqn is a text string used to enter the equation.

It returns a symbolic solution with a set of arbitrary constants that MATLAB labels C1, C2, and so on.

You can also specify initial and boundary conditions for the problem, as comma-delimited list following the equation as −

dsolve('eqn','cond1', 'cond2',…)

For the purpose of using dsolve command, derivatives are indicated with a D. For example, an equation like f'(t) = -2*f + cost(t) is entered as −

'Df = -2*f + cos(t)'

Higher derivatives are indicated by following D by the order of the derivative.

For example the equation f"(x) + 2f'(x) = 5sin3x should be entered as −

'D2y + 2Dy = 5*sin(3*x)'

Let us take up a simple example of a first order differential equation: y' = 5y.

s = dsolve('Dy = 5*y')

MATLAB executes the code and returns the following result −

s =
   C2*exp(5*t)

Let us take up another example of a second order differential equation as: y" - y = 0, y(0) = -1, y'(0) = 2.

dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')

MATLAB executes the code and returns the following result −

ans =
   exp(t)/2 - (3*exp(-t))/2