MATLAB - Operatory

Operator to symbol, który mówi kompilatorowi, aby wykonał określone operacje matematyczne lub logiczne. MATLAB został zaprojektowany do działania przede wszystkim na całych macierzach i tablicach. Dlatego operatory w MATLAB-ie działają zarówno na danych skalarnych, jak i nieskalarnych. MATLAB pozwala na następujące typy podstawowych operacji -

Operatory arytmetyczne
Operatorzy relacyjni
Operatory logiczne
Operacje bitowe
Operacje na zbiorach

Operatory arytmetyczne

MATLAB pozwala na dwa różne rodzaje operacji arytmetycznych -

Operacje arytmetyczne na macierzach
Operacje arytmetyczne na tablicach

Operacje arytmetyczne na macierzach są takie same, jak w algebrze liniowej. Operacje na tablicach są wykonywane element po elemencie, zarówno na jednowymiarowej, jak i wielowymiarowej tablicy.

Operatory macierzy i operatory tablicowe są rozróżniane za pomocą symbolu kropki (.). Jednak ponieważ operacje dodawania i odejmowania są takie same dla macierzy i tablic, operator jest taki sam w obu przypadkach. Poniższa tabela zawiera krótki opis operatorów -

Pokaż przykłady

Sr.No.	Operator i opis
1	+ Dodatek lub jednoargumentowy plus. A + B dodaje wartości przechowywane w zmiennych A i B. A i B muszą mieć ten sam rozmiar, chyba że jeden jest skalarem. Do macierzy o dowolnej wielkości można dodać skalar.
2	- Odejmowanie lub jednoargumentowy minus. AB odejmuje wartość B od A. A i B muszą mieć ten sam rozmiar, chyba że jeden jest skalarem. Z macierzy o dowolnej wielkości można odjąć skalar.
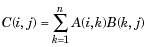
3	* Mnożenie macierzy. C = A * B jest liniowym iloczynem algebraicznym macierzy A i B. Dokładniej, W przypadku nieskalarnych A i B liczba kolumn A musi być równa liczbie wierszy B. Skalar może pomnożyć macierz dowolnego rozmiaru.
4	.* Mnożenie tablicy. A. * B jest iloczynem element po elemencie tablic A i B. A i B muszą mieć ten sam rozmiar, chyba że jeden z nich jest skalarem.
5	/ Ukośnik lub prawy podział macierzy. B / A jest mniej więcej tym samym, co B * inv (A). Dokładniej, B / A = (A '\ B') '.
6	./ Prawidłowy podział tablicy. A./B to macierz z elementami A (i, j) / B (i, j). A i B muszą mieć ten sam rozmiar, chyba że jeden z nich jest skalarem.
7	\ Ukośnik odwrotny lub podział macierzy z lewej strony. Jeśli A jest macierzą kwadratową, A \ B jest mniej więcej tym samym, co inv (A) * B, z wyjątkiem tego, że jest obliczane w inny sposób. Jeżeli A oznacza grupę n-o-N matrycy i B jest wektorem kolumny z elementami N lub matryca z kilku takich kolumn, a X = A \ B jest rozwiązaniem równania AX = B . Komunikat ostrzegawczy jest wyświetlany, jeśli A jest źle wyskalowane lub prawie pojedyncze.
8	.\ Lewy podział tablicy. A. \ B to macierz z elementami B (i, j) / A (i, j). A i B muszą mieć ten sam rozmiar, chyba że jeden z nich jest skalarem.
9	^ Moc matrycy. X ^ p jest X do potęgi p, jeśli p jest skalarem. Jeśli p jest liczbą całkowitą, moc obliczana jest przez powtórne podniesienie do kwadratu. Jeśli liczba całkowita jest ujemna, X jest odwracany jako pierwszy. W przypadku innych wartości p obliczenie obejmuje wartości własne i wektory własne, tak że jeśli [V, D] = eig (X), to X ^ p = V * D. ^ p / V.
10	.^ Moc tablicowa. A. ^ B to macierz z elementami A (i, j) do potęgi B (i, j). A i B muszą mieć ten sam rozmiar, chyba że jeden z nich jest skalarem.
11	' Macierz transponowana. A 'jest liniową algebraiczną transpozycją A. W przypadku macierzy zespolonych jest to transpozycja sprzężona zespolona.
12	.' Tablica transponowana. ZA.' jest tablicą transpozycji A. W przypadku złożonych macierzy nie obejmuje to koniugacji.

Operatorzy relacyjni

Operatory relacyjne mogą również pracować na danych skalarnych i nieskalarnych. Operatory relacyjne dla tablic wykonują porównania element po elemencie między dwiema tablicami i zwracają tablicę logiczną o tym samym rozmiarze, z elementami ustawionymi na logiczne 1 (prawda), gdzie relacja jest prawdziwa, a elementy ustawione na logiczne 0 (fałsz), gdzie jest nie.

Poniższa tabela przedstawia operatory relacyjne dostępne w MATLAB -

Pokaż przykłady

Sr.No.	Operator i opis
1	< Mniej niż
2	<= Mniejszy lub równy
3	> Lepszy niż
4	>= Większe bądź równe
5	== Równy
6	~= Nie równa się

Operatory logiczne

MATLAB oferuje dwa typy operatorów logicznych i funkcji -

Pod względem elementów - operatory te działają na odpowiednich elementach tablic logicznych.
Zwarcie - te operatory działają na wyrażeniach skalarnych i logicznych.

Operatory logiczne oparte na elementach operują element po elemencie na tablicach logicznych. Symbole &, | i ~ to logiczne operatory tablicowe AND, OR i NOT.

Operatory logiczne zwarcia umożliwiają zwarcie w operacjach logicznych. Symbole && i || są logicznymi operatorami zwarć AND i OR.

Pokaż przykłady

Operacje bitowe

Operatory bitowe pracują na bitach i wykonują operacje bit po bicie. Tabele prawdy dla &, | i ^ są następujące -

p	q	p & q	p \| q	p ^ q
0	0	0	0	0
0	1	0	1	1
1	1	1	1	0
1	0	0	1	1

Załóżmy, że A = 60; i B = 13; Teraz w formacie binarnym będą one następujące -

A = 0011 1100

B = 0000 1101

-----------------

A&B = 0000 1100

A | B = 0011 1101

A ^ B = 0011 0001

~ A = 1100 0011

MATLAB zapewnia różne funkcje dla operacji bitowych, takich jak operacje „bitowe i”, „bitowe lub” i „nie bitowe”, operacje przesunięcia itp.

W poniższej tabeli przedstawiono najczęściej używane operacje bitowe -

Pokaż przykłady

Funkcjonować	Cel, powód
bitand (a, b)	Bit-mądry AND liczb całkowitych a i b
bitcmp (a)	Pod względem bitowym uzupełnienie pliku
bitget (a, pos)	Pobierz bit w określonej pozycji pos , w tablicy liczb całkowitych a
bitor (a, b)	Bit-mądry OR liczb całkowitych a i b
zestaw bitów (a, pos)	Ustawiony bit na określonej lokalizacji poz od A
przesunięcie bitowe (a, k)	Zwraca przesunął się w lewo przez k bitów, co odpowiada mnożenie przez 2 ^k . Ujemne wartości k odpowiadają przesunięciu bitów w prawo lub podzieleniu przez 2 ^{\| k \|}i zaokrąglenie do najbliższej liczby całkowitej w kierunku ujemnej nieskończoności. Wszelkie bity przepełnienia są obcinane.
bitxor (a, b)	Bit-mądry XOR liczb całkowitych a i b
swapbytes	Zamień kolejność bajtów

Operacje na zbiorach

MATLAB zapewnia różne funkcje dla operacji na zbiorach, takie jak sumowanie, przecinanie i testowanie członkostwa w zestawie itp.

W poniższej tabeli przedstawiono niektóre często używane operacje na zbiorach -

Pokaż przykłady

Sr.No.	Opis funkcji
1	intersect(A,B) Ustaw przecięcie dwóch tablic; zwraca wartości wspólne zarówno dla A, jak i B. Zwracane wartości są posortowane.
2	intersect(A,B,'rows') Traktuje każdy wiersz A i każdy wiersz B jako pojedyncze jednostki i zwraca wiersze wspólne dla obu A i B. Wiersze zwróconej macierzy są posortowane.
3	ismember(A,B) Zwraca tablicę tego samego rozmiaru co A, zawierającą 1 (prawda), gdzie elementy A znajdują się w B. W innym przypadku zwraca 0 (fałsz).
4	ismember(A,B,'rows') Traktuje każdy wiersz A i każdy wiersz B jako pojedyncze jednostki i zwraca wektor zawierający 1 (prawda), gdzie wiersze macierzy A są również wierszami B. W innym przypadku zwraca 0 (fałsz).
5	issorted(A) Zwraca logiczne 1 (prawda), jeśli elementy A są posortowane, a logiczne 0 (fałsz) w przeciwnym razie. Wejście A może być wektorem lub tablicą łańcuchów komórek N na 1 lub 1 na N.A is considered to be sorted if A a wyniki sortowania (A) są równe.
6	issorted(A, 'rows') Zwraca logiczną 1 (prawda), jeśli wiersze dwuwymiarowej macierzy A są posortowane, a logiczne 0 (fałsz) w przeciwnym razie. Matrix A is considered to be sorted if A a wyniki sortowania (A) są równe.
7	setdiff(A,B) Ustawia różnicę dwóch tablic; zwraca wartości w A, których nie ma w B. Wartości w zwróconej tablicy są posortowane.
8	setdiff(A,B,'rows') Traktuje każdy wiersz A i każdy wiersz B jako pojedyncze jednostki i zwraca wiersze z A, których nie ma w B. Wiersze zwróconej macierzy są posortowane. Opcja „wiersze” nie obsługuje tablic komórek.
9	setxor Ustawia wyłączne LUB dwóch tablic
10	union Ustawia sumę dwóch tablic
11	unique Unikalne wartości w tablicy